多載波OFDM信號識別方法

朱立為, 黃知濤

(國防科技大學電子科學學院, 湖南 長沙 410073)

0 引 言

近些年來,由于無人機的大量使用,無人機非法入侵事件時有發生,催生了以無人機為目標的對抗技術研究。而在通信無源對抗領域中,針對無人機測控數傳信號的盲處理技術研究也成為一個十分重要的課題,而無人機測控數傳信號采用的便是正交頻分復用(orthogonal frequency division multiplexing, OFDM)信號。OFDM信號的盲處理技術研究,包括信號的檢測識別、參數估計、解調及測角定位等技術問題。由于OFDM信號采用頻分多路復用(frequency division multiplexing,FDM)技術,適用于高數據速率的無線傳輸,其非合作處理技術也與單載波調制信號略有不同。因此,首先要解決OFDM信號的識別問題。

因為OFDM信號在時域上有類高斯特性,所以許多文獻中提出用高階矩或者高階累積量來識別多載波與單載波信號。早期,文獻[1]中用二階矩與高階矩及高階矩之間的比值聯合來識別,當信噪比(signal to noise ratio, SNR)大于5 dB時,識別率大于90%,識別依賴一確定閾值,只能用于其特定環境條件下。文獻[2]中通過計算分析不同子載波調制的OFDM信號四階累積量的值分布與一般單載波信號的分布情況,設定合適的經驗門限來區分單載波調制信號與OFDM信號,該方法受頻率影響大。文獻[3]基于參數極大似然函數的識別方法,需要提前估計SNR。文獻[4-5]中基于多尺度小波分解后的特征向量的支持向量機(support vector machine, SVM)分類方法,此方法無法避免小波分解層數的選擇及運量大的問題。近來隨著大數據深度學習研究的興起,采用深度學習的方法來實現OFDM信號識別也屢見不鮮,如文獻[6-7],但深度學習方法比較依賴訓練數據的質量,且對信號環境的范化能力也有待提高。

實際上在無人機測控信號非合作處理環境中,不但要考慮區分OFDM信號與單載波信號,還要考慮OFDM信號與其他多載波信號之間的區分,如頻分多址(frequency division multiple access, FDMA)信號、跳頻(frequency hopping, FH)通信信號、多載波時分多址(multi frequency time division multiple access, MF-TDMA)信號等,存在信號處理環境極為復雜、信道選擇性衰落、多普勒以及多徑等問題。

本文提出了基于包絡相關譜的OFDM識別算法,該方法既利用了OFDM信號的循環前綴的特征,又利用其類高斯性。通過計算OFDM信號包絡相關譜，在變換域中實現OFDM信號的識別。該方法并不需要任何信號先驗信息,同時還能估計出OFDM信號的子載波符號速率。

1 信號模型

1.1 單載波信號模型

在加性信道噪聲條件下,單載波傳輸系統中,接收的數字基帶信號的一般數學表達式為

()=()+()

(1)

(2)

式中:()為加性噪聲;()為脈沖成型形狀;為第個碼元所對應的電平值,為碼元持續時間。

1.2 OFDM多載波信號模型

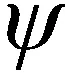
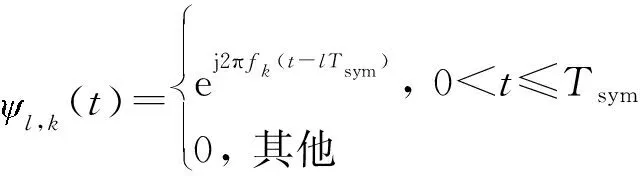
(3)

得到基帶時間連續的OFDM信號表達式如下:

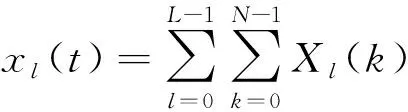
(4)

對式(4) OFDM基帶信號進行采樣,令=+,=,=,可以得到OFDM符號的離散時間表達式如下:

(5)

易得基帶OFDM接收符號表達式為

(6)

考慮信道的帶限情況,則有()=,(-)，其中,(-)為信號脈沖形狀。

因此,在加性高斯白噪聲條件下的多載波OFDM信號接收模型表達式如下:

()=()+()

(7)

2 包絡相關譜

2.1 單載波信號包絡相關譜

由文獻[9]可知,數字調制信號的包絡傅里葉變換(本文中定義為包絡譜)在符號速率處存在離散譜線,可以用來估計信號的碼速率。

利用式(1)，假設信號為復信號,則信號的包絡為|()|,有如下推導過程:

(8)

所以其包絡平方|()|=|()|+|()|,由于復包絡絕對值的傅里葉變換進行推導比較復雜,對復包絡平方的傅里葉變換進行了理論推導,易知：

(9)

設()的傅里葉變換為(),根據傅里葉變換的基本性質中的頻域卷積性質,可得()的傅里葉變換為(12π)()*()(*表示卷積),因此得到其完整包絡譜為

(10)

而在通信過程中,信號都是帶寬受限的,即當||>2π時,有()=0,于是在頻率=±2π處出現了離散譜線。

同理,可以推導包絡相關譜過程:

()=E{|()‖(-)|}=E{|()+()‖(-)+(-)|}

(11)

式中：E(·)表示求均值。

其中，設接收信號的采樣長度為,使得和取值滿足以下條件:

(12)

由于()與()不相關,且加性高斯白噪聲非相關性可知E{|()(-)|}≈0,可得單載波信號的包絡譜相關波形:

()=E{|()(-)|+|()(-)|}=E{|()(-)|}

(13)

根據傅里葉變換的基本性質中的相關性質，可以得單載波信號完整的包絡相關譜:

()=F[E{}]=F[E{|()(-)|}]=

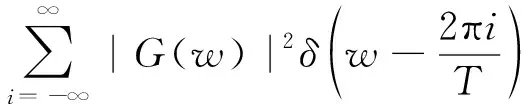
(14)

同理可得,在頻率=±2π處會有離散的包絡相關譜線。

綜上可以看出,包絡相關譜與包絡譜相比,具有一定的噪聲抑制能力。

2.2 多載波OFDM信號的包絡相關譜

前面已經推導介紹了單載波信號的包絡相關譜,很顯然,包絡相關譜具有抑制加性高斯白噪聲的作用，可以作信號的符號速率。下面推導多載波OFDM信號的包絡相關譜。

OFDM信號表達式如下:

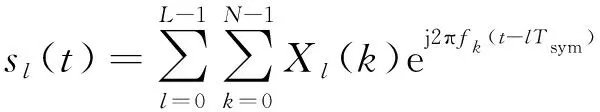
(15)

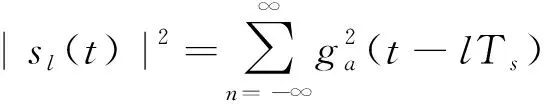
(16)

(17)

而在通信過程中,信號都是帶寬受限的,對于OFDM信號，其帶寬為,為子載波總數據,即當||>2π時,有()=0,于是在頻率=±2π,≤處出現了離散譜線，且具有頻域周期性。

同理,可以推導包絡相關譜過程：

()=E{|()‖(-)|}=E{|()+()‖(-)+(-)|}

(18)

其中，設接收信號的采樣長度為,使得和取值滿足以下條件:

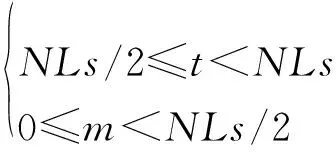
(19)

由()與()不相關,且加性高斯白噪聲非相關性可知E{|()(-)|}≈0,可得單載波信號的包絡譜相關波形:

()=E{|()(-)|+|()(-)|}=E{|()(-)|}

(20)

根據傅里葉變換的基本性質中的相關性質可以得多載波OFDM信號完整的包絡相關譜：

()=F[E{}]=F[E{|()(-)|}]=

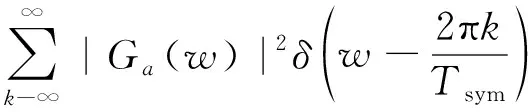
(21)

綜上可以看出,在頻率=±2π,≤處會有離散的包絡相關譜線,且譜線具有等間隔周期性,后續可作為區分多載波OFDM信號與單載波信號的有效依據。同時,對多載波OFDM信號,包絡相關譜的一些性能仍然存在,即與包絡譜相比,具有一定的噪聲抑制能力。

通過第2節對單載波信號和多載波OFDM的包絡相關譜的推導可知:

(1) 通信信號帶限條件下,單載波信號的復包絡相關譜只在正負符號速率的頻率位置出現離散的譜線;

(2) 多載波OFDM信號在帶限條件下,由于其具有多子載波特性,其復包絡相關譜的離散譜線會出現在正負子載波符號速率1至倍的頻率位置,且具有周期性,其中為子載波數;

(3) 包絡相關譜相比包絡譜具有更好的高斯白噪聲抑制能力。

因此,本文識別OFDM信號的策略是通過計算信號的包絡相關譜,然后檢測其離散譜線,判斷其周期性來區分是OFDM信號還是單載波信號。

3 仿真分析

3.1 識別率

為了驗證包絡相關譜對OFDM信號的識別性能,本文仿真時采用正確識別率作為指標,來衡量OFDM信號的識別性能,定義識別正確率RMP=MC×100%。其中,表示正確識別的次數,MC為蒙特卡羅重復試驗次數,RMP為正確識別概率的試驗估計值。

3.2 仿真實驗

單載波常規信號包絡譜與包絡相關譜仿真分析

在本仿真分析中,設接收機采樣率=56 MHz,信號中頻頻率=70 MHz,符號速率Rs=2 500 kHz,信號采樣點數Len=1 048 576,加入SNR為3 dB的高斯白噪聲,脈沖成形()采用平方根升余弦,滾降系數=05,調制樣式分別為二階相移鍵控(binary phase shift keying, BPSK)、四階相移鍵控(quadrature phase shift keying，QPSK)、16階正交幅度調制(sixteen quadrature amplitude modulation, 16QAM)，產生信號并計算其包絡譜和包絡相關譜,仿真結果如圖1所示。

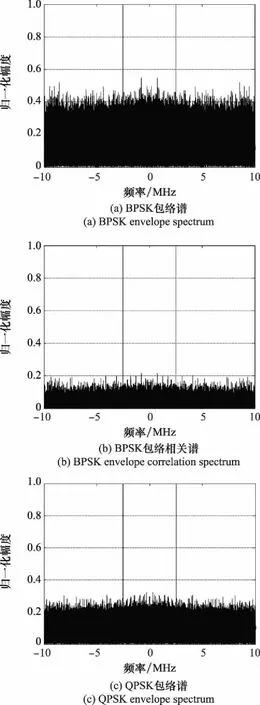
圖1 單載波常規信號包絡譜與包絡相關譜Fig.1 Envelope spectrum and envelope correlation spectrum of single-carrier normal signal

從圖1可以發現,對于單載波常規信號,其包絡相關譜相比包絡譜具有抑制高斯白噪聲的作用,而且包絡相關譜與包絡譜一樣,在符號速率頻率位置也具有離散的譜線,能夠用來估計信號的符號速率。

單載波擴頻信號包絡譜與包絡相關譜仿真分析

在本仿真分析中,設接收機采樣率=56 MHz,信號中頻頻率=70 MHz,符號速率Rs=2 500 kHz,信號采樣點數Len=1 048 576,加入SNR=3 dB的高斯白噪聲,脈沖成形()采用平方根升余弦,滾降系數=0.5,調制樣式分別為BPSK;擴頻碼類型為序列,擴頻碼階數為9,碼長為511,產生直接序列擴頻(direct sequence spread spectrum, DSSS)信號并計算其包絡譜和包絡相關譜,仿真結果如圖2所示。

3)然后根據判斷矩陣的一致性程度與Step2中的聚類分析權重相結合(乘積關系)，求解綜合的專家權重，然后對專家權重進行歸一化處理。

圖2 DSSS信號包絡譜與包絡相關譜Fig.2 Envelope spectrum and envelope correlation spectrum of DSSS signal

從圖2可以發現,對于擴頻信號,包絡相關譜仍然具有高斯白噪聲抑制能力。

多載波FDMA信號包絡譜與包絡相關譜仿真分析

在本仿真分析中,設接收機采樣率=56 MHz,接收機中頻頻率=70 MHz,子帶符號速率Rs=200 kHz,信號采樣點數Len=1 048 576,加入SNR=3 dB的高斯白噪聲,脈沖成形()采用平方根升余弦,滾降系數=0.5,調制樣式分別為BPSK;用戶數為20,用戶之間頻率間隔為450 kHz,產生信號并計算其包絡譜和包絡相關譜,仿真結果如圖3和圖4所示。

圖3 多載波FDMA信號頻譜Fig.3 Spectrum of multi-carrier FDMA signal

圖4 多載波FDMA信號包絡譜與包絡相關譜Fig.4 Envelope spectrum and envelope correlation spectrum of multi-carrier FDMA signal

從圖3可以看出,對于多載波FDMA信號的頻譜具有多子帶特征,與多載波OFDM信號頻譜有些相似。

從圖4可以看出,對于多載波FDMA信號,其包絡相關譜與單載波信號接近,與多載波OFDM信號區別明顯,同時也具有高斯白噪聲抑制能力。

多載波OFDM信號包絡譜與包絡相關譜仿真分析

在本仿真分析中,設接收機采樣率=56 MHz,接收機中頻頻率=70 MHz,符號速率Rs=1 000 kHz,信號采樣點數Len=1 048 576,加入SNR=3 dB的高斯白噪聲;子載波個數為64,數據子載波數為48,碼片時長為0.05 μs,子載波脈沖成形()采用平方根升余弦,滾降系數=0.5,子載波調制樣式分別為QPSK,產生信號并計算其包絡譜和包絡相關譜,仿真結果如圖5和圖6所示。

圖5 多載波OFDM頻譜Fig.5 Spectrum of multi-carrier OFDM

圖6 多載波OFDM包絡譜與包絡相關譜Fig.6 Envelope spectrum and envelope correlation spectrum of multi-carrier OFDM

從圖5可以看出,對于多載波OFDM信號的頻譜具有多子帶特征,與多載波FDMA信號頻譜有些相似。

從圖6可以發現,對于多載波OFDM信號,其包絡相關譜與多載波FDMA區別明顯,同時相比包絡譜具有抑制高斯白噪聲的作用,而且包絡相關譜與包絡譜一樣,在子載波的符號速率頻率位置也具有離散的譜線,能夠用來估計子載波的符號速率。

識別率對比仿真分析

在本仿真分析中,設接收機采樣率=56 MHz,接收機中頻頻率=70 MHz,符號速率Rs=1 000 kHz,信號采樣點數Len=1 048 576,加入的高斯白噪聲SNR變化范圍為-10～10 dB;子載波個數為64,數據子載波數為48,碼片時長為0.05 μs,子載波脈沖成形()采用平方根升余弦,滾降系數=0.5,子載波調制樣式分別為QPSK,產生多載波OFDM中頻采樣信號。

用本文基于包絡相關譜的方法與基于包絡譜、高階累積量的識別方法分別對OFDM信號進行識別,計算其識別正確率RMP,進行500次蒙特卡羅試驗,結果如圖7所示。

圖7 識別率隨SNR的變化情況Fig.7 Variation of recognition rate with SNR

從圖7可以看出,本文算法在SNR為-9 dB時,識別正確率可以達到90%,比基于包絡譜的方法提升了3 dB;本文算法在SNR為-5 dB時,識別正確率可以達到100%,而高階累積量的方法在0 dB時,才能達到100%;同時,對低SNR環境的適應能力要優于基于高階累積量的方法6 dB左右。

另外,在多次識別實驗時,統計了3種識別算法的平均識別時間,結果如圖8所示。

圖8 平均識別時間隨SNR的變化情況Fig.8 Variation of average time-consuming with SNR

從圖8可看出,本文算法在時間復雜度上會有一定的上升,這是因為增加了相關運算,但時效性還是與基于包絡特征的識別方法處于一個數量級上。

4 結 論

針對多載波OFDM信號的識別問題,本文提出了一種基于包絡相關譜的識別算法。該方法通過檢測信號包絡相關譜的周期性離散譜線,實現多載波OFDM信號與單載波常規信號及多載FDMA信號的區分,從而完成對OFDM信號的識別。

本文提出的識別算法,由于使用了信號包絡相關譜,相比包絡譜具有噪聲抑制能力,提高了算法在低SNR條件下的識別估計能力。其次,包絡相關譜的周期特征不受信號頻率影響,相比高階累積量的識別方法,具體更好的低SNR環境適應能力。仿真結果表明,本文算法的多載波OFDM信號識別性能優于高階累積量的算法。同時,還能估計OFDM信號的子載波符號速率。