磁致伸縮效應(yīng)對永磁同步電機(jī)振動噪聲影響分析*

羅 進(jìn),于慎波,竇汝桐,翟鳳晨

(沈陽工業(yè)大學(xué) 機(jī)械工程學(xué)院，遼寧 沈陽 110870)

0 引言

電機(jī)的振動噪聲是電機(jī)研究中的主要問題之一,但人們常常忽略鐵心磁致伸縮效應(yīng)的影響[1，2]，近些年來國內(nèi)外學(xué)者逐漸重視鐵心磁致伸縮效應(yīng)對電機(jī)振動噪聲影響的研究。美國學(xué)者M(jìn)ohammed O A等[3，4]提出了一個考慮磁致伸縮效應(yīng)的電磁、機(jī)械力以及相關(guān)材料的數(shù)值模型，發(fā)現(xiàn)鐵心磁致伸縮效應(yīng)也會引起定子形變，在計算時發(fā)現(xiàn)鐵心磁致伸縮效應(yīng)對一臺2馬力電機(jī)的影響達(dá)到了50%。英國帝國理工大學(xué)博士Belahcen Anouar[5]分別計算了一臺同步電機(jī)和一臺異步電機(jī)定子鐵心的振動，發(fā)現(xiàn)在某些頻率鐵心磁致伸縮效應(yīng)會加劇定子鐵心振動，而在另外一些頻率會使其減小。沈陽工業(yè)大學(xué)的韓雪巖等[6]利用有限元法對有鐵心磁致伸縮效應(yīng)的電機(jī)伸縮進(jìn)行數(shù)值計算，分析了電機(jī)的振動噪聲。河北工業(yè)大學(xué)的閆榮格等[7]對實際工況下考慮電磁力和磁致伸縮效應(yīng)的感應(yīng)電機(jī)的應(yīng)力和振動進(jìn)行計算，并分析了諧波對電機(jī)振動的影響。本文對永磁同步電機(jī)進(jìn)行建模和仿真分析，以確定鐵心磁致伸縮效應(yīng)對永磁同步電機(jī)振動噪聲的影響。

1 電機(jī)的機(jī)電耦合數(shù)學(xué)模型

根據(jù)麥克斯韋方程和材料的各向異性的描述，得到激勵電流z方向分量Je的偏微分方程：

(1)

其中：vxx、vxy、vyx、vyy為平面內(nèi)不同方向的磁阻率對單元應(yīng)力的變化率；σxx、σxy、σyx、σyy為應(yīng)力張量在不同方向的值；A為磁矢勢。

電機(jī)系統(tǒng)的總能量泛函Et可以用式(2)來表示，該系統(tǒng)包括磁場能、電流位能、機(jī)械能和外力做功大小。

(2)

其中：R為磁場域；B為磁通密度；H為磁場強(qiáng)度；V為機(jī)械域的體積；ε、σ為應(yīng)變張量和應(yīng)力張量;fV為外部體積力密度；τ為機(jī)械域邊界;fτ為外部表面力密度；U為振動位移。

將機(jī)械系統(tǒng)總能量分別對振動位移和磁矢勢求偏導(dǎo)，可得到機(jī)械場和磁場的能量泛函駐點如式(3)、式(4)所示：

(3)

(4)

其中：Etm為機(jī)械場總能量；Ete為磁場的總能量；Ui和Ai分別為機(jī)械場和磁場在節(jié)點i處的位移和磁矢勢。

根據(jù)虛功原理，通過保持兩個節(jié)點之間磁矢勢之差不變，則沿位移方向的電磁作用力等于磁能相對位移的變化。每個單元電磁力可以表示為：

(5)

其中：Re為單元電磁場的面積；G為雅可比微分矩陣。

式(5)中第三項相當(dāng)于磁致伸縮力的分量，而且在式(5)中可以得到：

(6)

其中：E為材料的彈性模量；v為泊松比。所以磁致伸縮單元力可以用式(7)表示：

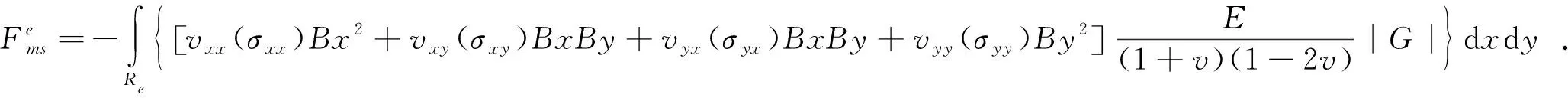
(7)

可以得到如下用來表示電磁場和機(jī)械場耦合問題的矩陣：

[S][A]=[Je].

(8)

[K][U]=[F].

(9)

其中：[S]為電磁剛度矩陣；[A]為磁矢量矩陣；[Je]為激勵電流密度矩陣；[K]為機(jī)械剛度矩陣；[U]為振動位移矩陣；[F]為施加在應(yīng)力場中的力，包括電磁力和磁致伸縮力。

2 電機(jī)電磁場仿真分析

本文以一臺9.5 kW8級36槽的永磁同步電機(jī)為研究對象，利用Maxwell建立的電機(jī)二維有限元仿真模型如圖1所示。電機(jī)在工作過程中的主要參數(shù)如表1所示。本文電機(jī)硅鋼片的磁致伸縮特性曲線如圖2所示。將曲線數(shù)值添加到硅鋼片的材料屬性中，計算有磁致伸縮效應(yīng)時的徑向電磁力。

圖1 電機(jī)有限元計算模型

表1 電機(jī)主要參數(shù)

圖2 電機(jī)硅鋼片的磁致伸縮特性曲線

圖3為有磁致伸縮效應(yīng)和無磁致伸縮效應(yīng)時的徑向電磁力與諧波分析對比，取半個電周期結(jié)果進(jìn)行觀察。從圖3(a)中可以看出，在數(shù)值上有磁致伸縮效應(yīng)的電磁力總體比無磁致伸縮效應(yīng)的大。從圖3(b)中可以看出,電磁力低次諧波的幅值較大，可能會引起較大的振動，但當(dāng)電磁力特定階次激振力波頻率與電機(jī)固有頻率接近時，力波的幅值較小也會發(fā)生共振。

圖3 有、無磁致伸縮效應(yīng)時的徑向電磁力與諧波分析對比

3 電機(jī)模態(tài)與諧響應(yīng)仿真分析

利用ANSYS Workbench建立電機(jī)的三維模型，已知電機(jī)材料，其泊松比為0.28，彈性模量為196 GPa，密度為7 700 kg/m3。利用模態(tài)計算模塊進(jìn)行分析，得到的電機(jī)前6階模態(tài)固有頻率如表2所示。

表2 電機(jī)前6階模態(tài)固有頻率

圖4為有、無磁致伸縮效應(yīng)電機(jī)機(jī)殼表面的加速度頻譜對比圖。為了方便觀察，將振動加速度取對數(shù)即為振動加速度級。由圖4可以看出，振動加速度最大的頻段在6 400 Hz，之后下降。原因是此頻段接近第6階模態(tài)的固有頻率。電機(jī)第6階模態(tài)的振型如圖 5所示。

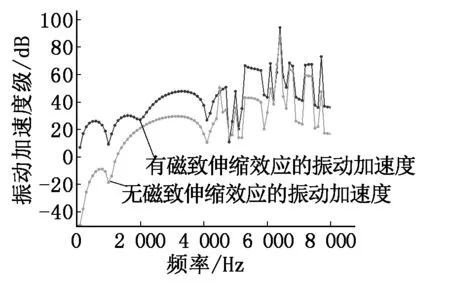
圖4 有、無磁致伸縮效應(yīng)時電機(jī)機(jī)殼表面加速度級

4 電機(jī)噪聲仿真分析

在電機(jī)外建立半徑1.5 m的空氣包作為聲場響應(yīng)計算區(qū)域，得出有、無磁致伸縮效應(yīng)時機(jī)殼表面的聲壓級曲線，如圖6所示，發(fā)現(xiàn)有磁致伸縮效應(yīng)時的噪聲在大部分情況下大于無磁致伸縮效應(yīng)的。

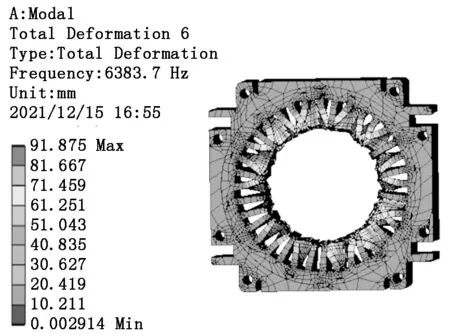
圖5 電機(jī)第6階模態(tài)振型

圖6 有、無磁致伸縮效應(yīng)時機(jī)殼表面的聲壓級曲線

5 結(jié)論

本文分別建立了永磁同步電機(jī)的二維和三維有限元模型，并進(jìn)行電磁場計算、模態(tài)和固有頻率分析、振動噪聲分析。對有無磁致伸縮效應(yīng)的徑向電磁力、振動加速度和噪聲進(jìn)行分析，可以得到有磁致伸縮效應(yīng)的各項結(jié)果均比無磁致伸縮效應(yīng)的大，研究結(jié)果對電機(jī)的減振降噪以及設(shè)計制造有一定的指導(dǎo)意義。