基于k-shape算法的行業(yè)典型負荷特征研究

國網(wǎng)四川省營銷服務中心 王良之 姚岱州 馬浩原

1 引言

2020年迎峰度冬受寒潮和電煤供應短缺的影響，電力供需形勢嚴峻。開展重點行業(yè)典型負荷特征研究，為提升電力市場分析預測、實施需求側響應，以及準確把握負荷供需形勢奠定技術基礎。文獻[1]利用反映負荷特征的向量，通過聚類方式對負荷開展分類，提升了短期負荷預測準確率。另外，掌握行業(yè)負荷特征，也將有利于開展對重要工業(yè)客戶的用能結構和成本分析，為進一步做好綜合能源服務和開展電力市場交易奠定基礎，成為經(jīng)營效益的重要抓手。

電力負荷曲線的特征研究中，往往以曲線聚類為研究起點，目前常用的電力負荷曲線聚類的方法有k 均值聚類、層次聚類、模糊C 均值聚類、動態(tài)時間彎曲距離（DTW），以及以此為基礎改進的算法，這些算法多以歐式距離作為相似性判距的方式，難以識別曲線形態(tài)。因此，刻畫曲線形態(tài)成為聚類的關鍵。另外，使用傳統(tǒng)聚類方法對96點負荷數(shù)據(jù)進行聚類，計算量大，分類效果未必有很大的提升。

電力負荷曲線采集頻率精細化，有利于負荷分析，然而也帶來了高維數(shù)據(jù)計算量大的問題。負荷曲線96點采集頻次，雖然對于區(qū)分刻畫負荷曲線的差異有幫助，也同樣增加了噪聲因素，給聚類分析帶來不便，影響分析結果。因此，如何對負荷曲線提取有效特征，成為分析負荷的關鍵核心，而如何開展對負荷曲線特征的分類，正是聚類分析所研究的命題。因此，有效提取特征，也成為聚類分析的起點[2]。

本文基于k-shape 的聚類算法，對負荷序列進行聚類，此算法提出基于時間序列形態(tài)相似性的距離度量方式，并采用一種新的聚類中心計算方式提取每類簇的負荷曲線形態(tài)。類似其他文獻的做法[3]，筆者在進行聚類之前，對負荷數(shù)據(jù)進行了降維處理，基于負荷曲線的波動特性，采取分段刻畫曲線特征，從而降低了曲線數(shù)據(jù)維度。另外，對比了其他降維方法或選取特征指標的方式，開展對負荷特征的聚類，結果表明從聚類有效性指標判斷，k-shape 算法與k-means、DTW 算法相比綜合表現(xiàn)更佳。

2 算法原理

2.1 時間序列形態(tài)相似性度量

在進行時間序列相似度計算時，通常采用以下兩種方式：一是歐式距離，可以進行同等維度下的時間序列相似性的比較，但其對噪聲和異常點較敏感。二是動態(tài)時間彎曲距離（DTW），允許時間序列彎曲時間軸，可以度量不同維度下的時間序列的相似性，計算量較大，結果并不理想。為此，考慮使用互相關作為相似性判斷方式，互相關是用來比較兩個序列x=[x1,x2,...,xm]與y=[y1,y2,...,ym]相似性的一種統(tǒng)計測度方式。

理論上來看，同一類型的電力負荷，如同一個行業(yè)或同一家企業(yè)產(chǎn)生的負荷曲線，其形態(tài)特征及時序特征應該相似，除開外部敏感因素導致的差異可能對負荷特征造成影響。如果將具有相同形態(tài)的但存在時域差異的負荷曲線，進行平移。其不同時域下相似形態(tài)的曲線并為一個曲線類別，能更好地歸并用戶用電模式。有鑒于此，為比較不同負荷曲線的相關關系，將樣本X 的時間窗口適度平移使之與Y 全局對齊，以便進行兩序列全局形狀特征的比較。計算平移s 后的時間序列X，s為平移量，由此得出互相關序列CW（X,Y）=[c1,c2,...,cw]，其中，cw=Rw-m(X,Y),w ∈{1,2,...,2m-1}。

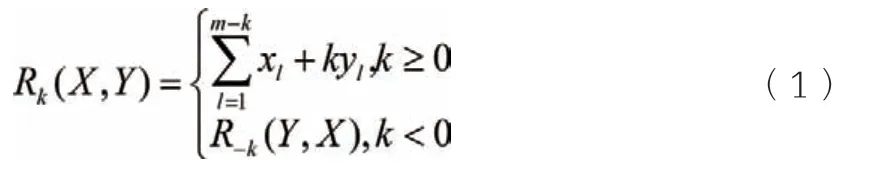
計算當cw達到最大值時w 的位置，相對于Y，X 的最佳位移量s=w-m。最后將互相關系數(shù)歸一化，互相關系數(shù)在-1，1之間，互相關系數(shù)越大，兩個序列正相關度越高，基于以上計算，提出時間序列相似性判斷D 距離量度的方法，即：

2.2 時間序列聚類中心的計算

聚類中心代表時間序列曲線形態(tài)特征，k-means 通過計算每類數(shù)據(jù)中各個坐標序列相對應數(shù)值的算術平均值來提取每類簇聚類中心，容易受到極端數(shù)據(jù)的污染。因此，提取聚類中心可以看作是一個優(yōu)化選擇問題，通過找尋與每類時間序列平方和最小的序列：

其中，c＊為使用該方法提取的最終聚類中心，ui是數(shù)據(jù)序列，c為尋優(yōu)迭代的聚類中心。該式表明，最優(yōu)聚類中心，擁有最大互相關系數(shù)。

3 K-shape 算法步驟

基于上述理論描述，利用互相關方法找出類的中心，迭代進行，聚類的具體步驟如下：

第一步：制定聚類數(shù)k，初始化每類聚類中心c。輸入預處理后的負荷數(shù)據(jù)。第二步：利用公式（1）依次計算負荷集中每一個負荷ui到各類中心c 的距離D，并將ui歸入到和c 聚類最小的類i 中。第三步：利用公式（2）提取每類聚類形態(tài)特征及每類聚類中心。第四步：重復第二步和第三步。設n為最大迭代次數(shù)，當達到最大迭代次數(shù)或者每類曲線集合不再發(fā)生變化時，停止迭代。第五步：輸出分類結果。

4 分析過程

利用部分國民經(jīng)濟主要行業(yè)近兩年每日的96點負荷數(shù)據(jù)，使用k—shape 算法進行聚類。考慮到電力數(shù)據(jù)的高維特征，考慮將負荷數(shù)據(jù)依據(jù)某種特征降維。如平均分段法，把負荷曲線分段聚合近似的方法來降低維度，具體來講，將時間序列平均分段，比如將96點負荷數(shù)據(jù)劃分為48點或24點數(shù)據(jù)，利用平均分段后的子序列的均值重構原始數(shù)據(jù)序列以實現(xiàn)數(shù)據(jù)的降維處理。然而，使用將時間序列平均分段并利用子序列的均值近似原始數(shù)據(jù)以實現(xiàn)數(shù)據(jù)降維的方式，對波動劇烈的時間序列，會丟失很多特征信息。如同平均值容易受到異常值的影響，對原始數(shù)據(jù)的信息刻畫存在失真一樣。這樣的重構降維方式無法準確反映原有序列的主要形態(tài)特征，從而使得曲線聚類出現(xiàn)偏差。為此，需要其他量化曲線的特征的方法，這種方法對極端數(shù)據(jù)點不敏感，或者可以更有效地刻畫波動型數(shù)據(jù)特征。從而通過有限的曲線特征值來捕捉原始曲線的高維信息，從而實現(xiàn)對高維數(shù)據(jù)的降維。

對高維曲線的降維，還是基于時間分段，并刻畫分段曲線的變化幅度和變化方向這一思路開展降維處理。由于負荷曲線在不同時點上的變化不同，利用在固定時間窗口內，負荷曲線的極差，即固定時間窗口內，最大負荷與最小負荷的差。當這個極差大于某個固定值的點的個數(shù)R，來刻畫曲線在固定時間內的波動程度。這個點在時間段內出現(xiàn)的次數(shù)越多，表明波動幅度越大。另外，除了刻畫曲線波動幅度，還應掌握曲線變化方向的信息。基于連續(xù)曲線斜率，利用觀測點前后曲線的斜率變化情況，來刻畫該點是否為曲線顯著的拐點，即斜率變化最大的邊緣點。對邊緣點的個數(shù)E 的統(tǒng)計，將有利于衡量負荷曲線變化方向特征。具體做法如下：

第一步：將每段負荷曲線U 分成m 段，若負荷曲線是n 點數(shù)據(jù)，則每段曲線有n/m 個數(shù)據(jù)點，計算每段曲線內的Ri（極差個數(shù)）和Ei（邊緣點個數(shù)），最后計算曲線總的R 和E。

第二步：若R 小于閾值a 并且E 小于閾值b，則使用每段平均值代表每段曲線。表明曲線段本身波動在可接受的范圍內，可由該段數(shù)據(jù)的平均值直接代替該段數(shù)據(jù)，從而實現(xiàn)以一個數(shù)據(jù)刻畫一段數(shù)據(jù)的降維作用。若R 小于閾值a 并且E 大于閾值b，表明曲線段內振幅不大，但曲線的斜率變化較為劇烈，則利用該段極大值或者極小值替代該段數(shù)據(jù)。

這種情況表明，該段曲線雖然波動幅度不大，但在波動范圍內，曲線趨勢發(fā)生較大變化，或由平緩變得傾斜，或由傾斜變?yōu)槠骄彙H僅利用該段內極大值或者極小值就可以刻畫這種變化特征。若在其他曲線中出現(xiàn)類似變化，則該段時間內的相似曲線極大或極小值會更為接近。若R 大于閾值a 并且E 大于閾值b，則保留原始數(shù)據(jù)。如此，該段曲線振幅較大，趨勢變化劇烈，直接用原始數(shù)據(jù)點表達這種異質性。簡言之，無振幅的數(shù)據(jù)，以一代眾，降維顯著，有振幅有變向的數(shù)據(jù)保留原始，不降維。

第三步，通過R 和E 刻畫現(xiàn)有曲線，計算現(xiàn)有數(shù)據(jù)的維度，若數(shù)據(jù)所降維度沒有滿足要求，則擴大閾值a 和b，繼續(xù)進行第二步，直到降維數(shù)據(jù)滿足要求。擴大a 和b 會使得曲線振幅和方向性減弱，平均點刻畫的情況增多，原始點刻畫的情況減少，從而進一步減少維度數(shù)。

為了便于與傳統(tǒng)方法比較，使用負荷曲線的統(tǒng)計數(shù)值特征，來刻畫原始數(shù)據(jù)并參與聚類，同樣起到了數(shù)據(jù)降維的作用。或者采用主成分分析方法先對負荷進行降維，再把降維之后的數(shù)據(jù)進行聚類。前者做法中，分別選取了負荷數(shù)據(jù)的統(tǒng)計特征，如均值、方差、變異系數(shù)、斜率、端點值等來刻畫負荷數(shù)據(jù)的曲線特征。后者做法上，使用主成分分析法，將96點負荷數(shù)據(jù)進行了降維，對降維之后的數(shù)據(jù)進一步開展了負荷聚類。從多項評價指標來看，k-shape 算法呈現(xiàn)出一定的算法穩(wěn)健特性。下文以某金屬品制造行業(yè)為例，分析分類的結果，圖1顯示該行業(yè)聚類得到的典型曲線。

圖1 某金屬品制造96點負荷曲線的聚類

聚類評價指標上選取了SIL 指標、DBI 指標和CP 指標進行聚類效果評價，具體見表1。其中，SIL指標將單個樣本與同簇樣本相似程度和其他類簇樣本相似程度進行比較，SIL 指標越高，聚類效果越好。DBI 指標計算簇內部距離之和與類外距離之比，其指標值越小，聚類效果越佳。CP 指標通過計算樣本集，每個樣本到該數(shù)據(jù)集聚類中心的平均距離來判斷每類簇緊密程度，指標值越低，聚類效果越好。

表1 各種算法的效果比較

首先，輸入降維數(shù)據(jù)，使用三種算法分別開展聚類分析，在不同聚類類別數(shù)時呈現(xiàn)的聚類評價如下：從聚類有效性指標來看，k—shape 算法與其余兩種算法綜合相比，在不同簇類上，SIL 的值相對較大，DBI 值相對較小，CP 值相對更小，說明較k-means和DTW 算法而言，k-shape 算法的表現(xiàn)更佳。

其次，在上述幾種算法的基礎上，區(qū)分了降維方式，對比不同降維方式下的分類效果。計算了該行業(yè)所有負荷曲線的統(tǒng)計指標，用以描述其曲線特征，所有負荷數(shù)據(jù)進行了標幺化處理后，做了描述性統(tǒng)計分析，選取了平均值、方差、極差、變異系數(shù)、中位數(shù)等五個主要的統(tǒng)計指標。在統(tǒng)計指標的基礎上，進行了k-means 算法的聚類。

另外，通過主成分分析法，將所有負荷數(shù)據(jù)進行了降維，前4個成分的信息總和超過70%，因此選取前4個成分進行k-means 聚類，并且通過與DTW 等算法進行了比較。以SIL 指標的取值為評價依據(jù)，分析結果見表2。

表2 不同數(shù)據(jù)處理方式的效果比較

以SIL 指標為依據(jù)，統(tǒng)計指標降維方式和主成分降維方式，并未在不同算法中并未體現(xiàn)出明顯的優(yōu)勢，表明上述兩種方式的降維對于刻畫曲線形態(tài)的作用不明顯，另外使用k-shape 算法對原始數(shù)據(jù)和降維數(shù)據(jù)聚類的對比依然顯示了較強的穩(wěn)健性。

5 結語

針對電力負荷數(shù)據(jù)高維度，多形態(tài)的特征和傳統(tǒng)算法的局限性，k—shape 的聚類算法顯示出了一定的優(yōu)勢。一方面在與k-means、DTW 算法的比較中顯示較好的聚類特性。另一方面，考慮到降維帶來的實際工作效率提升，同時對比了不同算法對降維數(shù)據(jù)的聚類效果，結果表明k-shape 算法較其他算法更為穩(wěn)健，且以統(tǒng)計指標、成分分析作為負荷曲線形態(tài)刻畫的方式和降維思路，在聚類效果上并未有所提升。本文對算法的驗證，有助于深刻把握電力負荷的行為模式和曲線特征，在分時電價模式下制定購售電策略，負荷預測等方面有實際作用，未來針對高維負荷數(shù)據(jù)的形態(tài)刻畫和聚類效率提升，仍有較大的研究空間。