帶虹吸式流道的軸流泵超駝峰起動特性分析

梁 興，胡鳳城，劉梅清，鄧飛，高剛剛

（1.南昌工程學院江西省精密驅動與控制重點實驗室，江西南昌 330099；2.武漢大學動力與機械學院，湖北武漢 430072）

0 引言

虹吸式出水流道由上升段、駝峰段、下降段等3 部分組成。在駝峰段常設置一臺真空破壞閥，當水泵停機時駝峰段出現真空，空氣通過真空破壞閥流入，將上升段、下降段分開，起到自然斷流的作用；水泵起動時，上升段水位不斷上升，達到一定壓力后頂開真空破壞閥排氣。虹吸式流道自然斷流的優越性，引起了科研人員的關注，取得了較多成果。譬如，Mimura［1］分析了虹吸式管道內流體夾氣運動的特點；Zhou 等［2］等分析了滯留氣囊對有壓流過渡過程的影響；周元斌［3］、馮建剛［4］、周大慶［5］等分別基于三維湍流數值模擬探討了虹吸式出水流道氣液兩相流動特點，模擬了斷流的形成過程。在帶虹吸式出水管的水泵起動方面，劉梅清等［6］建立了帶虹吸式出水流道的水泵起動計算數學模型，分析了泵站起動安全性；劉躍飛等［7］對預開啟真空破壞閥及真空破壞閥保持關閉等2種起動方式下的水泵起動過程分析了其優缺點。

上述研究及其應用從不同角度驗證了虹吸式流道自然斷流的優點。但隨著自然條件的改變，特別是汛期中超過駝峰段底部高程的外江水位也時常出現，這不僅造成了水泵停機時無法依靠駝峰自然斷流，也給超駝峰水位下水泵起動帶來了諸多問題［8，9］。針對此類問題，研究人員也設計出了蓄能式液壓啟閉閘門、活頁式快速閘門［10］等斷流方式，但是對超駝峰工況下水泵起動特性研究較少。本文針對某虹吸式流道，基于瞬變流理論建立水泵起動過渡過程計算模型，從閘門開啟時間、閘門預開開度、超駝峰高度等3 個因素討論超駝峰工況下的水泵起動特性。

1 超駝峰工況下的水泵起動過渡過程計算模型

圖1為泵站虹吸式出水流道示意圖，其流道水力參數如下：B0為泵站進水池水位，Z0為出水池水位，Bn-1、Bn分別為第n-1和n時段末的上升段水位，Fn-1、Fn分別為第n-1和n時段末的上升段水面面積，Zn-1、Zn分別為第n-1和n時段末的下降段水位。

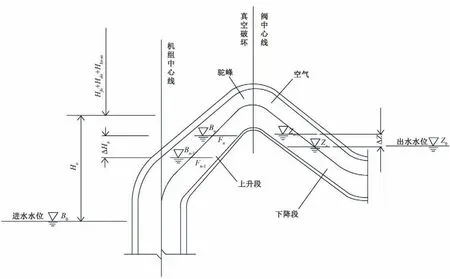
圖1 虹吸式出水流道示意圖Fig.1 Schematic diagram of siphon outlet channel

1.1 真空破壞閥邊界條件

假定流道內空氣壓力變化在等溫過程下進行，根據氣體狀態方程以及流道內水位變化情況可建立真空破壞閥的邊界條件如下［6］：

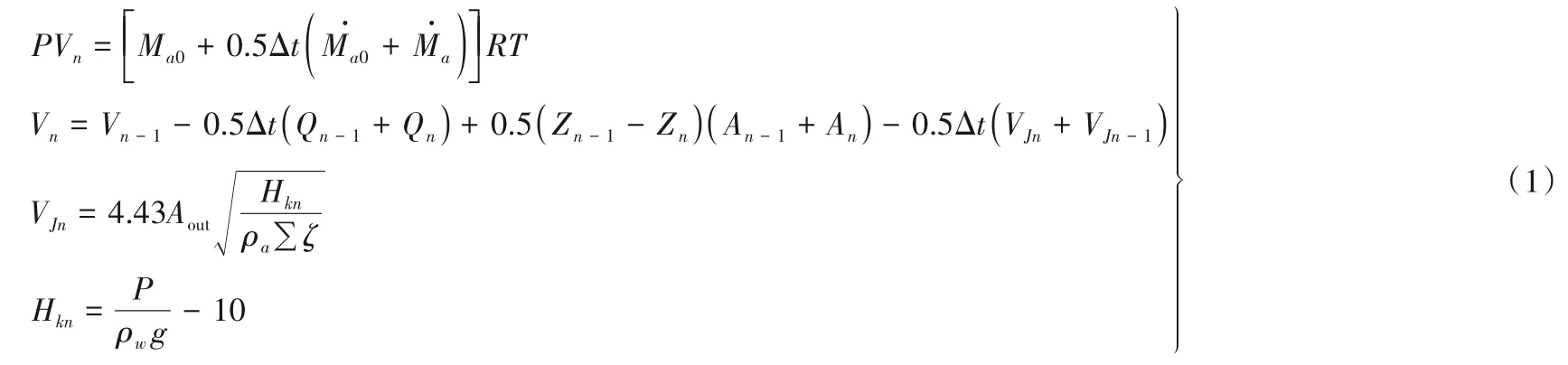
式中：Vn-1、Vn分別為第n-1 和n時段末的流道內空氣體積，m3；Ma0為第n-1 時段末流道內空氣質量，kg；分別為第n-1 和n時段末從真空破壞閥流出的空氣質量流量，kg/s；Qn-1、Qn分別為第n-1和n時段末的水泵流量，m3/s；An-1、An分別為第n-1和n時段末的下降段水面面積，m2；VJn-1、VJn分別為第n-1和n時段末從真空破壞閥流出的空氣體積流量，m3/s；Hkn為流道內空氣壓力相對值水頭，m；ρa為空氣密度，kg/m3；ρw為水的密度，kg/m3；∑ζ為真空破壞閥阻力系數。

1.2 水泵起動揚程計算

第n時段末的水泵揚程計算主要依據相似定律、水泵性能曲線及管道特性曲線獲得［6］，計算方法如式（2）所示。

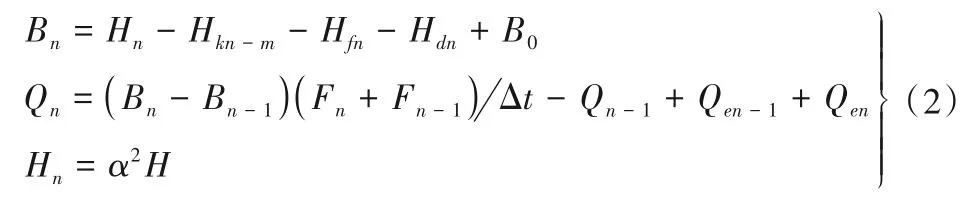
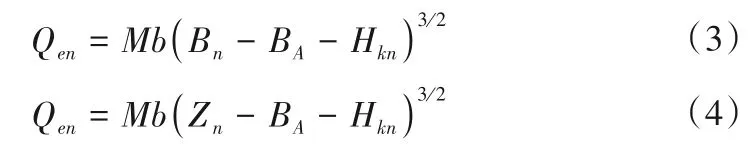
式中：Hn為第n時段末的水泵揚程；Hfn為第n時段末上升段的水頭損失，m；Hdn為第n時段末上升段的水面動壓力水頭，m；Qen-1、Qen分別為第n-1 和n時段末的駝峰溢流量，m3/s；M為駝峰溢流流量系數；b為駝峰寬度，m；BA為駝峰底面高程，m；F為駝峰處的橫斷面積，m2；α 為水泵無量綱轉速，α=n/nR；H為根據流量Q在水泵性能曲線上查出的水泵揚程，m，Q=Qn/α；Hkn-m為駝峰處空氣相對壓力，m。

當從上游向下游溢流時采用公式（3），反之則采用公式（4）。

1.3 下降段水位變化規律

隨著閘門的開啟，流道下降段內水體流動情況受出水池水位與流道內空氣壓力差的影響，其水位變化過程可在文獻［6］相應公式的基礎上，增加閘門水力損失項，即按下式計算：

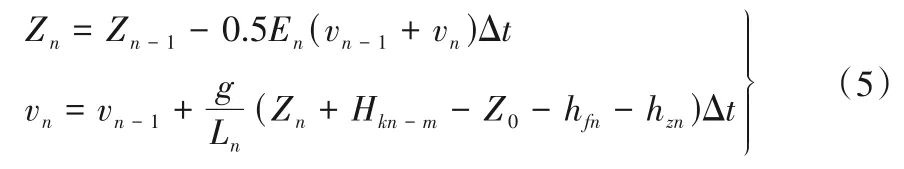
式中：En為第n時段中下降段橫斷面積與水面面積平均值的比值；vn-1、vn分別為第n-1和n時段末的下降段水流流速，m/s；Ln為第n時段末下降段水面以下流道長度，m；hfn為第n時段末下降段的水頭損失，m；hzn為第n時段末閘門損失，m。

2 水泵起動過渡過程數值模擬方案設計

某帶虹吸式流道的泵站，安裝4 臺軸流泵，水泵起動時間6 s，水泵設計揚程為7 m，設計流量24 m3/s，設計轉速150 r/min，其運轉特性曲線如圖2 所示。在虹吸管道駝峰制高點處安裝1臺真空破壞閥。流道駝峰底部高程27.7 m，閘門全開時間為120～300 s，汛期上游水位約在23 m，超駝峰高度范圍為0～3.3 m。在外江水位超駝峰狀態下，泵站出口閘門處于關閉狀態，考慮到軸流泵流量大、常開閥起動的特點，在軸流泵起動時將出口閘門預開一定開度，避免軸流泵開機后水流涌至閘門處使流量突然降低導致揚程急劇增加，影響水泵起動穩定性。采用正交試驗法［11，12］設計水泵起動過渡過程3 因素3水平方案，其中3因素為閘門開啟時間、閘門預開開度、超駝峰高度，各因素設置高中低3個水平，具體如表1所示。

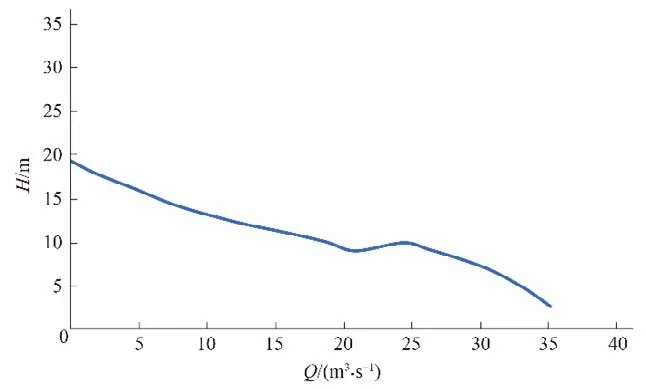
圖2 額定轉速下泵運轉特性曲線Fig.2 Pump operation characteristic curve under rated speed

3 水泵起動過渡過程特性分析

3.1 泵起動特性極差分析

針對表1 開展水泵超駝峰工況下起動特性分析，以最大起動揚程值（無量綱，設計揚程為基準值）和最大倒流量（無量綱，設計流量為基準值）為評估指標，其結果如表2所示。依據極差分析方法分別計算閘門開啟時間、閘門預開開度、超駝峰高度等3個因素影響，其結果如表3所示。

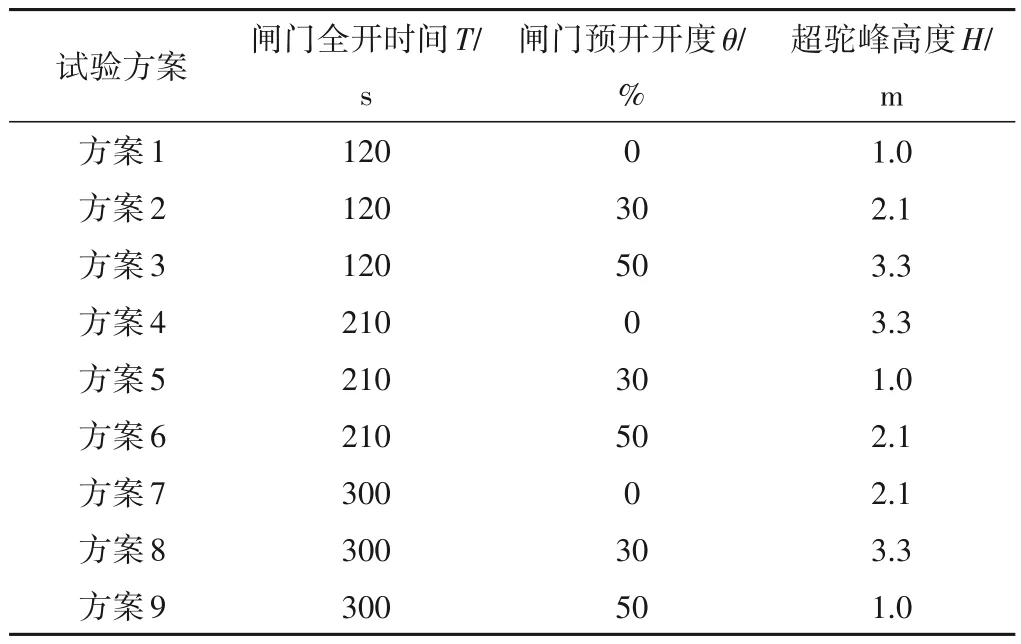
表1 泵起動特性正交試驗表Tab.1 Orthogonal test table of pump starting characteristics

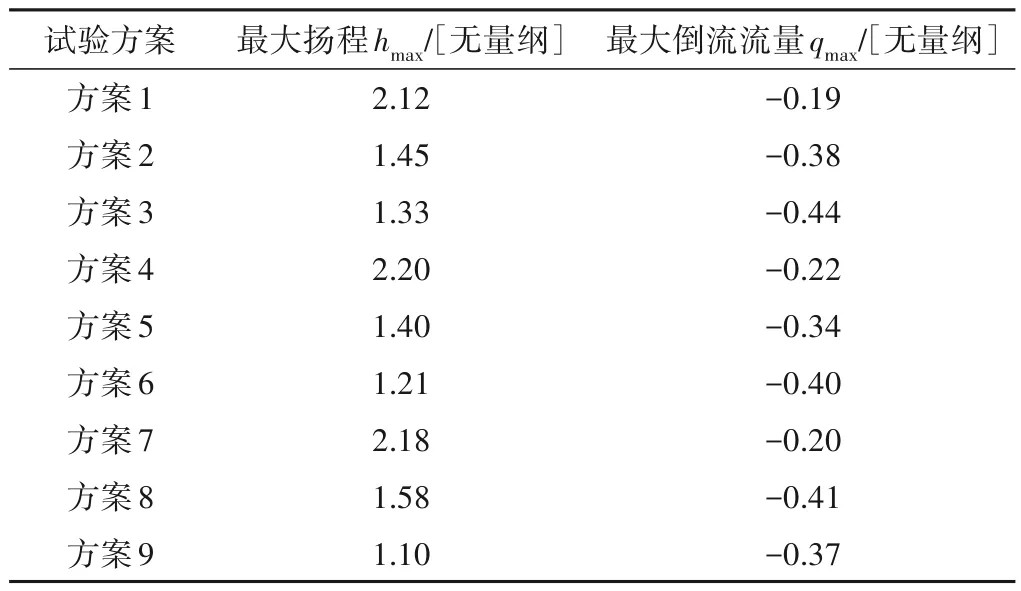
表2 泵起動特性正交試驗結果Tab.2 Orthogonal test results of pump starting characteristics

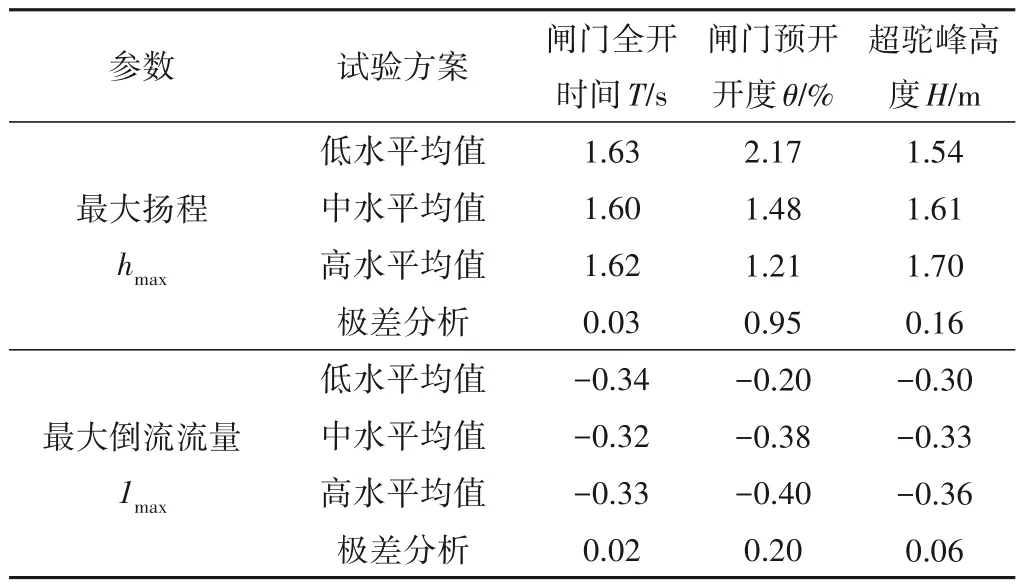
表3 各因素對評估指標的影響分析Tab.3 Impact analysis of various factors

由于超駝峰情況下，外江水位高于內江水位，在閘門打開瞬間，存在一定的倒流現象，該現象也被仿真結果所驗證（如表2 所示），隨著水泵揚程快速提升，倒流現象常在3 s內消失。分析表2、3可知，隨著閘門全開時間的延長，最大無量綱揚程和最大倒流流量均是先減小后增加；隨著閘門預開開度的增加，最大無量綱揚程逐步降低，最大倒流流量逐步增加；隨著超駝峰值的增加，最大無量綱揚程逐步增大，最大倒流流量也逐步增加。對最大無量綱揚程的影響權重分析可知，閘門預開開度影響最大，閘門全開時間影響最小；對最大倒流流量影響權重分析可知，閘門預開開度影響最大，其余兩者影響大小相當。

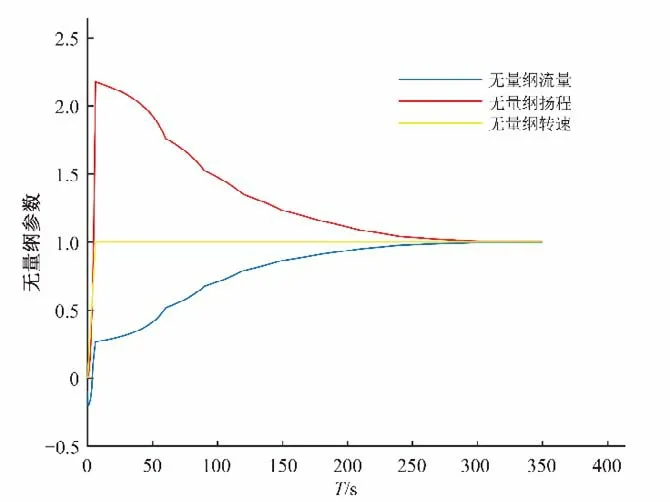
圖4 方案7水泵起動過渡過程Fig.4 Starting transition process in scheme 7

圖3、4 為典型工況下水泵起動特性變化曲線，揚程和流量的變化規律也和上述分析一致。因此，軸流泵起動過程中，若揚程較高則有較大可能穿越“馬鞍區”，若倒流流量較大，則增加了水泵起動難度。綜合考慮相關影響，選擇閘門240 s 全開，預開30%作為泵最優起動方案。

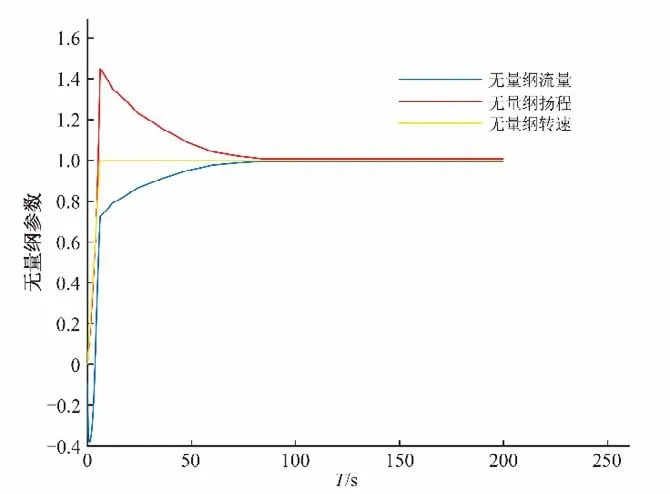
圖3 方案2水泵起動過渡過程Fig.3 Starting transition process in scheme 2

3.2 泵最優起動方案分析

當采用“閘門240 s 全開，預開30%”作為泵最優起動方案，當上游水為23 m，下游水位為31 m，此時揚程及超駝峰值最大，故為最不利工況，泵起動特性如圖5所示。

圖5中，當水泵起動時，揚程先快速提升至最大值后逐步減小至穩定值，流量則先開始倒流，隨著水泵轉速的提升，倒流在3 s內快速變為正流量，并逐步達到穩定值。當水泵達到額定轉速時，揚程達到最大值（無量綱揚程1.57，揚程10.99 m），軸流泵穩定運行范圍為0.5～11.5 m，水泵起動過程中未穿越“馬鞍區”，故該方案符合要求。另外，最大揚程在水泵達到額定轉速時出現，該峰值主要受閘門處水力損失的影響，當閘門預開開度較小時，揚程峰值較大，反之則較小。

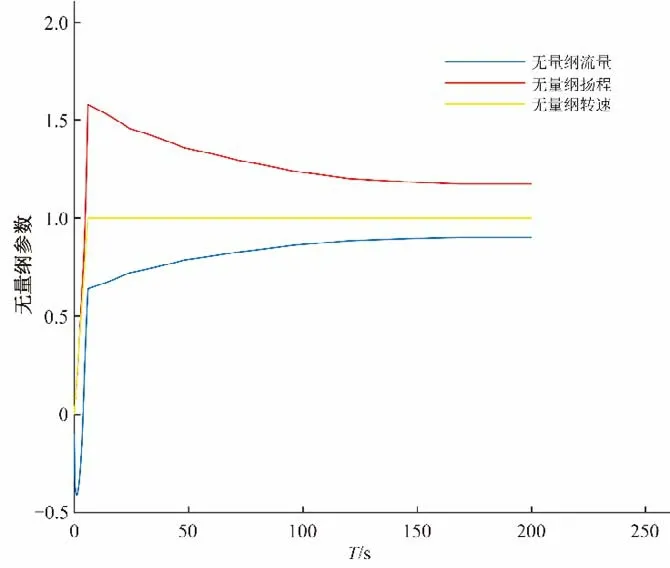
圖5 最不利工況下水泵起動特性Fig.5 Starting characteristics under the most unfavorable conditions

4 結論

針對帶虹吸式出水流道的泵站超駝峰運行狀態，建立了數值仿真模型，采用正交試驗法分析閘門開啟時間、閘門預開開度、超駝峰高度等3個因素影響對起動揚程和流量的影響，主要結論如下。

（1）起動最大揚程主要受閘門預開開度的影響，閘門預開開度越小，起動揚程越大，閘門全開時間對其影響最小；倒流流量的首要影響因素也是閘門預開開度，閘門預開開度越大，最大倒流流量就越大，其他兩個因素對其影響較小，且權重相當。

（2）依據正交試驗結果，選取“閘門240 s全開，預開30%”作為泵起動方案，在最不利情況下，水泵揚程最大值為10.99 m，處于機組穩定運行范圍，該方案符合要求。