基于改進組合賦權法的區域水資源承載力評價

李治軍，王濤

（1.黑龍江大學水利電力學院，黑龍江哈爾濱 150080；2.黑龍江大學寒區地下水研究所，黑龍江哈爾濱 150080）

0 引言

水資源是人類生存和社會發展的必要資源，隨著社會的進步與發展各行業對水資源的需求量不斷增加，如何解決供需不足的矛盾已經成為我國經濟社會可持續發展的重要問題［1］。水資源承載力由我國學者于20 世紀80 年代末所提出，水資源承載力是區域生態環境建設和確定社會經濟健康發展方向的基礎，是對水資源在時間和空間上的一個度量尺度［2］。研究水資源承載力不僅有利于弄清生態環境、社會經濟與水資源的空間關系，更是在水資源安全戰略研究和可持續協調發展中起到了不可或缺的作用［2］。

現如今水資源承載力評價計算權重的方法大致可以分為兩類，一類是有相關領域專家判定指標間的相對重要程度的賦權方法，如：層次分析法（Analytic Hierachy Process，AHP），該種方法主觀性強，人為影響要素較大，不適用于具有不確定性的定量評價中［3］。在實際的復雜系統中，系統諸要素間是相互作用的，不同層次間的元素也是相互影響的，采用AHP 方法求解必然存在不準確和不科學之處。另外一類是依據各指標樣本數據提供的信息進行的賦權方法，如熵權法（Entropy Weight Method，EWM）該方法杜絕了主觀要素的影響，但是難以表達出指標間相互影響的關系［4］。而且傳統熵權法具有一定缺陷，每個熵間細微的變化在一定情況下可能會導致各指標熵權間的成倍變化［5］。

針對以上問題，本文采用網絡層次分析法（Analytic Network Process，ANP）與改進的熵權法共同計算組合權重，Saaty 提出的ANP 法能夠解決層次分析法（AHP）模型難以準確計算具有依賴性、反饋性的決策問題，揭示指標集內外部間存在的相互作用關系，適用于無法精確建模為層次結構的經濟社會等問題［6］。通過改良后的熵權法模型能夠解決由于每個熵間的細微變化而導致成倍增長的問題。計算出的權重進行組合賦權更好的提高了權重的穩健性。本文所提供的方法為日后水資源承載力評價研究提供新思路和參考。

1 研究方法

1.1 指標識別及構建評價體系

水資源承載力評價模型的建立是一個系統的工作，指標的確定需要考慮多方要素的影響，本文指標選取按照SSHIO 原則（系統性Systematicness、特定性Specificity、層次性Hierarchy、獨立性Independence、可操作性Operability）并通過閱讀大量文獻對已有研究結果進行總結并進行專家咨詢并結合研究區域實際情況，基于WEE（水資源Water Resource－經濟Economics－生態Ecology）建立評價體系［7］。本文建立以水資源、經濟、生態為一級評價指標，以人均水資源量、產水模數、降雨量等16個指標作為二級評價指標建立蕪湖市水資源承載力評價體系，見圖1。

1.2 DEMATEL確定影響關系

決策實驗室法（Decision Making Trial and Evaluation Laboratory，DEMATEL）是Bottelle 研究所于1971 年提出的一種決策方法，能夠有效地確認準則或各元素之間的因果關系及相互影響程度，通過建立指標間因果關系來研究和解決較為復雜的系統問題［8］。通過DEMATEL確定影響關系具體步驟如下：

（1）確定指標并判斷關系：分析評價體系中選取的各指標元素，通過調查問卷的方式判斷各元素直接的相互關系，各指標元素記為Xi（i=1，2，3，…，16）。

（2）確定系統要素間直接影響關系，構建直接影響關系矩陣D，直接影響關系矩陣通過專家對各指標間影響大小判斷形成。

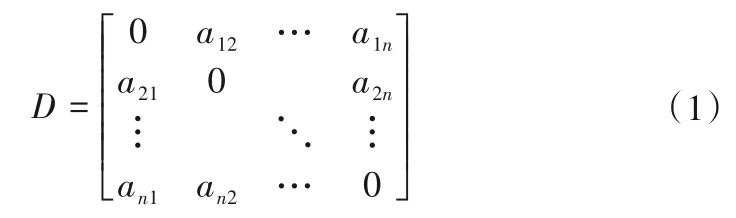
式中：n為指標個數；a21為指標a2對指標a1的影響程度且對角線均為0。

（3）影響關系矩陣標準化處理。

（4）構建綜合影響矩陣。

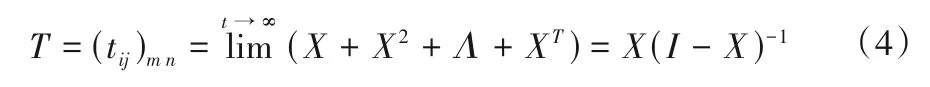
1.3 利用ANP確定指標權重

ANP 是層次分析法AHP 的基礎上進一步改造、完善的，它考慮了同一等級各指標要素間的相互關系，是一種更加科學準確的決策方法［9］。使用ANP確定指標權重計算過程如下。

與治療前相比，觀察組和對照組治療后1、2個月的骨保護素水平均顯著升高(P<0.05)；其中觀察組治療后2個月骨保護水平顯著高于治療后1個月(P<0.05)。組間相比，治療前和治療后1個月，觀察組牙周組織骨保護素水平與對照組相比均無統計學差異(t=1.765, t=1.766；P>0.05)；治療后2個月，觀察組牙周骨保護素水平顯著高于對照組(t=5.925，P<0.05)(表1)。

（1）根據DEMATEL 求得綜合影響矩陣建立水資源承載力評價的ANP 的網絡結構，見圖2。圖2 中雙箭頭表示兩簇中的節點指標互相影響，環向箭頭表示該簇內節點指標相互影響［9］。

圖2 水資源承載力評價網絡結構圖Fig.2 Water resources carrying capacity evaluation network structure diagram

（2）根據1～9 評估尺度表［10］，見表1。對每個指標重要性程度進行判別構建判斷矩陣，對判斷矩陣進行歸一化處理后進行一致性檢驗，從判斷矩陣中求解最大特征值、特征向量，通過得到的特征向量構建未賦權的超矩陣。

表1 1～9尺度表Tab.1 1～9 scale

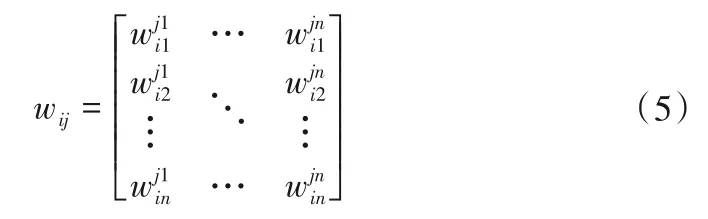
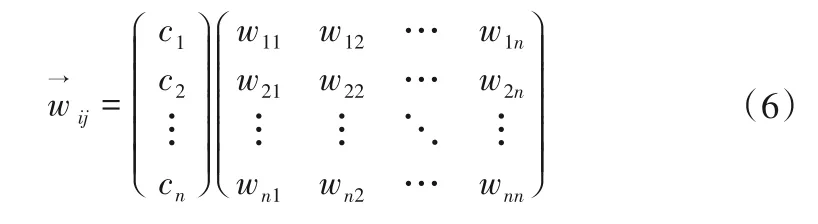
（3）對w矩陣進行歸一化處理，在對矩陣賦權得到賦權超矩陣。

1.4 利用改進熵權法確定指標權重

1.4.1 熵權法的基本原理

熵權法是一種依靠評價指標體系中各指標的相關數據多少來進行確定指標權重的賦權方法，熵權法是一種客觀賦權法［12］。熵權法是管理科學中經常使用的技術手段，它利用數據本身的無序化和不均勻程度來體現指標中含有信息量多少，進而判斷該指標對目標決策的影響程度［13］。熵權法計算步驟如下：

（1）將構建的判斷矩陣進行數據標準化處理得到標準化矩陣Yij。

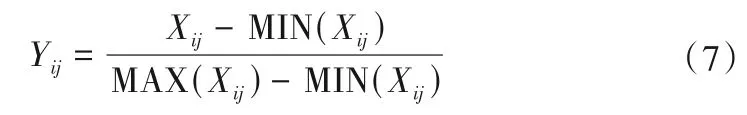
（2）計算各指標的熵值Ej。

（3）根據求出熵值，求解各指標權重。

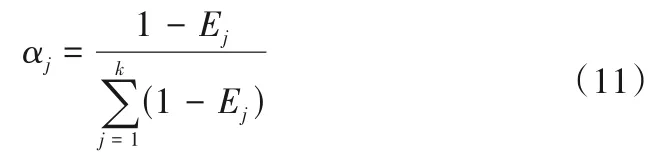
1.4.2 熵權法的改進

上文介紹了傳統熵權法的基本原理，通過實際應用、分析，這種傳統熵權法具有一定缺陷，當熵值趨近于1時，每個熵間細微的變化都會導致各指標熵權間的成倍變化［14］。如：當取4 個指標的熵值分別為0.999、0.998、0.997、0.996時，這幾個指都趨近1，這4 個指標對目標決策的影響程度都相接近。但通過傳統熵權法進行計算，這4 個指標的出權重為0.1、0.2、0.3、0.4，其權重成倍數變化，不符合各指標對目標決策的真實影響程度。根據此類情況，本文采用改進的熵權法模型進行計算。步驟如下：

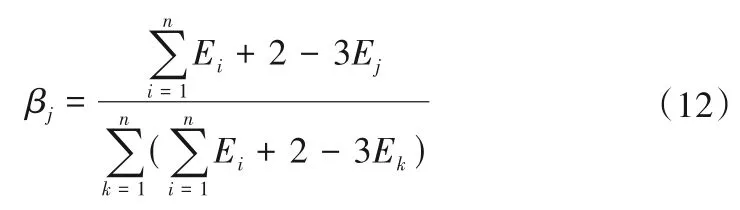
根據權重系數規則，各指標權重相加等于1，同時各指標權重需為大于0小于1的數，該公式均滿足此要求。扔取4個指標熵權分別為0.99、0.98、0.97、0.96時通過改進的熵權法計算得出權重為0.209 1、0.236 4、0.263 6、0.290 9可知指標權重不會由于每個熵間的細微變化而導致成倍增長。

1.5 組合權重的計算

考慮到主觀權重不能反映數據信息，而客觀權重無法體現決策者的主觀意愿，從某種意義上講，主觀權重向量和客觀權重向量都不是最優的權重向量［15］。因此，為了權重的穩健性，需要進行主客觀組合賦權，保證組合后的權重更為合理有效［16］。考慮到主客觀權重特性，本文采用乘法合成法進行組合權重。步驟如下：

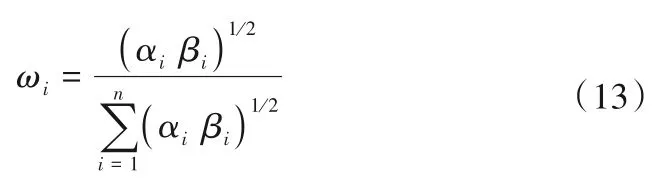
1.6 利用FCE計算綜合評價值

本文采取模糊綜合評價法計算水資源承載力最終評價值，模糊綜合評價法是借助模糊數學隸屬度理論將定性的評價轉換成定量評價，使一個受到多方因素制約的對象做出一個清晰、準確的評價。指標類型為“+”的隸屬度計算公式如下［17］。

此公式為指標類型為“效益型（越大越好）”的隸屬度計算公式，若指標類型為“成本型（越小越好）”將公式中“＞”與“＜”互換位置即可［17］。

2 實例分析

2.1 研究區域概況

蕪湖，位于安徽省（E118°21'，N31°20'）。坐落于長三角西南部，地處青戈河、漳河、裕溪河交匯處，是華東重要的工業基地、綜合交通樞紐。該市為亞熱帶濕潤季風氣候，光照充足，雨量充沛，四季分明［18］。蕪湖降雨充沛，年降雨量1 200 mm，但年內降水分布不均，主要集中在春季、梅雨季節和初冬，無霜期每年達219～240 d［18］。

蕪湖市雖水資源豐富，但據環保局監測資料顯示該地區水污染趨勢加劇，青戈河水體污染嚴重，部門指標超標，出現富營養化、有機物污染等問題［18，19］。且水體污染導致可利用地表水資源減少，水資源供需矛盾等問題［19］。

2.2 數據來源

本文各指標數據來源于蕪湖市水務局（https：//shuiwuju.wuhu.gov.cn/）提供的《蕪湖市水資源公報》、安徽省統計局（http：//tjj.ah.gov.cn/）提供的《安徽統計年鑒》、以及部分參考文獻。

2.3 計算結果

根據上文所介紹的模型，按照第1 節所提供的方法進行計算，計算結果見下表所示。改進的熵權法與傳統熵權法權重對比見表2，未賦權的超矩陣見表3，賦權超矩陣見表4，指標權重見表4，ANP 計算指標權重見表5，蕪湖市水資源承載力最終權重見表6，蕪湖市2006-2016年評價值見表7。

表2 改進的熵權法與傳統熵權法權重對比Tab.2 Weight comparison between improved entropy weight method and traditional entropy weight method

表3 水資源承載力評估指標的未賦權超矩陣Tab.3 Unweighted supermatrix of water resources carrying capacity evaluation index

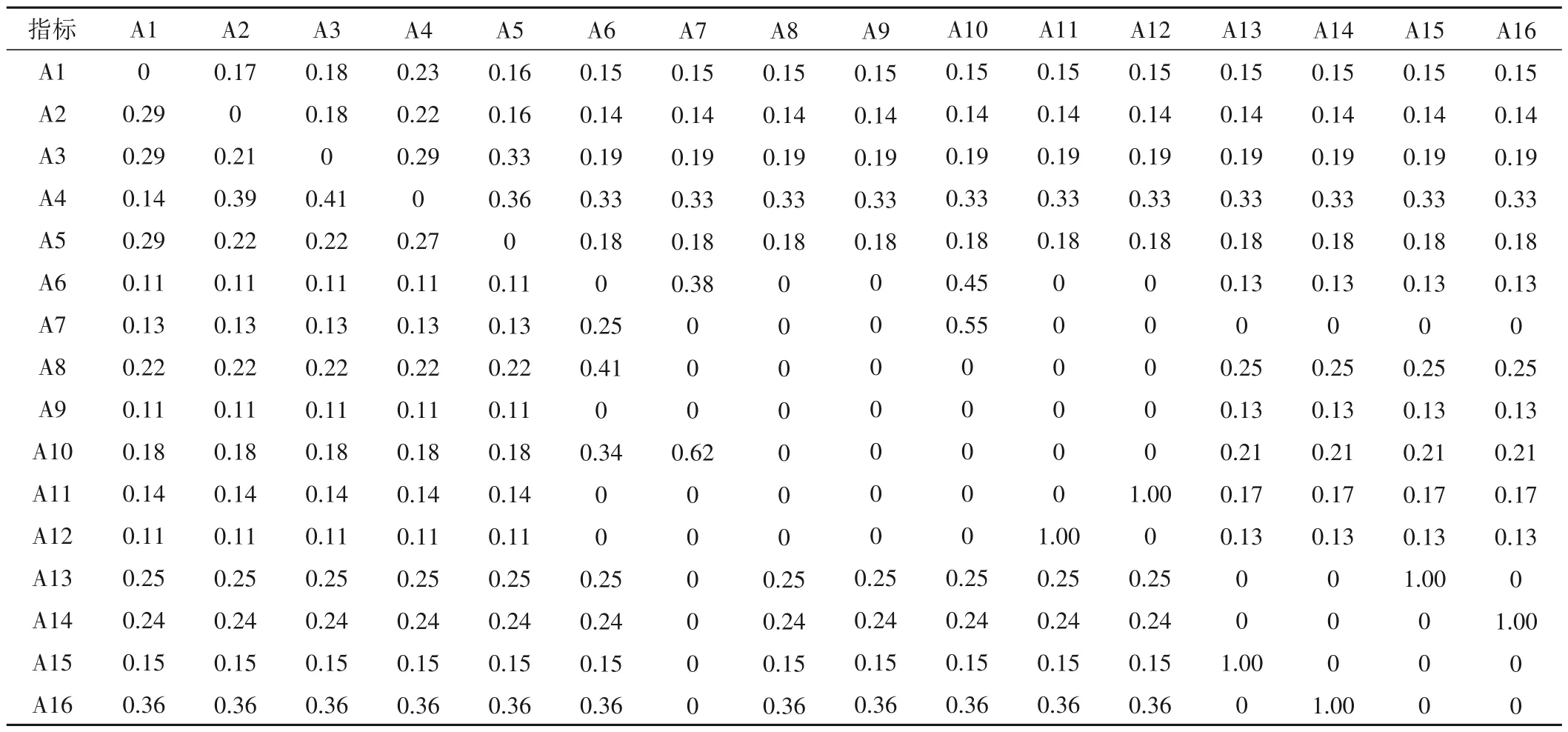
表4 水資源承載力評估指標的賦權超矩陣Tab.4 Weighted supermatrix of water resources carrying capacity evaluation index

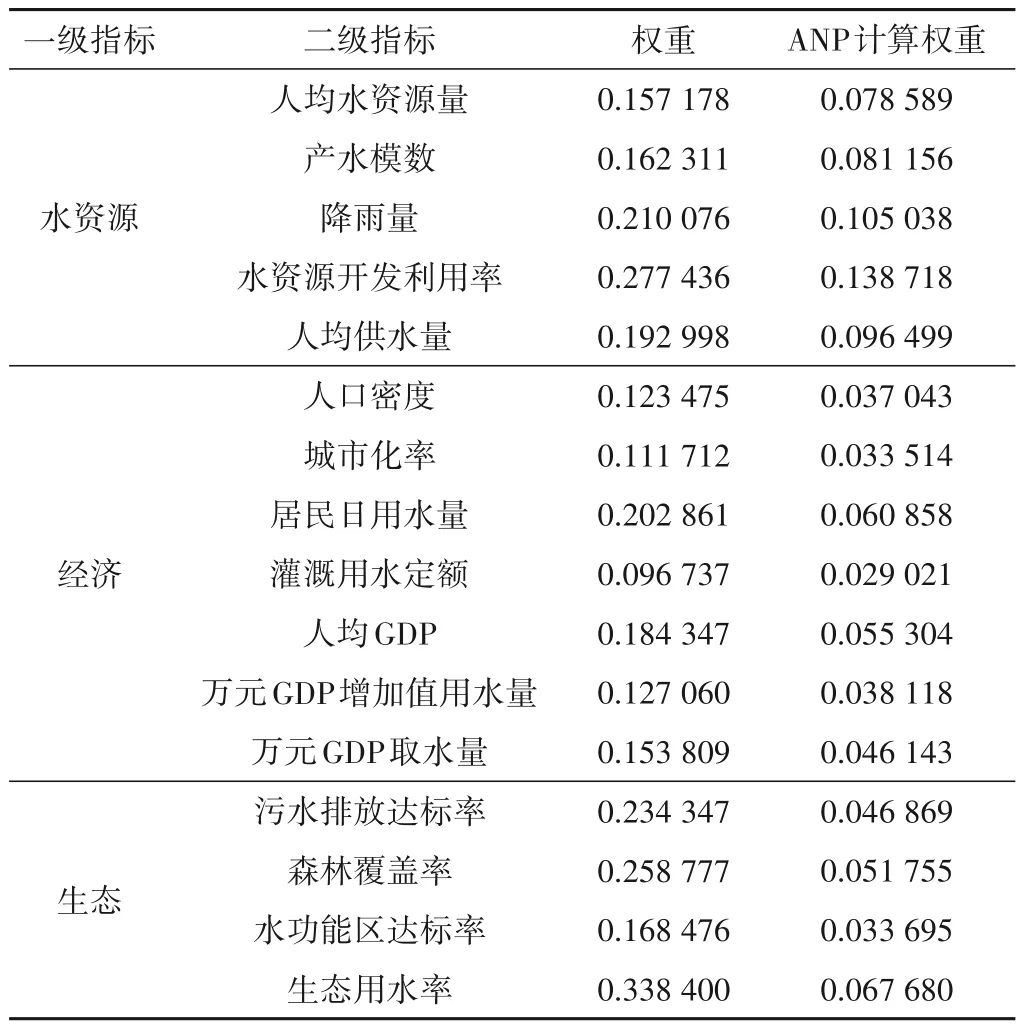
表5 ANP 計算指標權重Tab.5 ANP calculation index weight

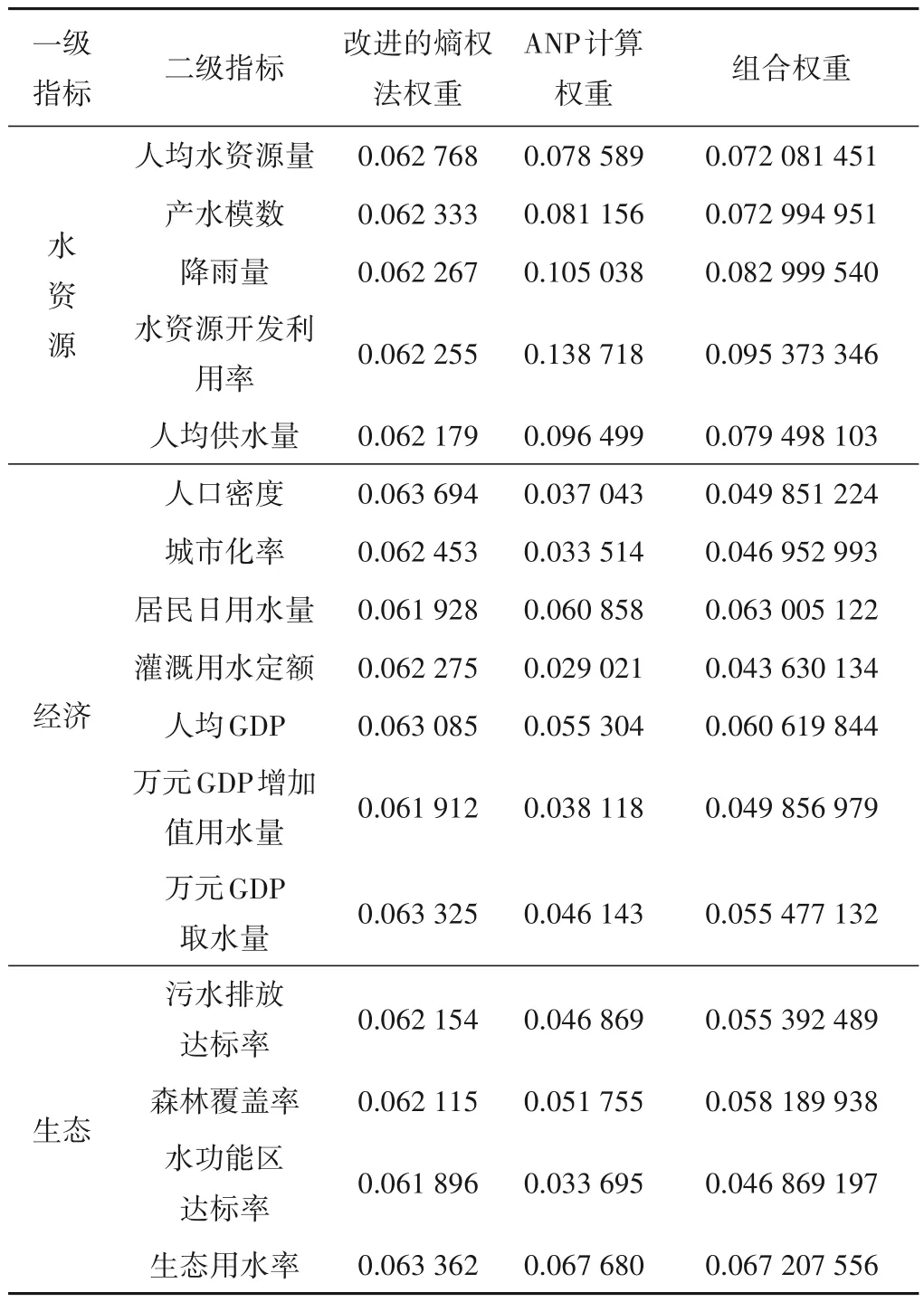
表6 蕪湖市水資源承載力最終權重Tab.6 Final weight of water resources carrying capacity in Wuhu City

表7 蕪湖市水資源承載力評價得分Tab.7 Water resources carrying capacity evaluation score of WuHu City

3 討論

本文通過改進組合賦權模型的水資源承載力評價，充分考慮了蕪湖市水資源承載力評價體系間各指標復雜的關系，可以精準地計算出指標權重，能夠合理的確定指標間權數分配，提高了指標權重的客觀性、精確性、科學性。

本文通過改進的組合賦權模型的對蕪湖市水資源承載力進行評價與前人研究成果進行比較，其中孫康等［20］通過層次分析法計算權重得出蕪湖市水資源承載力評價值0.4～0.6之間，總體趨勢除2011 年、2013 年以外總體上升，水資源承載力處于臨界狀態。與本文研究成果相比基本相符。

從ANP 空間網絡結構來看，各指標層之間存在相互影響關系其簇內節點也存在著相互影響的關系。模型計算結果顯示，一級指標層水資源在所有的指標層中重要程度最大，影響其他指標程度最大。在一級指標水資源當中，其各指標權重均在平均值之上，對水資源承載力影響程度較大，其中水資源開發利用率指標影響度最大。一級指標經濟中，居民日用水量、人均GDP 影響度大。一級指標生態中，生態用水率影響程度最大。由于降雨量受人為干擾可能性較小，因此人均水資源量、產水模數、水資源開發利用率、人均供水量、居民日用水量、人均GDP、生態用水量與其他指標關聯性強，對這些指標進行改變，對其他指標影響最大，水資源承載力提升更加明顯。

由圖3 可知該區域水資源承載力上升最快為2015 年到2016年，綜合評價值上升0.060 9，查詢該年數據可知，主要原因是水資源方面：該年降雨充沛，水量豐富，人均水資源量明顯提升。經濟層面：該年人均GDP 首次突破7 萬元，隨著節水設施的推廣該年萬元GDP 取水量首次進入100 m3。生態方面：該年污水排放達標率突破85%，水功能區全部達標。

通過對熵權法的改進優化解決了傳統熵權法每個熵間的細微變化而導致權重成倍增長的現象。使計算出的權重更能準確地表現出各數據指標對目標決策的真實影響情況。采用AHP 和改進的熵權法計算組合權重的方法既尊重了專家在以往評價計算中的經驗，又客觀的結合了數據指標使評價結果更加真實、準確，能夠科學的評估區域水資源承載力綜合情況，能夠對水資源開發利用加以參考作用。

4 結論

采用改進組合權重水資源承載力評價模型對蕪湖市水資源承載力進行評價與前人研究結果對比評價結果相符說明該模型在水資源承載力上應用行之有效，該模型評價結果顯示蕪湖市水資源承載力綜合評分位于0.407 1～0.637 0 之間，其最低值2006 年（0.407 1），最高值為2016 年（0.637 0）該研究區域水資源承載力呈上升趨勢，說明該區域對于水資源承載力的管理方式行之有效，未來可以繼續保持。

根據研究區域實際情況選取指標體系，構建綜合評價模型。不僅能夠對水資源承載力進行靜態評價，還可以對不同年份、不同時期水資源承載力進行動態評價。評價結果相互對比，相互激勵。找尋水資源承載力薄弱部位，有針對性地對提升區域水資源承載能力對癥下藥。