基于小波包分解的EHO-ELM 與EHO-DELM日徑流多步預報模型研究

李新華，崔東文

（1.云南興電集團有限公司，云南文山 663000；2.云南省文山州水務局，云南文山 663000）

0 引言

日徑流時間序列預報被廣泛應用于水庫實時運行調度、水電系統經濟運行及航運、防洪等領域，尤其是時間序列分析及多步預報一直是日徑流預報研究領域的熱點和難點。目前日徑流時間序列預報方法有自回歸模型（Auto Regressive，AR）［1］、人工神經網絡（Artificial Neural Network，ANN）［1］、自適應神經模糊推理系統（Adaptive Neural Fuzzy Inference System，ANFIS）［1］、長短時記憶神經網絡（Long Short-Term Memory，LSTM）［2］、支持向量機（Support Vector Machine，SVM）［3-5］等，但還沒有一種統一和普遍適用的方法。由于日徑流受天文、氣象、地理等多重因素的影響，常表現出較強的非線性、非平穩性和多尺度等特征，傳統單一預測方法難以獲得較好的預報效果。當前，基于“分解方法+預測器”模式的多種方法混合預報模型被嘗試用于日徑流時間序列預報研究，并取得較好的預報效果。孫望良［2］等引入變分模態分解（Variational Mode Decomposition，VMD）、去趨勢波動分析（Detrended Fluctuation Analysis，DFA）和LSTM方法，提出DFA-VMD-LSTM 日徑流預報模型，并將其應用于三峽水庫日徑流預報研究，取得較好預報精度；黃景光［3］等基于小波分解（WD）方法和SVM 建立組合日徑流預報模型，將其應用于宜昌站日徑流預報，驗證了該模型具有更好預報穩定性；黃巧玲［4］等將小波變換與支持向量機結合，提出小波支持向量機回歸模型（Wavelet Support Vector Machine，WSVR），利用所建立的WSVR 模型對張家山站日徑流進行預報，結果顯示WSVR 模型可有效模擬和預報日徑流；任化準［5］等融合WD 方法、粒子群優化（Particle Swarm Optimization，PSO）算法和SVM，提出WPSO-SVR 日徑流預報模型對金沙江中游石鼓站日徑流進行預報，表明該模型在日徑流預報中具有較強的適應性。然而，上述模型［2-5］及大多數日徑流預報僅針對預見期為1 d 的單步預報，在實際應用中，預見期為1 d 的單步預報無法滿足日徑流預報實際需求，往往需要根據歷史數據實現更多尺度的超前多步預報，即實現未來更為長遠的日徑流時間點預報［6］。

為提高日徑流時間序列多步預報精度，針對上述問題，本文基于以下因素，提出基于小波包分解（WPD）、象群優化（EHO）算法和極限學習機（ELM）、深度極限學習機（DELM）多種方法的WPD-EHO-ELM、WPD-EHO-DELM 日徑流時間序列混合預報模型，并應用于云南省景東水文站日徑流時間序列多步預報。①WPD 能同時將低頻、高頻信號進行再次分解，提取出更具規律的子序列分量，克服WD 方法不對高頻信號再次分解的不足；同時，WPD較小的分解層即能獲得較好的分解效果。②目前，日徑流時間序列預測器主要有BP 神經網絡、SVM、LSTM等，但BP 神經網絡模型存在設置參數多、易陷入局部最優等缺點；SVM 模型存在對參數敏感、大容量樣本預報中表現不佳等不足；LSTM 模型雖然預測性能較好，但存在內存資源消耗大、運行時間長等缺陷。ELM、DELM 預測器不但預測性能好，且在日徑流預報研究中應用不多。③ELM、DELM 網絡輸入層權值和隱含層偏置是制約其性能提高的關鍵因素，本文采用EHO 算法優化ELM、DELM 輸入層權值和隱含層偏置，以期提高ELM、DELM預測器性能。

1 研究方法

1.1 小波包分解（WPD）

小波包分解（WPD）衍生于小波分解（WD），與之不同的是，WD 只對低頻信號再次分解，不分解高頻信號，而WPD 同時將低頻、高頻信號再次分解，并能根據信號特性和分析要求自適應地選擇相應頻帶與信號頻譜相匹配。對于波動信號，采用WPD能夠凸出信號的細節特征。小波包分解算法公式［7-10］為：

重構算法為：

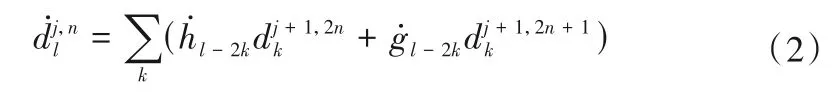
1.2 象群優化（EHO）算法

象群優化（EHO）算法是Wang等人于2016年提出了一種新的群體智能優化算法。EHO 算法源于自然界中大象的畜牧行為，并基于以下假設：①象群分為幾個氏族，每個氏族中母象作為首領；每一代中，一定數量的雄象會離開氏族。②女族長是氏族中適應度最好的大象，每頭大象的位置根據其位置和女族長的位置進行更新；族長的位置根據氏族中心的位置進行更新。③EHO 算法包括氏族更新操作和分離操作兩個階段，氏族更新代表著局部搜索，雄象離開氏族執行全局搜索［11，12］。

EHO算法數學描述如下［11，12］：

（1）氏族更新。隨機初始化大象種群，將大象種群分為n個氏族，每個氏族中有j頭大象，在每次迭代中，每頭大象j的位置都會隨氏族ci中族長（適應度值最好的位置）移動。位置更新數學描述為：

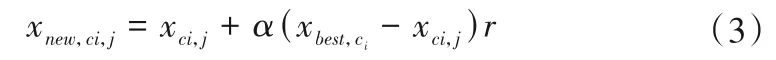
式中：xnew，ci，j表示隨氏族ci中第j頭大象更新后的位置；xci，j表示氏族ci中第j頭大象上一代位置；xbest，ci表示氏族ci中適應度值最好的位置；α∈[0，1]表示最佳女族長對大象個體xci，j的影響比例因子；r表示［0，1］范圍內的隨機數。

氏族ci中女族位置更新數學描述為：

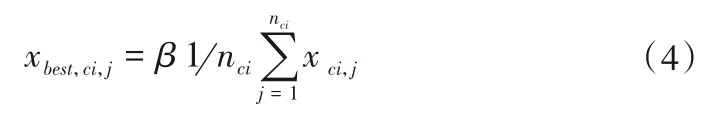
式中：β∈[0，1]表示氏族中心控制參數；nci表示氏族ci中大象的數量；xci，j表示氏族ci中大象個體。

（2）氏族分離。EHO 算法中，每個氏族ci中具有最差適應度函數值的恒定數量的大象會被移動到新的位置。其位置更新數學描述為：

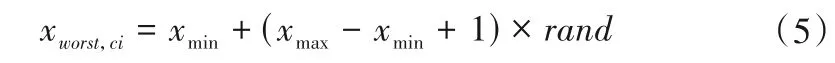
式中：xworst，ci表示氏族ci中具有最差適應度函數值的大象位置；xmax、xmin表示搜索空間上下限值；rand表示［0，1］范圍內的隨機數。

1.3 極限學習機（ELM）

極限學習機（ELM）是一種廣義的單隱層前饋神經網絡，具有較快的學習速度和良好的泛化能力。給定M個樣本Xk={xk，yk}，k=1，2，…，M，其中xk為輸入數據，yk為真實值，f(·)為激活函數，隱層節點為m個，ELM輸出可表示為［13，14］：

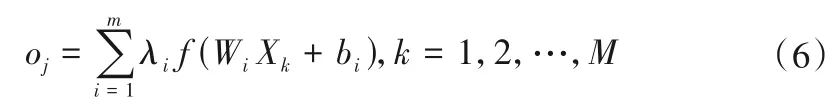
式中：oj為輸出值；Wi={ωi1，ωi2，…，ωim}'為輸入層節點與第i個隱含層節點的連接權值；bi為第i個輸入節點和隱含層節點的偏值；λi為第i個隱含層節點與輸出節點的連接權值。

1.4 深度極限學習機（DELM）

深度極限學習機（DELM）從結構上看相當于把多個極限學習機（ELM）連接到一起，能更全面地捕捉到數據之間的映射關系，有效提高處理高維度、非線性數據的能力。設DELM 有Q組訓練數據{(xi，yi)|i=1，2，…，Q}和M個隱含層，將輸入訓練數據樣本根據自編碼器極限學習機（ELM-AE）理論得到第一個權值矩陣β1，接著得到隱含層特征向量H1，…，以此類推，能夠得到M層的輸入層權重矩陣βM和隱含層特征向量HM。DELM 數學模型表述式為［15-17］：

式中：L為隱含層神經元個數；Z為隱含層神經元對應的衍生神經元個數；為第j個隱含層神經元對應的第k個衍生神經元與輸出層的權值向量；gjk為第j個隱含層神經元激活函數的k階導函數；n為輸入層神經元個數；為輸入層與第j個隱含層神經元之間的權值向量；bj為第j個隱含層節點的偏置。

1.5 建模流程

WPD-EHO-ELM、WPD-EHO-DELM 模型預報步驟如下：

步驟一：為兼顧模型預報精度和計算規模，本文基于dmey小波包基，采用2 層WPD 將景東水文站2016-2020 年逐日時序數據分解為4 個子序列分量［2，1］～［2，4］；作為對比方法，采用WD 將實例日徑流時序數據分解為4 個子序列分量S1～S4，見圖1、2。

圖1 景東站WPD分解3D效果圖Fig.1 Jingdong Station WPD decomposition 3D renderings

圖2 景東站WD分解3D效果圖Fig.2 Jingdong Station WD decomposition 3D renderings

從圖1、2 可以看出，［2，4］、S4 主要為低頻部分，聚集了原始日徑流時間序列的大部分能量，描述了日徑流序列的趨勢；［2，1］、S1 為所有分解分量中的高頻成分，也是幅值較低的分量，描述了日徑流序列的波動情況。

步驟二：為便于各分量預測結果重構，在延遲時間為1的條件下，采用Cao 方法確定各子序列分量的嵌入維度m，即選取景東水文站前m 天的徑流量來預報當日（1 d）、第二日（2 d）、……、第5日（5 d）的日徑流量。經計算，Cao方法確定子序列分量［2，1］～［2，4］m值分別為13、24、12、13；確定子序列分量S1～S4m值分別為28、24、26、15；確定原日徑流序列m值為25。并選取景東水文站2016-2018年逐日徑流作為訓練樣本，2019-2020年逐日徑流作為預報樣本。

步驟三：利用訓練樣本均方誤差（MSE）作為EHO 優化ELM、DELM輸入層權值和隱含層偏值的適應度函數minf。

步驟四：設置最大迭代次數T，種群規模N；隨機初始化大象位置。

步驟五：計算大象個體的適應度值，確定并保存當前最佳大象位置xbest。令迭代次數t=1。

步驟六：利用式（3）更新種群中大象個體位置；利用式（4）更新當前最優個體位置；利用式（5）更新當前最差個體位置，保留更好個體位置。

步驟七：計算更新之后大象種群個體適應度值，比較并保存當前最佳大象位置xbest。

步驟八：令t=t+1。判斷是否滿足終止條件，若是，輸出xbest，算法結束；否則轉至步驟六。

步驟九：輸出最佳大象位置xbest，xbest即為ELM、DELM 輸入層權值和隱含層偏值最佳矩陣。利用最優ELM、DELM 輸入層權值和隱含層偏值矩陣建立EHO-ELM、EHO-DELM 模型對各分量進行多步預測，將預測結果疊加重構后即得到實例多步日徑流預報結果。

步驟十：利用平均絕對百分比誤差（MAPE）、平均絕對誤差（MAE）、確定性系數（DC）和合格率（PR）對預報模型進行評估，見式（9）。

2 實例應用

景東站位于云南省普洱市景東縣錦屏鎮，建于2000 年1月，系紅河流域李仙江干流控制站，控制徑流面積5 521 km2，水文站至源頭河長90 km，河道坡度6.68‰，為省級重要水文站和省級報汛站。李仙江發源于大理州南澗縣寶華鄉東北部，流經普洱市景東、鎮沅等縣，于普洱市江城縣與紅河州綠春縣的界河流入越南，出境后稱黑水河。李仙江云南境內河道長473 km，落差1 790 m，流域面積19 309 km2，多年平均流量約460 m3/s，主要支流有阿墨江、勐野江、泗南江等。

本文以景東水文站2016-2020 年日徑流預報為研究對象，日徑流變化曲線見圖3。從圖3 可以看出，景東水文站日徑流時序數據呈現出典型的多尺度、高度非線性特征，其最大與最小實測徑流之比高達89.7，起伏變化十分激烈。

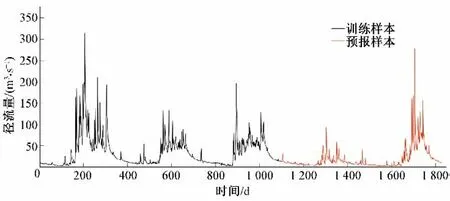
圖3 景東站2016-2020年逐日徑流變化曲線圖Fig.3 Daily runoff change curve of Jingdong Station from 2016 to 2020

2.1 模型參數設置

設置EHO 算法最大迭代次數T=100，種群規模N=50，其他采用算法默認值；ELM 網絡激活函數選擇sigmoid，隱層節點數為2m-1（m為輸入維數），輸入層權值和隱含層偏值搜索空間設置為［-1，1］；DELM 采用3 隱層網絡，隱層節點數為［2m m m］（m為輸入維數），激活函數選擇sigmoid 函數，輸入層權值和隱含層偏值搜索空間設置為［-1，1］；所有模型數據均采用［-1，1］進行歸一化處理。

2.2 預測結果及分析

利用所構建的WPD-EHO-ELM、WPD-EHO-DELM 等6 種模型對景東水文站2016-2020 年日徑流進行訓練及多步預報，結果見表2。并利用上述評估指標對模型性能進行評估。各模型預報相對誤差效果圖見圖4。

依據表1及圖4可以得出以下結論：

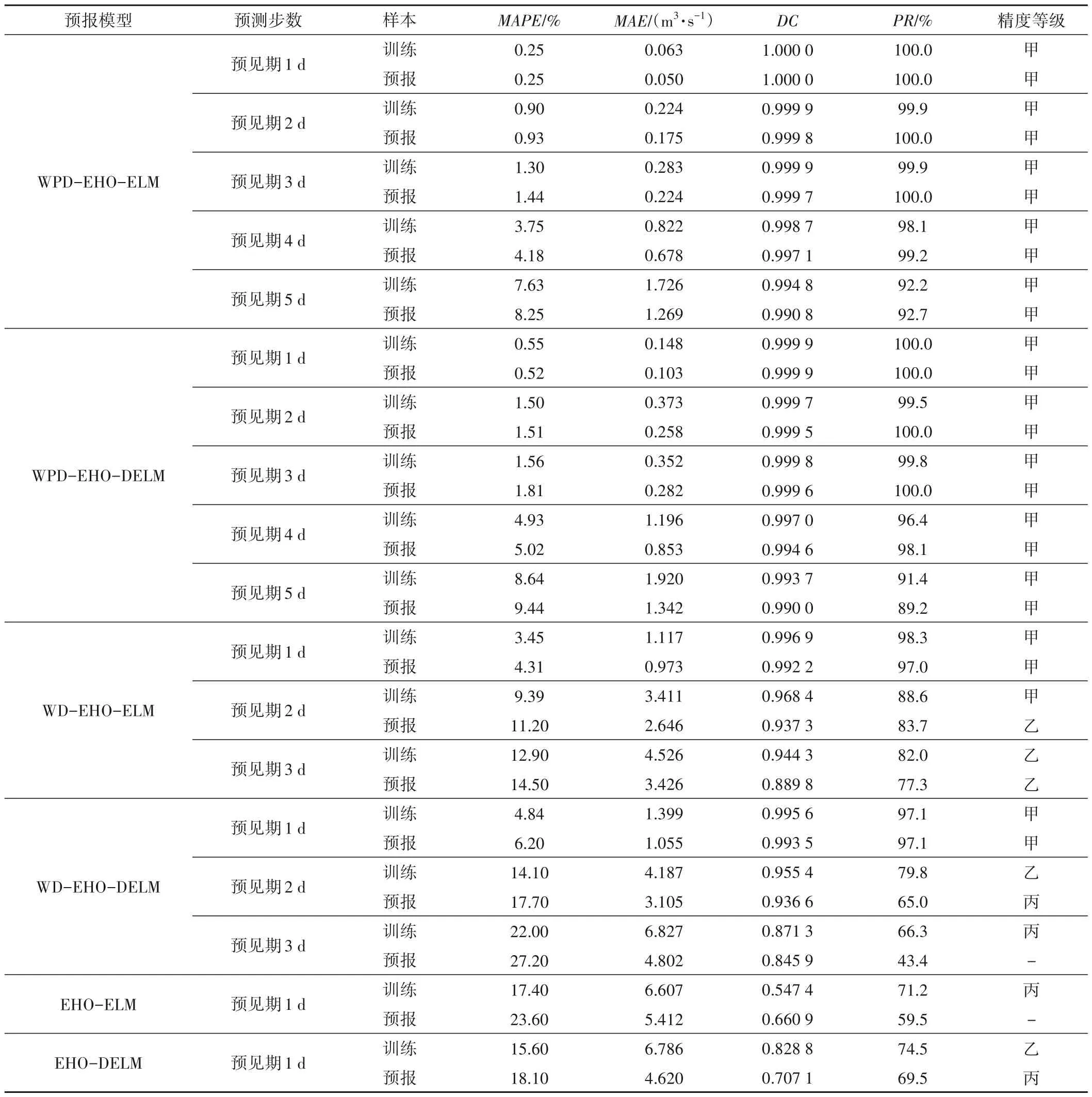
表1 各模型景東站多步預測結果對比Tab.1 Comparison of multi-step prediction results of each model Jingdong Station

（1）WPD-EHO-ELM、WPD-EHO-DELM 模型對景東水文站預見期為1～5 d 日徑流預報的MAPE分別在0.25%～8.25%、0.52%～9.44%之間，MAE在0.050～1.269 m3/s、0.103～-1.342 m3/s之間，PR≥89.2%，DC≥0.990 0，精度評價等級均為甲級（合格率≥85%、確定性系數≥0.90），預報精度優于WD-EHO-ELM 等其他模型。其中預見期為1～3 d 日徑流預報的MAPE≤1.81%、PR 均為100%，DC≥0.999 6，預報效果尤為理想。可見，WPD-EHOELM、WPD-EHO-DELM 模型日徑流多步預報結果可靠性較強，均能夠很好的逼近實測日徑流值，將其用于日徑流時間序列多步預報是可行和可靠的。相對而言，WPD-EHO-ELM 模型預報效果略優于WPD-EHO-DELM 模型。

（2）從基于WPD、WD 方法構建的不同模型預報效果來看，WPD-EHO-ELM、WPD-EHO-DELM 模型預報精度優于WDEHO-ELM、WD-EHO-DELM 模型，表明WPD 能充分挖掘日徑流時序數據的潛藏規律，同時將低頻、高頻信號進行再次分解，提取出更具規律的子序列分量，其分解效果要優于WD方法。

（3）從WPD-EHO-ELM、WPD-EHO-DELM 兩種模型預報效果對比來看，雖然DELM 相當于把多個ELM 連接到一起，能更全面地捕捉到數據之間的映射關系，但過多的ELM 組合不但增加模型復雜度，同時也增加優化DELM 輸入層權值和隱含層偏值的難度；ELM 雖然只有1 個隱層，但通過EHO 算法優化獲得最佳ELM 輸入層權值和隱含層偏值，同樣可以獲得理想的預報效果。

（4）WD-EHO-ELM、WD-EHO-DELM 模型僅在單步預報情形下（預見期為1 d）能達到《水文情報預報規范》（GB/T22482-2008）預報精度等級甲級；在預見期為2 d情形下，WDEHO-ELM 模型預報精度等級為乙級，WD-EHO-DELM 模型為丙級；在預見期為3 d 情形下，WD-EHO-ELM 模型預報精度等級為乙級，WD-EHO-DELM 模型已不能滿足預報精度要求。在日徑流時序數據未經分解情形下，即便在預見期為2 d 情形下，EHO-ELM、EHO-DELM 模型預報精度均不理想，僅EHODELM模型預報精度等級達到丙級，EHO-ELM 模型已不能滿足預報精度要求。

（5）從圖4 可以看出，WPD-EHO-ELM、WPD-EHO-DELM模型對景東水文站預見期為1～3 d 絕大多數日徑流預報的相對誤差均在-2%～2%范圍內波動，具有更小的預報誤差和更高的預報精度。

圖4 各模型預報相對誤差3D效果圖Fig.4 3D rendering of the relative error of each model forecast

3 結論

為提高日徑流時間序列多步預報精度，基于WPD 方法、EHO 算法和ELM、DELM 網絡，研究提出WPD-EHO-ELM、WPD-EHO-DELM 日徑流時間序列多步預報模型，并構建WDEHO-ELM、WD-EHO-DELM、EHO-ELM、EHO-DELM 作對比分析模型，通過云南省景東水文站日徑流時間序列多步預報實例對各模型進行驗證，得到如下結論：

（1）WPD-EHO-ELM、WPD-EHO-DELM 模型對景東水文站預見期為1～5 d日徑流預報均達到《水文情報預報規范》（GB/T22482-2008）預報精度等級甲級，預報效果優于其他對比模型。其中，預見期為1～3 d日徑流預報的MAPE≤1.81%、PR均達100%，DC≥0.999 6，預報效果最理想。可見，將WPD-EHOELM、WPD-EHO-DELM 模型用于日徑流時間序列多步預報是可行、可靠的。模型及方法可為實現日徑流時間序列精準預報提供新的途徑。

（2）WPD-EHO-ELM、WPD-EHO-DELM 模型預報精度優于WD-EHO-ELM、WD-EHO-DELM 模型，表明WPD 能充分挖掘日徑流時序數據的潛藏規律，同時將低頻、高頻信號進行再次分解，提取出更具規律的子序列分量，其分解效果要優于WD方法。

（3）相較于WPD-EHO-DELM 模型，WPD-EHO-ELM 模型表現出更簡潔、更高效的預報效果。雖然DELM 能更全面地捕捉到數據之間的映射關系，但過多的ELM 組合不但增加模型復雜度，同時也增加EHO 算法優化DELM 輸入層權值和隱含層偏值的難度；雖然ELM 網絡僅有1 個隱層，但通過EHO 算法優化獲得最佳ELM 輸入層權值和隱含層偏值，同樣可以獲得更好的預報效果。

（4）WPD-EHO-ELM、WPD-EHO-DELM 模型能充分發揮WPD 方法、EHO 算法和ELM、DELM 網絡優勢，表現出較好的預報精度和穩定性能，模型的預報精度隨著預見期天數的增加而降低。