排球平拋運動的臨界模型

康寶龍

(甘肅省合水縣第一中學)

在學習平拋運動時,我們經常碰到以排球做平拋運動為背景的習題,其中排球的兩類臨界問題是平拋運動學習的難點.下面我們就對這兩類臨界問題加以例析總結,以期讀者能更好地突破該難點.

1 臨界速度的計算——球既不觸網又不出界

如圖1所示,擊球高度為h1,球網高度為h2,擊球點到球網及球網到邊線的水平距離分別為s1和s2,要使球既不觸網又不出界,求水平有效擊球的速度范圍.

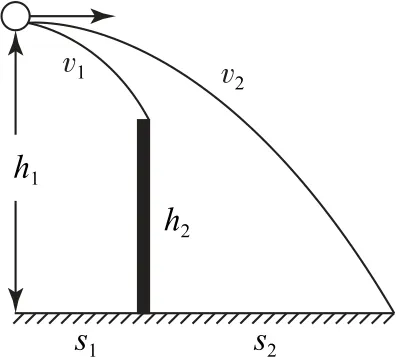
圖1

1)從網上擦過的臨界速度v1的大小計算.水平方向s1＝v1t1,豎直 方向h1－h2＝.兩式聯立解得v1＝s1

在高度h1處有效發球的速度范圍是

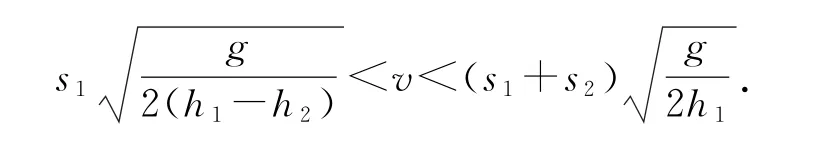
例1如圖2所示,某學校的排球場長為18m,球網高度為2 m.一同學站在離網3 m 線上(虛線所示)正對網豎直跳起,并在離地高2.5 m 處將球向正前方水平擊出.不計球飛行過程中受到的阻力,g取10m·s－2,欲使球既不觸網又不出界,則擊球速度可能是().

圖2

2 臨界高度的計算——球不是觸網就是出界

如圖3所示,當擊球點的高度h1為何值時,無論水平擊球的速度多大,球不是觸網就是出界.

圖3

例2如圖4所示,排球場總長為18m,設網的高度為2 m,運動員站在離網3 m 遠的線上正對網前豎直跳起,在高為2.5 m 處把作為質點的排球垂直于網水平擊出.(空氣阻力不計,重力加速度g取10m·s－2)則().

圖4

B.擊球速度大于20m·s－1,球必定會出界

C.擊球速度小于10m·s－1,球必定會觸網

D.只要擊球點高于2m,且擊球速度合適,球總可以落到對方界內

解析如圖5所示,排球恰好不觸網時其運動軌跡為Ⅰ.排球恰好不出界時其運動軌跡為Ⅱ,根據平拋運動的規律,排球恰好不觸網時有x1＝3m＝v1t1,h1＝2.5m－2m＝,解得排球飛行時間·s－1≈9.5m·s－1.

圖5

當排球恰好不出界時有x2＝3 m＋9 m＝v2t2.h＝2.5 m ＝,可解得m·s－1≈17m·s－1,故選項A、B正確,選項C錯誤.

如圖6所示為排球恰好不觸網也恰好不出界的臨界軌跡.設擊球點高度為h,根據平拋運動的規律有

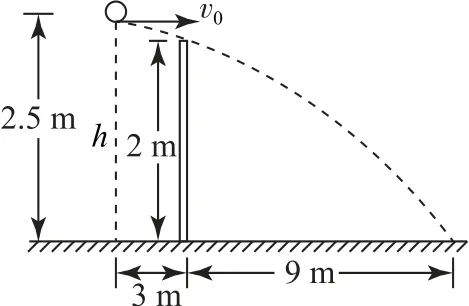
圖6

聯立以上四式可得h＝2.13m,故選項D 錯誤.

例3如圖7所示是排球場地的示意圖.排球場ABCD為矩形,長邊AD＝L＝18 m,前場區的長度為,寬L2＝12m,網高為h＝1.95m.在某次排球比賽中,若運動員在底線AB中點P的正上方跳起水平發球,當排球進入對方半場的后場區域時才算有效,忽略空氣阻力,排球可看作質點,下列說法正確的是().

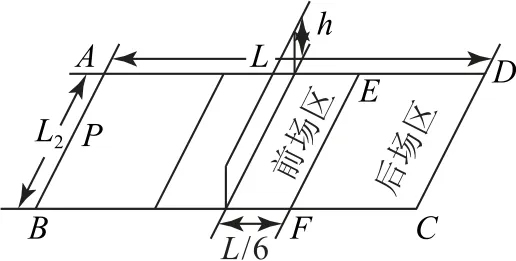
圖7

A.若運動員的擊球點高度為3.20m,有效擊球的最小速度為18m·s－1

B.若運動員的擊球點高度為3.20 m,有效擊球的最大速度為22.5m·s－1

C.若沿垂直AB方向水平擊球,擊球點高度小于2.6m,則發球必定失敗

D.若沿PD方向水平擊球,擊球點高度高于2.6m,只要速度合適,發球可以成功

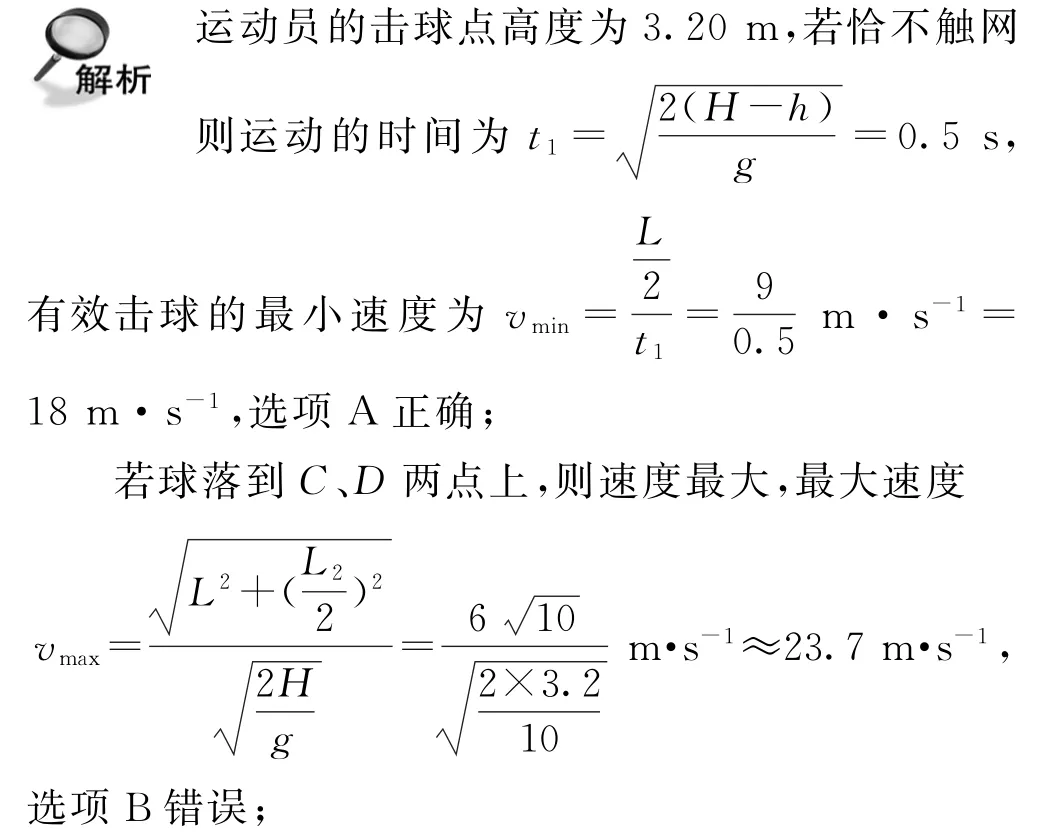
若沿垂直AB方向水平擊球,打到觸網點與打到CD線時間之比為1∶2,則下落高度之比為1∶4,所以臨界高度與網高比為4∶3,則臨界高度為H0＝＝2.6m.則若沿垂直AB方向水平擊球,擊球點高度小于2.6m,發球一定會失敗,選項C正確;

若沿PD方向水平擊球,擊球點高度大于2.6m,只要速度合適,發球可以成功,選項D 正確.

總之,在解答排球類試題的兩類臨界問題時,首先確定題目是臨界速度問題,還是臨界高度問題,然后畫出排球的臨界軌跡,根據臨界軌跡,列出水平方向和豎直方向的方程,消去時間“t”,即可求解.

(完)