銅合金空洞缺陷形變演化研究探討*

劉勁松，李 旺，陳帥峰，陳大勇,，王松偉，李慶文，鄭佳依

（1.沈陽理工大學材料科學與工程學院，遼寧 沈陽 110159；2.中國科學院金屬研究所，師昌緒先進材料創新中心，遼寧沈陽 110016；3.常州潤來科技有限公司，江蘇 常州 213149）

1 引言

銅及其合金因導電、導熱性能優異，在電力裝備、交通運輸、建筑和家用電器等領域得到廣泛應用。進入消費終端之前，銅及其合金通常被制成各種截面形狀的加工材，其中銅桿線材、銅板帶材及銅管材產量占比最大。銅加工材生產工藝以“連續鑄造+多道次軋/拉”最為廣泛［1］，這一工藝具有短流程、低成本的優勢［2］，然而成品率受鑄坯質量影響較大。鑄坯凝固過程中其內部常產生氣泡、縮孔等空洞缺陷［3-7］，并且這些空洞缺陷，在生產中只能盡量抑制，難以完全避免。后續加工過程中，空洞缺陷常演變為內部裂紋或表面缺陷，降低了成品率。借助加工過程中的熱擴散和再結晶［8］，空洞缺陷在合適的變形量和變形溫度下可以閉合并進一步焊合修復，為消除鑄坯缺陷創造了可能。

鑄坯空洞缺陷的形變閉合是焊合修復的先決條件，其形變演化預測對于后續加工具有重要指導意義。因此，有必要開展這方面的研究工作。金屬空洞缺陷形變演化的現有研究成果可分為模擬研究、唯象模型研究、細觀模型研究。模擬研究以物理模擬或數值模擬為研究手段，通過在試件或有限元模型中人為設置缺陷并模擬實際缺陷的閉合過程，得到關于缺陷閉合規律的定性認識或簡單的閉合判據［9-19］；唯象模型研究基于實驗觀測和理論猜想建立數學模型，經過參數擬合及修正，得到適用于特定工藝及特定缺陷形態的唯象模型［20-26］；細觀模型研究基于細觀力學分析建立缺陷演化的解析模型，模型通常適用于更為一般的缺陷初始狀態，具有更高的預測精度［27-31］。鑒于現有研究對于銅合金關注較少，本文對某錫磷青銅連鑄板坯的內部空洞缺陷及鑄態組織進行了觀察，討論了現有研究成果對于銅合金的適用性；針對當前研究在幾何建模方面的難點，采用Python語言設計了含任意橢球空洞的體元模型自動建模程序。還原實際成形過程。物理模擬中，常用作模擬材料的有軟鋼、塑泥和鉛［9-11］，也有的采用鋁、石蠟和聚氨酯等［12,13］。模擬方法主要有網格法、硬度法、低倍顯微組織法、光塑性法和密柵云紋法等。

Chaaban等［9］研究了預制圓柱空洞的鉛試件在不同空洞參數及變形參數下拔長時的空洞閉合規律，發現縱向空洞的閉合效率大于橫向空洞的閉合效率，而且空洞內壁貼合后必須繼續施壓才能使其焊合。謝冰等［10］采用鉛作為模擬材料研究了大型軸類鍛件寬砧鍛造時的空洞閉合規律，發現砧寬比越大，空洞閉合所需的臨界壓下量越小；已閉合的空洞在試件翻轉90°繼續鍛壓時仍有可能再次張開，經多道次拔長后則基本保持閉合。渡邊誠等［11］采用白塑泥作為模擬材料，研究了鋼錠鍛壓過程中的變形、應力、壓機載荷及空洞閉合規律，定性得到了空洞壓實的應力應變條件；通過工藝實驗，證明了使用FM法（無曼內斯曼效應鍛造法）和FML法（低載荷FM鍛造法）能有效壓實大鋼錠內部的空洞缺陷。蔣智等［12］采用聚碳酸酯作為模擬材料（圖1），對含有球形空洞的圓柱體鍛件鐓粗變形過程進行了光塑性模擬，發現越接近圓柱體表面的空洞越難閉合，空洞位于圓柱體中心時最容易閉合。王祖唐等［13］采用45#鋼作為模擬材料，研究了不同應變狀態下的空洞閉合效率，發現對于平面應變壓縮變形，圓柱形空洞的軸線和試件展寬方向垂直時空洞閉合效率最高；自由鐓粗時空洞閉合效率最低。

圖1 含球形空洞的聚碳酸酯試件

2 模擬研究

物理模擬是最早用于金屬塑性加工問題的研究手段，在高性能電子計算機尚未普及的時代，物理模擬是替代工藝實驗的最佳選擇，可在一定程度上

物理模擬具有簡便、直觀的優點，因而得到廣泛應用，但其與實際加工過程的材料本構和邊界條件相差甚遠，結果誤差較大。此外，當模擬數量較大時，物理模擬的工作周期較長、成本較高。隨著計算機運算能力的不斷提高，采用數值模擬方法求解彈塑性力學問題更加高效，數值模擬逐漸成為塑性加工問題的常規研究手段。

Dudra等［14］采用數值模擬方法研究了自由鍛過程中的空洞閉合，并通過實驗驗證了數值模擬結果的準確性。模擬結果表明，等效應變和靜水應力對空洞閉合具有主要貢獻，但等效應變與空洞主應變之間的關聯系數更大，是更好的閉合指標。熱鍛過程中，由于坯料表面冷卻的影響導致坯料內部產生溫度梯度，O¨verstam等［15］采用數值模擬方法研究了坯料內部溫度梯度對缺陷閉合的影響。研究發現，表面冷卻有利于坯料內部的缺陷閉合，且鍛件尺寸越小表面冷卻的影響越顯著。Chun等［16］采用數值模擬方法研究了拔長鍛造過程中成形力及缺陷閉合效率與道次參數設計及壓頭尺寸之間的關系，研究結果表明：較小的壓頭圓角半徑以及壓頭斜角有利于缺陷閉合，但成形力也隨之增大；對于多道次拔長鍛造，缺陷閉合主要發生在第一道次，后續道次中缺陷體積變化較小。崔振山等［17］采用數值模擬方法研究了內部含有空洞的圓柱體鍛件熱鐓粗過程，分析了空洞附近的應力應變特點以及影響空洞閉合的各種因素。模擬結果表明，變形過程中空洞邊緣微小區域內會產生雙向拉應力，直到空洞閉合時拉應力才會變成壓應力；壓下方向的應變絕對值最大，主導著空洞的閉合過程。Llanos等［18］采用數值模擬方法研究了鑄軋型材的芯部質量控制，發現軋件中的自然缺陷相比人工缺陷更難閉合，這一發現與Chen K等［19］的研究結果一致。Chen K等［19］采用數值模擬方法研究了含不同形狀缺陷的圓柱體鐓粗變形過程，發現缺陷形狀越復雜，對應的缺陷閉合臨界壓下率越大，也即閉合難度越大（圖2）。

圖2 不同形狀缺陷的圓柱鐓粗閉合臨界壓下率對比

關于金屬空洞缺陷閉合問題，國內外研究者通過模擬研究得出了許多有價值的結論，一般性地歸納如下：1）大塑性變形有利于缺陷閉合，但缺陷閉合后期其體積減小的難度急劇增大，此時必須借助高溫下的擴散和再結晶進一步修復缺陷；2）變形路徑顯著影響缺陷的閉合效率，已閉合缺陷在基體繼續變形過程中仍有可能再次張開；3）合理選用成形工具可有效提高缺陷的閉合效率，例如在鋼錠開坯鍛中使用型砧代替平砧、在厚板軋制中使用較大直徑的軋輥；4）摩擦系數、溫度梯度等邊界條件顯著影響坯料變形均勻性，進而影響缺陷閉合；5）同一變形條件下，缺陷的初始幾何狀態（形狀、尺寸、位向、所處位置）決定其閉合難易程度。

3 唯象模型研究

鑒于空洞閉合是一個連續漸進的過程，Tanaka等［20］提出將靜水積分Gm作為缺陷閉合判據，引入了等效應變這個累積量。Gm定義如下：

式中，σm為靜水應力，σe為等效應力，εe為等效應變。Nakasaki等［21］將Gm作為熱軋過程的缺陷閉合判據，根據實驗結果將Gm的值修正為

孫捷先等［22］認為，僅通過應力應變來評估缺陷閉合程度，往往會得出相互矛盾的結論。認為缺陷閉合是變應力狀態下變形的累積過程，僅由一時的應力應變無法得出正確結論，于是提出用鍛合能指標E來評估缺陷閉合程度：

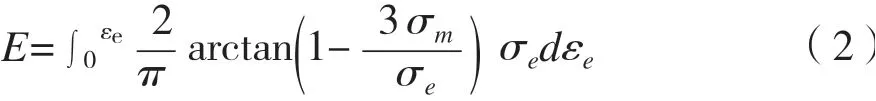
E值作為缺陷閉合判據與Tanaka等［20］提出的靜水積分判據并無本質上的不同，E值與空洞閉合程度之間的定量聯系并不明確。

Chen等［23］通過引入靜水積分的三軸推廣形式Gi(i=x,y,z)，建立了一種能夠描述空洞三維形狀及其尺寸變化的幾何演化模型：

式中，Si=2Ri/(Rj+Rk) 為空洞形狀參數，Si0為Si的初始值；Ri為i方向上的空洞半徑；si是偏應力張量的主軸分量；C1、C2、C3為擬合系數。當Si=0 時，表明空洞完全閉合。該模型假設空洞初始形狀為正

交橢球形（圖3），使其能夠對實際缺陷進行更加精確的幾何近似，從而提高缺陷形變演化的預測精度，但該模型無法描述缺陷的轉動。

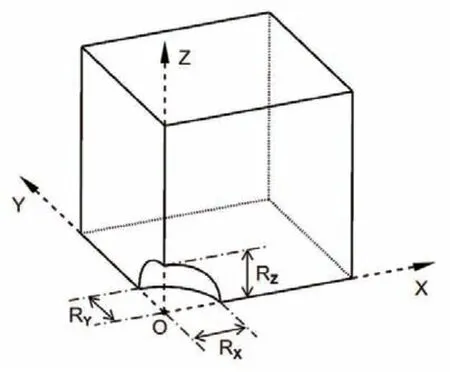
圖3 正交橢球形空洞示意圖（1/8對稱）

崔振山等［24］采用數值模擬方法，分析了含軸對稱橢球形空洞的圓柱體鍛件熱鐓粗過程，發現鍛件的高徑比、空洞形狀、摩擦條件是空洞閉合的主要影響因素，而變形溫度、壓下速度、空洞尺寸等因素對空洞閉合影響較小。基于數值模擬結果，通過多維變量非線性擬合，得到了空洞閉合的臨界壓下率計算公式：

式中，H/D為圓柱坯料高徑比，a、b為橢球形空洞的長短軸半徑，m為剪切摩擦系數，Rd為空洞閉合的臨界壓下率。該公式的預測結果與有限元模擬結果吻合良好，一定程度上反映了各主要影響因素對空洞閉合的影響規律。

文新理等［25］研究了 27SiMn 鋼軋制過程中的空洞型缺陷演變規律，認為變形量是軋制過程中影響空洞閉合的主要因素，建立了空洞平均直徑與變形量間的數學關系（式5-a），并通過一元非線性回歸得到了參數A、B、C的值（式5-b）：

式中，D為空洞平均直徑，ε為板材軋制壓下率。該模型與崔振山等［24］提出的模型本質相同，雖然其形式簡單且與實驗結果吻合良好，但局限于具體工藝，難以推廣應用。

Saby等［26］以一個包含任意橢球形空洞的體元模型（圖4）作為基本幾何模型，通過大量而系統的數值模擬工作，研究了幾何、材料、載荷因素對空洞閉合的影響。根據模擬結果表現出的規律，建立了式6所示的數學模型（其中B、C是關于空洞初始幾何及應力狀態的函數），并利用模擬結果回歸得到了各模型參數。模型充分考慮了缺陷閉合的各種影響因素，數學形式構造得當，表現出較高的預測精度。模型未考慮材料本構差異，但由于其建模流程固定且數學形式簡潔，對于不同材料完全可以通過同一套流程獲得其對應的模型參數。模型考慮了橢球空洞的初始位向及初始尺寸，但未考慮空洞幾何在變形過程中的實時變化帶來的影響。

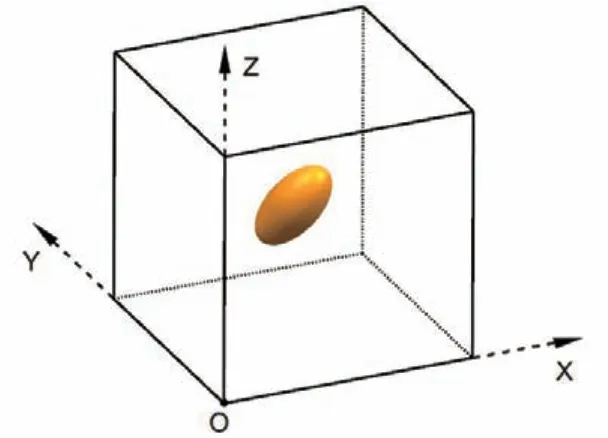
圖4 含任意橢球形空洞的體元模型

4 細觀模型研究

Eshelby［32］在上世紀50年代提出了等效夾雜方法，推導出了全空間中橢球夾雜體包含均勻本征應變的理論彈性解，他的開拓性工作極大促進了細觀力學夾雜問題的研究進展［33］。由于夾雜體與基體材料模量的差異而產生的基體應力場擾動，可以由夾雜體中適當分布的等效本征應變來模擬，而把夾雜體視為與基體完全相同的材料，這就是Eshelby等效夾雜法。Mura在他的《Micromechanics of defects in solids》一書中將一般語境下的“夾雜（inclusions）”一詞賦予了特殊的含義［34］，另外又定義了“雜質（Inhomogeneities）”一詞。按照Mura的定義：“包含雜質的材料其內部不存在任何應力場，除非對該材料施加外載荷；包含夾雜的材料其內部存在一個內應力（本征應力）場，即便該材料不受任何外載荷［34］”，故金屬材料的內部空洞缺陷可按“雜質”處理。

劉熠等［35］討論了非線性基體中 Eshelby 等效夾雜方法的適用性問題，并給出了非線性基體中遠場球對稱應力作用下單個球形空洞的幾何演化問題精確解。研究結果表明，Eshelby 等效夾雜方法不能簡單地推廣應用于非線性基體中空洞幾何演化的力學分析。

Budiansky等［36］將Eshelby的理論推廣應用于線性黏塑性材料中軸對稱橢球空洞的幾何演化分析，馮超［31］基于該理論研究了線性黏塑性材料中任意橢球形空洞的演化行為，發現空洞在某一主軸方向的變形主要受到平均應力及該主軸方向偏應力的影響，而對其他方向的偏應力并不敏感，據此得到了空洞半徑應變率的近似表達式。采用數值模擬方法研究了不同應力邊界條件下不同形狀空洞的演化行為，發現在應力三軸度絕對值小于1的載荷條件下，非線性黏塑性材料與線性黏塑性材料的空洞演化規律類似。據此仿照線性黏塑性材料情形提出了適用于非線性黏塑性材料的空洞半徑應變率表達式：式中，為空洞某一主軸的應變速率，Ri為空洞半徑，為空洞半徑變化速率，σe為等效應力，為等效應變速率，′為偏應力，σm為平均應力。

式7中，Mi、Ni是與空洞形狀有關的系數。馮超［31］采用數值模擬方法計算了包含不同形狀空洞的體元模型，獲得了應力三軸度絕對值小于1的載荷條件下的一系列Hi值，通過參數擬合得到了Mi、Ni關于空洞半徑Ri的表達式。將前人研究和有限元模擬結果的對比驗證了模型的準確性。

Gurson在20世紀70年代建立了一套比較完備的本構理論，用以描述內部空洞對材料塑性行為的影響［37］。Gurson假設金屬材料內部含有球形空洞，以圖5所示的胞元為基本力學模型，分析了材料的變形及斷裂過程并提出了多孔材料的屈服函數模型（Gurson模型）：

圖5 含同心球形空洞的球形胞元

Gurson模型表征了各向同性的損傷演化過程，引入的損傷變量f反映了空洞體積變化，且當f值較小時，材料變形過程中空洞形狀改變帶來的影響可以忽略不計［27］。

為考慮塑性變形過程中的材料硬化，提高模型預測精度，Tvergaard向Gurson模型中引入了3個修正系數，提出了著名的Gurson-Tvergaard（G-T）模型（式10）［39］。基于G-T模型導出的球形空洞體積應變率［40］見式11-a，對該式進行積分，即可得到式11-b所示的空洞體積演化方程。當q1=q2=1時，式11-a與Gurson模型導出的空洞體積應變率相同。Tvergaard借助數值模擬方法研究了空洞長大過程，發現當q1=1.5，q2=1.0時式11-a的預測結果與模擬結果吻合良好［39］。

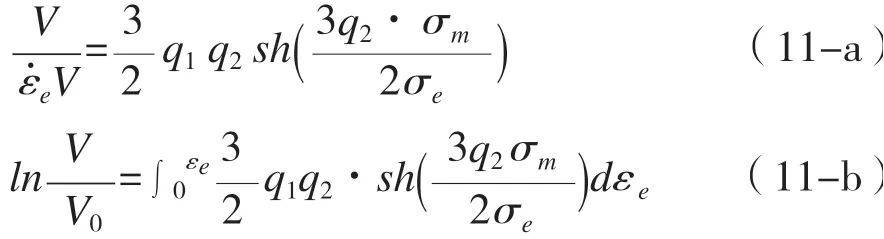
朱明等［27］基于Gurson模型從理論上分析了空洞閉合過程，通過引入空洞形狀改變因子對Gurson模型進行了修正，得到了與G-T模型等價的修正模型。該研究提出了一種有限體積的橢球胞元中包含橢球形空洞的細觀模型，并導出了該模型在橢球—雙曲旋轉面坐標系下的運動學許可速度場，為后續研究者建立考慮空洞形狀變化和主軸轉動的空洞演化模型建立了一定基礎。

為了提高G-T模型對空洞閉合過程中空洞體積的預測精度，李妍等［28］以數值模擬作為試驗手段，通過正交試驗對G-T模型進行了系數尋優，找到了式10中修正系數的最佳值。研究結果表明，對于空洞閉合過程中空洞體積的預測，G-T模型中修正系數的最佳取值為：q1=6.0，q2=2.5，q3=0.5。采用最佳修正系數，G-T模型預測結果與數值模擬結果吻合良好。

Afshan等［29］開發了一套基于模式搜索方法的參數尋優計算程序，用以提高G-T模型參數校核效率，同時探究了G-T模型對空洞閉合問題的適用性。采用由上述參數尋優計算程序得到的q參數時，G-T模型預測與數值模擬結果的吻合度大幅提高，表明了該參數尋優計算程序的有效性，同時也證明了G-T模型對空洞閉合問題的適用性。

Lee和Mear的研究表明，空洞的初始形狀對于其形變閉合有著顯著影響［41］。大量的模擬研究發現：在低應力三軸度及大變形的閉合條件下，空洞的形狀改變尤為明顯。Gurson類模型具有簡潔實用的優點，然而模型假設空洞初始形狀為球形且空洞在閉合過程中保持球形，降低了模型預測精度。

5 錫磷青銅連鑄板坯內部空洞缺陷

為了考察現有研究成果對于銅合金的適用性，對某牌號錫磷青銅連鑄板坯的內部空洞缺陷進行了剖切觀察。通過超聲探傷確定了空洞缺陷在板坯中的位置，在含缺陷位置進行取樣并對樣品進行剖切、打磨，獲得了空洞缺陷的顯微照片，圖6列出了其中有代表性的一部分。觀察到的缺陷形狀主要有：等軸狀［圖6（c）、（d）、（f）］、短棒狀［圖6（a）］、蠕蟲狀［（圖6（b）］、其他不規則形狀［（圖6（e）］。觀察到的缺陷內壁形貌有光滑［圖6（c）］和粗糙（其他）兩種；觀察到的空洞缺陷截面尺寸從10μm到250μm不等。

雖然觀察到的鑄坯空洞缺陷尺寸小至10微米，但在基體材料均勻連續的假設下，現有研究成果仍然適用。圖7是連鑄板坯的金相照片，可見晶粒尺寸遠大于圖6所示的空洞缺陷尺寸，即當前觀察到的空洞缺陷已經達到了鑄坯晶粒的更小尺度，基體材料均勻連續的假設顯然不夠精確。鑄坯凝固過程中，空洞缺陷可能在晶內產生，也可能在晶界產生，晶內和晶界處的不同變形特性可能對應著顯著不同的缺陷演化特性。與此同時，不同晶粒的晶體學取向存在差異，力學性能的微觀各向異性也可能對缺陷演化產生影響。鑒于此，有必要進一步研究材料微觀結構對銅合金空洞缺陷形變演化的影響，并相應地開發缺陷演化建模系統、建立缺陷演化數學模型。

圖6 錫磷青銅連鑄板坯的內部空洞缺陷

圖7 錫磷青銅連鑄板坯金相

基于上述實驗觀測，發現連鑄板坯的內部空洞缺陷可以由任意橢球形近似描述（圖4）。任意橢球形作為空洞缺陷的幾何近似，一方面便于對空洞缺陷的形變演化進行數值模擬及數學解析，另一方面也可實現較高的幾何近似精度。空洞缺陷的形變演化研究需要大量創建具有隨機參數的橢球空洞數字模型。為了降低建模難度、提高建模效率，采用Python語言設計了含任意橢球空洞的體元模型自動建模程序。

自動建模程序生成的體元模型如圖8所示，工作原理如圖9所示。程序開始執行后，自動導入指定路徑下用戶預先寫好的控制參數文件，根據控制參數生成包含任意橢球空洞的體元模型，最后自動輸出模型文件到指定路徑。程序的核心功能包括：1）塊體尺寸及橢球空洞的數量可在控制參數文件中設定；2）橢球空洞的位向在程序執行過程中隨機生成；3）橢球空洞的中心坐標和半軸長在約束區間內隨機生成，約束區間可在控制參數文件中設定；4）相鄰橢球空洞的最小間距、橢球空洞與塊體邊界的最小間距可在控制參數文件中設定。該程序可獨立使用，也可作為后續研究計劃中缺陷演化建模系統的一個模塊，具有較高的使用靈活性。

圖8 含任意橢球空洞的體元模型

圖9 含任意橢球空洞的體元模型自動建模程序流程圖

6 結束語

金屬空洞缺陷形變演化問題的研究已有幾十年歷史，然而現有研究對于銅合金缺陷形變演化研究具有重要參考價值，銅合金缺陷形變演化及其受材料微觀結構影響等問題的研究仍有待進一步深入研究。通過對某牌號錫磷青銅連鑄板坯剖切觀察，發現其內部空洞缺陷可以由任意橢球形近似描述，而采用Python語言設計的自動建模程序顯著提高了體元模型建模效率，顯示出計算機編程及軟件等二次開發技術用于研究當前問題的巨大潛力。同時，結合近年來迅猛發展的機器學習等先進信息技術，有望開發出高度自動化的、適用于銅合金乃至更廣泛合金品種的空洞缺陷形變演化建模方案。