基于模糊物元分析的PSO-LSSVM磨加工補調值在線預測與補償方法

張志永，鄭鵬

(1.鄭州科技學院機械工程學院，河南鄭州 450064；2.鄭州大學機械與動力工程學院，河南鄭州 450001)

0 前言

磨削是機械加工中重要的加工方式，磨削精度的高低決定了工件質量的優劣。磨加工主動測量儀是一種能夠實時檢測工件尺寸，廣泛應用于自動、半自動磨床的儀器，其工作原理如圖1所示。

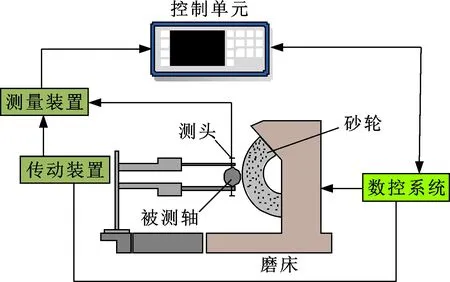
圖1 磨加工主動量儀工作原理示意

在磨削過程中，溫度產生的溫漂會導致系統控制出現偏差,主動測量控制儀動態測量工件也導致偏差的產生；在光磨階段，光磨余量、砂輪轉速、工件轉速的設置也會導致偏差的產生。生產現場操作者針對此類偏差，多采用氣動量儀測量工件得出偏差值，然后對磨削控制系統信號點設置進行補調，手動輸入補調量。此種補調方式滯后于磨削加工進程，且隨意性大，主要依賴于操作者的經驗。因此在不同批次、大批量的流水線生產過程中依然無法滿足自動化的要求。傳統的時序預測方法如小波分析、LSTM等因運算過程復雜、預測精度不足等原因，無法滿足在線測量的要求。因此，需要尋找更加準確高效的預測方式來提高在線測量磨削過程中的加工精度和加工效率。

磨削工藝參數組合優化對于提高產品加工精度和生產效率至關重要，可利用模糊物元描述方式對磨削工藝參數組合進行快速有效地優化。SUYKENS等利用具有等式約束并滿足KKT條件的規則化最小二乘支持向量機函數作為損失函數，提出了最小二乘支持向量機(Least Squares Support Vector Machines, LSSVM)模型，它具有良好的泛化性能、高計算效率和高維魯棒性的優點。將模糊物元分析方法與LSSVM相結合，通過模糊物元分析迅速準確地獲得最佳工藝參數，并將對應的參數作為輸入訓練出LSSVM預測模型。粒子群算法(Particle Swarm Optimization, PSO)是一種源于復雜適應系統的進化算法，從隨機解出發，通過不斷的迭代來尋找最優解，通過適應度函數來評價解的優劣，具有原理簡單、易實現、精度高、收斂快等特點。雖然LSSVM算法具有良好的線性回歸擬合和統計預測能力，但在計算過程中容易陷入局部最優解，使得LSSVM算法的線性回歸和統計預測能力受到影響。因此利用PSO對預測模型進行參數尋優，在保證模型準確率的同時，可提升模型的泛化程度。補調值預測補償反饋控制示意如圖2所示。

圖2 補調值預測與補償反饋控制示意

1 基于模糊物元分析的PSO-LSSVM補調值在線預測模型

1.1 模糊物元分析

物元分析理論中要求用“事物、特征和量值”對事物屬性進行描述。若模型中的量值具有不確定性，可稱為模糊物元，若有個事物、、…、,用其共同的個特征、、…、及其相應的量值1、2、…、，則稱為個事物維復合物元。一般計算中，可用量值代替模糊量值，構成復合模糊物元，記為。

(1)

利用模糊物元描述方式，并使用模糊集合和關聯度評定的方法，將灰色關聯法計算所得的客觀權重和層次分析法所得的主觀權重進行復合，兼顧實驗數據邏輯性和決策可參與性，可很好避免權重分配不合理之處。將2種改進方法結合，可實現對磨削工藝參數組合進行快速有效的優化。

1.2 PSO-LSSVM預測模型構建

設粒子群大小為，單個粒子維數為，即對維空間(1,2,3,…,)進行搜索，表示第個粒子。第個粒子的速度可表示為=(1,2,3,…,)(=1,2,…,)；第個粒子的歷史最優解為=(1,2,3,…,)(=1,2,…,)；粒子群的全局最優值為=(,,,…,g)。其速度和位置更新公式為

(2)

其中：為慣性權重，是用于保持原速度的系數；、分別為個體最優值的權重系數和群體最優值的權重系數，通常都設置為2；、都是[0,1]區間內的隨機數；系數稱為約束因子，通常設置為1。適應度函數是度量粒子當前位置與全局最優位置之間距離的函數，文中將磨加工補調值預測值的均方根誤差作為各個粒子的適應度函數，距離全局最優位置越近的粒子，其適應度函數值越小。適應度函數的表達式為

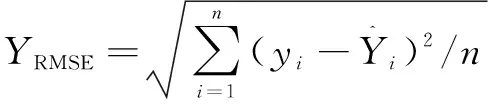
圖3 LSSVM分類和回歸示意

假設樣本集={(,),=1,2,…,}，對于LSSVM，(,)是樣本的輸入和輸出變量，∈,∈。存在一超平面·()+=0，這個超平面可以將所有樣本分開。LSSVM的分類和回歸模型如圖3所示，是超平面的法向量，是其中常數。補調值的預測是非線性問題，需要通過一個核函數將輸入向量從低維空間映射到高維特征向量空間，轉換為線性可分的數據。在高維特征空間對數據構造分類超平面，將映射為高維空間的()，即→()=[(),(),…，()]，根據希爾伯特-施密特原理，將原來線性情況下的內積運算替換成()·()即可。LSSVM利用()=·()+進行估計，式中(·)將輸入從低維非線性映射為高維線性，把非線性問題轉化為高維特征空間中的線性擬和問題。LSSVM的優化問題為式(3)，其中為懲罰參數，決定了函數的光滑程度。

(3)

約束條件公式如下：

[·()+]=1-=1,2,…,

(4)

構造拉格朗日函數進行求解：

(5)

其中，為拉格朗日乘子。根據KKT條件，得到如下等式約束條件：

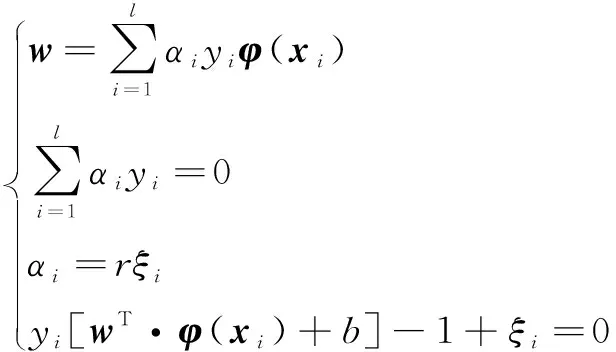
(6)

對于=1,2，…，，通過式(6)消去和，式(7)為經過解算推導出的LSSVM最優超平面公式，使用該式可訓練磨加工時輸入的尺寸數據。

(7)

其中核函數(,)即為某一空間內積()·()，因高斯核函數具有較少的核參數，模型的復雜程度較小，故核函數選用高斯核函數，公式如式(8)所示，其中為核參數。

(,)=exp[-(-)(2)]

(8)

在高斯核函數中，太小會導致過擬合，過大會影響判別函數的分布。核參數與懲罰參數共同決定了分類超平面的位置和形狀，它們取值過大或者過小都會影響LSSVM預測模型的泛化程度。故采用PSO對LSSVM的核參數和懲罰參數進行優化，提高LSSVM算法的線性回歸擬合和統計預測能力。設置粒子群數量，初始化粒子群參數、、、和循環次數，初始化核參數和懲罰參數。根據各個粒子位置坐標(，)，構建其對應的LSSVM預測模型，并對磨加工補調值進行預測。根據各LSSVM模型的預測結果，計算各LSSVM模型的預測誤差，并將它作為粒子個體適應度值。保存適應度值最優的粒子個體位置坐標(，)，更新各粒子個體的位置坐標(，)，根據更新后的(，)重新構建LSSVM預測模型，并對磨加工補調值進行預測。根據LSSVM模型的預測結果，重新計算各個LSSVM模型的預測誤差，確定適應度值最優的粒子個體位置坐標(，)。判斷是否滿足結束條件，若不滿足則循環執行上述操作，若滿足則根據適應度值最優的粒子個體位置坐標(，)，構建LSSVM預測模型并對磨加工補調值進行預測，完成磨加工補調值預測目標。PSO優化LSSVM模型流程如圖4所示。

圖4 PSO優化LSSVM模型流程

1.3 補調值在線預測與補償實現流程

利用模糊物元理論優化磨削工藝參數，將尋得的最優工藝參數組合輸入LSSVM補調值預測模型，采用PSO對預測模型中高斯核函數的核參數和懲罰參數進行優化。具體的磨削補調值在線預測與補償步驟如下：

(1)原始數據預處理，構建樣本數據，包括數據的粗大誤差剔除、數據的均值化、歸一化。

(2)利用模糊物元理論得出最優工藝參數組合。

(3)構建LSSVM補調值預測模型。預測模型訓練樣本集合為(,)(=1,2,…,)，為輸入值，是一個由組參數構成的維向量，即模糊物元理論得出的最優工藝參數組合；為相應的補調值。

(4)對模型作訓練學習，同時用PSO參數優化方法對預測模型參數尋優，選取最優參數。

圖5 補調值預測與補償實現流程

2 基于模糊物元分析的PSO-LSSVM磨加工補調值在線預測與補償實驗

2.1 磨加工主動量儀在線測量加工進程分析

在磨削加工過程中，當預測尺寸超出誤差允許范圍邊界時，向數控控制系統發出補調指令。控制系統接收指令后，通過更改工藝參數對誤差進行補調。砂輪進給機構和驅動裝置根據指令調整，實現工件尺寸閉環控制。利用在線測量進行磨削加工時，需要根據工藝規程設置特征點。加工進程被特征點劃分為5個階段：快速進給階段()-粗磨加工階段(-)-半精磨加工階段(-)-精磨加工階段(-)-光磨階段(-)，如圖6所示。

圖6 加工進程

測量裝置在快速進給結束時刻啟動，此時機床執行粗磨加工。當控制單元檢測到工件尺寸達到各階段尺寸要求時，數控系統自動調整工藝參數進入下一磨削階段，直至工件滿足設計要求(切斷點)，砂輪執行回程運動直至下一循環開始。由于精磨和光磨階段對加工質量影響明顯，故選擇精磨和光磨階段尺寸數據進行實驗。

2.2 實驗驗證與分析

為驗證基于模糊物元分析的PSO-LSSVM磨加工補調值在線預測與補償方法的有效性和準確性，設計并進行了在線測量磨削加工實驗。實驗裝置選擇高精度外圓磨床MGB1320E，磨削工件材質為45鋼，采用外圓徑向切入方式進行小批量磨削實驗，如圖7所示。

圖7 實驗裝置

由模糊物元分析可得最佳工藝參數組合如表1所示，采用該組工藝參數對工件進行加工。共進行35組實驗，每組加工20個工件，加工后工件尺寸采用氣動量儀測量，測量時每個工件選擇5個測量點，去掉極大值和極小值，取剩余3個值的平均值為尺寸實測值。通過求取實測值與公稱值之間差值得到補調值的實測值，可有效地去除測量偶然因素的影響。對采樣值誤差作均值處理，對每組實驗數據求均值，得每組的尺寸平均實測值、平均補調值，使得建模數據盡可能地擬合真實磨削數據。

表1 最優工藝參數組合

記錄每次磨削過程中各階段的尺寸數據用于預測模型訓練，并將訓練完成的模型應用于在線測量加工，驗證以預測值進行補調的磨削加工結果。程序均采用MATLAB編制。進行補調值預測時，采用PSO對LSSVM補調值預測模型參數尋優，得最優參數=0.615 5、=24.251 4。圖8所示為采用試樣內35組數據訓練所建立模型的參數和優化結果示意。圖中橫軸與縱軸分別表示和取以2為底的對數后的值，豎軸表示對應的預測精度，文中選用適應度函數值即均方根誤差作為評判準則。

圖8 PSO模型參數優化結果示意

表2為外圓磨削試驗補調值的實測值與預測值。補調值預測模型預測精度與穩定性的優劣采用平均絕對誤差(Mean Absolute Error,MAE)與均方根誤差(Root Mean Squared Error,RMSE)來評判，計算公式如下：

表2 工件外徑尺寸補調值實測數據及預測值

模型的與值越小，表示模型預測精度與穩定性越高。通過計算可得:預測模型獲得的補償值與實際應補償值的平均絕對誤差為=0.052 57 μm，均方根誤差=0.065 33 μm。圖9所示為補調值預測值與實測值對比曲線。

圖9 樣本內預測補調值與實測補調值對比

只采用樣本內數據驗證模型的精度時，會出現忽略過學習、泛化性弱、推廣能力不強的問題，難以確保模型的普適性。用所得補調值預測模型對試樣以外的批量工件進行外圓磨削加工實驗，分析模型對此補調值的預測精度，通過判斷預測精度能否達到主動測量控制儀的要求，來判斷模型的普適性。樣本外磨削試驗進行了8組，參數尋優得最優參數=6.498 0、=3.249 0，如圖10所示為采用樣本外8組數據訓練所建立模型的參數和優化結果示意，表3所示為磨削補調值實測值與預測值。

圖10 PSO模型參數優化結果示意

表3 磨削補調值實測值與預測值

預測結果表明：預測模型對試樣外的工件磨削補調值進行預測時，模型訓練樣本平均絕對誤差=0.096 25 μm，均方根誤差=0.134 12 μm。圖11所示為訓練樣本外補調值預測值與實測值對比。

圖11 樣本外預測值與實測值對比

將補調值預測模型應用于外圓磨削誤差反饋補償系統中，將模型預測所得補調值反饋到主動測量控制儀，在線控制磨削補調值的設置，加工一批工件尺寸為100 mm的柱狀工件，光磨余量定為7 μm，溫度為20 ℃，工件轉速為105 r/min，砂輪轉速為38 m/s。分析在誤差補償反饋控制情況下加工工件的精度。圖12所示為批量工件的尺寸分布。由統計結果可知：增加補調加工之后相對誤差的平均值和方差均有明顯提高，表明利用該預測模型進行在線預測和補調加工可有效提高加工精度。同時相對誤差的分布接近正態分布，表明該方法具有良好的重復性和較高的應用價值。

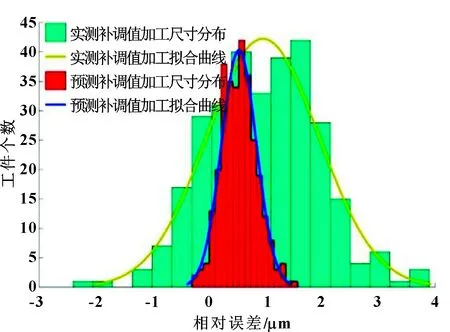
圖12 批量工件加工誤差分布

3 結論

針對現有磨削加工主動測量過程需要人工手動補調導致隨意性大、實時性差等問題，通過對磨削過程的分析和預報理論研究，提出了基于模糊物元分析的PSO-LSSVM補調值在線預測與補償模型，通過試驗驗證得到預測模型對試樣內以及試樣外的工件補調值預測精度高，符合補調值預測的精度要求。將模型應用于磨削加工時，對補調值作預測并及時反饋給磨床控制系統，實現自動調節工藝參數設置。研究成果有效地提高了產品加工精度的一致性和加工效率，對提升磨削加工智能化水平具有積極意義。