基于OPENSEEs的螺栓連接預制裝配剪力墻簡化建模方法

趙劍 ，姜紹飛，連晟航，李翔

(1.福州大學土木工程學院, 福建 福州 350108; 2.福建工程學院土木工程學院, 福建 福州 350118)

0 引言

預制裝配鋼筋混凝土結構按照連接方式可分為干連接和濕連接兩種[1].濕連接指通過套筒連接或者漿錨連接的方式將預制剪力墻的豎向鋼筋與下層結構主體中的豎向鋼筋等強連接，從而達到總體結構“等同現澆”的效果.干連接是指通過螺栓連接、 焊接連接、 預應力筋連接等進行快速裝配施工.其中，螺栓連接裝配剪力墻是一種很有應用前景的干連接裝配剪力墻結構.很多學者對不同形式的螺栓連接裝配剪力墻展開擬靜力試驗[2-7]，結果表明螺栓連接傳力可靠，通過合理設計，該類預制剪力墻擁有良好的抗震性能.王維[8]通過振動臺試驗，對比分析了采用螺栓連接裝配剪力墻結構體系與相應的現澆結構的動力抗震性能差異.當前螺栓連接裝配鋼筋混凝土剪力墻結構的研究主要集中在試驗研究，這雖然可以真實地反映螺栓連接預制裝配剪力墻的力學性能和受力情況，但受到時間、 經費與試驗條件的限制，無法對各個影響參數進行全面測試.而數值仿真已被證實能較好地模擬試件的內力分布及變形[9-12]，可以對試驗的其他影響參數進行補充模擬，省時省力、 節約經費，已成為重要的科研工具.因此，發展螺栓連接預制裝配剪力墻力學性能的有限元仿真技術，對全面研究拼接區及整體結構的受理機理具有重要的意義.

目前仿真建模主要分為精細化建模與簡化建模.精細化建模由于建模精細、 物理信息明確，近年被用于螺栓連接裝配剪力墻的建模中[6, 13-14]，但其計算代價高，且計算結果文件巨大從而影響其在復雜結構的非線性分析與推廣.因此，有必要在保證計算準確率和正確反映結構特性的基礎上，進行基于桿系和殼單元的簡化建模研究.現澆剪力墻典型簡化建模方法主要有Vecchio等[15]的壓力場理論、 Kaba等[16]的基于柔度法的纖維模型、 Vulcano等[17]的多垂直桿模型, 以及 Lu等[18]的分層殼單元等.其中，Lu等[18]的分層殼單元可以針對不同剪跨比的剪力墻，結構建模比較簡單，得到較普遍的應用.但是，對于螺栓連接裝配剪力墻結構，其連接區結構形式較為復雜，如何對螺栓連接進行簡化建模、 先后澆筑混凝土界面簡化處理等現有這些建模方法均不適用.基于此，本研究采用OPENSEEs軟件，對兩種不同類型的干連接裝配RC剪力墻結構分別提出對應的基于桿系單元及殼單元的簡化建模方法.通過6個一字型干連接裝配剪力墻的擬靜力仿真試驗，對滯回曲線、 骨架線、 承載力特征值、 鋼筋應變、 連接鋼框滑移等進行仿真與試驗結果比較，來驗證建模方法的可行性和有效性.

1 螺栓連接裝配剪力墻試驗簡介

開展1個現澆及6個螺栓連接裝配剪力墻的低周往復加載試驗[14].試驗參數包括剪跨比、 裝配方式，如表1所示，其中剪跨比通過墻身高度來調節，墻身寬度、 厚度及配筋方案保持不變.裝配方式分為現澆、 半裝配及全裝配.墻身豎向鋼筋與預埋的鋼框通過雙側角焊縫連接，焊縫強度滿足強于母材鋼筋的極限抗拉強度要求.螺栓連接采用8.8級M18螺栓，栓孔直徑20 mm，混凝土強度設計等級為C40，除箍筋為HPB300外，其他鋼筋均采用HRB400，鋼材材性如表2所示.試件典型配筋如圖1所示，連接鋼框尺寸如圖2所示，鋼框與螺栓接觸面為未經處理的干凈軋制表面.水平加載前先施加318 kN的軸壓力(軸壓比0.2)，然后按1.0、 2.0、 3.0、 3.5、 4.0、 4.5、 5.0 mm施加墻頂位移，每級往復循環一次.確定屈服位移為5.0 mm后，按每級增加5.0 mm進行加載，每級循環3次.

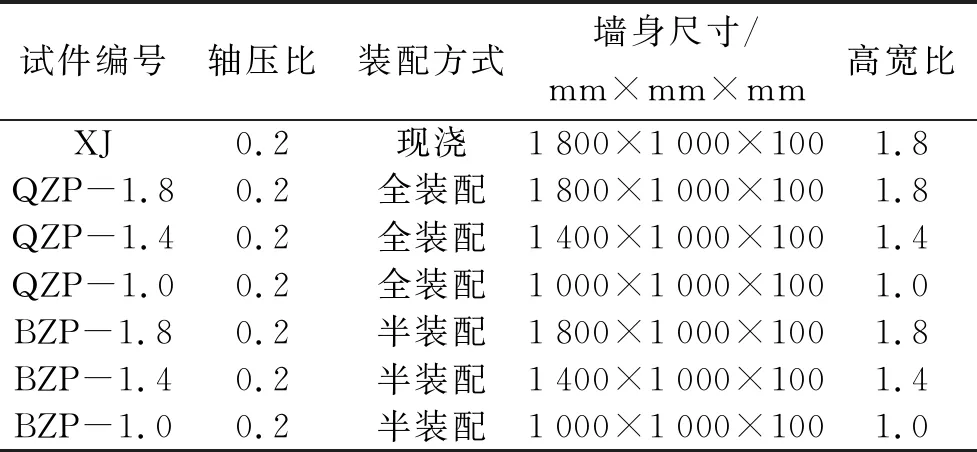
表1 試件參數

表2 鋼材材性

2 螺栓連接裝配式剪力墻數值建模方法

2.1 剪力墻的單元模型及本構選取

墻體采用Lu等[18]提出的分層殼單元來模擬，混凝土本構采用基于損傷力學和彌散裂縫模型的多維混凝土材料本構，墻身鋼筋采用基于Steel02單元的多維鋼筋材料模型.為方便觀測和記錄邊緣豎向鋼筋的應力以判定剪力墻構件屈服情況，將邊緣約束構件的豎向鋼筋單獨用桁架單元來模擬.模擬剪跨比為1.8的現澆剪力墻，墻頂力—位移滯回曲線與試驗曲線對比如圖3所示.由圖3可知，模型的模擬效果較好，構件初始剛度、 峰值承載力、 極限承載力與試驗值基本一致.其中，負向承載力峰值試驗值為-228.3 kN，仿真計算結果為-222.8 kN，相差2.4%，正向承載力峰值試驗值為254.4 kN，仿真計算結果為223.5 kN，相差12.1%.仿真得到的峰值荷載對應的位移正向20 mm，負向-20 mm，試驗值分別為25和-15 mm.正向峰值承載力存在較明顯差異的原因在于試驗構件加工及制作誤差.若對正負向峰值承載力取均值作為構件峰值承載力，則二者相差7.5%.取正負向峰值荷載對應位移的平均值來對比，二者均為20 mm，試驗和仿真結果吻合良好.

2.2 螺栓連接的單元及本構選取

螺栓連接本構參考王萌等[19]提出的循環荷載作用下的高強螺栓連接滯回模型.這種螺栓滯回本構考慮到螺栓在往復加載條件下的滑移現象，能在較小的計算代價下較為準確和高效地模擬螺栓抗剪行為.采用單軸材料本構hysteretic material來實現單螺栓連接滯回模型的模擬.由于構件均是采用雙排布螺栓連接，兩排螺栓間距較小，采用簡化建模方案，如圖4所示.即螺栓連接處設置于兩排螺栓中間位置，改成單排布螺栓，螺栓的力學性能設置上橫坐標的滑移值不變，豎坐標螺栓承載力數值翻倍.螺栓模擬單元選取零長單元CoupledZeroLength.該單元是一種兩相同位置點間的零長單元，可以提供圓周徑向的界面相互作用力，相比于通過ZeroLength單元提供兩個垂直方向的力，更適合用來模擬螺栓連接.建立單一螺栓連接模型，對周期往復加載情況下的螺栓連接性能進行測試，單元滯回材性選取hysteretic material滯回本構，特征點力位移參數經計算選取，正方向首點橫縱坐標分別為135.0 kN和0.06 mm，第二點橫縱坐標為135.0 kN和1.85 mm，峰值點橫縱坐標為223.8 kN和3.2 mm，負方向和正負向取值對稱.其他滯回及損傷計算參數$pinchx、 $pinchy、 $damage1和$damage2參數取值對照王萌等[19]提出的高強螺栓連接滯回模型, 以及OPENSEEs幫助文件中針對hysteretic material詞條中展開的滯回相關參數影響圖例說明, 經過單一彈簧建模調試，分別取0、 1.0、 0和-2.0.

測試結果如圖5所示.此處應該注意的是，由于hysteretic material中的特征點是不包含剪切破壞后彈簧失效的觸發機制，因此在計算完成后應對各個螺栓對應的零長單元的最大內力進行核驗，如果超過抗剪承載力，則應在計算分析步中對應計算節點處增加一個新的計算節點，使該處的彈簧退出工作，如此往復直到計算結束.

2.3 半裝配剪力墻豎向齒槽連接的模擬

在采用桿系和殼單元進行宏觀模擬時，對先后澆筑的豎向混凝土接縫處的齒槽構造連接作簡化處理，即在齒槽位置處設置一條寬度20 mm的條帶，如圖6所示.作為先后澆筑混凝土的交界面，仍然采用分層殼單元模擬此交界面.不同的地方在于，和預制墻身相比，混凝土的材性中極限抗拉強度設置成一個較小值，即連接區混凝土抗壓不抗拉.以BZP-1.8試件的建模方案為例，經最終網格劃分和簡化建模建立模型如圖6所示.

2.4 加載控制及計算求解單元設置

和試驗加載一樣，加載分為軸力施加和墻頂位移施加兩步，均選取適用于靜力分析的Load Control積分選取方案.約束方式選取constraints Penalty，編號排位方式選取RCM numberer，自由度存取方式選擇BandGeneral，收斂準則選取NormDispIncr，算法方案選擇KrylovNewton，分析類型選取靜力加載analysis Static.

3 數值建模驗證與應用

3.1 滯回曲線及骨架線對比

基于上述建模方法，對6片不同剪跨比的全裝配和半裝配鋼筋混凝土剪力墻進行擬靜力仿真分析，得到的墻頂力—位移關系滯回曲線和試驗對比如圖7所示，骨架線對比如圖8所示.

從圖7～8中可看出： 1) 有限元模型的滯回曲線與試驗曲線均呈現較為飽滿的梭形，反映出鋼筋混凝土結構滯回性能的“捏縮”特性.2) 有限元模型的初期剛度略大于試驗的剛度，其原因是： 試件加載裝置中，如加載地梁底面與地面之間存在微小的滑移，加載梁與抱頭抱板間存在的初始間隙等均會使得試驗所測得的剛度降低.對于剪跨比較小的構件，如BZP-1.0與QZP-1.0，同級別加載下底部承受水平剪力更大，因此會更早地出現加載梁與地面之間的滑移，導致測量到的初期試驗剛度偏低.3) 模擬曲線的強度退化與剛度退化特性也與試驗情況較為吻合.

3.2 鋼筋應力應變對比

本次試驗的6片剪力墻構件均是以邊緣豎向鋼筋斷裂為破壞標志，因此，該處鋼筋的各個階段的應力應變表現可以從另一個側面驗證本文仿真方法的有效性.以QZP-1.8和BZP-1.8為例，其邊緣豎向鋼筋的底部應力與加載位移關系曲線的試驗與數值仿真結果對比如圖9所示.可以看到，加載初期由于前文所述的試件加載裝置間隙帶來的滑移因素影響，模擬的鋼筋前期應變增長速率要快于試驗值，所以鋼筋更早地達到了屈服應變，導致總體上看模擬的曲線要比試驗曲線“飽滿”.隨著加載級別的增大，二者差異逐漸減小，到加載級別達到15 mm時，從圖9中的正向應變峰值對比來看，其與試驗值的差異已經很小，在10%以內.

本次擬靜力試驗的屈服承載力是以約束邊緣構件的外側鋼筋屈服進行定義，因此，該處鋼筋的應力應變關系曲線對于確定構件的屈服承載力有重大意義.結合仿真的剪力墻約束邊緣構件的底部豎向鋼筋的應變監測，給出6個構件的典型特征承載力對比，列于表3.Fy為屈服承載力，Fmax為峰值承載力.可以看到模擬的6條滯回曲線其屈服承載力及抗側承載力峰值均與實驗值較為吻合，除了BZP-1.8構件的屈服承載力可能由于試件制作和材性離散，以及鋼筋應變片數據采集質量帶來的差異偏差值在13%外，其余的數據偏差在10%以內，可以較好地反映結構抗震承載力特征值.特征承載力對應位移對比分析如表3，Sy為屈服承載力對應位移，Smax為峰值承載力對應位移.可以看到特征承載力對應的位移仿真值和試驗值存在一定的差異.原因在于試件加載裝置初始間隙等原因使得試驗所測得的初期剛度相比仿真結果低，從而導致試驗屈服位移比仿真值要大2.5 mm左右.受此影響，加上試件下降段延性模擬的偏差，仿真得到的峰值承載力對應位移相比試驗值偏差在一級加載級差，即5 mm左右.

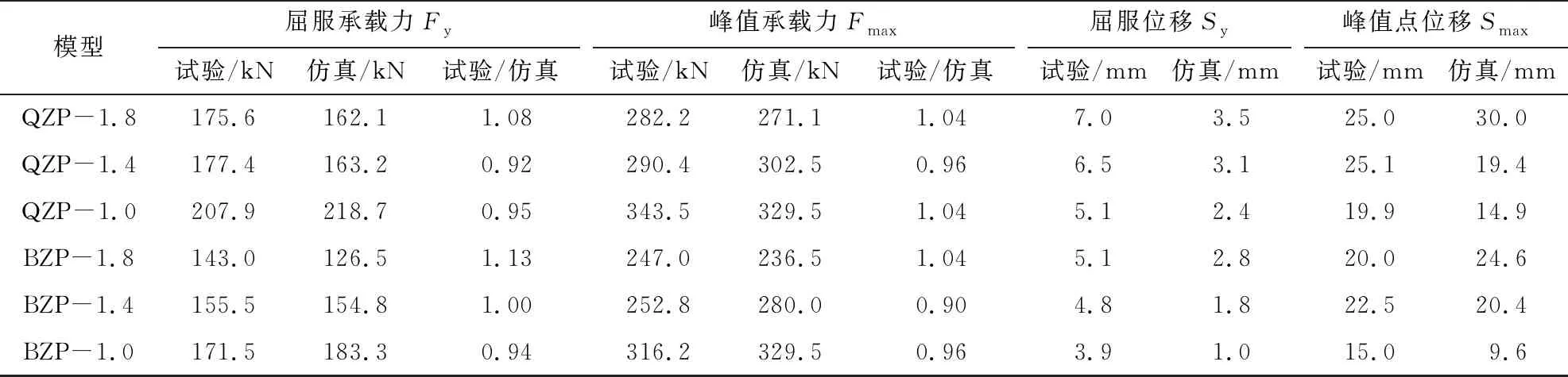
表3 特征承載力及對應位移對比分析

3.3 連接件滑移對比

采用螺栓連接的裝配剪力墻區別于灌漿套筒等“濕”連接，以及傳統現澆剪力墻的最顯著力學特性在于后期彈塑性階段上下連接鋼框間的滑移，滑移的模擬是否準確也可為仿真分析是否有效提供驗證.由于半裝配剪力墻結構兩側約束邊緣構件采用現澆，因此裝配剪力墻上下鋼框水平向的滑移僅在全裝配結構上檢測到，以QZP-1.8與QZP-1.4構件為例，仿真與試驗結果對比如圖10所示.其中，對于QZP-1.8試件，其鋼框水平滑移試驗測得的正向最大值為0.28 mm，仿真得到的為0.28 mm.負向滑移試驗測得最大值為-0.58 mm，仿真結果為-0.79 mm.

對于上下鋼框間的豎向滑移的對比以QZP-1.4與BZP1.4構件為例，如圖11所示.

其中BZP-1.4模型的豎向滑移的正向最大值為0.37 mm，仿真結果為0.81 mm，負向試驗測得豎向滑移最大值為-2.2 mm，仿真結果為-2.0 mm.可以看到，總體上，仿真得到的豎向和水平向滑移值與試驗所測到的滑移值雖略有差異，但總體變化規律相似.造成差異的原因主要是考慮到本身滑移值較小，試驗監測過程影響數據精度因素眾多，例如位移計安裝不水平、 本身試驗裝置間隙等因素影響.本研究的簡化建模辦法可較好地模擬螺栓連接裝配剪力墻的連接鋼框間的滑移，可為后續開展該類裝配剪力墻滑移的進一步研究提供參考.

4 結語

1) 本文提出的建模方法可較好地預測螺栓連接裝配剪力墻的屈服承載力、 峰值承載力等抗震滯回性能指標，也能較好地反映出該類結構的擬靜力試驗滯回曲線的“捏縮”特點，以及強度和剛度退化規律.

2) 采用螺栓連接干式裝配剪力墻的顯著特點在于彈塑性后期階段上下連接鋼框間的滑移，采用本文提出的建模方法可以對滑移及關鍵部位的鋼筋應力應變發展進行比較有效的預測.

3) 所給出的建模方法具有較高的計算效率和較好的計算精度，可進一步應用于采用螺栓連接裝配剪力墻結構高層、 超高層結構的彈塑性分析.