重載交通作用下橋梁結構承載能力研究

蔡岷山

（青海省育才公路勘察設計有限公司,青海 西寧 810000）

超限、超載貨車的增多致使橋梁更易產生嚴重病害,給橋梁帶來嚴重威脅：使得橋梁承載能力下降,影響其使用性能,縮短橋梁內部結構壽命[1]。針對這一問題,本研究建立有限元模型,綜合考慮貨運車輛超限超載情況,真實還原超限超載貨車過橋場景,對橋梁關鍵截面的受力情況和橋梁的承載能力進行計算并分析。較之傳統的以標準車型標準荷載為依據的模擬方法更加全面、科學、合理。

1 橋梁有限元模型的建立及適用性驗證

根據高速公路實際通車情況,代表橋型取設寬度為24.5 m 的整體式路基,上下行分幅、長度為20 m、設計荷載等級為公路-I 級的簡支T 梁橋。以空間梁格理論為基礎,利用ANSYS14.0 建立橋梁有限元模型,根據梁板實際受力情況,取Beam4 作為主梁單元類型。一般情況下通常忽略橋面鋪裝層對主梁慣性矩的作用,但建立模型時,考慮到橋梁整體截面高度相對較小,橋面鋪裝的作用不能忽略不計。再綜合考慮實際情況,因此此處忽略瀝青磨耗層的影響,將10 cm 厚混凝土鋪裝層和橋梁頂板視為一體,構建模型。簡支T 梁的現澆接縫與主梁的翼緣板之間連接剛度較強,建模時將二者視為一個整體考慮。采用Solid65單元對選用的標準橋梁實體結構進行精細化模擬,以實體有限元模型為基礎,分析驗證梁格法有限元模型的合理性和適用性。

在兩種模型的不同位置分別施加同樣的荷載,分析對比兩種模型中各個板（梁）的位移情況,以其相似程度判定梁格法模型的有效性和適用性[2]。

工況1：考慮中載作用,即在3 號梁（3#）跨中處施加大小為1 000 kN 的集中力。

工況2：考慮偏載作用,在1 號梁（1#）跨中處施加大小為1 000 kN 的集中力。

兩種模型中各片梁的位移對比結果見圖1。

圖1 各加載工況下兩種模型位移對比

圖1 的位移曲線直觀反應出兩種模型的位移變化具有較高程度的吻合性。對其誤差進行深入分析可知,兩種工況下的位移誤差都不超過5%。因此用梁格法建立的橋梁有限元模型具有較好的適用性,可以用于接下來的分析。

2 重載交通作用下橋梁荷載效應分析

在分析系統中對梁格法有限元模型進行分析,計算出不同荷載情況下橋梁關鍵截面的內力效應,詳見圖2。

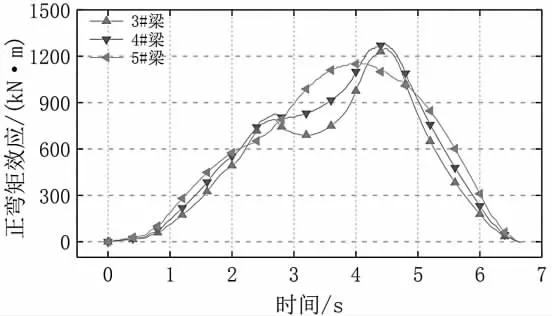
圖2 行車道各片板正彎矩響應時程曲線

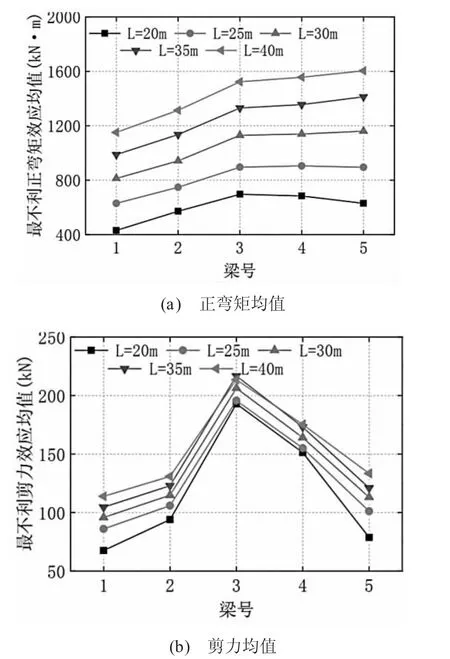
圖3 簡支T 梁橋空間結構響應特征值隨跨徑變化

3 橋梁結構承載能力響應特征分析

橋梁結構以承彎為主,對橋梁結構的各片板（梁）在重車荷載作用下的效應特征分析時,取正彎矩效應及剪力效應進行分析比較適宜[4]。重車荷載作用下的標準橋型的各片板（梁）的最不利正彎矩響應和最不利剪應力響應的極值、均值及標準差分別見表1、表2。

表1 正彎矩效應響應特征分析

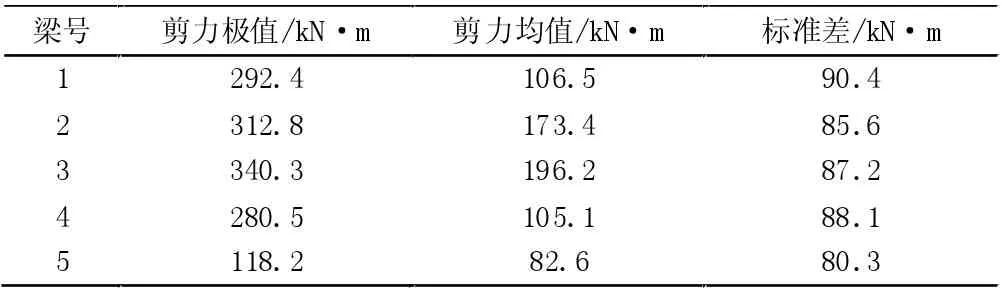
表2 剪力效應響應特征分析

4 重載交通作用下橋梁結構抗裂性能分析

基于超靜定結構的特點,對簡支T 梁橋進行荷載模擬時應考慮恒載效應及汽車荷載效應。與簡支T梁橋不同,對連續箱梁橋這一超靜定結構進行荷載效應短期組合時,鋼束次內力、支座的沉降、收縮徐變等產生的正彎矩效應都應綜合考慮。可用如下方程式表征[5]：

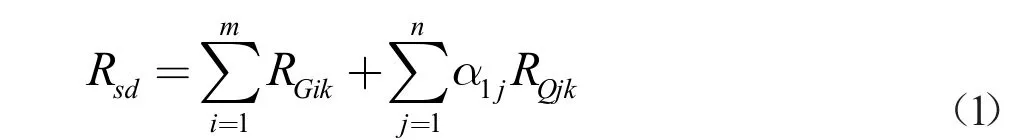
式中：α1j為第j 個可變作用效應的頻遇值系數,對橋梁板而言,常見的可變作用效應有汽車荷載、溫差等。其中,對于不計沖擊力的汽車荷載,α1=0.7；對于溫度梯度,α1=0.8；對于其他作用,=1.0。

對混凝土構件的抗裂性能進行分析時,可以從其關鍵截面的底部邊緣處混凝土的應力狀態著手。對簡支T 梁橋這一全預應力混凝土構件進行抗裂性能分析時,在短期效應組合下,其正截面底部邊緣混凝土的受力狀態應處于式（2）范圍內：

式中：σst為在短期荷載組合對截面作用下產生的應力; σpc為預應力引起的截面壓應力。對超限超載車輛通過橋梁時的應力狀態進行模擬計算和統計分析。重車荷載作用下雖然平均處于受壓狀態,但是在部分重車荷載作用下,橋梁結構關鍵截面底緣混凝土出現了受拉情況,而這是規范所不允許的,也是我們在實際中需要避免的。

5 重載交通作用下橋梁抗彎承載能力分析

引入 η作為衡量橋梁承彎能力的指標。考慮橋梁在一般服役狀態中及重載交通作用下的實際受力情況,分析對比關鍵截面的荷載效應組合與正彎矩效應的抗力值大小,以此為基礎可以得到經過量化評估后的橋梁承載能力安全性評價,對于任意一輛重車通過橋梁時的工況i,其結構安全性評價指標 ηi可以用式（2）表示：

其中,RGik為恒載效應,λGi=1.2；RQ1k為汽車荷載效應；為除汽車荷載效應之外的其他可變荷載效應,λQj=1.4；υc根據RQjk（j≥2）的數量予以確定,P 為橋梁結構的自身抗力。

由式（3）可知,式中的唯一變量為每一輛特重車輛通過橋梁時對橋梁結構產生的最大彎矩效應。結構的恒載效應、溫差效應等視為常量處理。

對不同跨徑的橋梁在重車荷載作用下的彎矩承載能力 η進行分析,η 值的極值和均值都在一定水平上下浮動,η與橋梁的跨徑大小無直接關系。對于簡支T 梁這一橋梁結構,η 值的均值在0.58 左右,極值低于1.0,說明對于簡支T 梁,重車荷載的作用在橋梁結構的極限承載能力之內。

6 車輛限載關鍵問題處理

以可靠度理論為基礎對橋梁車輛限載情況進行分析時,構造出正確的極限狀態方程是必須首先完成且極其重要的一項工作,而主要隨機變量的分布參數及分布類型的確定對方程構建的正確與否至關重要。另一個相當重要的工作的是根據選定的目標可靠指標反向推算出對應的重車荷載分布,并由得出的荷載分布來計算正彎矩效應的范圍,確定閾值。

在具體分析時,選定結構自身抗力、恒載作用效應、重車荷載效應為主要隨機變量,構建極限狀態方程如式（4）：

式中:R 為結構抗力；G 為恒載效應；Q 為重車荷載作用；m 為其他荷載效應。

本研究取目標可知目標可靠指標所對應正彎矩效應分布的均值作為正彎矩效應閾值。在研究時,選取0.2～0.7,變化梯度為0.1 的變異系數為控制變量,分別計算其對應的正彎矩效應閾值,結果見圖4。

圖4 變異系數對正彎矩效應閥值的影響分析

由圖4 可知,正彎矩效應閾值隨著變異系數的增大而下降,且降幅明顯。這也意味著變異系數的選取對計算結果影響較大,在確定變異系數時須進行綜合全面而又科學合理的分析。

7 結論

綜上所述,本研究先以空間梁格為依托建立橋梁有限元模型,通過與橋梁實體有限元模型進行對比分析,驗證其可靠性及適用性。在梁格有限元模型的基礎上,利用matlab 對重車荷載作用下橋梁各片板（梁）的空間響應特征等數據進行計算分析,得出一系列關于重載交通環境下橋梁的內力、抗裂性能、承載能力等結論。主要如下：

（1） 橋型不變的情況下,重車荷載響應的水平隨橋梁跨徑的增大而不斷提高,但響應特征的變化趨勢不受橋梁跨徑影響。

（2） 對于簡支T 梁橋的各片板（梁）,其極值響應呈現明顯的單峰特性,并且其正彎矩極值響應特征與剪力極值響應特征有一定差別。

（3） 板（梁）的平均響應水平受車輛行駛規律影響較大。對于簡支T 梁橋而言,3 號梁的平均響應水平最高。