輸氣管道受占壓荷載的有限元安全分析
慕 園,宋梅梅,李崇健,卜武軍,李昆昆
(1.四川國銳工程設計有限公司西安分公司,陜西 西安 710018;2.西安石油大學機械工程學院,陜西 西安 710065)
引言
道路等線性設施與輸氣管道交匯頻繁,其改擴建會對交匯處管道形成占壓,威脅管道的安全[1]。輸氣管道規范的公式法更適于驗算新建管道的徑向穩定,眾多管道受占壓案例[2]表明,在役管道受占壓宜進行專項分析。因ABAQUS 軟件在處理非線性問題時優勢明顯[3],故本研究采用ABAQUS 構建管土相互作用[4],考慮地應力平衡,對受占壓管道進行安全分析。
1 有限元建模
1.1 工程案例
某輸氣管道規格為D508×8 mm L415 鋼管,在河堤內側的敷設埋深約2 m。河堤在與橋梁交匯處發生決口,水務局采取在橋梁兩側拋填土石的方式攔截洪水。橋梁一側填方范圍為12 m×8 m,另一側為18 m×10 m,平均厚度為4 m。管道與河堤、路基段的相互位置見圖1。因堆載過大會引起管道變形或位移[5],故亟需對受占壓管段進行評估。
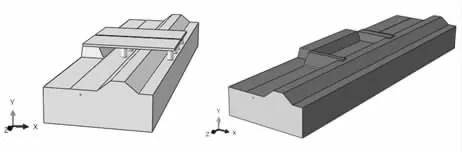
圖1 堆載前后管道與河堤、路基相互位置關系
1.2 建模參數
1.2.1 地層參數
占壓段地層以粉質黏土、粉土為主,力學參數見表1。土層采用Mohr-Coulomb 本構。
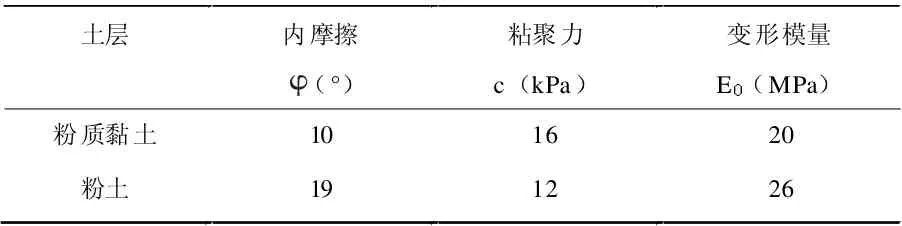
表1 各土層力學參數
1.2.2 管道參數
管道的力學參數見表2。

表2 管道力學參數
1.2.3 填方參數
堆填土石的力學參數參考《地質工程手冊》[6]取值,見表3。
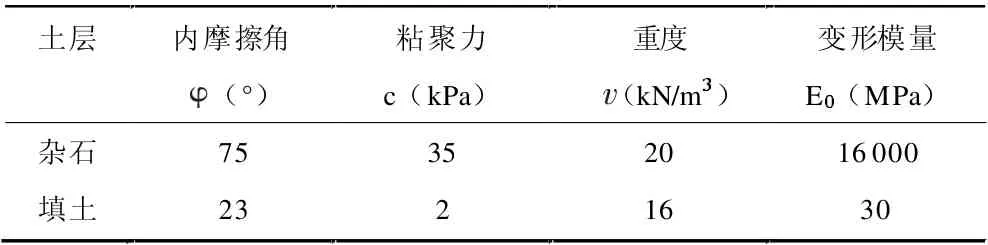
表3 填方力學參數
1.3 網格模型
路基、河堤、場區土層均采用C3D8 體單元,管土接觸處網格進行細分[7],管道用S4R 殼單元,雜填土用C3D4 體單元。網格模型及接觸處細分網格見圖2。
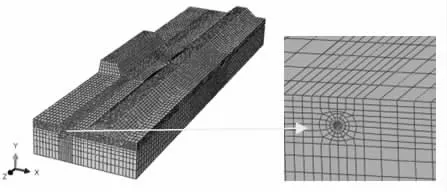
圖2 網格模型及管土接觸處細分網格
1.4 邊界條件與接觸定義
場區土體四周約束X、Y 方向自由度,土體底部約束Y 自由度。填土、路基、河堤及管道間的接觸均定義為摩擦接觸。
1.5 分析步驟
1.5.1 地應力平衡
先移除管土相互作用,施加重力荷載,輸出土體節點應力。然后在Input 文件中添加土體節點應力,模擬地應力平衡。
1.5.2 激活接觸
激活管土接觸,模擬填方前管道受力情況。
1.5.3 施加填方荷載
對于f2的分析如下,每個電子都受到垂直于導線的分力f2,而導體棒受到向左的力F總則是這些分力f2的合力。我們可以先假設該導體棒的長度為L,其橫截面積為S,在單位體積內的電荷數為n,且做定向運動的自由電子的電量為e。
在Input 文件中用關鍵字Model change 設置堆載過程。
2 有限元分析
2.1 填方前管道狀態
填方前管道位移見圖3。管道最大位移值約為2.3 mm,數值極小。管道應力幅值為136~140 MPa。管道位移和應力分布均符合實際情況。

圖3 填方前管道狀態
2.2 填方后管道狀態
填方后管線的應力和位移見圖4。管道最大位移值約54 mm,管道最大主應力為179 MPa,發生填方重量較大的位置。

圖4 堆方后管道狀態
3 計算結果分析
3.1 強度校核
(1) 按照輸氣管道規范,管道強度應滿足公式(1)。式中σ1、σ3表示最大、最小主應力,σe表示當量應力。
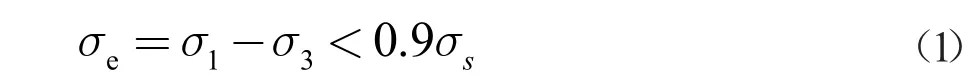
經核算σ1=179 MPa,σ3=32.4 MPa,σe小于0.9 σs,滿足規范要求。
(2) 根據第四強度理論,管道強度應滿足公式(2)。式中σ2、[σ]分別表示中主應力和許用應力,seff表示等效應力。
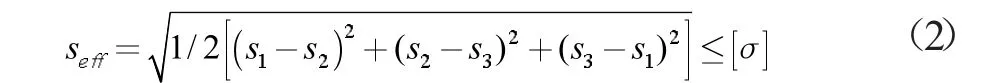
經核算seff=182.8 MPa,較許用應力小,滿足強度要求。
3.2 位移驗算
堆填前管道最大位移為2.3 mm,堆填后為54 mm,重載引起管道在不同部位的位移差值較大。根據彎曲變形理論,受堆載管道可按局部彈性地基梁模型[8]驗算撓度。撓度估算公式見式(3)~(5)。

式中:q 表示線荷載(kN/m),為36.576 kN/m。l 表示占壓段,取10 m。鋼管彈性模量E=2.1×105MPa。管道橫截面慣性矩I=3.928×10-4m4。參照王國體等人對彈性地基梁的研究[9],土層地基系數k 取10 000 kN/m3。經計算,管道最大撓度ω1=57 mm,管底土體豎向位移為ω2=-7.2 mm,管道最大撓度ωmax=49.8 mm。公式法估算值與有限元計算值較為一致。
3.3 抗外壓穩定驗算
輸氣管道規范按無內壓狀態校核抗外壓穩定性,管道徑向最大變形量△X需滿足式(6)、(7)。

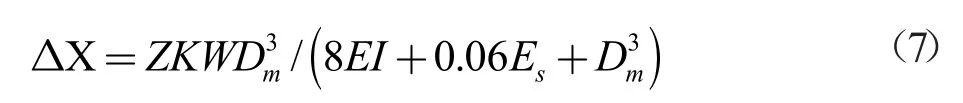
式中:Dm表示鋼管平均直徑(m);W 為作用在單位管長上的總豎向荷載(N/m),W=W1+W2,W1表示單位管長的豎向永久荷載,W2表示地面可變載荷傳到管道上的荷載;鋼管變形滯后系數Z 取1.5;鋼材彈性模量取2.1×1011N/m2;基床系數K 取0.108;土壤變形模量Es取1×106N/m2。經核算 ΔX為15 mm,能夠滿足抗外壓穩定要求。
4 結論
(1) 有限元法分析管道占壓安全的關鍵在于合理選用單元類型,正確處理管土接觸。
(2) 輸氣規范以應力是否超標校核管道安全,未限定撓度值,而數值法可形象揭示管道位移變化,對撓度進行驗算。但數值結果應用于結構分析前還應用公式法校驗。

