基于ANSYS的H型剛?cè)狁詈蠙C械臂動力學建模與動態(tài)特性機理研究

聞 志，沈金淼，孔 輝，張文輝,4,5，游張平

（1.浙江理工大學機械工程學院，浙江 杭州 310018；2.南京曉莊學院電子工程學院，江蘇 南京 211167；3.麗水學院工學院，浙江 麗水 323000；4.浙江省航空航天金屬導管塑性成形技術與裝備重點實驗室，浙江 麗水 323000；5.浙江省文創(chuàng)產(chǎn)品數(shù)字化設計與智能制造重點實驗室，浙江 麗水 323000）

自從20世紀60年代第一臺機器人誕生以來，機器人技術[1]在學術研究、工業(yè)生產(chǎn)等方面得到了飛速發(fā)展。機械臂作為一種特殊的機械結(jié)構(gòu)[2]，因其具有輕型化、高效性、獨立性等優(yōu)點[3]，并且能夠完成高精度、高要求、高危險等任務，被越來越多地應用在航空、醫(yī)療、軍事、工業(yè)生產(chǎn)等領域[4-6]。隨著科學技術的不斷發(fā)展，對機械臂的要求也越來越高，對機械臂而言，輕型化、高速度、高精度是現(xiàn)代設計的必然要求[7]，整個機械系統(tǒng)演變?yōu)閯傮w與柔性體相耦合的動力系統(tǒng)[8]。在高精確運動要求前提下，就必須考慮機械臂的彈性變形對運動精度的影響[9-10]。因此，筆者從柔性宏剛性微機械臂的優(yōu)化設計角度，對剛?cè)狁詈蠙C械臂的動態(tài)特性及內(nèi)在機理進行分析研究。

柔性操作臂是典型的剛?cè)狁詈戏蔷€性動力學系統(tǒng)，研究其動力學特性問題，需要建立系統(tǒng)的動力學模型。近年來，宏柔微剛機械臂被越來越多的學者所研究[11-12]。崔玲麗等[13]考慮機械臂的形狀參數(shù)及驅(qū)動器的參數(shù)，基于有限元分析法，構(gòu)建了非均勻截面梁系統(tǒng)的動力學模型；Kane等[14]基于模態(tài)綜合法對運動基柔性梁建立了較為準確的動力學方程，對系統(tǒng)的動力學特性進行了研究；王從慶等[15-17]又采用拉格朗日法推導了平面三連桿剛?cè)狁詈蠙C械臂的動力學模型，并通過實驗測試驗證了該模型的合理性；Yang等[18]學者基于假設模態(tài)法，利用傳感器測得的柔性操作臂線性位移以及關節(jié)轉(zhuǎn)角推導了柔性多連桿操作臂的動力學模型；Khairudin等[19]學者利用拉格朗日方程及假設模態(tài)法推導了雙連桿柔性操作臂的動力學模型。

考慮到柔性宏剛性微機械臂是一個多變量、非線性復雜的動力學系統(tǒng)，故要想全面了解其動力學動態(tài)特性，有必要對其固有頻率特性和內(nèi)在機理進行深入研究。首先，基于有限元法和拉格朗日方程完成對柔性多體系統(tǒng)動力學模型的構(gòu)建；其次，分別從截面參數(shù)、材質(zhì)組合、集中質(zhì)量等方面分析各因素對系統(tǒng)固有頻率特性的影響，研究各參量與剛?cè)釞C械臂固有頻率之間的關系，分析不同設計參量對宏微機械臂固有頻率特性的影響規(guī)律和作用機理。

1 柔性宏剛性微機械臂模型建立

機械臂的模型建立是其動態(tài)特性分析的重要內(nèi)容，是系統(tǒng)整體結(jié)構(gòu)設計和優(yōu)化的前提。精確的動力學模型也為控制系統(tǒng)描述及控制器設計提供有效的依據(jù)。動力學建模通常是基于混合坐標的建模方法，當系統(tǒng)做大規(guī)模運動時，自身結(jié)構(gòu)發(fā)生彈性變形，具有較強的剛?cè)狁詈闲浴９P者基于彈性動力學分析方法通過離散機械臂單元自由度，描述機械臂的彈性變形，為后續(xù)進一步研究柔性宏剛性微機械臂的動態(tài)特性奠定了基礎。

柔性宏剛性微機械臂的系統(tǒng)模型如圖1所示。當分析其彈性變形時，假設桿1、桿2分別為單個結(jié)構(gòu)單元體。

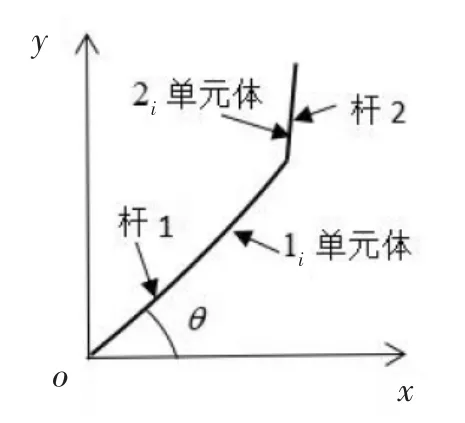
圖1 宏柔微剛機械臂系統(tǒng)模型

系統(tǒng)的運動微分方程一般表示為

式中：M表示質(zhì)量矩陣；C表示阻尼矩陣；K表示剛度矩陣；P表示廣義力矩陣；表示一個8維列陣；U表示彈性位移矩陣。與U滿足以下關系：

其中Bi表示一個8×9的坐標協(xié)調(diào)矩陣。

同理，有

將式（2）和式（3）代入式（1），并左乘得

式中：

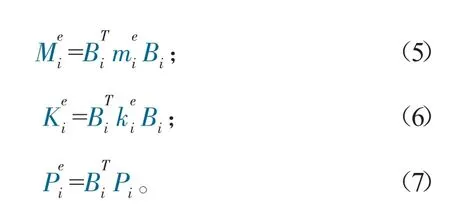
將所有單元運動方程相疊加即可得到柔性宏剛性微機械臂系統(tǒng)運動方程為

2 柔性宏剛性微機械臂固有頻率分析

2.1 頻率特性參量定義

由彈性動力學分析方法可知，系統(tǒng)的動力學方程式為

式中：M為質(zhì)量矩陣；K為剛度矩陣；P為廣義力矩陣；U為彈性位移列陣；為彈性加速度列陣。

固有頻率w可由式（9）的特征根求得，即

式中，I為單位矩陣。

由式（10，11）可知系統(tǒng)的固有頻率w與質(zhì)量矩陣和剛度矩陣有關。

由此可得每一個單元體固有頻率的表達式為

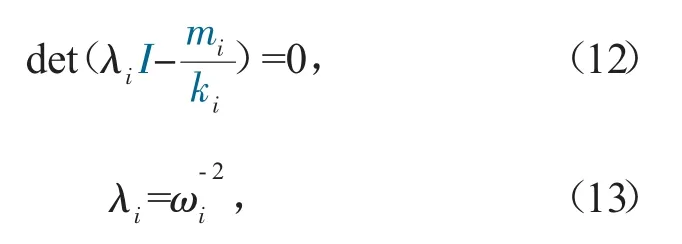
式中：mi為單個單元體質(zhì)量矩陣；ki為單個單元體剛度矩陣。其中，

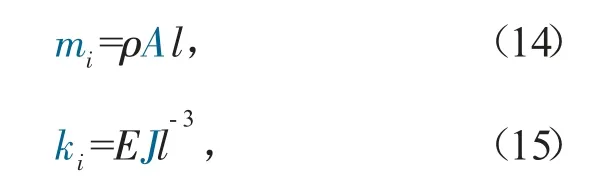
式中：l為機械臂單元長度；ρ、E分別為桿件材料的密度和彈性模量；J、A分別為單元的截面面積和慣性矩。

綜上所述，聯(lián)合式（12）、式（15）可推導出如下關系式為

2.2 不同截面參量對剛?cè)釞C械臂固有頻率影響分析

彈性機構(gòu)常見的幾種截面類型有：實心圓柱、空心圓柱、H型、實心矩形、空心矩形等，具體參數(shù)如表1所示。

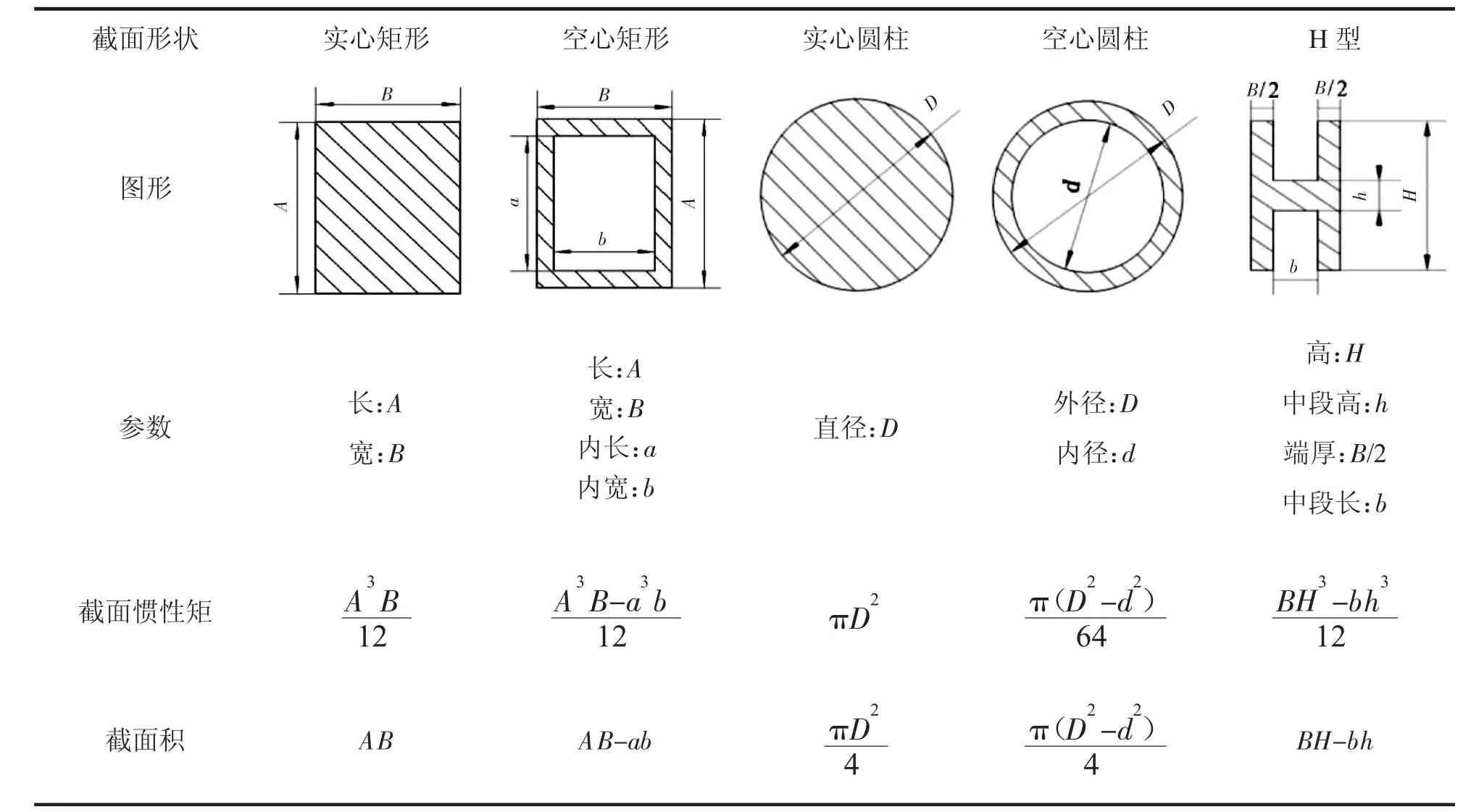
表1 不同截面類型參數(shù)表

相同臂桿長度、相同材質(zhì)的情況下，5種截面機械臂桿件的前兩階系統(tǒng)固有頻率變化規(guī)律如圖2所示。

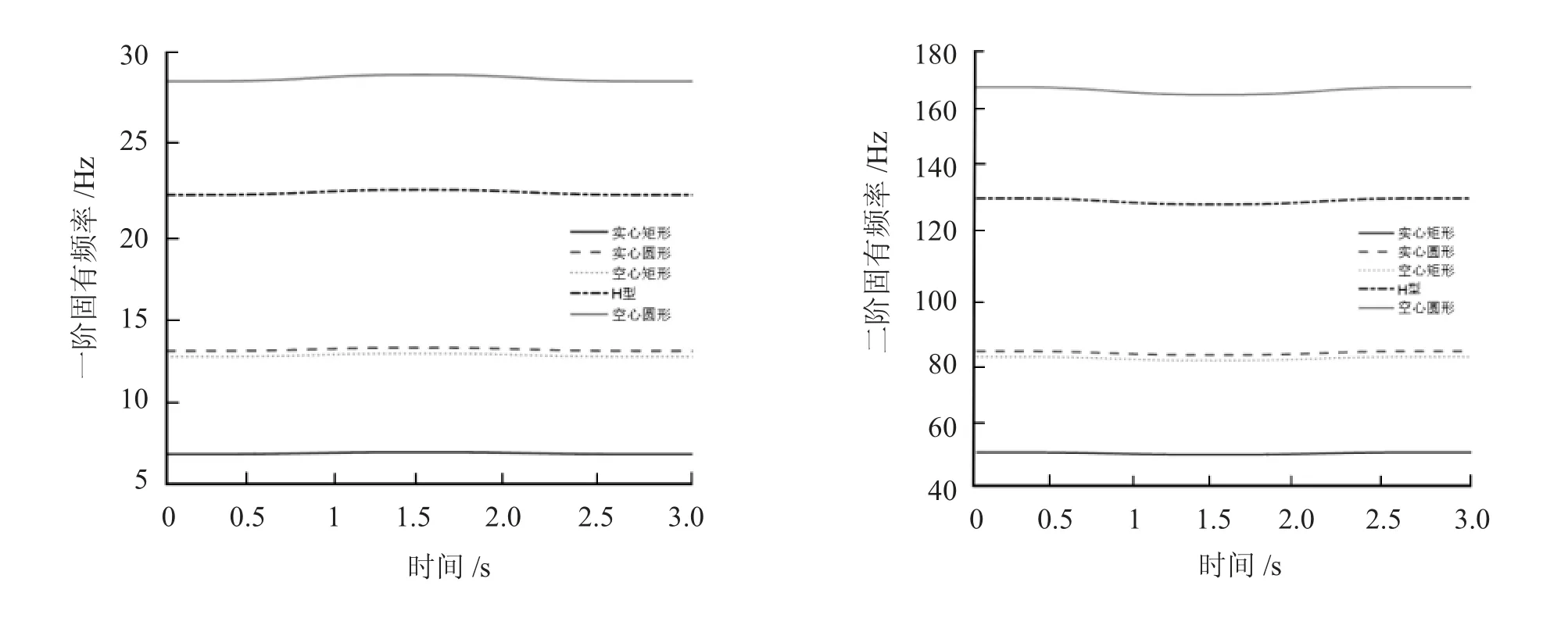
圖2 機械臂固有頻率參數(shù)圖

由圖2可知：截面為實心矩形的剛?cè)釞C械臂固有頻率最低，空心矩形和實心圓形其次，H型再次，空心圓形的固有頻率最高。其中，H型是介于空心和實心之間的一種截面形態(tài)，由圖可以看出，其機械臂各階頻率均較高，且整體曲線較光滑，系統(tǒng)整體穩(wěn)定性較高。因此，筆者選取截面類型為H型的宏柔微剛機械臂來探究其結(jié)構(gòu)、材質(zhì)等參量對其固有頻率特性的影響，為后續(xù)整體優(yōu)化設計提供參考依據(jù)。

2.3 H型宏微機械臂參數(shù)對頻率特性影響分析

定義H型桿件材料為碳鋼，桿件彈性模量E=207 GPa，密度ρ=7 850 kg/m3，柔性機械臂長度L1=1 m，截面寬度B1=45 mm，截面壁厚H1=45 mm，腹板厚b1=10 mm，翼緣厚h1=15 mm；剛性機械臂長度L2=0.5 m，截面寬度B2=6 mm，截面壁厚H2=20 mm，腹板厚b2=6 mm，翼緣厚h2=9 mm。

機械臂關節(jié)角運動規(guī)律為

式中：t0表示運動周期，選取t0=3.0 s。

2.3.1 結(jié)構(gòu)參量對固有頻率的影響

筆者主要從以下兩種方式進行研究：保證剛?cè)釞C械臂長度比值不變，同比改變它們的長度；保證剛?cè)釞C械臂總長度不變，同比改變它們的長度比。通過上面兩種方式進行實驗得到機械臂運動規(guī)律。

1）同比改變剛?cè)釞C械臂的長度。

在保證橫截面積、材料等參量不變的情況下，分別考慮：初始長度、同比增加50%、同比增加100%這3種機械臂宏微桿長度的固有頻率變化規(guī)律，得到如圖3所示前兩階固有頻率變化曲線。

圖3 H型桿件長度比值不變情況下固有頻率參數(shù)變化曲線

由系統(tǒng)前兩階固有頻率變化曲線可以看出：在保證橫截面積、材料等參量不變情況下，隨著H型宏微機械臂桿長的增加，各階固有頻率隨之減小。因此，減少宏微機械臂總體長度有利于提高系統(tǒng)的固有頻率。

2）同比改變剛?cè)釞C械臂的長度比。

保證柔性宏剛性微機械臂的總長度L總=1 500 mm，分別取比值為3：1、5：1、10：1的3種機械臂長度，得到如圖4所示前兩階固有頻率變化曲線。

由圖4可以看出：3種情況下的固有頻率無論一階還是二階都呈現(xiàn)依次遞減的情況，其中，柔性桿件占比越小系統(tǒng)越穩(wěn)定。因此，降低柔性臂桿的占比，有利于提高固有頻率。

圖4 H型桿件長度比值改變情況下固有頻率參數(shù)變化曲線

2.3.2 材質(zhì)參量對固有頻率的影響

前面的研究采用的是碳鋼材料，考慮到鋁材的輕質(zhì)特性，下面將采用碳鋼和鋁材進行搭配分析：全為鋼材料；全為鋁材料；鋼鋁混合（柔性臂采用鋼材料，剛性臂采用鋁材料）。鋁材料的參數(shù)如下：彈性模量E=70 GPa，密度ρ=2 700 kg/m3。3種情況下系統(tǒng)的固有頻率變化曲線如圖5所示。

從圖5變化曲線及各界頻率數(shù)值可知：全鋼和全鋁的柔性宏剛性微機械臂固有頻率比較接近，而“柔性宏鋼+剛性微鋁”這一混合式搭配相比全鋼和全鋁則表現(xiàn)出杰出的性能，其固有頻率遠大于其他2種。這一結(jié)論對于柔性機械臂性能提升具有重要意義。

圖5 H型桿件不同材料情況下固有頻率參數(shù)變化曲線

2.3.3 集中質(zhì)量參量對固有頻率的影響

同理，筆者主要從以下2個角度探究集中質(zhì)量參量對系統(tǒng)固有頻率特性的影響規(guī)律。

1）保證關節(jié)點集中質(zhì)量不變，僅改變末端點集中質(zhì)量。

在保持其他各類影響因素不變或者是相同的情況下，桿件末端加入不同的質(zhì)量：m1=0 kg、m2=1 kg、m3=2 kg，進行實驗仿真得到固有頻率曲線如圖6所示。

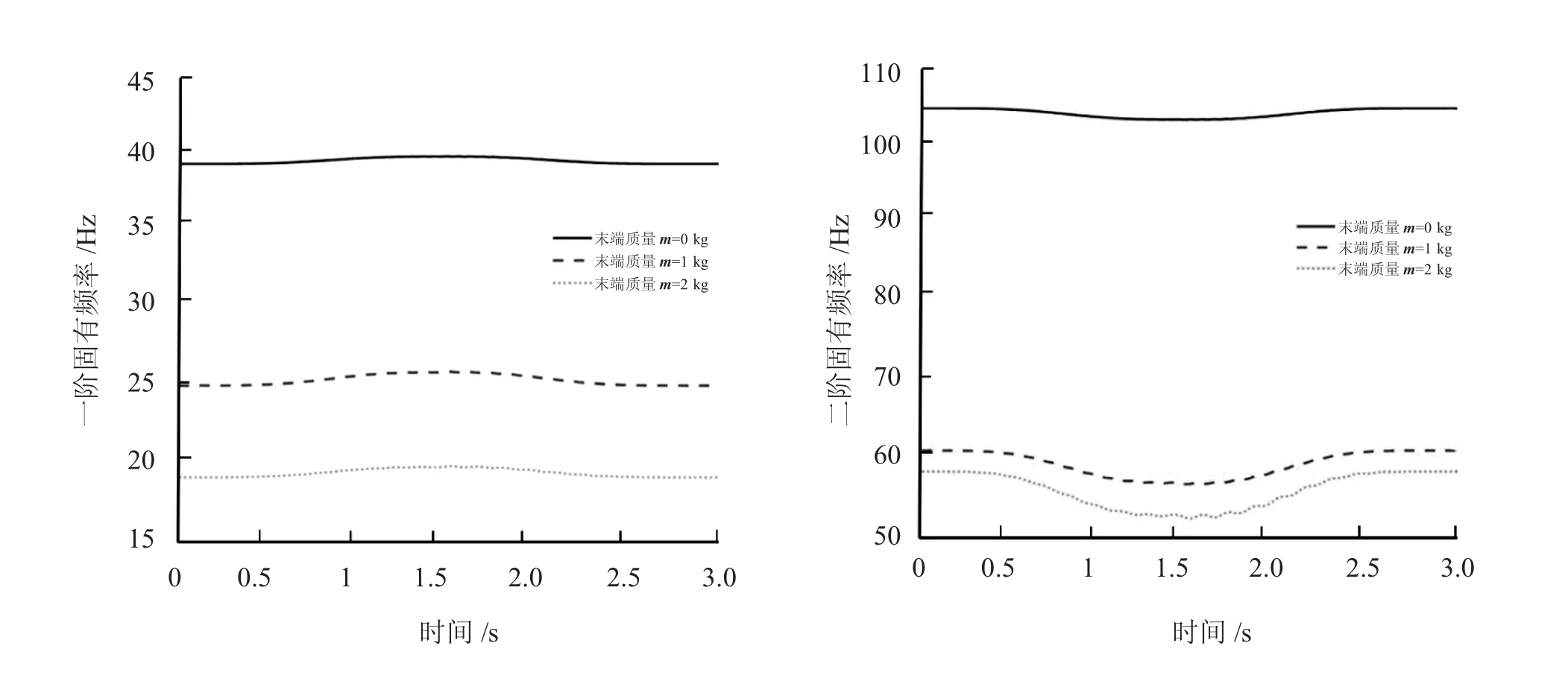
圖6 H型桿件末端添加質(zhì)量情況下固有頻率變化曲線

由圖6可知：隨著末端集中質(zhì)量的逐漸變大，固有頻率逐漸降低。這說明末端集中質(zhì)量對機械臂固有頻率具有較大影響，且成反比關系，降低末端質(zhì)量有利于提高機械臂固有頻率。

2）關節(jié)點和末端點依次增加集中質(zhì)量。

依次在柔性臂的關節(jié)點1、關節(jié)點2及末端點增加1 kg的集中質(zhì)量，即第一次關節(jié)點1處1 kg，第二次關節(jié)點1處1 kg+關節(jié)點2處1 kg，第三次關節(jié)點1處1 kg+關節(jié)點2處1 kg+末端質(zhì)量1 kg。3種情況下固有頻率變化曲線如圖7所示。

圖7 H型關節(jié)點和末端添加質(zhì)量情況下固有頻率變化曲線

由圖7可知：隨著質(zhì)量的逐漸加大，固有頻率逐漸降低，而且其變化呈現(xiàn)較為嚴重的非線性，其中末端質(zhì)量對機械臂動態(tài)特性影響最為嚴重，這是由于末端質(zhì)量距離機械臂基座最遠，其慣性力矩也最大。因此，在不改變宏微機械臂其他參量的情況下，盡量降低微機械臂的質(zhì)量，特別是末端質(zhì)量，可以有效地提高系統(tǒng)的固有頻率。

3 結(jié)論

柔性宏剛性微機械臂作為一種大范圍高速精密機構(gòu)，對其固有頻率特性和內(nèi)在機理進行深入研究具有重要意義。

1）基于有限元法和拉格朗日方程，建立剛?cè)釞C械臂的柔性多體系統(tǒng)動力學模型。

2）研究不同截面剛?cè)釞C械臂固有頻率特性的影響規(guī)律，H型的宏柔微剛機械臂各階頻率均較高，且整體曲線較光滑，系統(tǒng)整體穩(wěn)定性較高。

3）研究發(fā)現(xiàn)：相同外形尺寸情況下，H型剛?cè)釞C械臂不僅質(zhì)量更輕，而且固有頻率更高；隨著等比長度的增加，固有頻率呈現(xiàn)急劇減小趨勢；采用柔性鋼微性鋁機械臂相比全鋼或全鋁，固有頻率大幅提升；在保持其他參量不變的條件下，降低末端質(zhì)量有利于提高機械臂固有頻率。

通過以上分析為進一步研究H型剛?cè)釞C械臂整體優(yōu)化設計提供了理論依據(jù)，對改善剛?cè)釞C械臂系統(tǒng)性能具有重要指導作用。