多策略黑猩猩優化算法研究及其工程應用

黃 倩，劉 升，李萌萌，郭雨鑫

上海工程技術大學 管理學院，上海 201620

黑猩猩優化算法（chimp optimization algorithm，COA）是由Khishe和Mosavi[1]于2020年提出的一種啟發式優化算法。作為一種新型的進化算法，相比于其他群智能算法，COA 除了參數少、易于理解之外，還擁有最重要的兩大特點：一是將種群劃分成獨立個體，模擬其狩獵時的分工行為，而個體的多樣性可以使算法更加徹底的搜索空間以提高算法的勘探能力；二是引入混沌因子來代表黑猩猩在圍獵過程中受到群體激勵而帶來的個體混亂捕獵行為，從而提高了算法在開發階段的收斂速度。

在研究中發現，黑猩猩優化算法（COA）與鯨魚優化算法（WOA）、灰狼優化算法（GWO）的運行原理有一定相通性，但其在收斂精度和收斂速度上又明顯優于兩個算法，因而對黑猩猩優化算法的改進具有很高的研究價值。基本的啟發式優化算法普遍具有易陷入局部最優和收斂精度不高的問題，對此，眾多學者在此類算法的改進策略研究對黑猩猩優化算法在尋優精度和收斂速度上的提升有一定借鑒意義。肖子雅等[2]提出一種基于精英反向學習策略和黃金正弦算法的改進WOA 算法（EGolden-SWOA），在尋優精度上提高了原始算法的性能，但收斂速度上仍有進步的空間。顧清華等[3]提出了一種基于遺傳算法的改進GWO 算法，在提高全局收斂性和收斂精度上取得極大成果。Mohammad等[4]提出了一種基于維度學習的狩獵搜索策略的改進GWO 算法（IGWO），在增強種群多樣性和平衡算法局部和全局搜索上基礎上增強算法的開發能力，但在收斂過程中仍容易陷入局部最優。徐辰華等[5]提出一種將混沌理論與灰狼優化算法結合的Cat 混沌與高斯變異的改進灰狼優化算法，證明了混沌理論在提高算法收斂速度上突出表現。

盡管上述學者在算法的改進中取得了一定成果，但在如何平衡收斂精度和收斂速度上仍有一定不足，因此本文提出一種多策略黑猩猩優化算法（EOSMICOA）。運用無限折疊迭代混沌映射改進精英反向學習策略初始化種群，增加種群的多樣性；利用單純形法提高算法在局部搜索時跳出局部最小值的尋優能力；引入群個體記憶機制提高算法的尋優速度和精確度。通過20個測試函數實驗對比，結果表明，無論在低維和高維實驗，EOSMICOA 在全局尋優的精度以及收斂速度上都表現優秀。最后，通過將EOSMICOA、EGolden-SWOA 與CPSOGSA[6]改進算法應用于焊接梁的復雜工程優化問題上，結果證明EOSMICOA 能更有效地應用于工程實際問題中。

1 黑猩猩優化算法

在黑猩猩群落中，根據個體在狩獵過程中所顯現出的智力和能力的多樣化，對黑猩猩群分類為：驅趕者（Driver）、阻攔者（Barrier）、追捕者（Chaser）和攻擊者（Attacker）。每一類黑猩猩都有自己的獨立思考能力，并用自己的搜索策略探索和預測獵物的位置，他們擁有各自任務的同時，還會由于受到獲得性行為和好處的社會激勵使他們在狩獵的最后階段會出現混亂個體捕獵行為。

黑猩猩優化算法的基本過程如下：假設有N只黑猩猩，第i只黑猩猩的位置為Xi，群體最優解為XAttacker，次優解為XBarrier，第三最優解為XChaser，第四最優解為XDriver。

首先描述黑猩猩接近并包圍獵物的行為，其位置更新公式如下：

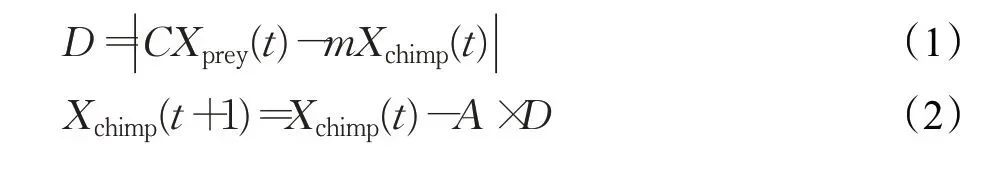
2 多策略黑猩猩優化算法

2.1 混沌反向學習策略初始化種群

由于啟發式優化算法多存在過度依賴種群初始位置的問題，而以隨機方式初始種群會使其分布不均勻，影響算法的求解精度。為此，本文提出一種基于無限折疊迭代混沌映射（Iteration映射）和精英反向學習混合的混沌反向學習策略來對種群初始化，以增加種群的多樣性和質量。混沌運動具有遍歷性和不重復性等特點，所以大多被學者用來生成種群的初始位置，而文獻[7-10]中大多使用的是Logistic映射和Tent映射。通過圖1的4個混沌映射對比，可以發現在1 000次迭代下，Logistic映射生成的混沌變量具有一定的雙峰分布特征，在混沌吸引域的中間分布較為均勻，而兩端分布較為稠密；Tent 映射在0～0.2 的取值范圍內存在小周期現象、容易陷入不動點的問題；Sine映射和Logistic映射類似，在接近0 的底端也存在著分布相對稠密的問題；而相比之下，Iteration映射在0～1的分布最為均勻。為此，本文采用Iteration混沌映射。

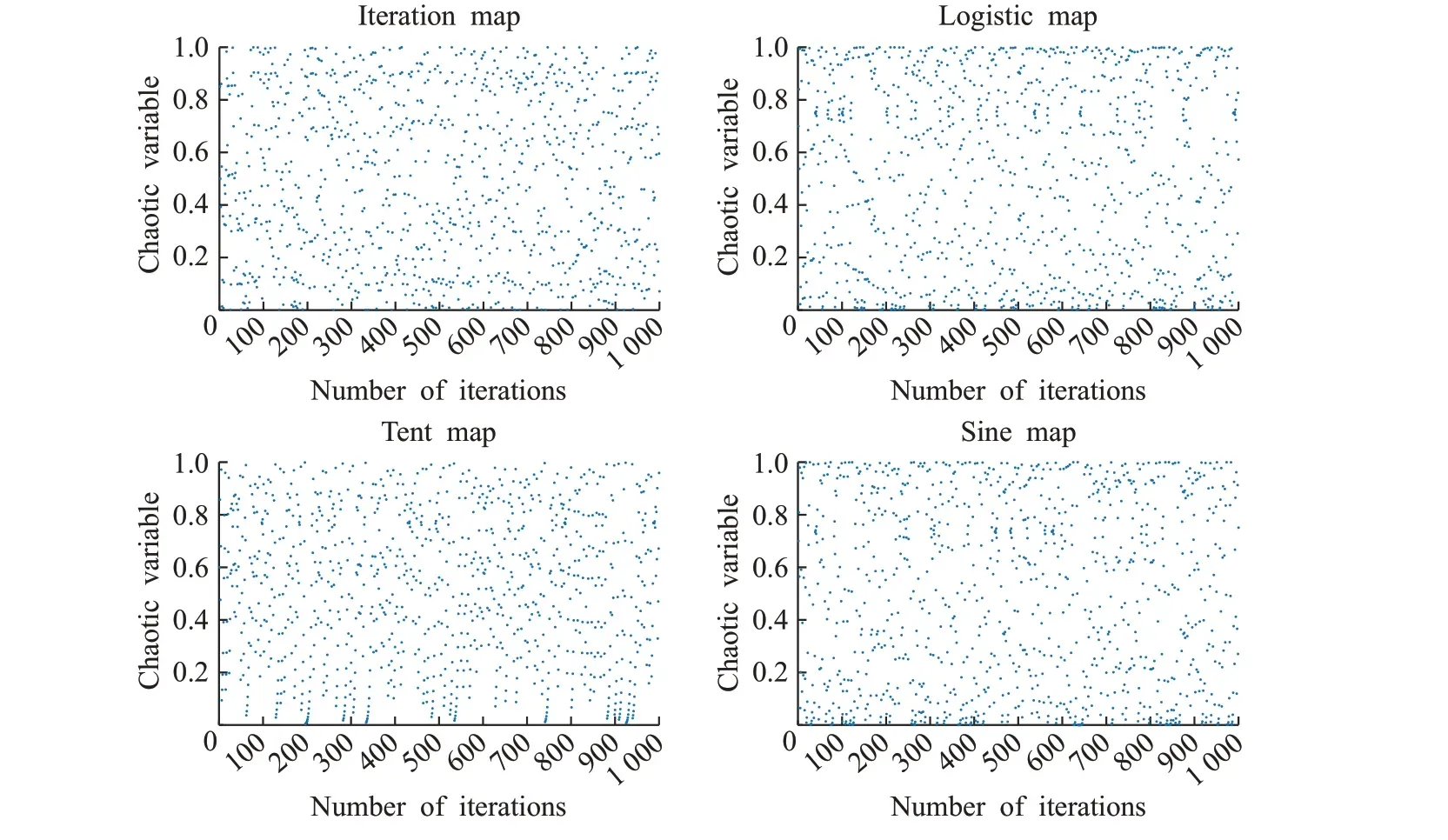
圖1 混沌映射Fig.1 Chaotic map

Iteration映射數學表達式如下：

最后，將混沌生成的所有初始解和混沌精英反向解合并進行排序，選取前N個較優的解作為初始種群。

2.2 單純形法

單純形法是一種不受目標函數連續性和可導性影響的直接搜索算法，其主要通過迭代判斷最差頂點Xs向優運動的方向向量g是否正確，并通過對最差頂點進行反射、擴張、外收縮和內收縮操作來控制其運動。單純形法步驟如圖2所示。

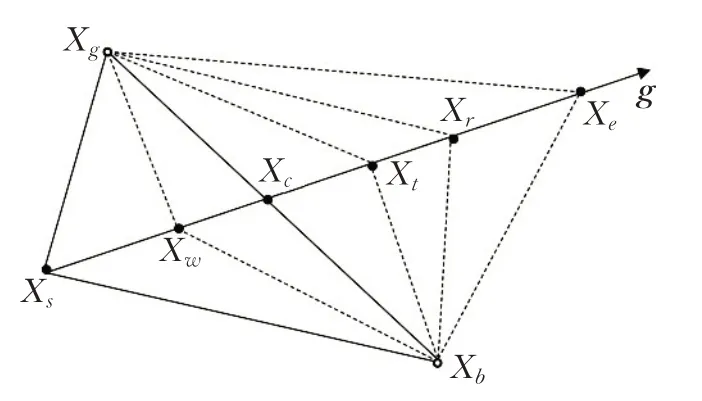
圖2 單純形法示意圖Fig.2 Diagram of simplex method

具體流程如下：

（1）計算種群的適應度值，并將最優的4 個位置分別記為XAttacker、XBarrier、XChaser和XDriver，對應的適應度值為f(XAttacker)、f(XBarrier)、f(XChaser)和f(XDriver)，設中心位置為Xc=(XAttacker+XBarrier)/2。

（2）將剩下黑猩猩個體的適應度值進行排序，選擇適應度值最差的個體作為較差點Xs。

通過運用單純形法的4種操作，可以讓最差點在反射操作下搜索到所有可行的解，內外收縮操作可以使最差點擺脫當前位置，而在擴張操作下可以讓最優解跳出局部最小值，向距離最差點更遠的反方向繼續搜索，從而提高了算法整體的局部開發能力和尋優能力。由于單純形法針對的是種群中最差的個體，對于種群中其他個體仍然執行黑猩猩原始算法中的隨機搜索，故而在提高算法的局部搜索能力的同時，不會降低種群的多樣性。

2.3 群個體記憶機制

在原始COA算法中，通過對群體歷史前4個最優位置的加權記憶，實現了黑猩猩種群間信息交流，最終促使個體在搜索空間快速移動尋優，但這一做法并未考慮到每個黑猩猩個體自身的搜索經驗，因而，在結合COA算法群體信息交流表達式（5）的基礎上，引入粒子群算法的個體記憶策略，具體表達式變為：

其中，b1和b2是[0，1]間的常數，分別表示群體交流和個體經驗記憶的系數；rand表示[0，1]間的隨機變量；Xbest表示第i只黑猩猩所經歷過的最佳位置，Xj,Xi,(j≠i)是記憶過程中記下的隨機個體位置。通過對b1和b2的調節來平衡群體交流和個體記憶對位置更新的影響。

對比原始位置更新方程式（5），式（9）增加了兩個部分：第一個是引入的個體自身記憶信息，進一步提高了算法在局部的開發能力和收斂速度；第二個是隨機記憶的個體位置，從而起到增強算法種群多樣性和全局勘探的能力。

2.4 算法步驟

綜上所述，本文提出EOSMICOA 算法的運算步驟如下：

步驟1 設置相關參數，種群規模N、最大迭代次數tmax、收斂因子f、影響系數A、C、混沌因子m等。

步驟2 利用Iteration 混沌映射和精英反向學習生成初始種群Xi,i=1,2,…,N。

步驟3 計算個體的適應度值，并確定歷史前4個最優解XAttacker、XBarrier、XChaser和XDriver。

步驟4 利用單純形法改變較差個體Xs的位置。

步驟5 更新A、C，按照公式（5）計算其他黑猩猩的位置。

步驟6 通過粒子群算法改進的群個體記憶機制，按照公式（9）進一步更新黑猩猩位置。

步驟7 判斷算法是否達到最大迭代次數，若達到，則算法結束，輸出最優位置XAttacker；否則，執行步驟3。

3 實驗仿真與結果分析

3.1 實驗參數設置

本文選取了COA、WOA、EOSMICOA 和當前最新改進算法EGolden-SWOA、IGWO，在20 個測試函數上進行實驗對比。

以上算法統一參數設置如下：種群規模N為30，最大迭代次數tmax為500，運行次數為30，低維實驗維數為30，高維實驗維數為1 000。

3.2 測試函數

為檢驗EOSMICOA 的優化性能，選取表1 的20 個基準測試函數進行仿真實驗分析，并給出表達式、搜索范圍和最優值，其中f1～f7為7個連續單模態測試函數，用來測試算法的尋優精度，f8～f13為6個連續多模態測試函數，f14～f20為7個固定多模態測試函數，用來測試算法的全局搜索能力和收斂速度。

表1 基準測試函數Table 1 Benchmark functions

3.3 多種啟發式算法比較

3.3.1 算法實驗結果對比

表2、3和表4列出COA、WOA、EOSMICOA、EGolden-SWOA、IGWO 在d=30 和d=1 000 的低維、高維狀態下的7 個單模態和6 個多模態測試函數，以及在7 個固定模態測試函數上分別獨立運行30 次實驗后，得出的最優值、平均值和標準差。其中每個測試函數的最優結果均加粗處理，最優值可以顯示出算法的尋優能力，平均值可以用來反映算法總體所能達到的收斂精度，標準差則反映出算法的魯棒性和穩定性。

從表2的低維單模態測試函數的比較結果可知，總體看，無論是在低維30維還是高維1 000維上EOSMICOA在f1～f7這7 個測試函數上均顯現出最好的尋優能力。對于f1、f3，EOSMICOA的尋優性能最好，甚至可以直接尋到最優值0，在f2、f4上，EOSMICOA 的平均尋優精度均在10-200以上，且EOSMICOA在這4個函數上的標準差均為0，說明EOSMICOA 不論高維還是低維，算法的穩定性和魯棒性都同樣良好；其次，是改進算法EGolden-SWOA的尋優能力，在f1～f7函數上也表現出優良的尋優效果，甚至在低維情況下的f1和f3，可以直接收斂到最優值，在低維的f4、f5、f7的平均尋優精度僅次于EOSMICOA，甚至在低維的f5、f7上可以達到幾個算法最高的精度，但標準差卻高于EOSMICOA，但是，在高維實驗中的表現依然劣于EOSMICOA；其次表現較好的是標準COA 算法，其尋優效果和算法的穩定性在f1～f7函數上均比改進算法IGWO 要好，可見標準COA 算法在算法的設計上具有一定優越性，而對COA的改進研究也更具有重大意義。最后表現較好的是IGWO，除了低維的f1、f2實驗上的尋優精度比不過WOA，但在高維實驗中，IGWO 的表現比較穩定，在剩下的f3、f4、f5、f6、f7中的高、低維實驗中均比WOA的尋優效果理想，而WOA的表現相對較差。

表2 單模態測試函數實驗結果Table 2 Experimental results of single mode test functions

從表3的多模態測試函數的實驗結果比較可知，在f8～f13函數的高維和低維實驗中上，EOSMICOA 依然表現出不同尋常的尋優能力。尤其是在f9～f11函數上，EOSMICOA 的尋優精度極佳，可以直接尋到最優值0，在f10、f12、f13的高、低維實驗上，EOSMICOA最優值、平均值和標準差均是4個算法最小的，說明EOSMICOA在多模態測試函數高、低維實驗上上仍然具有相對最優良的尋優能力和算法穩定性；其次，表現優良的是改進算法EGolden-SWOA，在f8上的最優值是幾個算法中的最優結果，但其標準差也最大，在f9、f10、f11這3個函數上可以和EOSMICOA 一樣達到最優結果；接著，表現最好的是IGWO，在f9、f10、f11函數上，IGWO 在高維實驗的尋優能力和穩定性甚至比在低維實驗上的要好，可以從中發現IGWO 比起低維函數，更適合用于高維函數問題，在剩下的4個函數中的尋優表現均要勝于標準的COA和WOA算法；最后，WOA在f8～f13的低維和高維實驗中，尋優精度和穩定性均比COA要好，甚至在f9、f11兩個函數的高、低維實驗上的最優值均可以和EOSMICOA 一樣直接收斂到0，而相對其他幾個算法在多模態測試函數上實驗結果而言，COA 的表現最差。

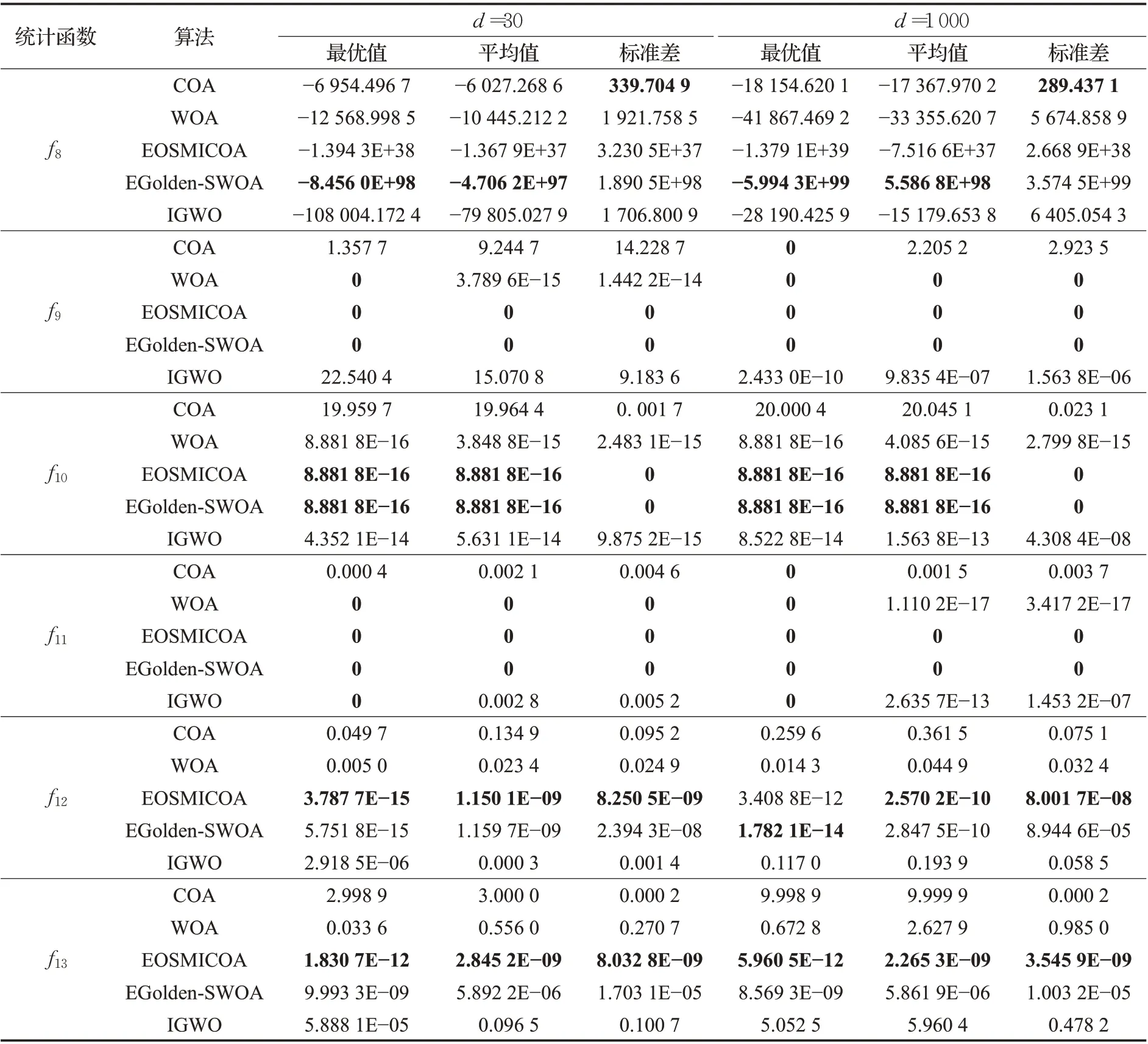
表3 多模態測試函數實驗結果Table 3 Experimental results of multimodal test functions

在表4固定多模態測試函數的實驗結果對比中，可以發現EOSMICOA在7個固定模態的測試函數上的尋優精度都達到了最高，在前面13 個復雜函數的高維實驗中表現不好的IGWO 在這7 個固定模態的測試函數上的表現也發生變化，擁有較高的算法穩定性，而EGolden-SWOA的表現則位列第三。

表4 固定多模態測試函數實驗結果Table 4 Experimental results of fixed multimode test functions

EOSMICOA、EGolden-SWOA、IGWO 這3 個算法在f15、f16、f18和f20中都直接收斂到最優值0.000 3、-1.031 6、3.000 0和-10.153 2，但相比之下IGWOA的標準差在f16、f18上最小，而EOSMICOA在f15、f20的標準差最小，說明IGWO 和EOSMICOA 的穩定性和魯棒性都較好；在f14、f17、f19中，EOSMICOA 均獲得了幾個函數中的最佳精確度，在f14上的標準差也最小；顯然，表現較好的IGWO和EGolden-SWOA在算法的穩定性和尋優能力上各有千秋，IGWO擁有較高的算法穩定性，而EGolden-SWOA的收斂精度要高于IGWO；最后，標準COA 和WOA 在固定模態測試函數的實驗中表現最弱。

通過EOSMICOA、EGolden-SWOA和IGWO這3個改進算法在13 個單模態、多模態復雜函數的高維實驗和7個固定模態函數的實驗對比中，可以發現EOSMICOA的尋優精度最佳，且迭代和運行過程中表現出優秀的穩定性和魯棒性。盡管在部分函數上，EGolden-SWOA和IGWO 也可以收斂到函數最優值，但根據圖3 的5個函數收斂圖可以發現，EOSMICOA 尋到最優值所需要的迭代次數均小于EGolden-SWOA，在f1和f3上，EOSMICOA 尋優需要迭代的次數甚至比EGolden-SWOA少100次，比IGWO則少300次；在f9、f10、f11上，EOSMICOA尋優需要迭代的次數比EGolden-SWOA 少至少50次，比IGWO則少200次。

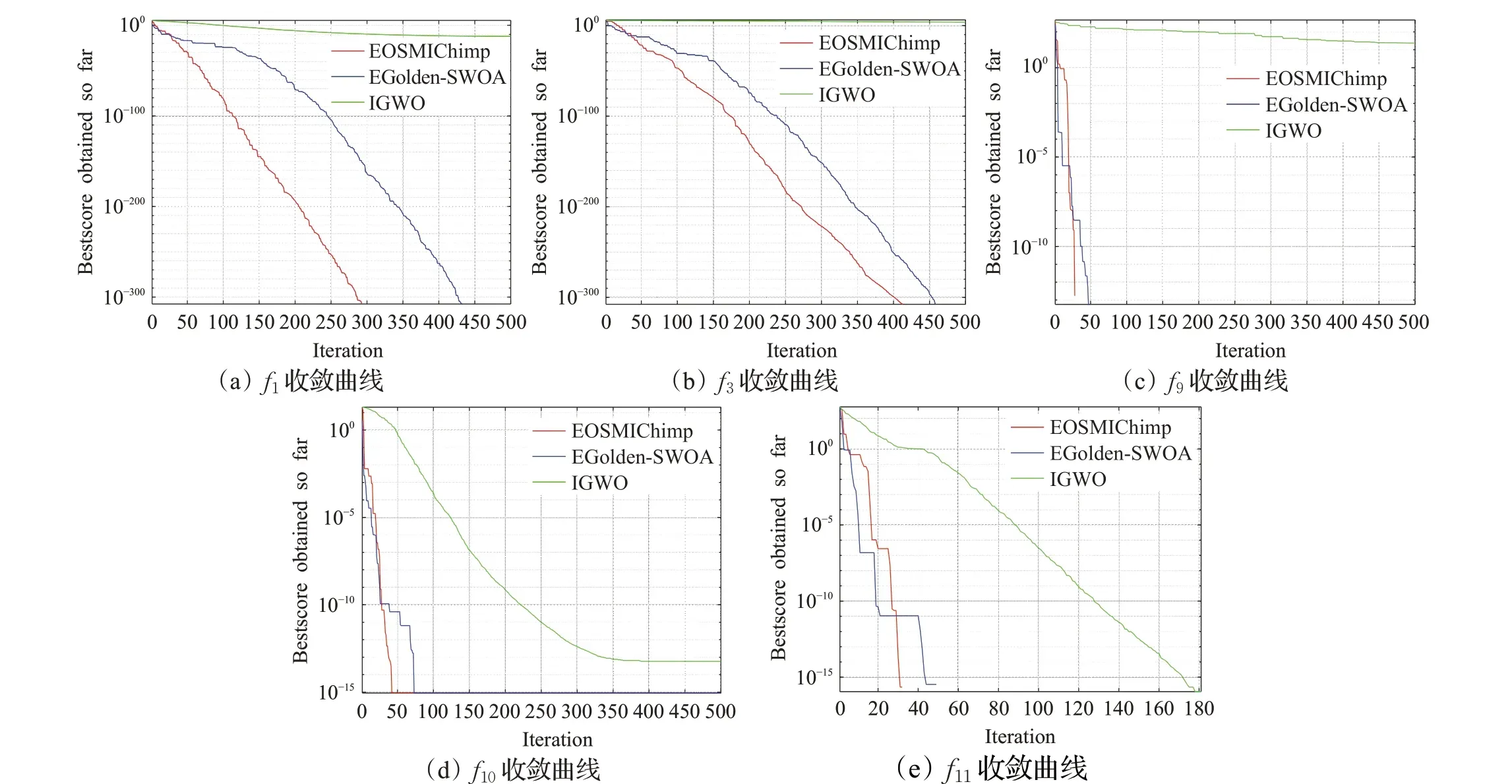
圖3 函數收斂圖Fig.3 Function convergence diagram

綜上表明，EOSMICOA 除了取得較高的收斂精度以外，更在收斂速度上有較大的提高，這歸功于改進策略中的單純形法和群個體記憶機制。單純形法通過運用4 種操作改變最差個體的位置并不斷更新最差個體的方法來提高算法跳出局部最優解的能力，但并不能大幅提高算法整體的收斂速度，由此，加入的群個體記憶機制可以將最優位置信息成功地傳遞給下一代個體并記錄下來，從而減少搜尋較差解的時間，大大加快了算法的尋優速度，同時記憶過程中記下的隨機個體位置也可以使算法在后期保持良好的種群多樣性，起到了平衡算法在局部開發和全局勘探能力的重要作用。

3.3.2 時間復雜度分析

EOSMICOA 主要由Iteration 映射和精英反向學習結合的混沌反向學習策略初始化種群、單純形法和群個體記憶機制等操作組成。當算法的種群規模維N，問題維度維d，最大迭代次數為tmax，每個操作的時間復雜度如下：混沌反向學習策略初始化種群的復雜度為O( (N+N×d)×tmax)，單純形法的復雜度為O(N×tmax)，而群個體記憶機制的復雜度為O(N×d×d×tmax)，EOSMICOA 整體復雜度為O(tmax×N×d×d)，而COA和WOA 的復雜度為O(tmax×N×d)，EGolden-SWOA的復雜度為O(tmax×N×d×d)，IGWO 的復雜度同樣為O(tmax×N×d)。因此相比幾個算法，EOSMICOA和EGolden-SWOA 的時間復雜度相同，而比標準COA、WOA和IGWO高，但也在可以接受的范圍內。

4 EOSMICOA算法的焊接梁設計應用研究

為驗證EOSMICOA 在解決實際問題中的有效性，將其應用于機械設計中的復雜優化問題，即焊接梁最小費用問題，其設計原理示意圖如圖4所示。

圖4 焊接梁設計原理Fig.4 Design principle of welded beam

焊接梁設計問題的目標是使其制作成本最小，圖4為焊接梁設計圖，其約束變量為剪切應力τ，梁彎曲應力σ，桿曲載荷Pc和梁端撓度δ，此設計問題所需要優化的變量為焊縫厚度h、夾條長度l、梁長t和梁寬b，這4個優化變量的目標函數和約束條件如下：

分別利用EOSMICOA 算法、EGolden-SWOA 算法和CPSOGSA算法進行求解，參數設置相同，3種算法分別運行30次求解結果的最優值、平均值和標準差如表5所示，圖5 為3 種改進算法求解焊接梁設計問題的收斂曲線。

從表5 的對比結果，可以清楚地發現，在求解焊接梁工程設計這一復雜優化問題時，EOSMICOA 的表現最佳，其設計出的焊接梁成本最優情況下可以達到1.695 6，遠低于EGolden-SWOA 和CPSOGSA 的最優值，且總體平均也要優于其他兩個改進算法；雖然從求解結果的穩定性來看，EOSMICOA 的標準差要高于EGolden-SWOA，但相差并不太大，且仍然比CPSOGSA的標準差要低。從圖5的3種算法的求解結果收斂曲線也可以發現，EOSMICOA的收斂速度是3種改進算法中最快的，在200次迭代后就基本尋到最優值，而EGolden-SWOA和CPSOGSA在500次的迭代內無法收斂到比較好的結果。

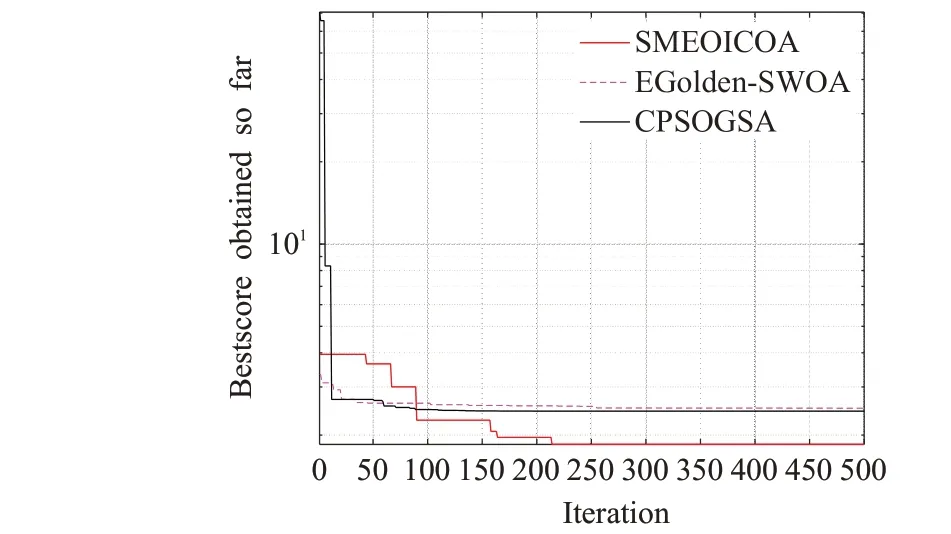
圖5 焊接梁設計問題求解結果收斂曲線Fig.5 Convergence curve of solution result of welding beam design problem

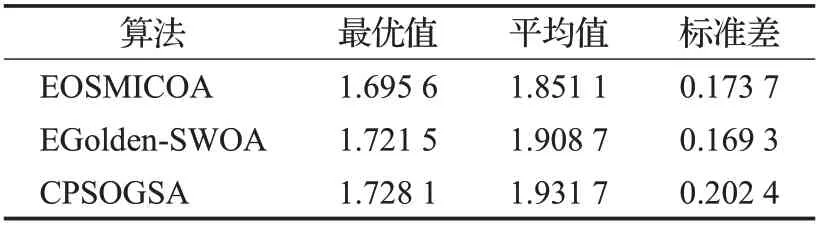
表5 焊接梁設計問題3種算法求解結果對比Table 5 Comparison of three algorithms for welding beam design

5 結束語

本文針對原始黑猩猩優化算法存在的依賴初始種群、收斂精度不高、容易陷入局部最優等問題，提出來一種多策略黑猩猩優化算法：EOSMICOA。利用無限折疊迭代混沌映射（Iteration映射）和精英反向學習策略的結合初始化種群，并應用單純形法和群個體記憶機制改進個體的位置，使得原始算法在提高尋優精度的同時大大提高收斂速度，也為進一步改進啟發式優化算法提供新的改進優化策略方案。EOSMICOA這一改進策略的效果，通過在13 個復雜測試函數的低維和高維實驗以及7 個固定多模態復雜函數上與多種算法的比較中得以展現，但EOSMICOA在面對函數f5～f7、f12時，仍有進一步提升收斂精度的空間。同時，將EOSMICOA 應用于焊接梁設計這一復雜工程優化問題中也得到比較好的結果，說明改進的EOSMICOA 在實際工程問題中也具有良好的適用性。下一步的研究內容將考慮繼續提升EOSMICOA 算法在全局尋優的能力，并將其與深度學習結合起來應用于現實問題中。