三支面向屬性概念格的規則提取

賀曉麗，柳戰英，錢 婷

1.西安石油大學 理學院，西安 710065

2.西北大學 概念認知與智能研究中心，西安 710127

3.西安石油大學 計算機學院，西安 710065

形式概念分析是德國數學家Wille[1]于1982 年提出的一種數據分析理論，其中形式概念與概念格是形式概念分析的基礎。作為數據分析和知識處理的一種有效工具，形式概念分析在數據挖掘、機器學習和信息檢索等領域有著廣泛的應用。

形式概念分析與其他理論相結合，產生了一系列概念格的模型。Duntsch和Gediga[2]把粗糙集中的上、下近似引入到形式概念分析之中，提出了面向屬性的形式概念。類似地，Yao[3]給出了面向對象概念的定義并研究了它的一些性質。針對部分對象屬性值缺失這一現象，Burmeister等[4]進一步提出了不完備形式背景，并研究了基于不完備信息的概念分析及知識獲取。Li等[5]在不完備形式背景中定義了近似概念并研究了近似概念格的構造、規則提取與屬性約簡。Belohlavek[6]定義了一對模糊伽羅瓦連接并研究了相應的性質，進而給出模糊概念的刻畫。與三支決策思想相結合，祁建軍等提出了三支概念格，進一步研究對象（屬性）誘導的三支概念格與經典概念格之間的聯系[7-8]。Qian等[9]通過將原背景與其補背景并置（疊置）給出三支概念格的構造。劉琳等[10-11]給出了屬性（對象）導出三支概念格的規則提取的方法，并研究了所獲的規則與經典形式背景下規則的內在聯系。Wei等[12]利用置信度探討了屬性導出三支概念格的規則提取方法和非冗余規則的性質。王一賓等[13]通過合并對象導出三支概念格和屬性導出三支概念格，給出相應的規則提取算法。Ren等[14]探討了三支概念格的四種約簡理論。Li 等[15]基于不完備形式背景研究了三支近似概念的約簡理論。而三支概念刻畫了對象和屬性之間的“共同具有”和“共同不具有”關系，為了刻畫對象和屬性之間的“局部完全共有”和“局部完全不共有”的關系，Wei和Qian[16-17]提出了三支面向屬性（對象）概念，并給出了三支面向屬性（對象）概念格的構造方法。

規則提取是形式概念分析的主要目的之一，也是該領域的重要研究課題。近年來，已有一系列相關研究成果。例如，張文修等[18]將決策規則的概念引入到形式概念分析之中。為了提升決策規則對于決策分析的有效性，Li 等[19-20]提出了一種從形式背景之中獲取所有非冗余決策規則的方法和知識約簡理論。Qu等[21]首次引入了決策形式背景中的決策蘊涵。Wu等[22]細致研究了形式背景中的粒規則。Ren等[23]通過使用面向屬性和面向對象的概念格，提出了兩種不同的決策規則。然而，基于基于由面向屬性概念和面向對象概念所導出決策規則的屬性約簡還沒有得到深入研究，Qin 等[24]在此方面做了較為深入的研究，得到了諸多有趣的結論。已有這些研究對基于三支面向屬性概念格的決策規則未有涉及，而三支面向屬性概念刻畫了對象和屬性之間的“局部完全共有”和“局部不完全共有”關系，相應的決策規則語義更為豐富，表達更為精細。本文正是鑒于此考慮，在文獻[16-17]基礎上，首先給出決策形式背景的兩種協調性的定義（P-協調和AEP-協調），進一步探討了兩種協調性之間的聯系；其次，研究了三支面向屬性概念格的規則提取方法和非冗余規則的刻畫，并給出獲取三支面向屬性概念非冗余規則的算法；最后，從原背景和補背景兩種角度，討論了三支面向屬性規則與面向屬性規則之間的內在聯系。

1 基礎知識

定義1[2-3]設(U,A,I)為一形式背景，且2U與2A之間的一對算子定義如下：對于任意的X?U,B?A：

稱LP(U,A,I)為(U,A,I)的面向屬性概念格。

例1 表1是一個形式背景(U,A,I)，對象集U={1,2,3,4,5}，條件屬性集A={a,b,c,d,e}，該背景的面向屬性概念格LP(U,A,I)如圖1所示。

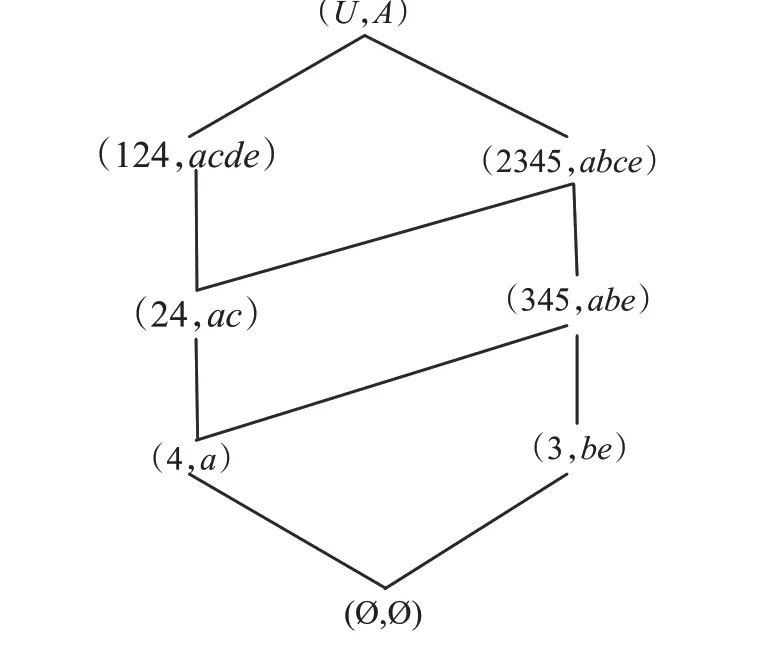
圖1 面向屬性概念格LP(U,A,I)Fig.1 Property oriented concept lattice LP(U,A,I)

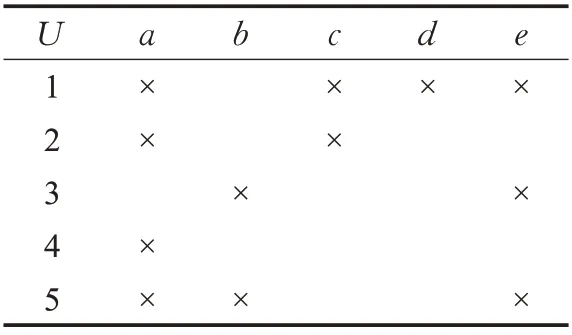
表1 形式背景(U,A,I)Table 1 Formal context(U,A,I)

可以將上述定義的算子推廣為一對負算子。

定義2 設(U,A,I)為一形式背景，且2U與2A之間的一對負算子定義如下：

對于任意的X?U,B?A：

定義4[16]設(U,A,I)為一形式背景，?X,Y?U且B?A，由屬性誘導的三支面向屬性算子分別定義如下：?:2A→2U×2U，?:2U×2U→2A，其中B?=(B□,B-□)且(X,Y)?=X?∪Y?。

若B?=(X,Y),(X,Y)?=B，則稱((X,Y),B)為由屬性誘導的三支面向屬性概念。(U,A,I)上所有的三支面向屬性概念構成之集為LAEP(U,A,I)。在LAEP(U,A,I)上定義二元關系“≤”如下：對于任意的((X,Y),B),((Z,W),C)∈LAEP(U,A,I),((X,Y),B)≤((Z,W),C)?X?Z且Y?W?B?C，不難驗證≤為偏序關系且(LAEP(U,A,I),≤)構成一個完備格，稱LAEP(U,A,I)為三支面向屬性概念格。

任意兩個三支面向屬性概念((X,Y),B)，((Z,W),C)的上確界和下確界為：

((X,Y),B)∨((Z,W),C)=(((X,Y)∪(Z,W))??,B∪C)

((X,Y),B)∧((Z,W),C)=((X,Y)∩(Z,W),(B∩C)??)

將三支決策思想與面向屬性概念結合可以得到三支面向屬性概念，三支面向屬性概念可以精確的刻畫局部完全共有與局部完全不共有的含義。

引理1[17]設(U,A,I)為一形式背景，(U,A,Ic)為其補背景，其中Ic=(U×A)I，若(X,B)∈LP(U,A,I)及(Y,C)∈LP(U,A,Ic)，則((X,B-□),B)∈LAEP(U,A,I)且((C□,Y),C)∈LAEP(U,A,I)。

引理2[17]設(U,A,I)為一形式背景，(U,A,Ic)為其補背景，其中xIc=(U×A)×I，若((X,Y),B)∈LAEP(U,A,I)，則(X,X?)∈LP(U,A,I)且(Y,Y?)∈LP(U,A,Ic)。

引理3[17]設(U,A,I)為一形式背景，(U,A,Ic)為其補背景，其中Ic=(U×A)I，則：

（1）存在LP(U,A,I)到LAEP(U,A,I)的保并序嵌入；（2）存在LP(U,A,Ic)到LAEP(U,A,I)的保并序嵌入。

2 三支面向屬性概念格的規則提取

下面給出三支面向屬性概念的AEP-協調性、AEP-規則和相應的非冗余規則的定義。

定義5 設(U,A,I,D,J) 是一個決策形式背景，LAEP(U,A,I)和LAEP(U,D,J)分別為由條件屬性和決策屬性導出的三支面向屬性概念格，若對于任意的((Z,W),C)∈LAEP(U,D,J)，存在((X,Y),B)∈LAEP(U,A,I)，使得(X,Y)=(Z,W)（即，X=Z,Y=W），則稱LAEP(U,A,I)細于LAEP(U,D,J)，記為：

LAEP(U,A,I)≤LAEP(U,D,J)

相應地，稱形式背景(U,A,I,D,J)是三支面向屬性協調的，簡稱AEP-協調的。

例2 表2 是一決策形式背景(U,A,I,D,J)，對象集U={1,2,3,4}，條件屬性集A={a,b,c,d,e,f}，決策屬性集D={g,h,k}，該背景的三支面向屬性概念格LAEP(U,A,I)和LAEP(U,D,J)分別如圖2和圖3所示，顯然LAEP(U,A,I)≤LAEP(U,D,J)。

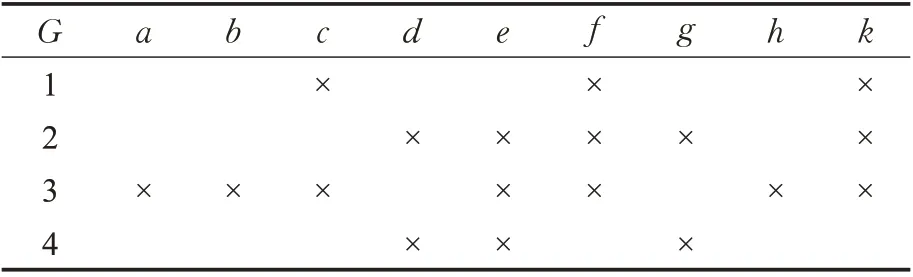
表2 決策形式背景(U,A,I,D,J)Table 2 Decision formal context(U,A,I,D,J)

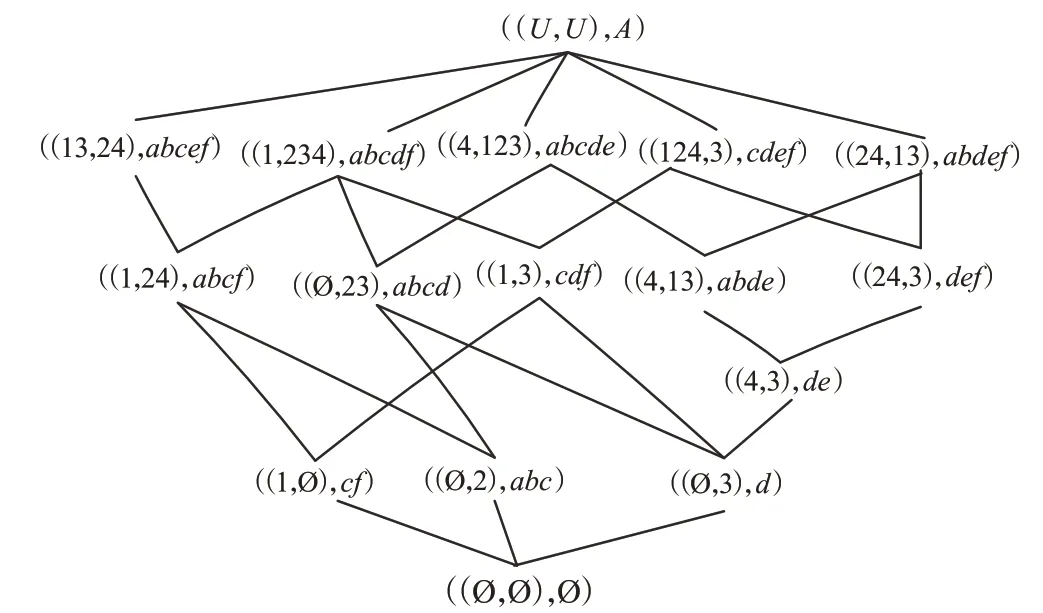
圖2 三支面向屬性概念格LAEP(U,A,I)Fig.2 Three-way property oriented concept lattice LAEP(U,A,I)

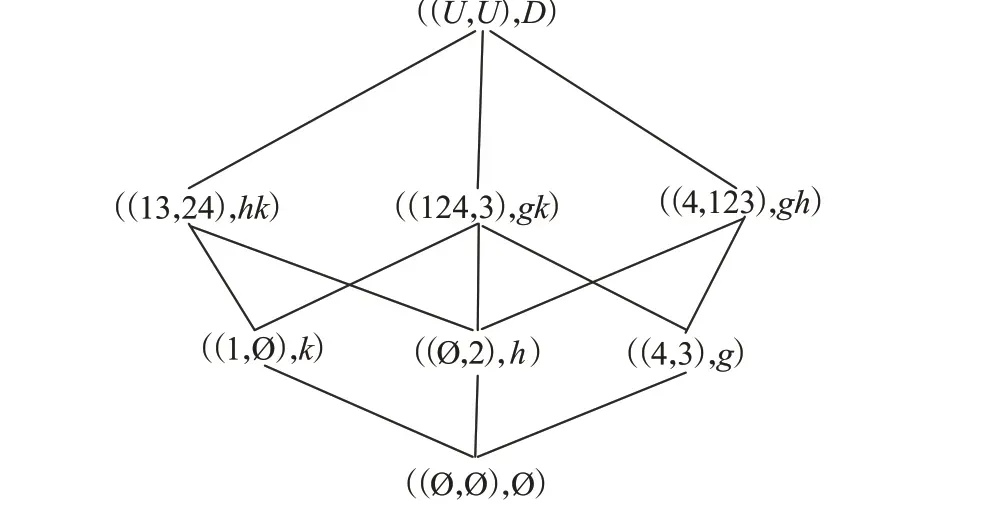
圖3 三支面向屬性概念格LAEP(U,D,J)Fig.3 Three-way property oriented concept lattice LAEP(U,D,J)

定義6 設(U,A,I,D,J)是AEP-協調的決策形式背景，若對于(X,Y),(Z,W)≠(?,?),(U,U)，((X,Y),B)∈LAEP(U,A,I)，((Z,W),C)∈LAEP(U,D,J)，滿足(X,Y)?(Z,W)（即，X?Z,Y?W），則稱B→C是一個三支面向屬性決策規則，簡稱為AEP-規則，記為IfB，thenC。以下用?AEP表示決策形式背景(U,A,I,D,J)上所有的AEP-規則的集合。

由B?=(X,Y)?(Z,W)=C?知，對于任意的(x,y)∈(X,Y)，如果x局部完全共有屬性集B，則x局部完全共有屬性集C；且y局部不完全共有屬性集B，則y局部不完全共有屬性集C。三支面向屬性概念格比面向概念格蘊含的信息多，不僅反映了對象局部完全共有的屬性，而且也能反映對象局部不完全共有的屬性，因此，所定義的三支面向屬性決策規則不僅給出規則的正信息，而且給出了規則的負信息，使得所獲取的規則語義更加豐富。

定義7 設決策形式背景(U,A,I,D,J)是AEP-協調的，對于任意兩個三支面向屬性決策規則B→C和B′→C′，若其滿足條件B?B′,C′?C，則稱規則B→C蘊含規則B′→C′，記B→C?B′→C′，并稱規則B′→C′是冗余的。

定理1 設(U,A,I,D,J)為一決策形式背景，((X,Y),B)∈LAEP(U,A,I) ，((Z,W),C)∈LAEP(U,D,J) ，B→C∈?AEP，則B→C是冗余的當且僅當αP((X,Y),(Z,W))=0或βP((X,Y),(Z,W))=0；則B→C是非冗余的當且僅當αP((X,Y),(Z,W))=1 且βP((X,Y),(Z,W))=1。

例3（續例2）決策形式背景(U,A,I,D,J)的三支面向屬性規則之集?AEP和相應的非冗余規則之集?*AEP如表3所示。

表3 三支面向屬性規則之集?AEP 和非冗余規則之集?*AEPTable 3 Three-way property rules ?AEP and non-redundant three-way rules ?*AEP

下面研究三支面向屬性概念格與面向屬性概念格的規則之間的內在聯系。

定義8 設(U,A,I,D,J)是一個決策形式背景，?(Y,C)∈LP(U,D,J)，?(X,B)∈LP(U,A,I)，使得X?Y，則稱LP(U,A,I)細于LP(U,D,J)，記作LP(U,A,I)≤LP(U,D,J)，簡稱決策形式背景(U,A,I,D,J)是P-協調的。

定義9 設(U,A,I,D,J)是一個決策形式背景，且滿足LP(U,A,I)≤LP(U,D,J)，如果對于(X,B)∈LP(U,A,I)，存在(Y,C)∈LP(U,D,J)，滿足X?Y（其中，X≠?且Y≠U），則稱B→C為一面向屬性規則，所有面向屬性規則之集記為?P。

這個定理說明在面向屬性概念規則中，可以找到更少的規則。

例4 表2的面向屬性概念格LP(U,A,I)和LP(U,D,J)分別如圖4和5所示，顯然LP(U,A,I)≤LP(U,D,J)，表4給出了形式背景(U,A,I,D,J)的面向屬性規則，容易驗證?P??AEP。

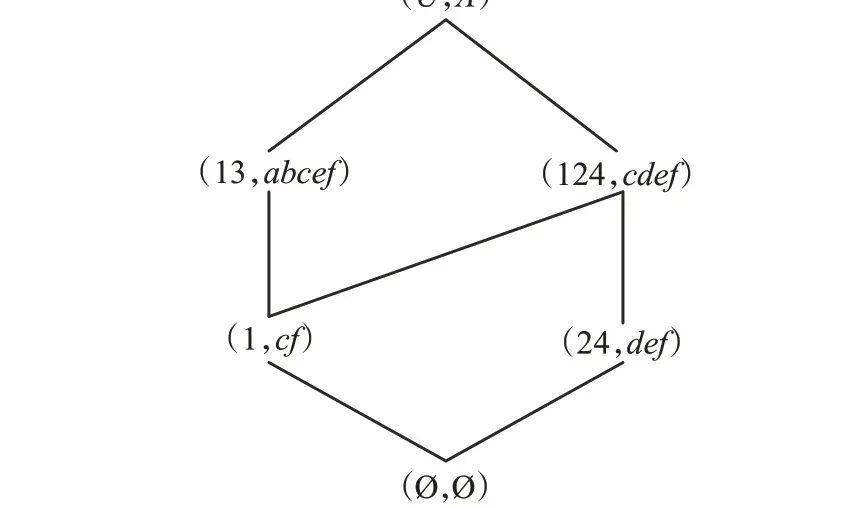
圖4 面向屬性概念格LP(U,A,I)Fig.4 Property oriented concept lattice LP(U,A,I)

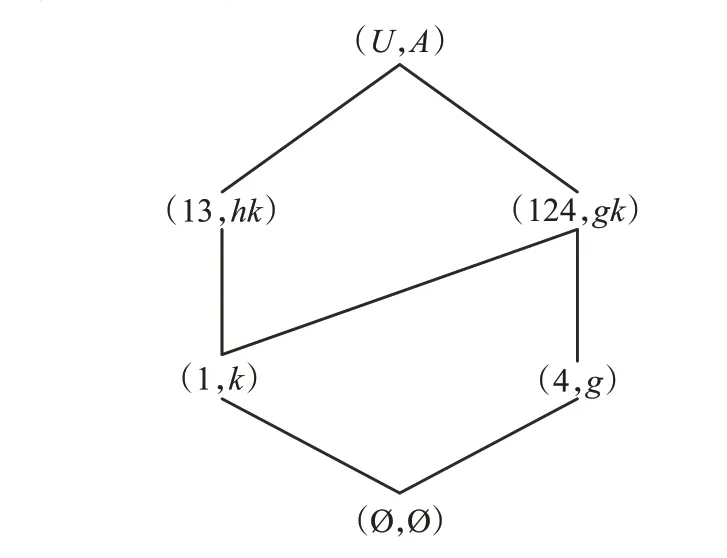
圖5 面向屬性概念格LP(U,D,J)Fig.5 Property oriented conceptlattice LP(U,D,J)

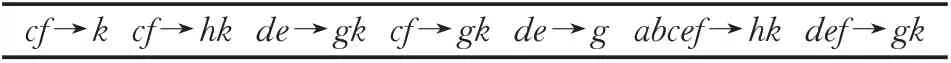
表4 形式背景(U,A,I,D,J)的面向屬性規則集?PTable 4 Property oriented rules ?P of formal context (U,A,I,D,J)

3 基于決策形式背景的補背景的兩種屬性規則的比較

在本章中，基于決策形式背景的補背景，進一步研究了面向屬性規則和三支面向屬性規則之間的區別與聯系，探討了規則提取與背景協調性之間的內在聯系。

所以，LP(U,A,Ic)≤LP(U,D,Jc)。

定理7 設(U,A,I,D,J) 是一個決策形式背景，且LAEP(U,A,I)≤LAEP(U,D,J)，對于任意的B1→C∈?cP，總存在B2→C∈?AEP滿足B1?B2。

4 總結與展望

將三支決策思想引入到面向屬性概念格中，得到三支面向屬性概念格，在細于關系下定義了三支面向屬性的規則和相應的冗余規則并給出非冗余規則的刻畫和算法；其次，研究面向屬性規則與三支面向屬性規則之間的內在聯系及協調性之間的關系，最后，在決策形式背景的補背景中，得到相應的三支面向屬性概念規則，可以豐富三支面向屬性概念規則的獲取理論。本文只考慮協調性下的三支面向屬性規則提取，還可以進一步考慮非協調下的三支面向屬性規則獲取的方法及三支面向對象規則獲取的方法和聯系。