EMS型高速磁浮列車 - 橋共振分析

李貽材

(中鐵十一局集團第一工程有限公司， 湖北 襄陽 441104)

磁浮列車 - 橋梁耦合振動系統中包含車輛子系統、橋梁子系統、控制子系統和軌道不平順，是一個電能、機械能相互轉換的復雜系統。國內外對磁浮車 - 橋耦合振動特性進行了大量研究。Zhao等[1]對高速磁懸浮列車隨機振動和行走質量進行了分析。Han等[2]研究了中低速磁懸浮列車橋耦合振動。武建軍等[3]分析了EMS磁浮列車/多跨簡支梁橋梁系統的動力學特性。滕延鋒等[4,5]對磁懸浮列車在三跨連續梁上通過時軌道的振動反應進行了數值仿真。Yau[6～8]對神經網絡PI控制下的簡化磁懸列車橋耦合振動進行了研究。Kong等[9]對比了懸浮列車分別采用反饋控制、線性二次高斯控制(LQG)和滑模控制(SMC)的車橋振動。時瑾等[10]探討了隨機不平順激勵下磁浮車輛軌道梁的動力響應。周勁松等[11]利用虛擬激勵分析了磁浮車輛運行平穩性。

以上文獻中分別對不同系列磁浮列車、不同類型橋梁、不同控制方法和軌道不平順下的車橋耦合振動進行了研究，但都沒有涉及促使磁懸浮列車產生共振的行車速度和自振頻率，以及簡支梁橋對磁浮列車的激勵頻率。為此，本文從磁浮列車 - 橋耦合振動出發，自編程序對EMS(Electromagnetic Suspension)型高速磁浮列車駛過多跨簡支梁橋過程中多跨簡支梁橋梁的激勵頻率及車體和懸浮架的自振頻率和共振速度進行詳細分析。

1 磁浮列車 - 橋耦合振動模型及動力方程

EMS型磁浮列車是依靠固定在懸浮架上的電磁鐵與軌道上永磁體之間產生吸力而懸浮車體，分為中低速磁浮列車和和高速磁浮列車。以德國高速磁浮列車TR06系列為研究對象，單節列車可簡化成一個車體和四個懸浮架(圖1)。車體與懸浮架通過彈簧阻尼器連接，懸浮架與橋梁之間的電磁力簡化成4個集中力，能夠滿足文獻[12]中規定的均布電磁力數量假定的精度要求。

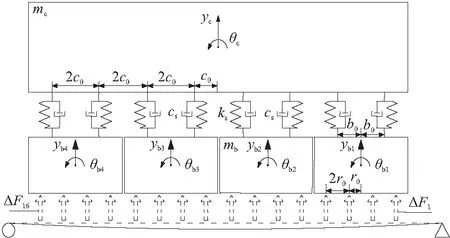
圖1 高速磁浮列車簡化模型

1.1 電磁力方程

電磁力與電流和氣隙成非線性關系，電磁力的表達式為[9]：

(1)

式中：Fi為第i個電磁力；μ為磁導率；A為間隙處電磁鐵鐵芯的橫截面積；N是電磁鐵線圈的匝數；hi是懸浮架上電磁鐵與軌道之間的氣隙；ii為控制電流，下標i的取值為1～16。

任何非線性都存在一個平衡點，對非線性電磁力在平衡點泰勒級數展開進行線性化處理，考慮一階電流項和氣隙項，即：

Fi=F0+ΔFi

(2)

(3)

(4)

電壓、電流之間的關系式可表示[13]：

(5)

式(2)～(5)中：F0為平衡點處的電磁力；ΔFi為動態電磁力；h0為額定氣隙；i0為額定電流；M為懸浮列車總體質量；g為重力加速度；R為線圈電阻；Δii為動態輸出的電流；Δhi為電磁力所對應的懸浮架與橋梁之間氣隙；ΔUi為控制反饋電壓。

控制電壓ΔUi采用懸浮架加速度、懸浮架速度和氣隙間的相對變化位移反饋，即：

(6)

Δhi=yei-yqi

(7)

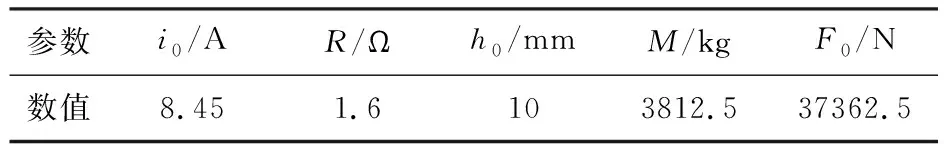
表1 控制系統參數

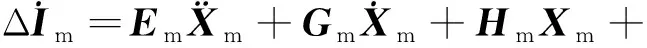
(8)

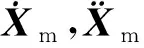
1.2 高速磁浮列車模型及動力方程

假定車體和懸浮架為剛體，每個剛體考慮沉浮和點頭兩個自由度，一個車體和4個剛體共有10個自由度。車輛的位移向量為Xm={yc,θc,yb1,θb1,yb2,θb2,yb3,θb3,yb4,θb4}，單節磁浮列車的動力方程表示如下：

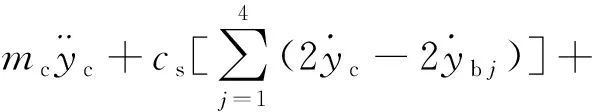
(9)

(10)

(11)

(12)

式中:下標j取值為1～4;mc和mb分別為車體和懸浮架的質量；Ic和Ib分別為車體和懸浮架的轉動慣量；yc和yb j分別為車體和懸浮架的豎向位移；θc和θb j分別為車體和懸浮架的轉角；ks和cs分別對應剛度系數和阻尼系數；c0為彈簧間距的一半；r0為電磁力間距的一半;b0為相鄰電磁力間距的一半。對式(9)～(12)中的元素采用“對號入座”法形成列車的總體動力方程如下：

(13)

式中:Mm，Cm和Km分別為磁浮列車的整體質量矩陣、阻尼矩陣和剛度矩陣；ΔFe為動態電磁力列向量。高速磁懸浮列車主要參數如表2所示[1]。

表2 高速磁懸浮列車參數

1.3 簡支梁橋動力方程

由于磁浮軌道剛度遠小于簡支梁橋的剛度，不考慮磁浮線路軌道的影響，把軌道梁簡化成簡支梁。簡支橋梁的振動運動方程為：

(14)

式中:EI為抗彎剛度；Cv為橋梁阻尼；mv為橋梁線密度；Fe為作用在橋梁上的電磁力；yq為橋梁豎向位移。

式(14)可通過陣型疊加法求解，由于簡支梁高階陣型對橋梁的豎向振動響應影響不大，僅考慮前5階陣型，橋梁豎向位移可表示為：

(15)

(16)

(17)

(18)

(19)

式中:L為簡支梁長度；ξ為橋梁阻尼系數；ωn為橋梁第n階固有頻率；Xn為橋梁位移的廣義坐標；φn為橋梁的第n階陣型。橋梁參數如表3所示[1]。為方便計算，公式(16)的矩陣形式可表示為：

表3 橋梁參數

(20)

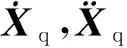
2 磁懸浮列車 - 橋耦合計算程序

懸浮列車 - 橋耦合計算程序主要分為列車、橋懸浮控制系統和橋梁3個子系統，懸浮控制系統產生的電磁力同時作用在列車和橋梁上。3個子系統對應的動力方程分別見公式(8)，(13)，(20)，采用顯式的四階龍格 - 庫塔方法進行求解，無需任何迭代。自編計算程序的基本流程如圖2。程序計算過程中，率先在數據文件中輸入計算步長、行車速度、反饋控制參數等基本參數，再將已經準備好的橋梁質量矩陣、剛度矩陣和阻尼矩陣導入計算主程序。然后采用龍格庫塔方法對動力方程(車輛結構動力方程、控制電流方程和橋梁動力方程)進行求解，得到當前時間步的車輛、電流和橋梁的動力響應，并作為下一時間步的初始條件，依次計算直至計算時間完成。最后導出計算結果并保存。

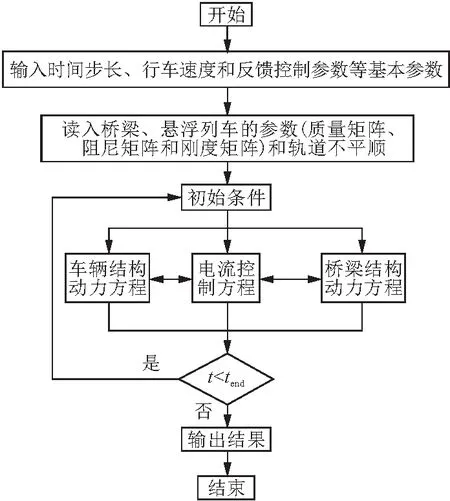
圖2 動力計算流程

3 磁浮列車 - 橋梁耦合計算程序正確性的驗證

高速磁浮列車TR06以速度400 km/h通過多跨長度為24.768 m的簡支梁橋，計算參數如表1，2。不同工況下車體振動穩定后的加速度曲線如圖3所示，簡支梁橋跨中位移曲線如圖4。彈簧和阻尼替代電磁力的車橋耦合振動計算結果與文獻[1]相同，說明程序在此工況中對于計算磁浮列車/橋梁耦合振動的正確性。當選取不同反饋控制參數，車體和橋梁振動響應結果能與彈簧阻尼代替電磁力的車橋耦合振動結果相近。

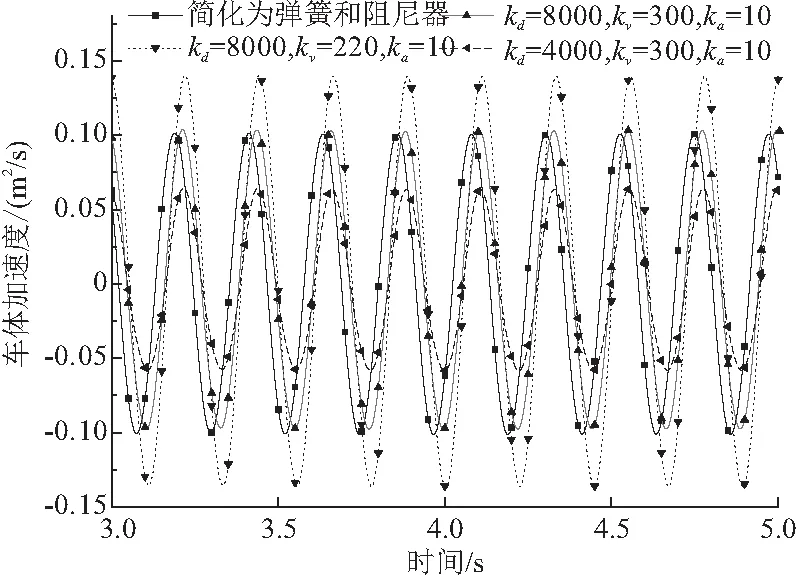
圖3 車體振動穩定后的加速度隨時間的變化曲線

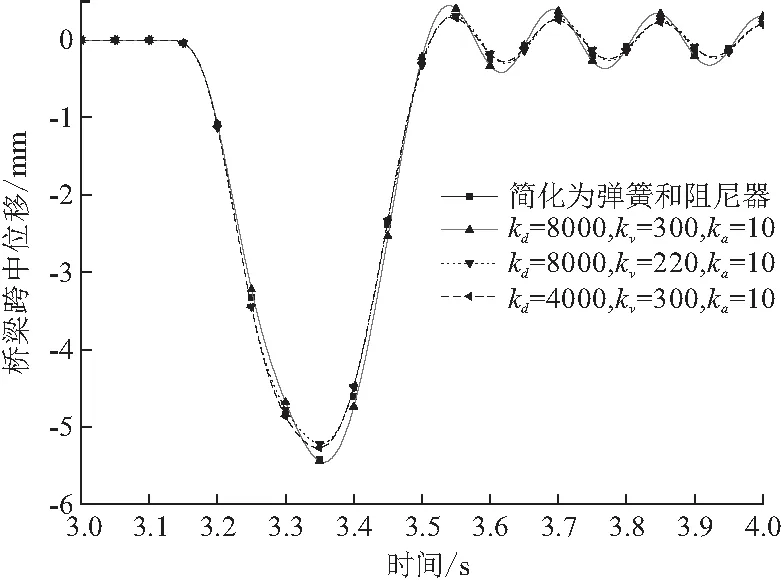
圖4 橋梁跨中位移隨時間的變化曲線

4 高速懸浮列車 - 橋梁耦合振動中磁浮列車共振分析

4.1 磁浮列車振動響應頻率分析

高速磁浮列車TR06以100 km/h的速度通過連續多座長度為24.768 m簡支梁橋，車體和懸浮架豎向振動如圖5所示，頻譜分析如圖6(圖中D為車輛行駛距離)。懸浮架1和懸浮架4的振動幅值以及懸浮架2和懸浮架3的振動幅值都相差不大，其中車體和懸浮架振動響應穩定后做頻率相同的簡諧振動。圖6為了使振幅顯示清楚，橫坐標頻率僅到3 Hz，3 Hz內存在兩個主頻，分別是1.12,2.24 Hz，2.24 Hz對應的振幅遠比1.12 Hz小。磁浮列車 - 橋豎向耦合振動過程中，車輛、橋梁和控制力三者之間相互關聯、相互影響，橋梁和懸浮架動力響應時刻的改變促使氣隙發生變化，從而改變電磁力的大小，進而影響橋梁和懸浮列車的振動狀態。在車輛、橋梁和電磁力這三者相互變化過程中，互相改變的只是振幅和相位，頻率并沒有變化(圖6)。

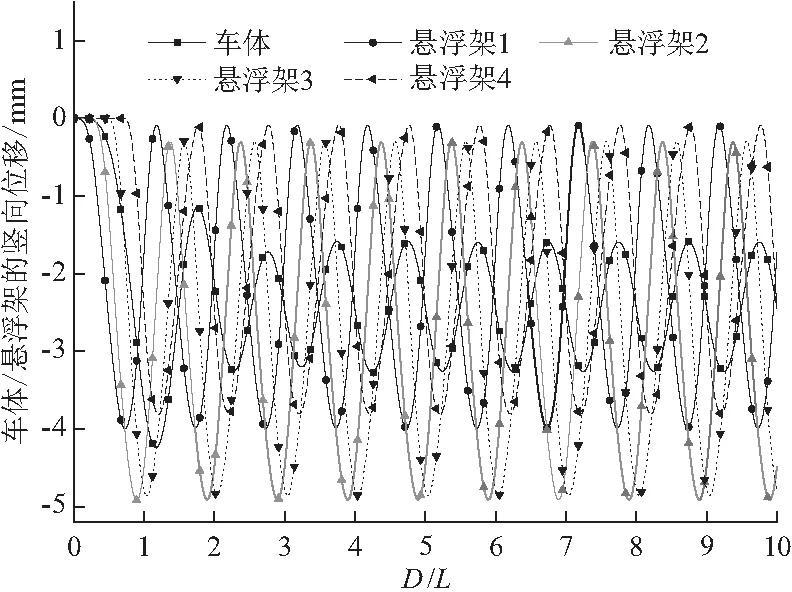
圖5 懸浮列車經過不同橋梁時的動力響應

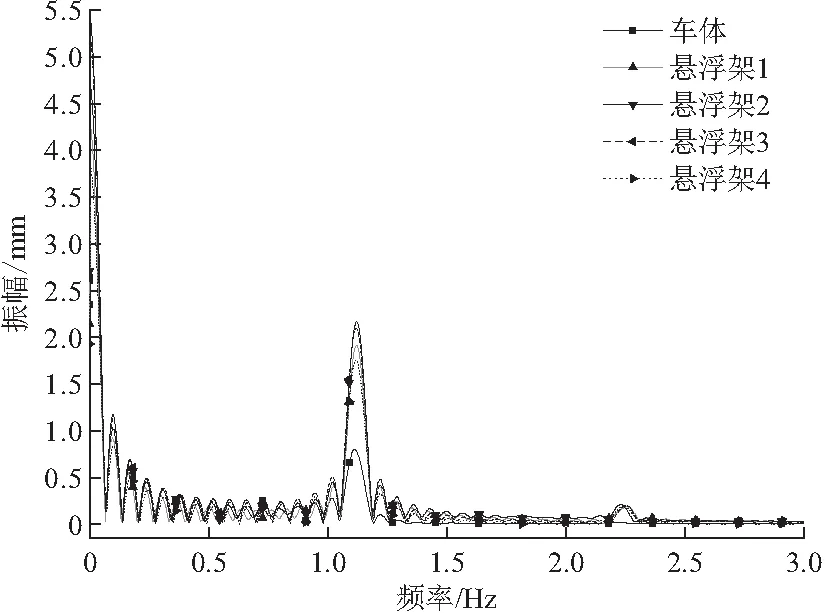
圖6 懸浮列車振幅隨頻率的變化曲線

4.2 磁浮列車振動穩定后的響應頻率計算

磁浮列車車體和懸浮架動力響應穩定后的頻率相同，其車體最大振幅對應的頻率隨速度的變化如圖7。圖中散點擬合函數的比例系數為0.011，線性相關度的平方0.9999近似于1，說明車體和懸浮架振動穩定后的頻率與懸浮列車速度完全成正比。3.6倍于簡支梁橋長度24.768 m的倒數為0.0112，這與正比例系數0.011十分接近了。因此，車體和懸浮架的穩定后的振動頻率數學表達式為：

圖7 車體振動穩定后的響應頻率隨車速的變化曲線

(21)

式中：v為列車行駛速度；L為簡支梁橋長度；f為橋梁對懸浮列車的激勵頻率。由于磁浮列車懸浮架與橋梁之間的氣隙總是趨向于額定氣隙10 mm，因而懸浮架下電磁力對應橋梁位置的橋梁豎向位移影響著懸浮列車的動力響應，磁浮列車跟隨著橋梁上下振動。當列車以速度v駛過多座長度為L的相同橋梁時，電磁力對應橋梁位置的橋梁豎向振動周期為3.6L/v，進而導致磁浮列車車體和懸浮架響應穩定后的振動頻率為f。因此，磁懸浮車橋耦合振動過程中，列車所受橋梁動力響應的激勵頻率為f。此結論與文獻[15]中提出的車橋耦合共振理論完全相符，這也說明磁浮車 - 橋振動中也存在共振現象。

4.3 懸浮列車自振頻率和共振速度分析

不考慮橋梁的影響，懸浮列車在位移脈沖激勵下的動態響應頻譜分析如圖8，其中脈沖激勵函數的高度為1 m，寬度為10-6s。由于脈沖激勵時間足夠短，列車車體和懸浮架做衰減的自由振動，可得到車體的自振頻率為0.72 Hz，4個懸浮架的自振頻率都為3.95 Hz。由式(22)，(23)計算可得車體的共振速度為63.8 km/h，懸浮架的共振速度為352.2 km/h。

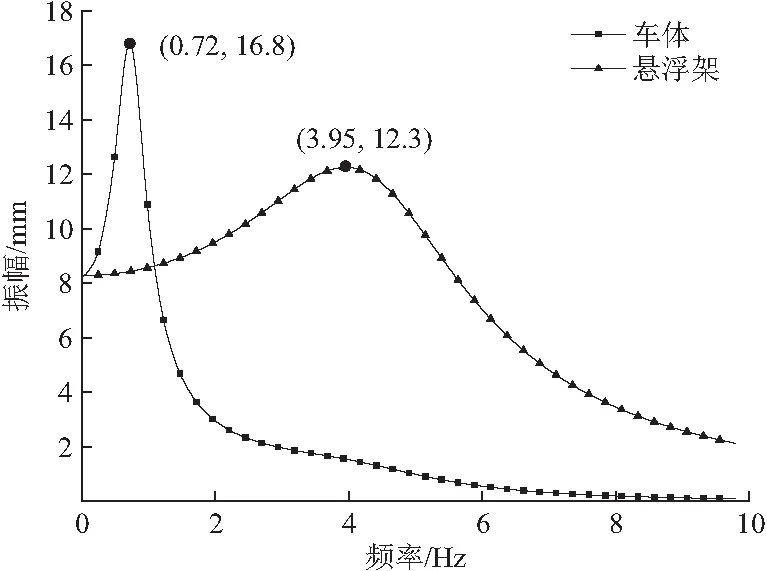
圖8 脈沖激勵下懸浮列車振幅隨頻率的變化曲線

vc=3.6Lfc=63.8 km/h

(22)

vb=3.6Lfb=352.2 km/h

(23)

式中:vc，vb分別為懸浮列車車體和懸浮架的共振速度；fc，fb分別為懸浮列車車體和懸浮架的自振頻率。

4.4 懸浮列車共振速度正確性的驗證

懸浮列車車體和懸浮架振動穩定后振幅隨速度變化曲線如圖9。車體的動力響應普遍比懸浮架小，車體與懸浮架之間的彈簧阻尼能做到很好的減振，以保證乘客的舒適性。車體和懸浮架的振幅先增大后減少，達到最大值的速度不一致，車體在速度為63.8 km/h時振幅最大，懸浮架在速度為352.2 km/h時振幅最大，這與通過車體自振頻率求解的共振速度相符合，說明通過公式(19)轉換求解共振速度的正確性。高速磁浮列車在低速行駛時應盡量避開車體的共振速度63.8 km/h，高速行駛時應盡量避開懸浮架的共振速度352.2 km/h。

圖9 懸浮列車振動穩定后的響應幅值隨速度的變化曲線

5 結 論

通過自編程序，本文建立了磁浮列車 - 橋梁耦合振動模型，在此基礎上分析了橋梁對磁浮列車產生的激勵頻率。通過本文研究可得到如下結論：

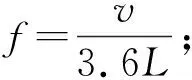
(2)采用脈沖函數作為磁浮列車和控制力的外界激勵輸入，數值模擬求解了磁浮列車車體和懸浮架的自振頻率，其中車體的自振頻率為0.7155 Hz，懸浮架的自振頻率都為3.95 Hz。

(3)利用頻率與行車速度和橋梁長度的關系式換算出懸浮列車車體和懸浮架的共振速度分別為63.8，352.2 km/h，懸浮列車車體和懸浮架振動穩定后的振幅隨行車速度增大先增大后減少，其振幅的最大值都在共振速度處。