兩相混合式步進電動機恒流細分驅(qū)動控制仿真研究

戚振亞，秦倩倩，王立英，呂 強

(中國電子科技集團公司第二十一研究所，上海 200233)

0 引 言

隨著數(shù)字控制技術(shù)的發(fā)展，兩相混合式步進電機的恒流細分驅(qū)動控制技術(shù)在航天步進電機上得到越來越多的應(yīng)用。恒流細分驅(qū)動不但可以使步進電機有更小的步距角、更高的定位精度，而且可以減小電機的振動與噪聲，使電機運行更加平穩(wěn)[1]。

本文從電機轉(zhuǎn)速和電磁轉(zhuǎn)矩角度出發(fā)，建立了混合式步進電動機恒流細分控制Simulink仿真模型，重點仿真分析了在不同細分狀態(tài)下轉(zhuǎn)速和電磁轉(zhuǎn)矩幅值的變化情況，驗證了恒流細分驅(qū)動可以增加電機的運行平穩(wěn)性。

1 兩相混合式步進電動機恒流細分數(shù)學(xué)模型

1.1 混合式步進電動機數(shù)學(xué)模型

MATLAB/Simulink仿真軟件平臺提供了基于SimpowerSystem仿真引擎的混合式步進電機模型[2]。該電機模型主要包括電氣和機械兩部分，其中電氣部分根據(jù)混合式步進電動機電壓平衡方程搭建，機械部分由慣性轉(zhuǎn)矩、粘滯阻尼系數(shù)引起的阻力矩和負載轉(zhuǎn)矩組成的方程搭建，兩部分通過電磁轉(zhuǎn)矩結(jié)合起來，該數(shù)學(xué)模型假設(shè)磁路不飽和，忽略了互感、磁滯效應(yīng)以及各種損耗的影響。

混合式步進電動機相電壓平衡方程[3]：

Vi(t)=RIi(t)+d(LiiIi(t)+LijIi(t))/dt

(1)

式中：Vi(t)為相電壓；Ii(t)為相電流；R為相電阻；Lii和Lij分別為自感和相間互感，二者與轉(zhuǎn)子機械位置角θm有關(guān)。

忽略互感的影響，兩相混合式步進電機相電壓平衡方程：

(2)

由式(2)可見，相電壓由三部分組成，第一部分是相電阻引起的電勢，第二部分是相電流變化引起的感應(yīng)電勢，第三部分是轉(zhuǎn)子位置變化引起的反電動勢。

兩相混合式步進電動機反電動勢可近似表達為：

(3)

式中:Nr為轉(zhuǎn)子齒數(shù);Φm為最大磁通。

兩相混合式步進電機的電磁轉(zhuǎn)矩Te表達式：

Te=-NrΦm[Ia(t)sin(Nrθm)+Ib(t)cos(Nrθm)]-

Tdmsin(2Nrθm)

(4)

式中：Tdm為自定位轉(zhuǎn)矩。

兩相混合式步進電機的機械方程：

(5)

式中:J0為轉(zhuǎn)子轉(zhuǎn)動慣量;B0為粘滯阻尼系數(shù);TL為負載轉(zhuǎn)矩;ωr為機械角速度。

1.2 恒流細分驅(qū)動數(shù)學(xué)模型

恒流細分驅(qū)動實際上是將通入步進電機繞組中的電流由矩形波變成階梯波，使步進電機內(nèi)部合成角度均勻分布的圓形旋轉(zhuǎn)磁場。以四細分為例，四細分是把每個控制周期(360°電角度)均分為16個不同的通電狀態(tài)，每個狀態(tài)相差22.5°電角度(對應(yīng)機械角度0.45°)，如圖1所示，16個不同的通電狀態(tài)下對應(yīng)的兩相相電流波形如圖2所示。

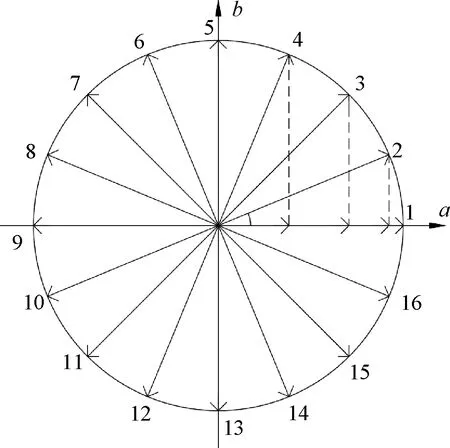
圖1 四細分單個控制周期合成磁場情況

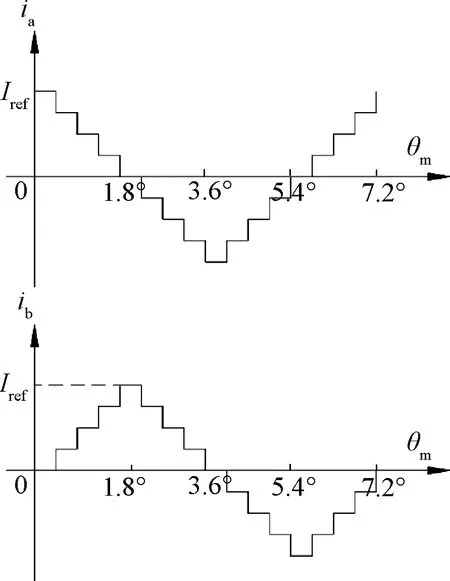
圖2 四細分兩相電機相電流情況

混合式步進電動機等步進角均勻細分控制時，相電流公式[4-5]為：

(6)

式中：Im為電機的額定相電流；α為電流實時電角度；N為細分數(shù)；S為運行步數(shù)。

2 仿真模型的建立

2.1 步進電機仿真模型

本文選用MATLAB/simulink 軟件中自帶的混合式步進電動機仿真模型，該模型正是根據(jù)前文的數(shù)學(xué)模型搭建起來的，如圖3所示，模型主要包括Mechanical、Windings和FEM三個子模塊，Windings和FEM是電氣部分，Mechanical是機械部分，兩部分通過電磁轉(zhuǎn)矩連接起來。

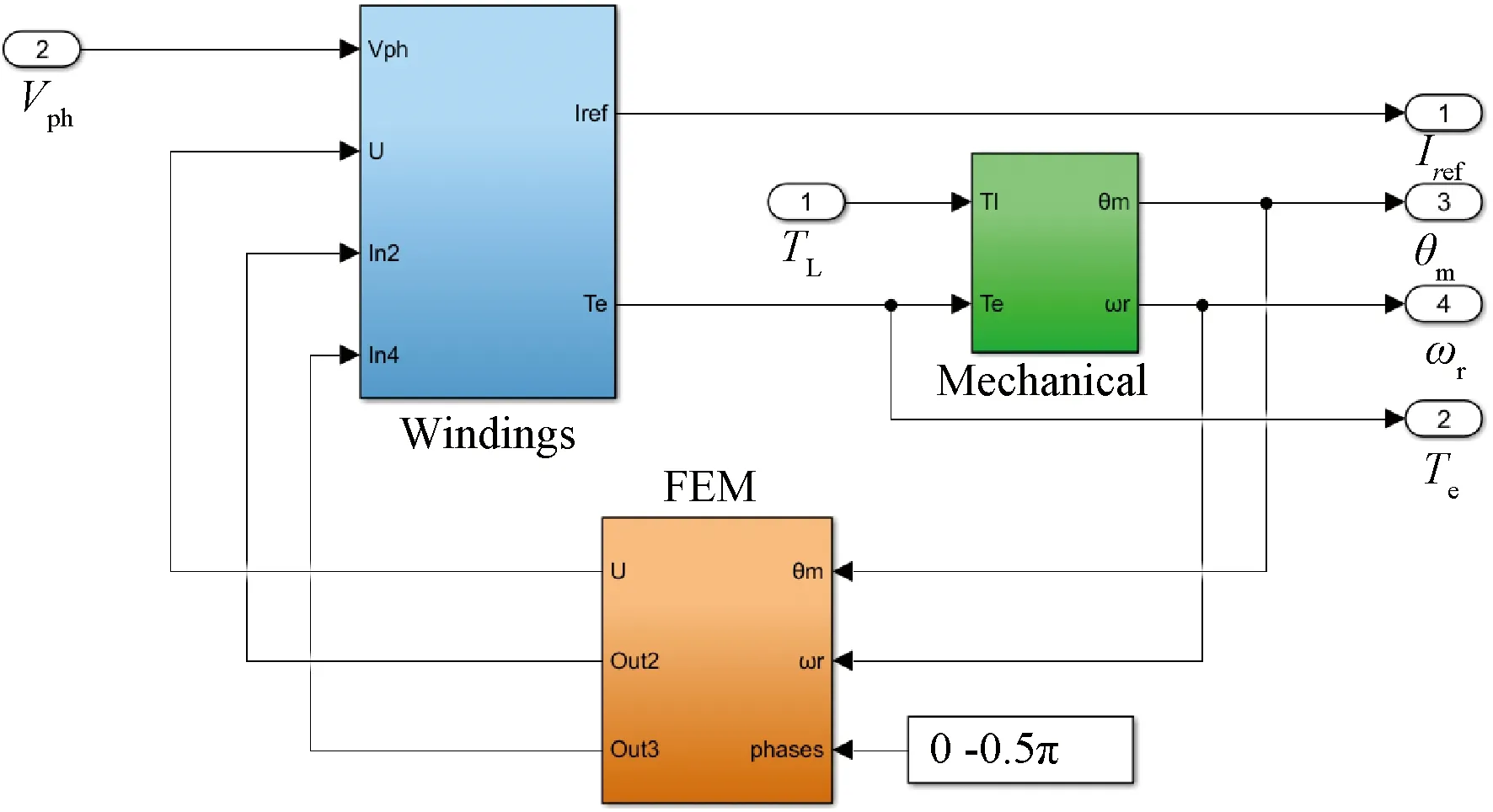
圖3 兩相混合式步進電動機模型

Mechanical子模塊如圖4所示，主要有負載轉(zhuǎn)矩TL和電磁轉(zhuǎn)矩Te兩個輸入端口，轉(zhuǎn)子機械位置角θm和機械角速度ωr兩個輸出端口。

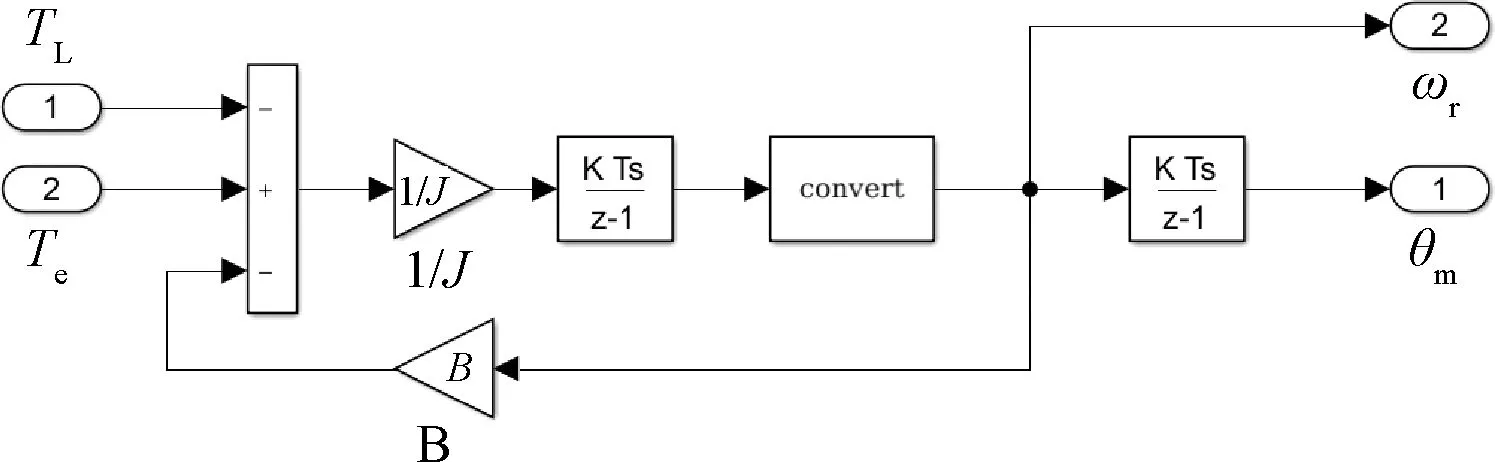
圖4 Mechanical子模塊

Windings子模塊如圖5所示，主要有相電壓Vph、反電動勢U等輸入端口，相電流Iref、電磁轉(zhuǎn)矩Te兩個輸出端口。FEM模型如圖6所示，主要有轉(zhuǎn)子機械位置角θm、機械角速度ωr等輸入端口，反電勢U(V)等輸出端口。

圖5 Windings子模塊

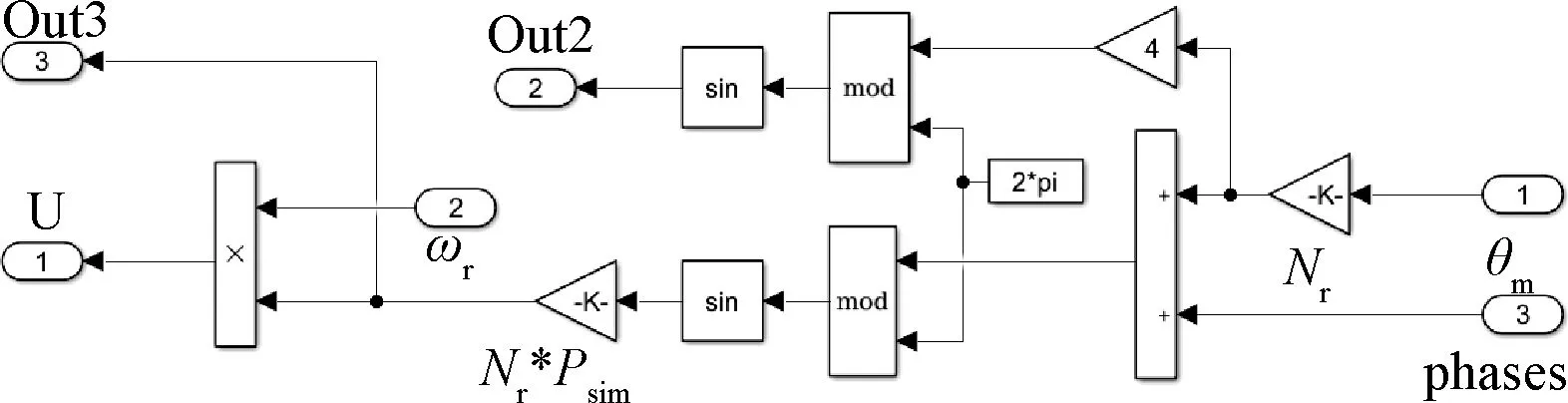
圖6 FEM子模塊

2.2 恒流細分驅(qū)動仿真模型

恒流細分驅(qū)動仿真模型如圖7所示，包括電流細分子模塊、PWM子模塊和功率驅(qū)動模塊三部分。

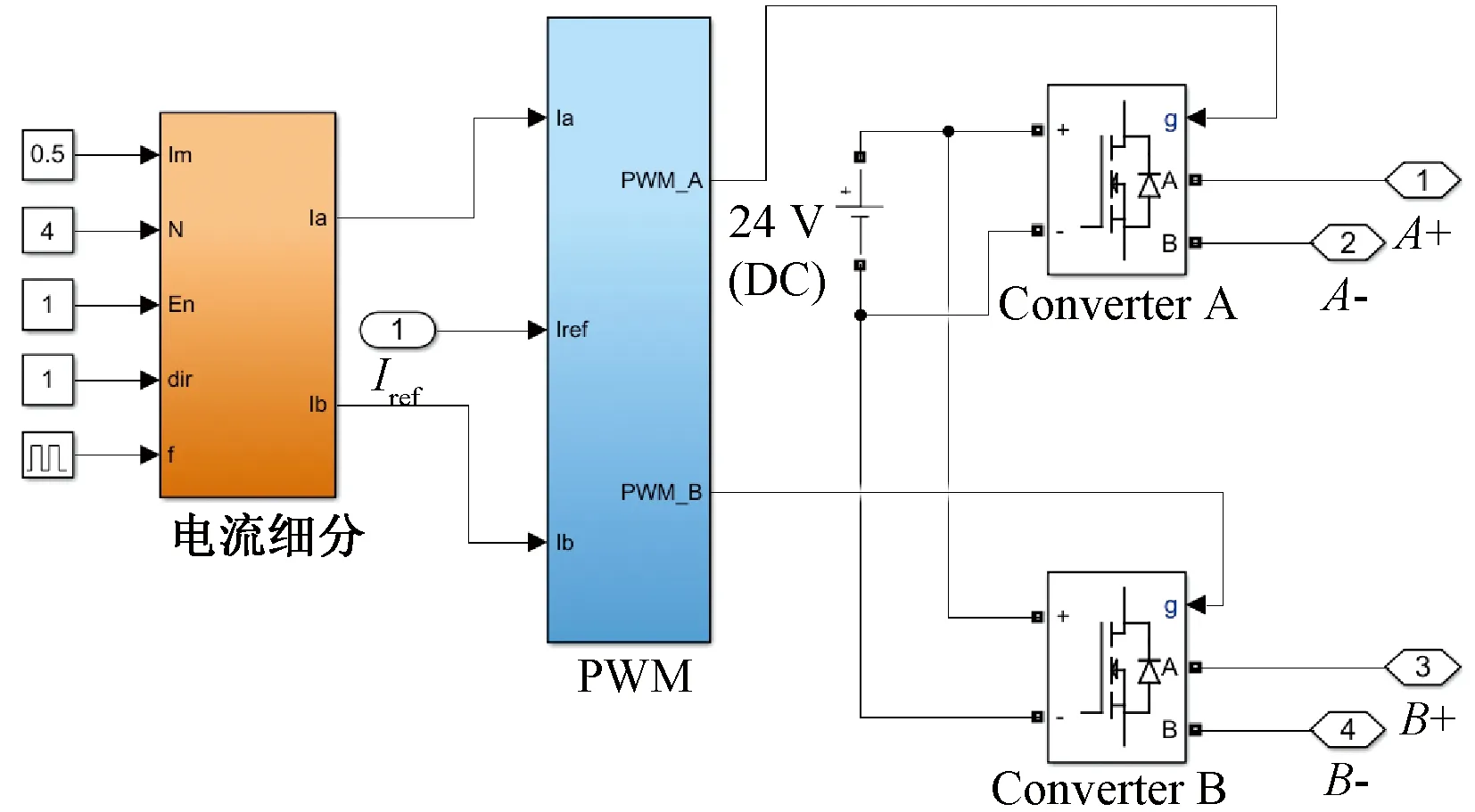
圖7 恒流細分驅(qū)動模型

根據(jù)式(6)的恒流細分數(shù)學(xué)模型，搭建了仿真模型，如圖8所示，主要有步數(shù)S、細分數(shù)N、額定相電流Im等輸入端口，擬合的細分階梯波ia、ib作為輸出端口。

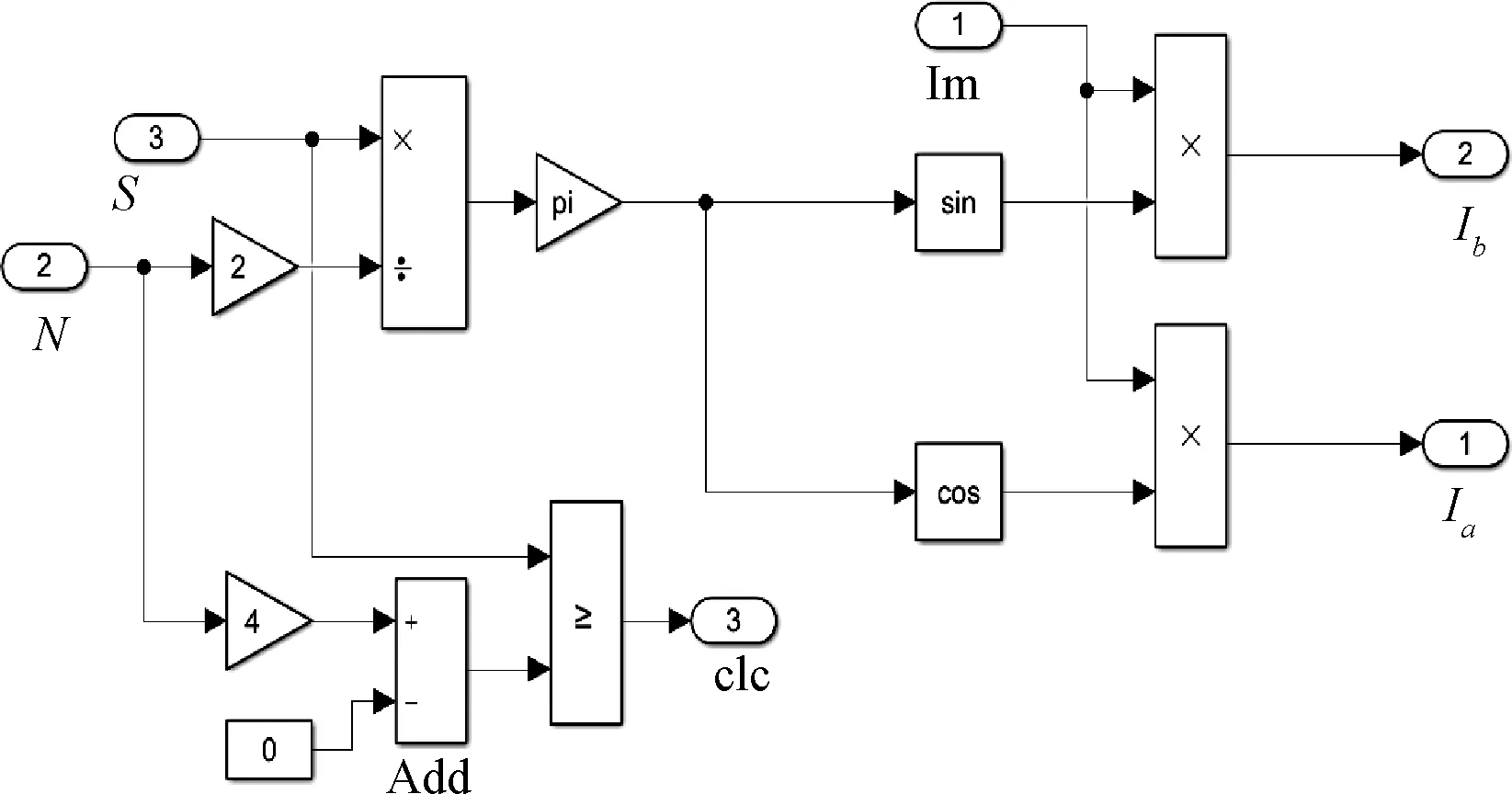
圖8 電流細分模型

PWM模型如圖9所示，擬合的細分階梯波ia、ib與繞組相電流Iref進行比較，通過電流滯環(huán)產(chǎn)生PWM信號，而PWM信號通過控制驅(qū)動芯片的開通和關(guān)斷，進而控制電機轉(zhuǎn)動。

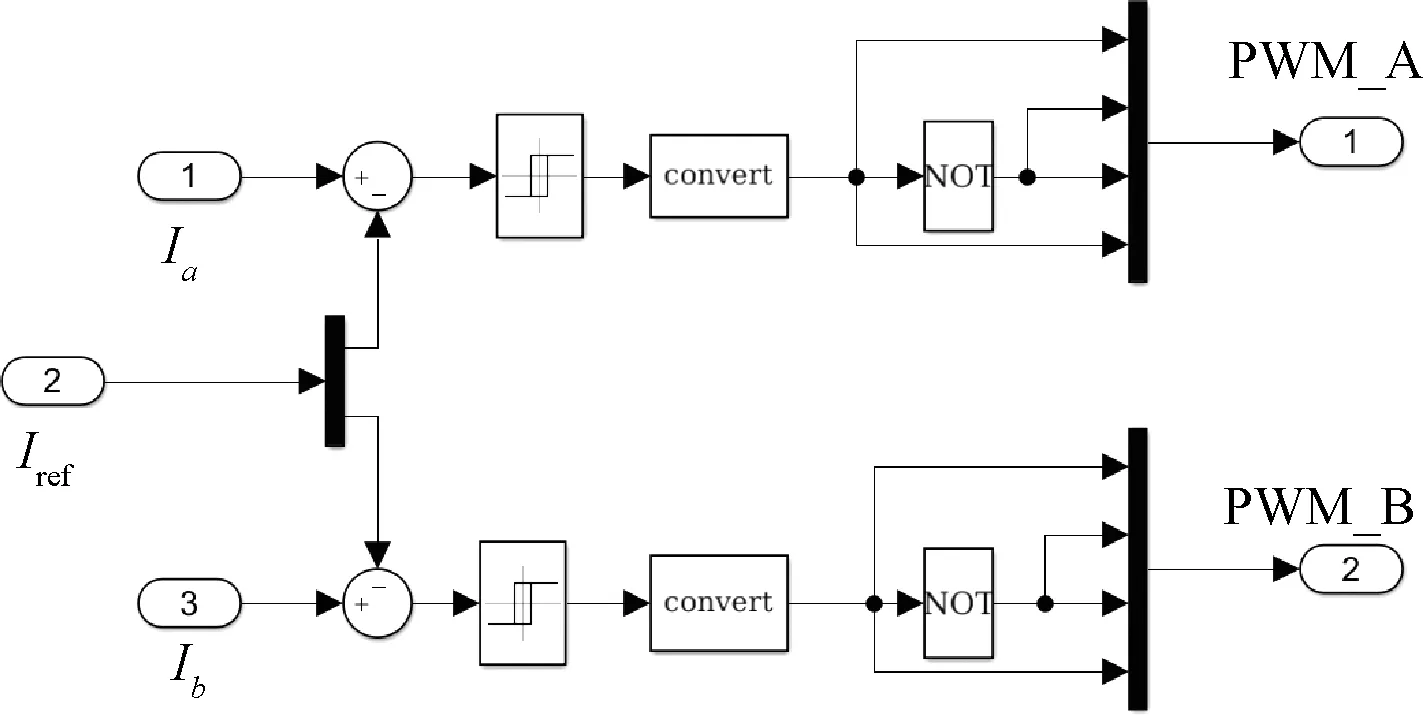
圖9 PWM模型

3 仿真結(jié)果與分析

3.1 電機仿真參數(shù)

仿真電機選用外徑28 mm的混合式步進電動機，電機詳細參數(shù)如表1所示。

表1 電機主要參數(shù)

最終得到的仿真模型如圖10所示。

圖10 兩相混合式步進電動機恒流細分驅(qū)動模型

3.2 仿真結(jié)果分析

保持電機額定電壓24 V(DC)、額定相電流0.5 A和轉(zhuǎn)速150 r/min不變，改變電流細分數(shù)，仿真得到電機在整步、二細分、四細分、八細分和十六細分5種情況下的相電流與轉(zhuǎn)速波形，如圖11～圖15所示；相電流與電磁轉(zhuǎn)矩波形，如圖17～圖21所示。

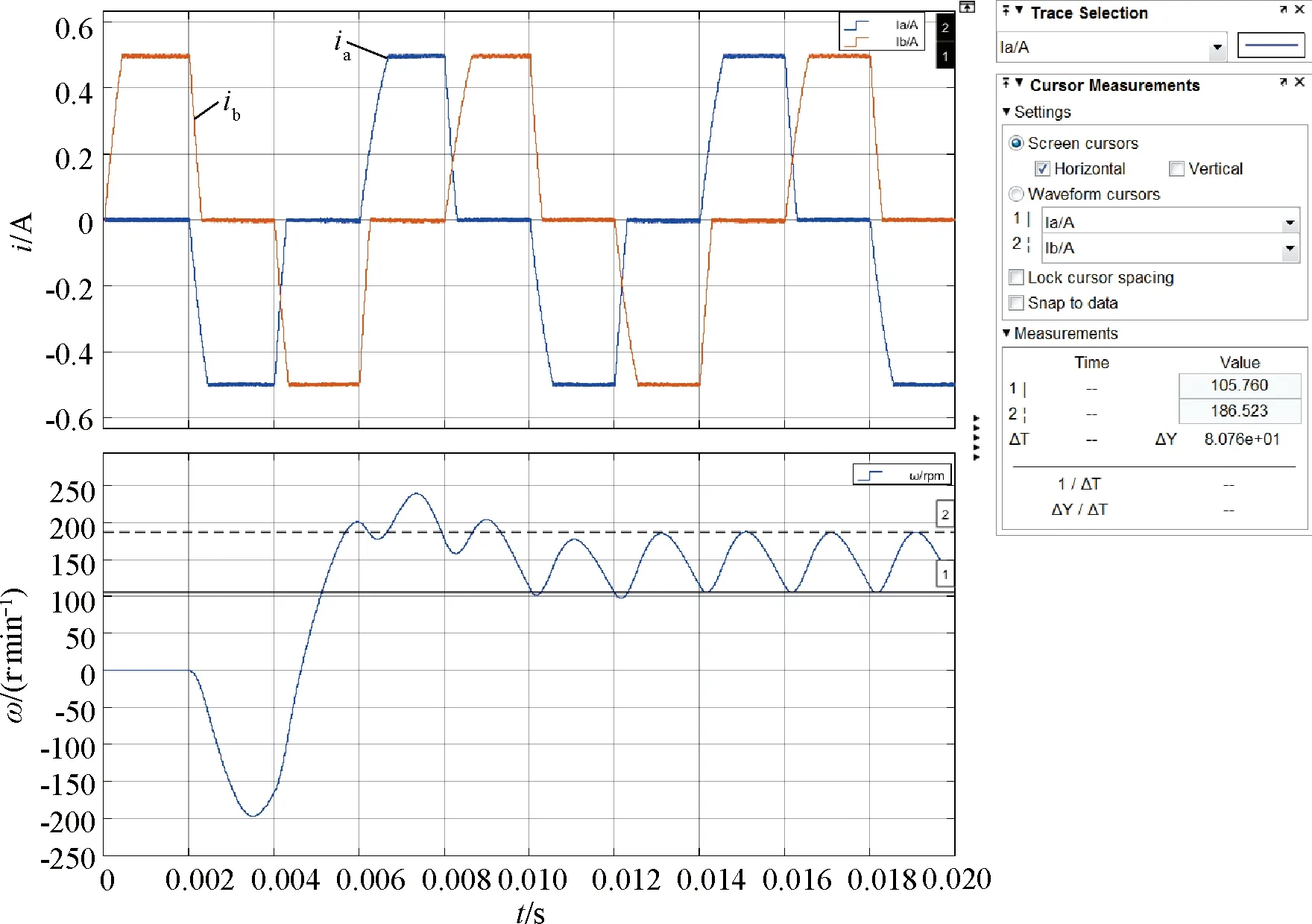
圖11 整步相電流和轉(zhuǎn)速波形

圖12 二細分相電流和轉(zhuǎn)速波形

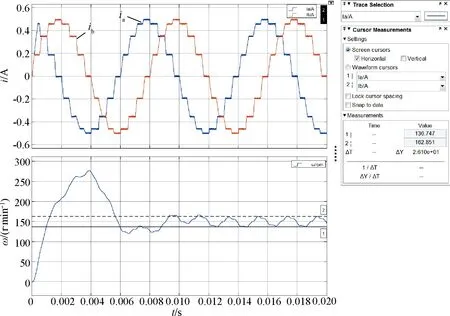
圖13 四細分相電流和轉(zhuǎn)速波形

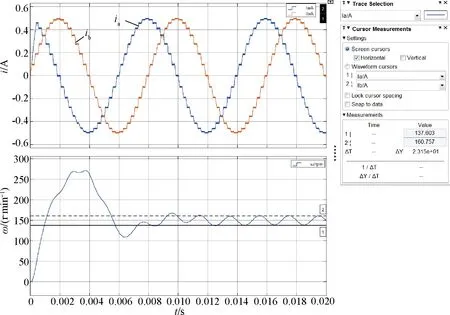
圖14 八細分相電流和轉(zhuǎn)速波形

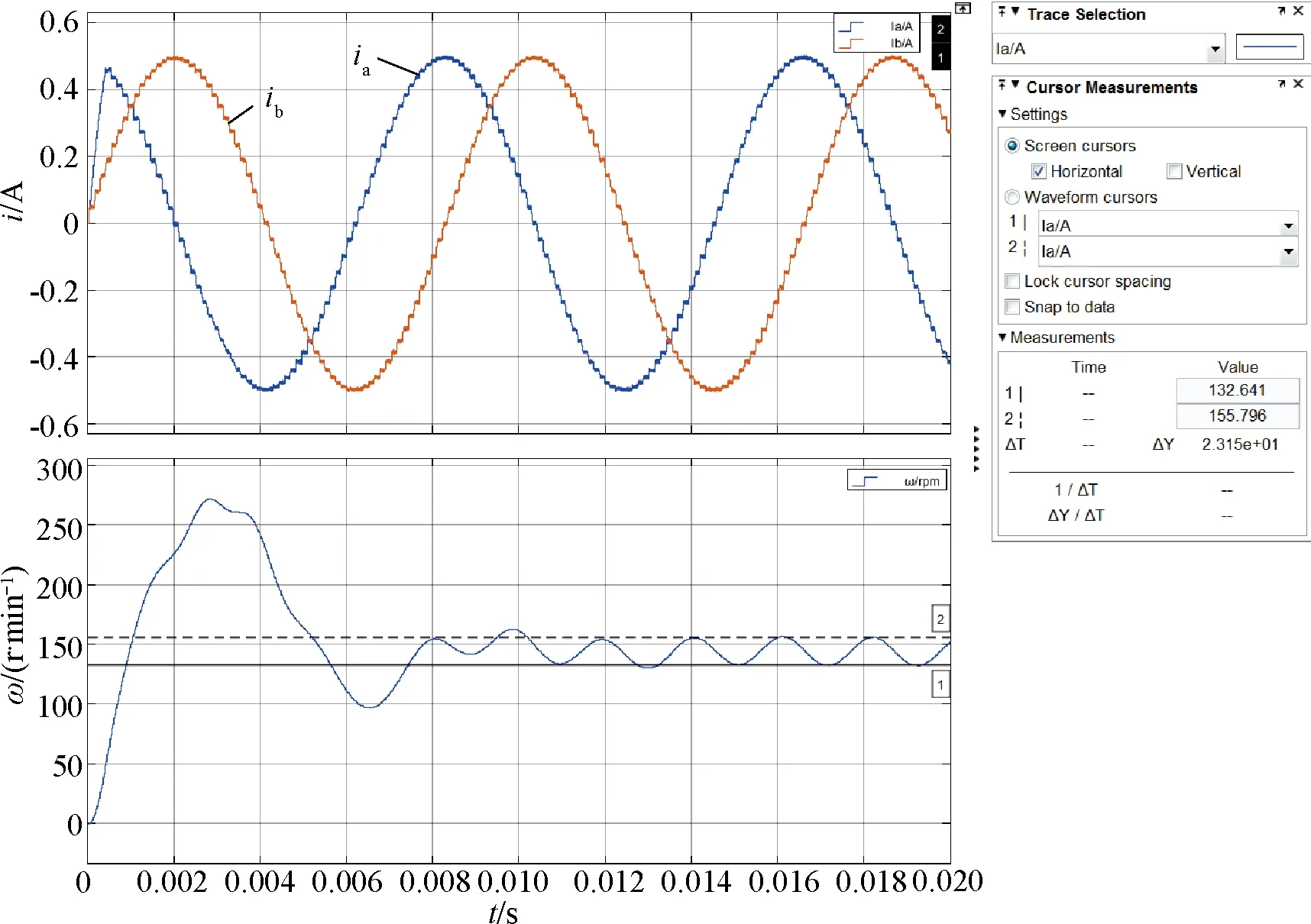
圖15 十六細分相電流和轉(zhuǎn)速波形

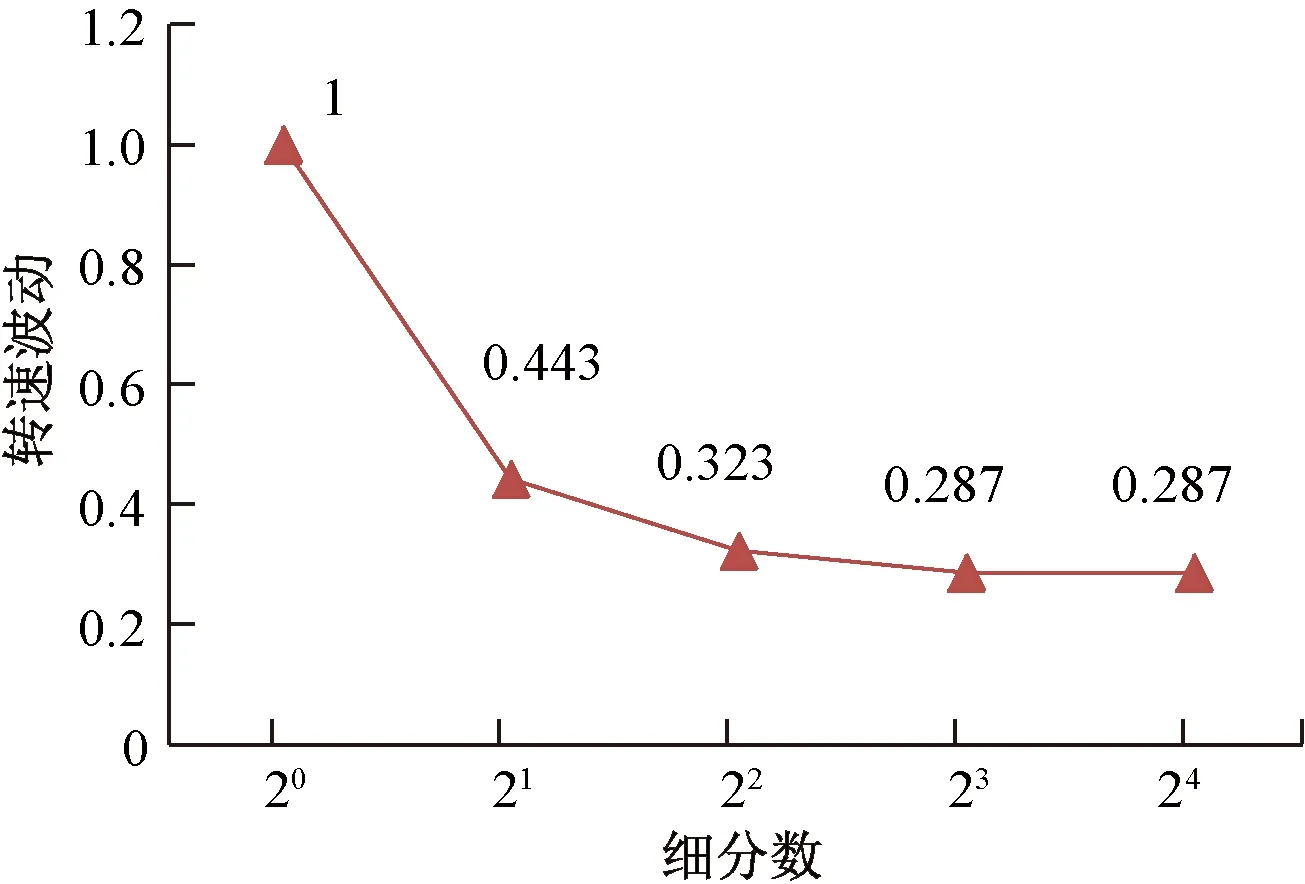
圖16 轉(zhuǎn)速波動與細分數(shù)的關(guān)系

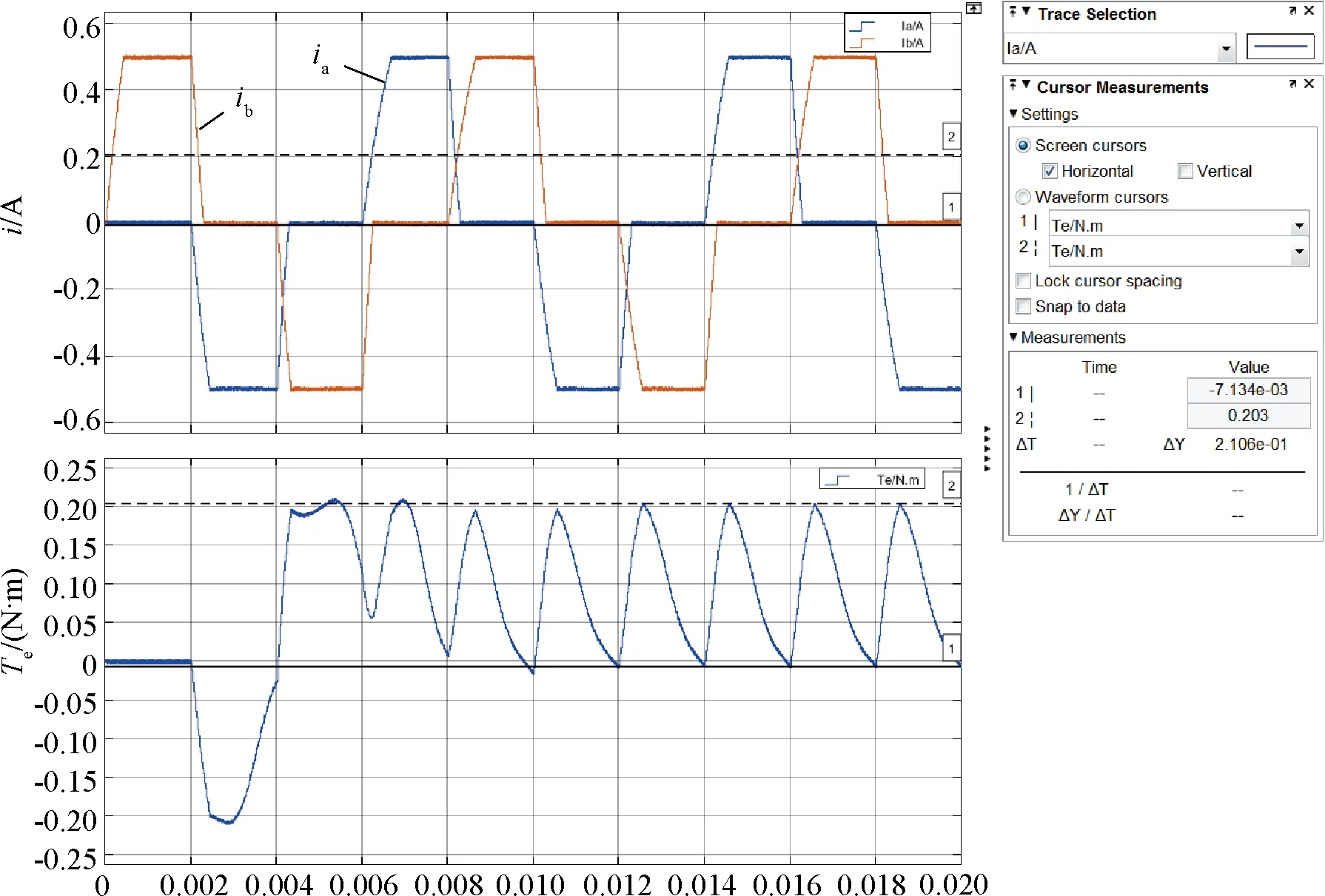
圖17 整步相電流和電磁轉(zhuǎn)矩波形

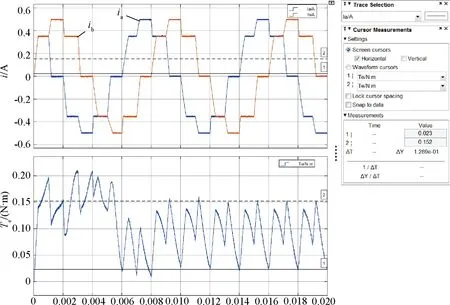
圖18 二細分相電流和電磁轉(zhuǎn)矩波形

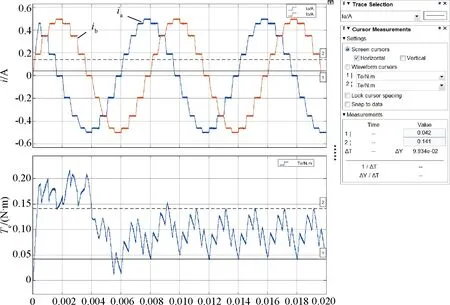
圖19 四細分相電流和電磁轉(zhuǎn)矩波形

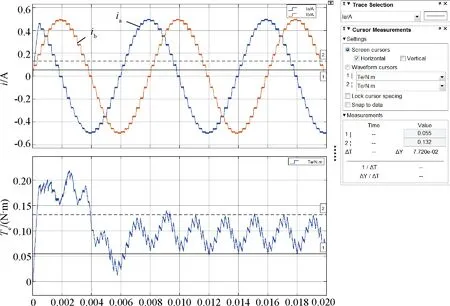
圖20 八細分相電流和電磁轉(zhuǎn)矩波形

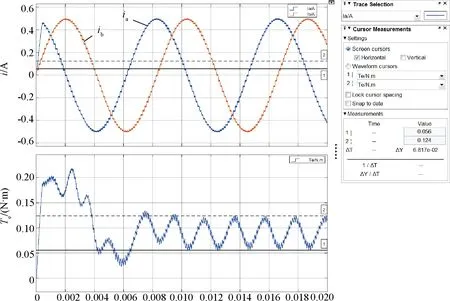
圖21 十六細分相電流和電磁轉(zhuǎn)矩波形

從圖11～圖15中可以看出，在整步、二細分、四細分、八細分和十六細分5種情況下轉(zhuǎn)速峰峰值分別為80.76 r/min、35.82 r/min、26.1 r/min、23.15 r/min和23.15 r/min。仿真結(jié)果顯示，隨著細分數(shù)的增加，轉(zhuǎn)速峰峰值在逐漸減小，如果將整步時電機轉(zhuǎn)速峰峰值作為基準(zhǔn)，那么二細分、四細分、八細分和十六細的轉(zhuǎn)速峰峰值分別為整步時的44.3%、32.3%、28.7%和28.7%，如圖16所示，隨著細分數(shù)的增加，轉(zhuǎn)速波動逐漸降低，細分數(shù)越大轉(zhuǎn)速越平穩(wěn)，二細分時轉(zhuǎn)速波動下降最快，隨著細分數(shù)的增加轉(zhuǎn)速波動趨于穩(wěn)定。

從圖17～圖21中可以看出，在整步、二細分、四細分、八細分和十六細分5種情況下，電磁轉(zhuǎn)矩峰峰值分別為0.2 N·m、0.128 N·m、0.099 N·m、0.077 N·m和0.068 N·m。仿真結(jié)果顯示，隨著細分數(shù)的增加，電磁轉(zhuǎn)矩峰峰值在逐漸減小，如果將整步時電機電磁轉(zhuǎn)矩峰峰值作為基準(zhǔn)，那么二細分、四細分、八細分和十六細分別為整步時的60%、49.5%、38.5%和34%，如圖22所示，隨著細分數(shù)的增加，電磁轉(zhuǎn)矩波動逐漸降低，細分數(shù)越大電磁轉(zhuǎn)矩也越平穩(wěn)，二細分時電磁轉(zhuǎn)矩波動下降最快，隨著細分數(shù)的增加電磁轉(zhuǎn)矩波動趨于穩(wěn)定。

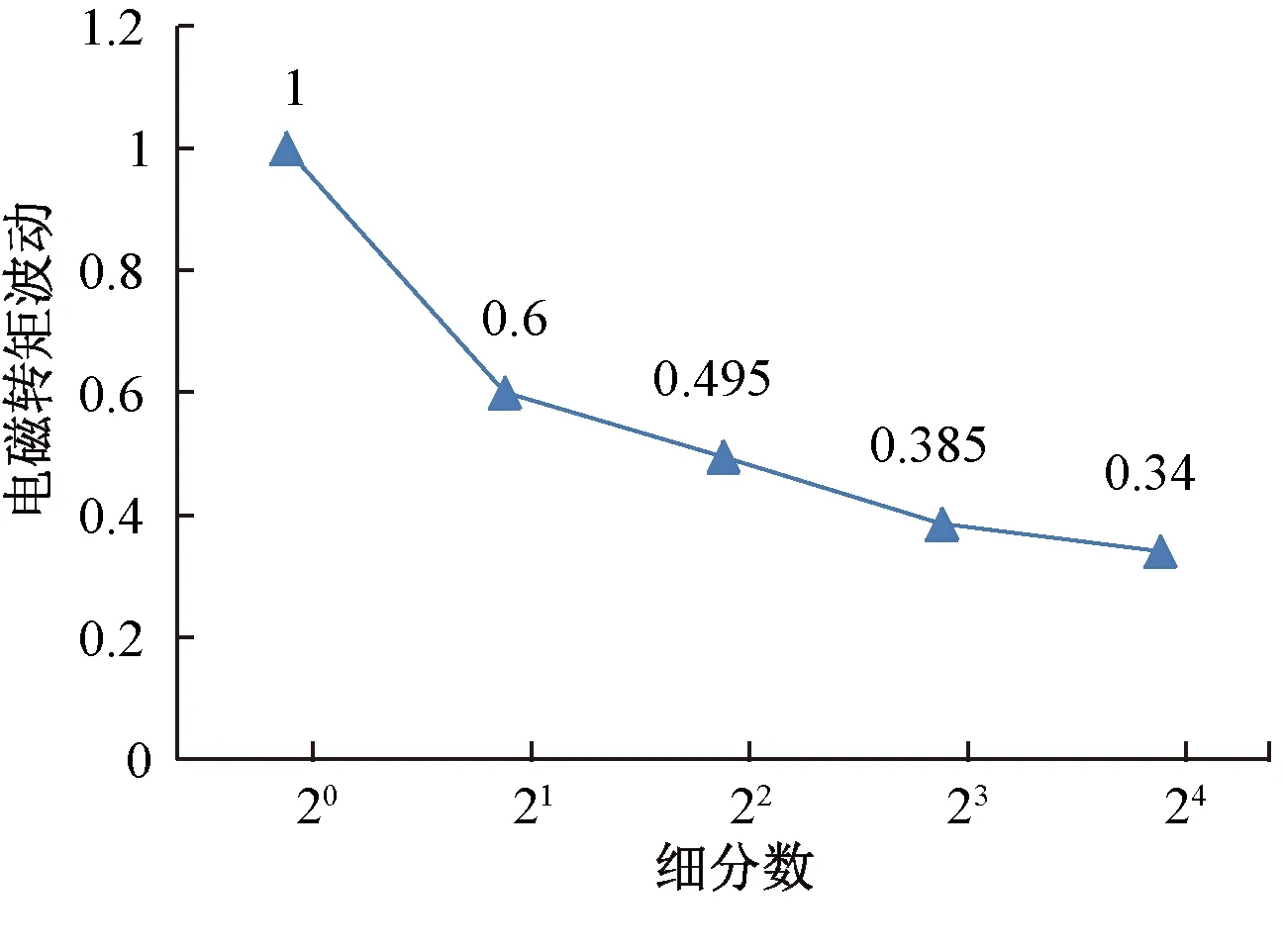
圖22 電磁轉(zhuǎn)矩波動與細分數(shù)的關(guān)系

4 試驗情況

步進電機轉(zhuǎn)矩波動測試不能像其它永磁電機一樣采用堵轉(zhuǎn)等方式進行，并且目前也暫未發(fā)現(xiàn)有更適合的測試方法。而轉(zhuǎn)速波動雖然可以直接測試，但是市場上測試系統(tǒng)的最小采樣間隔為0.1 s，在不同細分情況下測出的平均轉(zhuǎn)速基本相同，偏差為±3 r/min，因此也不具有實際參考意義。

對步進電機來講，細分的不同最終體現(xiàn)在電機的振動和噪聲上，因此本文從細分與電機振動的角度出發(fā)，搭建了步進電機振動測試平臺，如圖23所示。對不同細分下的電機振動情況進行了測試，整步、二細分、四細分、八細分和十六細分情況下電機振動總量分別為45.8 mm/s，38.7 mm/s，34.3 mm/s，30.5 mm/s和28.2 mm/s。從試驗結(jié)果可以看出，隨著細分數(shù)的增加電機振動逐漸減小，電機運行逐漸平穩(wěn)，與仿真結(jié)論一致。

圖23 步進電機振動測試平臺

5 結(jié) 語

本文對兩相混合式步進電動機恒流細分驅(qū)動技術(shù)進行了研究，搭建了基于MATLAB/Simulink的恒流細分驅(qū)動仿真模型，仿真分析了不同細分數(shù)下的轉(zhuǎn)速和電磁轉(zhuǎn)矩，最后搭建了電機振動測試平臺，對步進電機在不同細分下的自身振動情況進行了測試，得出如下結(jié)論：

1)仿真結(jié)果顯示，隨著細分數(shù)的增加，轉(zhuǎn)速波動和電磁轉(zhuǎn)矩波動逐漸減小，即恒流細分驅(qū)動可以有效地降低轉(zhuǎn)速和電磁轉(zhuǎn)矩波動，進而降低電機振動與噪聲，使電機運行更加平穩(wěn)。

2)搭建了步進電機振動測試平臺，對步進電機在不同細分情況下的振動進行了測試，試驗結(jié)果顯示隨著細分數(shù)的增加電機振動逐漸減小，電機運行越平穩(wěn)，與仿真結(jié)論一致。

3)對步進電機轉(zhuǎn)速和轉(zhuǎn)矩波動的測試方法還有待進一步的研究。