時滯反饋下高速磁懸浮軸承轉子系統的穩定性分析

鄭 凱

（1.中國航發沈陽發動機研究所，2.中國航空發動機集團航空發動機動力傳輸重點實驗室：沈陽 110015）

0 引言

磁懸浮軸承具有轉速高、無需潤滑、工作溫度范圍廣、可測可控性好等諸多優點。作為航空多電發動機的重要組成部分，各國研究機構和學者對其高度關注，并在其控制方法、動力學分析和試驗應用等方面開展了大量研究工作。最近的研究發現，一些在機電系統中常被忽略的微小時滯可能對高速運轉的磁懸浮軸承轉子系統的穩定性和動態性能產生很大影響。這些時滯包括位移信號的采集、處理、轉換、控制算法在CPU中的運算等過程所消耗的時間，以及執行單元中功率放大器的飽和效應和電磁鐵線圈中的渦流損耗和磁滯特性所產生的滯后效應等，其量級為幾十微秒，在系統相對簡單、時滯環節不多且對于系統動力行為無嚴格限制的情況下，忽略其產生的效應并無不妥。但考慮到航空發動機等重要設備的高可靠性要求，對于工作在苛刻條件下的復雜機電系統，其設計技術和控制理論研究必須構筑在更加嚴密的體系框架之下，進一步的探索也必須認真考慮時滯的作用。

目前對于磁懸浮軸承時滯問題的研究已經引起了一些關注。Wang等討論了1個含有輸入時滯的單自由度系統的穩定性與Hopf分岔問題，利用中心流形約化和范式方法討論了Hopf分岔的方向及分岔周期解的穩定性；Jiang等在其基礎上著重研究了當系統特征方程有1個零特征根和1對純虛根的情形，給出了完整的穩定性分岔分析；Ji等研究了由PD反饋控制的簡單Jeffcott轉子系統的時滯問題，證明了較小的時滯依然可以影響系統的非線性響應，又將研究擴展到較復雜的2自由度徑向轉子系統。上述研究發現，當時滯超過1個關鍵點時，會發生Hopf分叉，轉子運動由平衡點解轉變為穩定的周期解；而當時滯未達到關鍵點時，其對系統動態性能的影響可以忽略。值得注意的是，以往的研究大多關注于轉子系統靜止或低速轉動下的平衡點解，對其產生影響的時滯數量級可能在毫秒級，對于機電控制系統的時滯一般是在微秒級，如此小的時滯對平衡點解的影響幾乎可以忽略不計。而在實際應用中，電磁軸承所支撐的轉子運轉于高速狀態下，且由于轉子偏心的存在，其運動的固有解為受迫振動的周期解，即使是微秒級時滯，也可能與轉子高速渦動的周期數量級接近，進而可能對轉子系統的動態性能和穩定性產生重大影響。

本文著重分析了微小時滯對于高速轉子受迫振動周期解的影響，利用數值方法討論了轉子系統周期解隨時滯的變化規律以及穩定性切換問題。

1 磁懸浮軸承系統時滯動力學模型

在實際中磁懸浮軸承-轉子系統可以簡化為2自由度剛性轉子系統，如圖1所示，、方向上2對磁極對稱安裝。

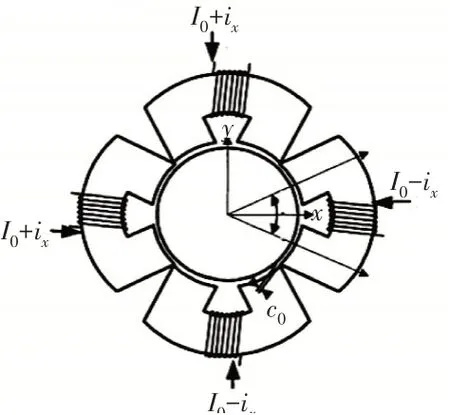
圖1 2自由度電磁軸承-轉子系統

當轉子處于幾何中心時，到電磁鐵的氣隙都為。為了建立磁場，同一自由度上兩側的電磁鐵線圈中通有相等的電流，稱為偏磁電流。以方向為例，當轉子發生偏移，則轉子與左側磁鐵之間的距離為+，與右側電磁鐵之間的氣隙為-。此時控制器輸出的控制電流為，依照差動模式驅動電磁鐵，則兩側磁極中的電流分別為+和-，保證將轉子拉回到平衡位置，在方向上2個磁極產生的電磁力F 為

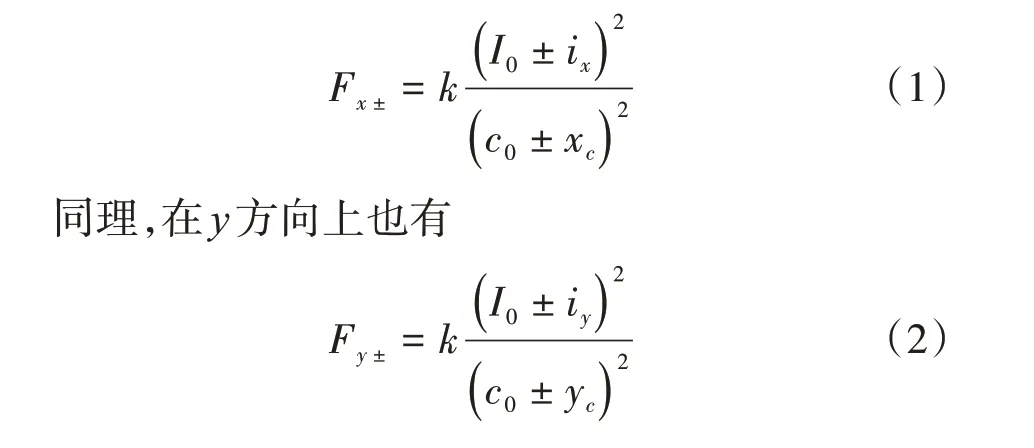
式中：為電磁力常數；、分別為、方向上的位移。

將、方向自由度之間的幾何耦合效應考慮在內，則轉子在、方向上的動態方程分別為

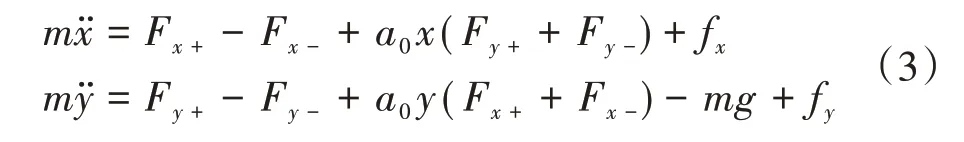
式中：為幾何耦合系數；為轉子質量；f 、f 分別為、方向上的偏心力，=sin（），=cos（）。

若控制器選用PD控制器，假設2個自由度控制回路中的時滯大小皆為，即控制器實際依照時刻的系統狀態來施加控制，則控制電流i和i可表示為

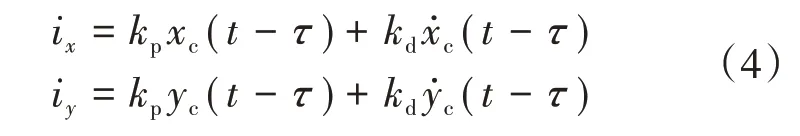
式中：為比例控制系數；為微分控制系數。

由于多尺度法等近似解析方法推導過程冗繁，所能處理問題的維數較小，對于自由度較多且各自由度之間存在耦合的系統分析起來比較困難，因此本文采用厚度為時滯的龐加萊板打靶法，以考慮了極間耦合效應的2自由度剛性轉子系統為研究對象，對其時滯動力學問題進行研究。

2 數值分析方法

本文借助文獻[14]中改進打靶法的思想對磁懸浮軸承系統周期解的時滯問題進行研究，將求解系統周期解的過程轉化為求取“厚度為”的龐加萊板上的不動弧，如圖2所示。

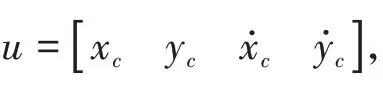
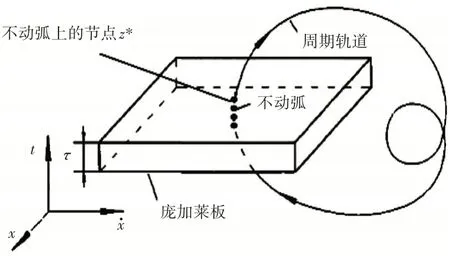
圖2 龐加萊板上的不動弧

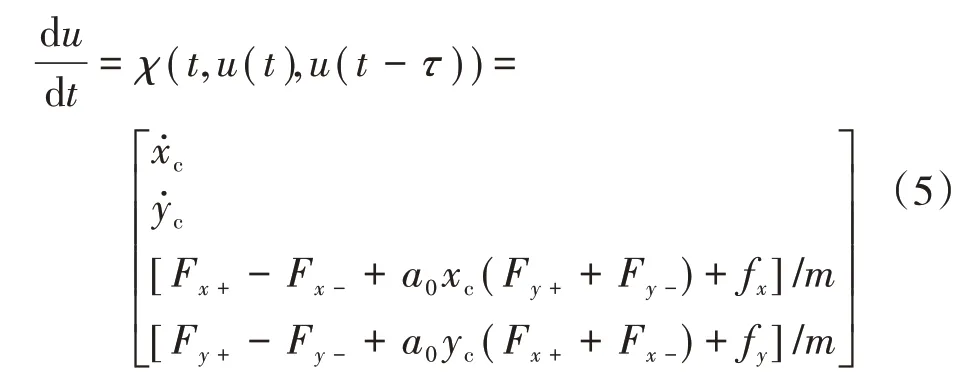
將時間區間[-,]分為-1個等距小區間，系統在時間區間[-,]內的運行弧線上可以分為個節點：

u =(+t ),t =-+(-1)/(-1),=1,2,,，取=[...u ]，定義為龐加萊映射算子，則系統可表示為龐加萊映射的形式

其中（）表示系統以（）為初始值經歷1個龐加萊映射周期后的狀態，而求解系統（5）的周期解可以轉化為求取“厚度為”的龐加萊板上的不動弧，不動弧上的節點滿足*=(*)。

選取龐加萊板初始弧線上節點，對式（6）采用牛頓-拉普森迭代公式有

式中：為新的迭代節點；為單位方陣；()為龐加萊算子在處的雅可比矩陣。

取,分別為(),(-)的偏微分算子，式（7）中((),())可以通過微分方程組

采用數值積分法對1個龐加萊周期求積分獲得，即

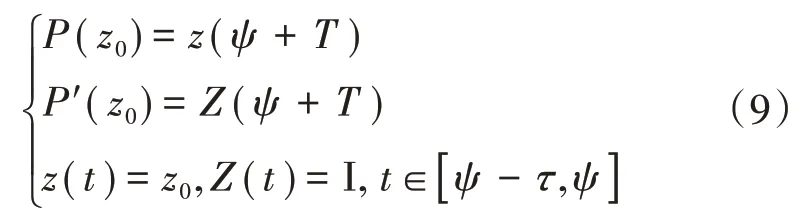
將所求得的(),()代入式（7）計算出新的迭代點，經過反復迭代得到系統的周期解，迭代過程的流程如圖3所示。

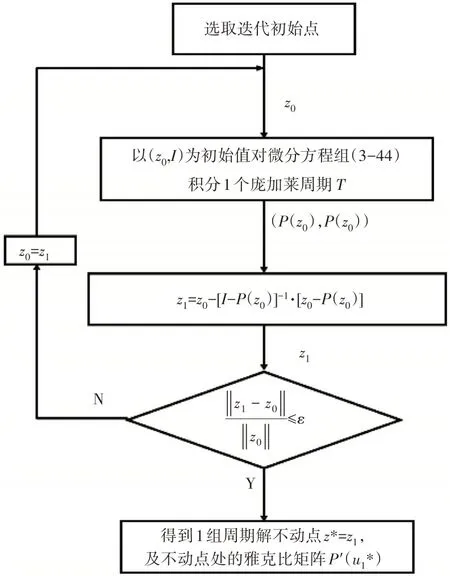
圖3 迭代流程

經過上述迭代過程，最終得到系統的周期解不動弧上的1組節點*，同時求得龐加萊算子在*處的雅可比矩陣(*)。根據Floquet理論，矩陣(u *)的特征值即為所得周期解的Floquet乘子，且有：

（1）若Floquet乘子模的最大值小于1，系統周期解是穩定的；

（2）若Floquet乘子模的最大值大于1，系統周期解是不穩定的；

（3）若Floquet乘子模的最大值等于1，系統周期解處于臨界穩定狀態。

由此對所得周期解的穩定性進行判定。

3 數值分析結果

選取1個實際的電磁軸承剛性轉子系統作為研究對象，系統參數如下。

（1）轉子：質量=9.6 kg，偏心距=0.02 mm。

（2）電磁軸承：=4 A，=0.4 mm，=8.63×10Nm/A，=0.16/。

（3）控制器參數：k =89280A/m，k =5A·s/m。

設定轉子轉速為25000 r/min，利用第2章中所描述的算法在不同時滯下進行計算分析，系統周期解的振幅隨時滯的變化如圖4所示。從圖中可見，隨著時滯的延長，振幅緩慢增大，時滯對于穩定周期解振幅的影響并不明顯。

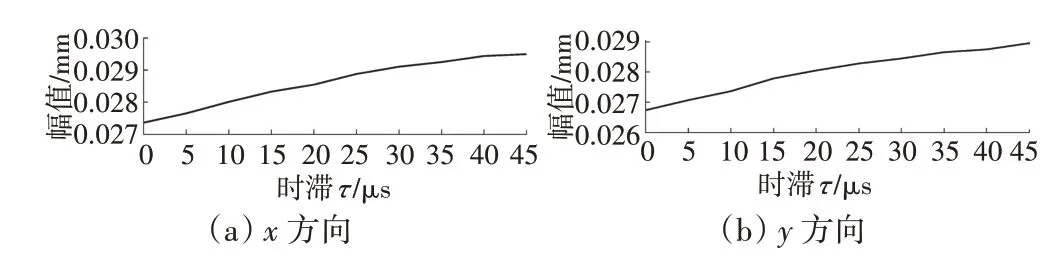
圖4 周期解振幅隨時滯的變化

不同時滯下計算出的模最大的Floquet乘子如圖5所示。從圖中可見，隨著時滯的延長，Floquet乘子逐漸接近單位圓，當時滯達到43μs時，以共軛復數方式穿出單位圓，轉子系統不再具有穩定的周期解。

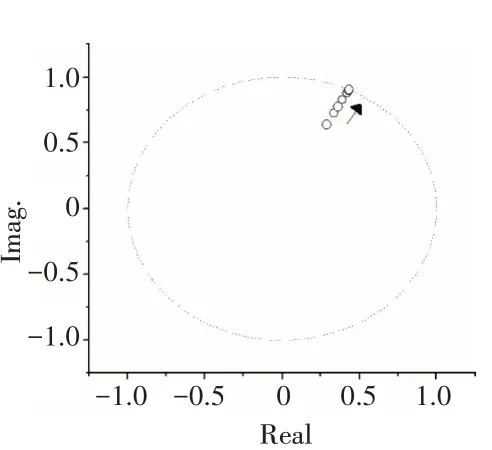
圖5 模最大的Floquet乘子

時滯分別為0、40.0、43.2、44.0μs時轉子的軸心軌跡如圖6所示。從圖中可見，隨著時滯的延長，轉子運動從穩定的周期運動（圖6（a）、（b））轉變為概周期運動（圖6（c）），而當時滯達到44μs時，轉子系統失穩（圖6（d））。

圖6 不同時滯下轉子的軸心軌跡

對于時滯在不同轉速下對轉子系統穩定性的影響的進一步研究發現，在轉速較低的情況下，引起轉子系統失穩的時滯大小都在毫秒級，遠遠高于一般機電控制系統中可能出現的時滯，而當轉速升高至約18000 r/min時，失穩時滯縮短至只有60μs。各轉速下的失穩時滯如圖7所示。從圖中可見，隨轉速升高，能夠使轉子系統周期解失穩的時滯明顯縮短，說明隨轉速的升高，微小時滯對于轉子系統穩定性的影響也更為顯著。當轉速升高到60000 r/min時，轉子系統在時滯約為19μs的情況下就可能失穩（如圖8所示），而如此短的時滯對于采用數字控制器的電磁軸承系統來說是難以避免的。

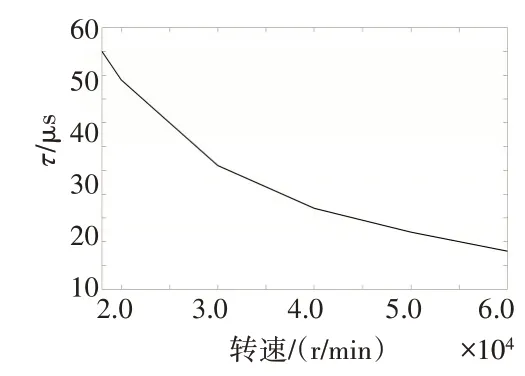
圖7 各轉速下的失穩時滯

圖8 轉子軸心軌跡（ω=60000 r/min、τ=19μs）

4 結束語

本文研究了時滯對于不平衡擾動下磁懸浮軸承轉子周期解的影響，結果表明，對于高速轉子系統，在控制反饋回路中即使存在微秒級的微小時滯，也可能對系統的動態特性和穩定性產生重大影響，使得動態性能降低甚至失穩；并且隨著轉速升高，時滯的影響更為顯著。

因此進行高速轉子系統設計和控制時，需要考慮時滯的影響。目前對類似于電磁軸承等復雜機電系統的時滯問題的研究在國內外均尚處于初級階段，對系統時滯的精確測算以及時滯系統的魯棒控制等問題還有待進一步研究。