克服熱慣性的氣流溫度動態測量方法

鄭 燁, 鄒 靜, 張瑜燦, 王選擇

(1.湖北工業大學 機械工程學院,湖北 武漢 430068； 2.國網湖北省電力有限公司技術培訓中心,湖北 武漢 430040)

0 引 言

測溫傳感元件的熱接點與被測介質進行熱量交換后,自身溫度上升或降低到穩定值需要一定時間,從而使熱接點的溫度變化總滯后于被測介質的溫度變化,這種現象稱之為熱慣性。目前廣泛使用的熱電偶、熱電阻等接觸式溫度傳感器均具有熱慣性[1]。

熱敏電阻是一類由半導體材料制成[2],且電阻率隨溫度發生明顯變化的電阻,相對于熱電偶、鉑熱電阻等溫度傳感元件,熱敏電阻具有體積小、抗輻射、耐振動、靈敏度高、成本低、易于集成、精度較好等優點[3,4],在溫度測量、控制及溫度補償等領域有著廣泛運用[5]。隨著現代科技的高速發展,僅提高熱敏電阻在穩態下的準確度已經無法滿足當今的測量[6]。對于溫度隨時間快速變化,且測量環境常伴有高速氣流流動的一次性過程,溫度傳感器應能迅速感受變化的溫度并實現有效跟蹤。傳統的直接用傳感溫度代替實際溫度的熱敏電阻測溫方法,由于熱慣性特點,難以實現準確的動態快速測量。因此,如何減小接觸式溫度傳感器的熱慣性與改善其熱響應特性以達到動態測溫要求,是實現氣流高速測量的前提,這也是現代測溫的發展方向[7]。

本文分析熱敏電阻測溫傳熱模型,并采用交流調制激勵、電阻串聯分壓、模數(A/D)轉換以及數字式正弦擬合方法獲取高精度傳感溫度的基礎上,選取二階低通數字濾波的合適阻尼系數與固有頻率,有效抑制隨機噪聲的影響,利用濾波結果進行微分預測補償,完成氣流溫度的快速動態測量。

1 數學模型

熱敏電阻的動態性能可用一階熱平衡方程加以描述,即傳感器熱量的變化與傳感器的吸熱率相等

(1)

式中k為液體和傳感器間的總傳熱系數,A為有效傳熱面積,m為傳感器質量,c為傳感器材料比熱,Tx為被測介質溫度,Ts為傳感器溫度,T0為初始時刻傳感器的溫度。可見,在考慮瞬態條件下的測量,傳感溫度與被測對象實際溫度存在較大差別。

式(1)可進一步改寫為

(2)

式中 時間常數τ=mc/kA,用以表示傳感器的熱響應時間。熱響應時間導致了傳感器溫度Ts的變化難以跟上被測介質溫度Tx的變化。

式(2)實現數字微分補償,要求離散采樣情況下代表dt的時間增量Δt很小,而此時代表dTs的ΔTs必然也應很小,一般傳感溫度代替實際溫度測量可以忽略的隨機誤差也可能導致Tx產生較大的誤差。因此,實現快速的動態測量,不僅要求準確測得時間常數,還要求保證獲取的傳感器溫度Ts具有很高的精度。

2 方 法

2.1 交流激勵測溫法

負溫度系數(negative temperature coefficient,NTC)熱敏電阻的基本溫度測量電路如圖1所示,其中,Vi為輸入信號,Vo為輸出信號,Rref為參考電阻,Rt為NTC熱敏電阻。

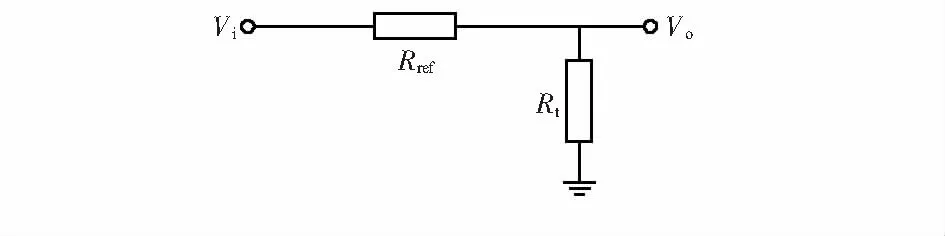
圖1 NTC熱敏電阻基本測溫電路

根據串聯分壓原理,熱敏電阻的阻值Rt可表示為

Rt=Vo×Rref/(Vi-Vo)

(3)

顯然,Rt的精度取決于Vo與Vi,因此，要求準確獲取Vo與Vi的值。采用交流調制激勵的方式,可以盡量消除電源噪聲與工頻干擾等的影響,提高Vo與Vi的測量精度。

通過直接數字合成(direct digital synthesis,DDS)方式產生的正弦交流信號[8],作為輸入信號Vi,其幅值為Ai。對輸入信號Vi與輸出信號Vo通過同步模/數轉換器(analog to digital converter,ADC)進行采樣,并利用數字正弦擬合處理采樣數據以得到其幅值Ai與Ao。

假設輸入信號Vi與輸出信號Vo可表示為

Vi=Ai×sin(ωt+φ1)

(4)

Vo=Ao×sin(ωt+φ2)

(5)

式中ω為角頻率,φ1與φ2分別為輸入信號與輸出信號的初始相位,理論上有φ1=φ2。

熱敏電阻的阻值Rt可重新表示為

(6)

最后,利用NTC熱敏電阻的阻值及其數學模型,即可推導出當前溫度T。NTC熱敏電阻與溫度的關系為

(7)

式中R0為參考溫度下的NTC熱敏電阻阻值；T0為參考溫度(一般選T0=298.15 K)；Bn為由電阻材料決定的熱敏指數。

2.2 交流信號處理方法

輸入與輸出信號通過A/D轉換后,均可獲得一組相應的采樣值序列Xn={x1,…,xi,…,xn},如圖2所示。

圖2 采樣值序列

為準確獲取它們的幅值信息Ai與Ao,采用最小二乘的正弦擬合方法。序列中的任一值可表示為

xi=Acos(Δi+φ)+C+εi

(8)

式中Δi為累積相位,即序列中第i點與第1點之間的相位差。由于采樣頻率與信號頻率都是已知量,Δi也是已知量。令

a=A×cosφ，b=-A×sinφ

(9)

則式(8)可進一步展開為

xi=acosΔi+bsinΔi+C+εi

(10)

根據最小二乘線性正弦擬合[9],a與b可表示為

a=-2∑xisinΔi/n，b=2∑xicosΔi/n

(11)

于是

(12)

得到幅值A后,即可根據式(6)與式(7)計算當前溫度。

2.3 預測濾波算法

在被測介質溫度連續變化時,盡管氣流溫度的變化可能較為迅速,但實際的溫度曲線仍然是連續光滑的,且沒有突變。為了消除溫度測量時的隨機誤差,設計了一種二階濾波算法。

二階低通濾波器的傳遞函數為

(13)

式中ζ為系統的阻尼比,ωn為系統無阻尼狀態下的固有頻率。

設濾波后溫度為Tf,則有

(14)

式中aTf為Tf的加速度,vTf為Tf的速度。

為便于在嵌入式環境下計算處理,需進行離散化,并利用如下的遞推公式,定義第i次的相關參數

(15)

式中ts為溫度采樣的時間間隔。

通過設置aTf,0與vTf,0為0,并設置合適的ζ與ωn,可以利用式(15)進行遞推運算以完成溫度數據的濾波,易于使用C語言實現。

進一步地,在標準實驗法獲取時間常數τ的基礎上[7],結合二階濾波的溫度變化速度的計算結果,利用式(2)進行微分補償,補償結果可表示為

Tp=Tf,i+τvTf,i

(16)

3 結果與分析

在測量前,將熱敏電阻由穩定的環境溫度(37.6 ℃)中迅速抽離并置入100 ℃的恒溫沸水中,以產生一溫度階躍信號,由此測出時間常數。然后將熱敏電阻放置于熱氣流管道中,并按一定的時間間隔給予不同的溫度擾動。由STM32F407的數/模轉換器(DAC)產生的頻率為40 kHz,直流偏置為1.25 V,幅值為610 mV的正弦輸入信號Vi；輸出信號Vo由STM32F407對應的ADC通道進行采集。利用前述方法求得測量的初步溫度數據,并經離散傅里葉變換(discrete Fourier transform,DFT),繪制如圖3所示的單側幅值頻譜圖。

圖3 單側幅值頻譜圖

觀察圖3可知,噪聲信號頻率主要在0.5 Hz以上,為有效濾除,需要設置合適的阻尼比ζ與固有頻率ωn。二階低通濾波器作為一個典型的二階系統,考察該系統在同一固有頻率時不同阻尼比的單位階躍響應以確定阻尼比。圖4為ωn=10,不同ζ的單位階躍響應。欠阻尼時,阻尼系數越小,超調量越大,上升時間越短,為保證較短的調整時間與適度的超調,這里，取ζ=0.7。

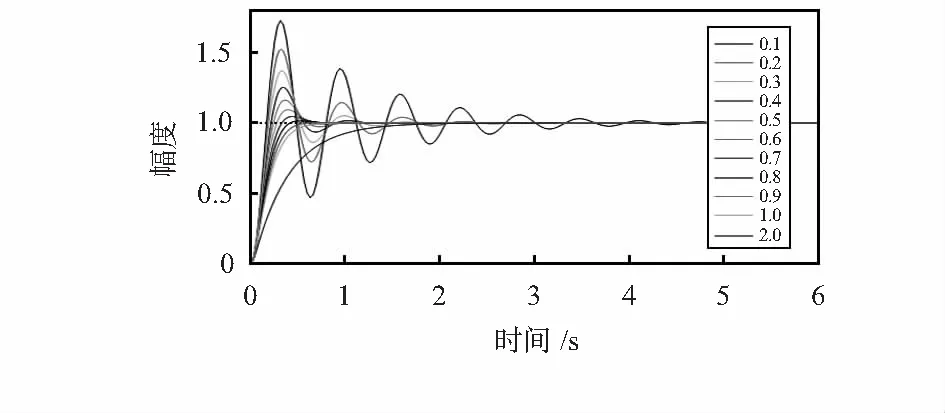
圖4 不同阻尼系數的單位階躍響應

二階低通濾波器的截止頻率隨ωn的減小而減小,因此ωn越小,對噪聲的抑制效果越好,但ωn過小會產生較大的滯后。圖5為不同固有頻率時的濾波效果,可見ωn=18時,濾波后的曲線較為光滑且沒有明顯滯后。

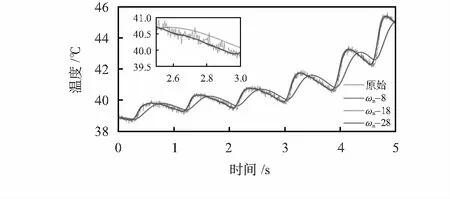
圖5 不同固有頻率時的濾波效果

濾波前后的溫度變化速率曲線如圖6所示,濾波后的速率曲線明顯更為光滑,更貼近于實際傳熱過程中的溫度變化情況。進一步地,利用濾波后的溫度變化速率及溫度,進行微分補償,補償結果如圖7所示,并將補償得到的峰值溫度與實際峰值溫度記于表1中。

圖6 濾波前后的溫度變化速率

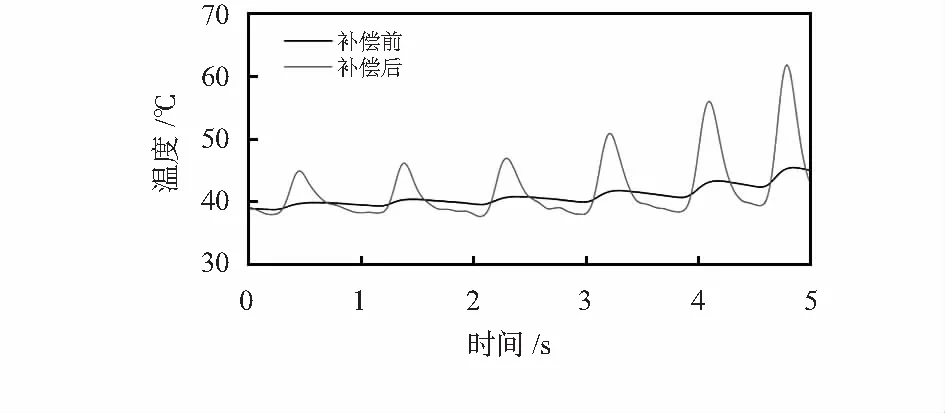
圖7 補償前后的溫度曲線

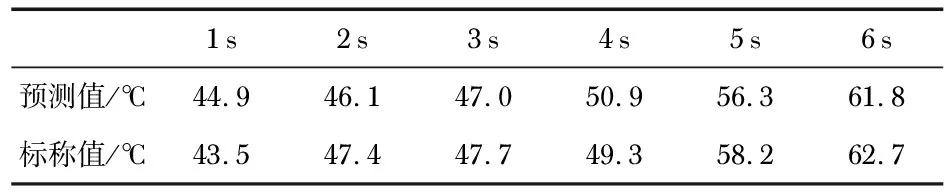
表1 峰值溫度

經過預測后,可以迅速達到預定的溫度峰值,并能在更短的時間內恢復到環境溫度,能較為正確地感受被測氣流的溫度擾動。

4 結 論

使用分壓電路與交流激勵的方式完成了溫度的采集,并使用二階低通濾波與數字微分預測對原始溫度數據進行處理,獲取了能正確反映氣流溫度快速擾動的預測溫度曲線,實現了在嵌入式環境下的溫度快速檢測。該方法簡單可行,靈活性高,適于快速溫度變化條件下的動態測量。