基于MCMC算法的Logistic回歸模型的參數估計
——以智能睡眠手環為例

趙斯穎

（西安財經大學統計學院，西安 710000）

0 引言

近年來，隨著馬爾可夫鏈蒙特卡羅（MCMC）方法的普及，越來越多的學者采用這種算法來模擬復雜的多元分布。在實際工作、學習中經常會遇到數據缺失、信息不全或者非標準化的多維隨機變量的抽樣問題，一般的抽樣方法很難對其進行處理，而MCMC方法就可以用來解決這類采樣難的問題。MCMC作為一種隨機抽樣方法，被廣泛應用于機器學習、深度學習和自然語言處理，其中包括Gibbs抽樣法和M-H算法。使用MCMC方法估計模型中的參數，就是構造一個以參數的后驗分布（目標分布）為平穩分布的馬爾可夫鏈，然后利用從平穩分布中提取的樣本點計算蒙特卡羅積分。

國內對模型的研究主要集中在其應用方面，對模型參數估計的研究相對較少，竇劍軍等采用Gibbs抽樣法對多元Logistic回歸模型的參數進行估計，最終得到的參數后驗分布為正態分布。蔣捷等利用MCMC算法中的Gibbs抽樣來推斷參數的后驗均值，以此來估計模型的參數。王純杰等采用M-H算法和切片Gibbs算法，計算Logistic回歸模型的后驗分布，結果表明這兩種方法都具有可行性。劉貞以貝葉斯分析為背景，討論了回歸模型系數變點相關問題，并采用MCMC方法對得到的貝葉斯估計進行實證模擬。

在經典統計中，通常用最大似然估計和最小二乘法來估計邏輯回歸模型的參數，在本文中，我們通過MCMC方法對Logistic回歸模型做參數估計，在對參數的先驗分布取正態分布時，推導出后驗聯合分布，并通過Python與MCMC相結合的方法對實際數據的擬合過程進行演示，對模型參數進行迭代，得到參數估計結果落在95%置信區間內，說明MCMC估計參數的結果是可靠的，從而證明模型的有效性。

1 模型描述

1.1 邏輯回歸模型

邏輯回歸（binomial logistic regression）是一個假設樣本服從伯努利分布，利用梯度下降法和極大似然估計求解的二分類模型。其看似是一種回歸算法，其實是分類算法，即已知許多特征，通過這些特征預測出類別的標簽。要確定它屬于哪個類別，就需要設置一個閾值，如果大于此閾值，則將其分配給一個類別；如果小于此閾值，則將其分配給另一個類別。二分類問題只有兩個標簽，記為條件概率（|），這里隨機變量的值是實數，而隨機變量的值通常是0或1，它的模型表示如下：

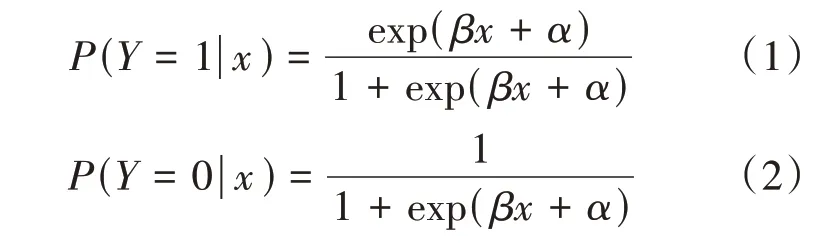
上式中∈R是輸入，∈{}0,1是輸出，∈R和∈R是參數，模型中的分類和值的正負是相關聯的。

1.2 馬爾可夫模型

馬爾可夫模型是一種基于馬爾可夫性質的統計模型，其假設在隨機過程中給定某一時刻狀態的概率分布，這個概率分布只與它前面的狀態有關，所以馬爾可夫鏈被廣泛應用在時間序列模型中。

用數字描述就是假設某一時間序列是…X,X,X,X,X…，在+1時刻的條件概率只與時刻有關，這也是馬爾可夫鏈模型一個非常有用的性質，即：

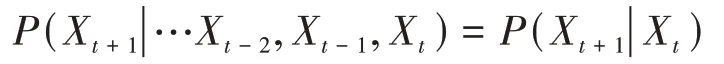
所以只要得到兩個狀態之間的轉換概率，就能計算出對應的概率分布的樣本。

馬爾可夫模型還包含隱馬爾可夫（HMM）、馬爾可夫鏈蒙特卡羅（MCMC）和馬爾可夫隨機場（MRF），其中MCMC和MRF被廣泛應用于模型參數的近似估計。

2 實證分析

2.1 睡眠數據分析

本文采集了智能手環中儲存了兩個多月的數據，將智能手環中的數據導出為csv文件格式，以便對數據進行建模。這里將智能手環的數據分為睡眠和清醒兩種狀態，手環主要根據擺動的頻率、次數或者佩戴者心律的變化來判斷睡眠和清醒狀態。

通過繪制睡眠數據的散點圖，我們可以更好地了解睡眠和清醒狀態的時間分布，如圖1所示，筆者通常在22點以后進入睡眠狀態，而僅有少部分入睡時間在22點以前。根據實際情況，0點以后入睡的概率很高（接近1），而21點以前入睡的概率很小，所以散點圖只描繪了從清醒到睡眠這段時間的狀態，即從21點到0點的數據分布。

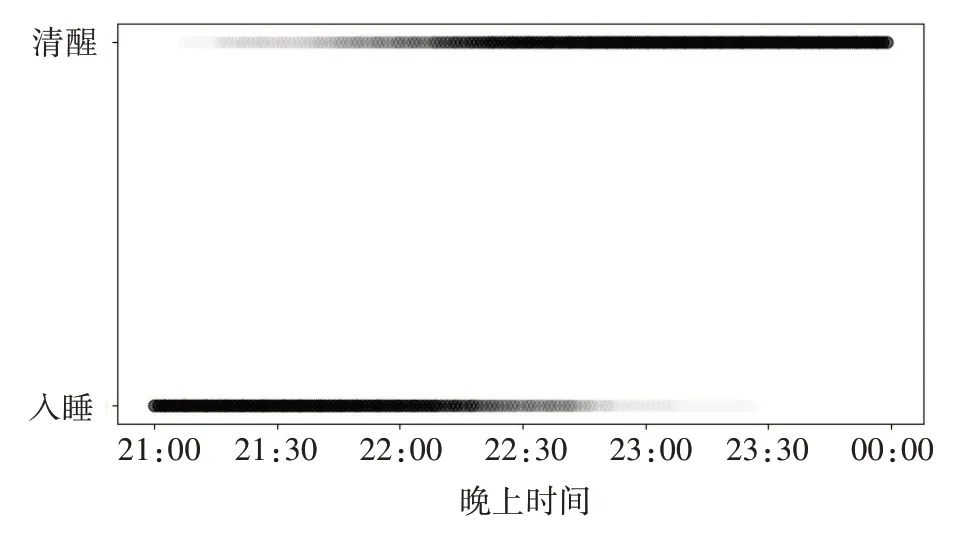
圖1睡眠數據分布

圖2 的清醒數據分布顯示，筆者的清醒時間大都集中在早晨6點以后，在5點至6點之間，大部分是處于睡眠狀態，比較符合實際情況。與上面睡眠數據分布同理，這里只展示從睡眠狀態轉換到清醒狀態的時間段，即早上5點至8點的數據分布，而8點以后清醒的概率非常高（接近1）。

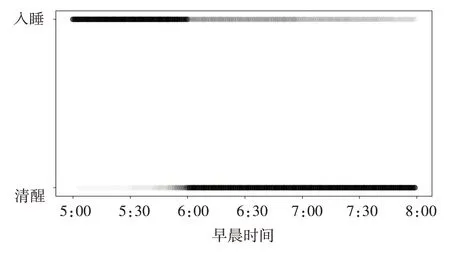
圖2 清醒數據分布

通過分析可知，在本例中一共包含入睡、清醒兩個狀態和一個時間維度，對于這種問題，通常可以使用邏輯函數對其進行建模：

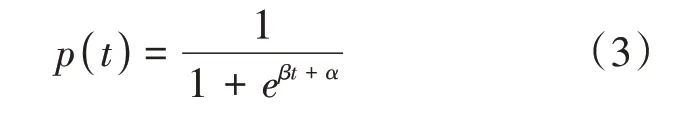
2.2 參數的先驗分布

我們對邏輯函數的參數α和取不同的值來觀察曲線的形狀，結構如圖3所示。

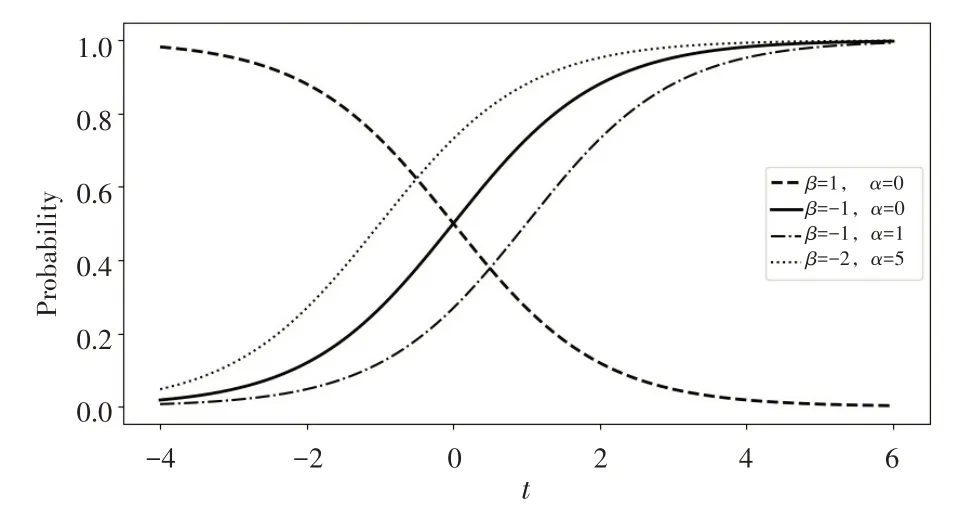
圖3 不同α和β參數的邏輯曲線

由圖3可知，當=0時，邏輯函數是一條型曲線，在曲線的中心位置增長速度較快；當＞0時，邏輯函數曲線向右偏移，由此只要找到合適的和參數就能很好地使用邏輯函數來擬合我們的數據。

因為參數的先驗分布事先是未知的，所以需要使用貝葉斯方法來找到合適的和。通常假設這兩個參數服從兩個正態分布，正態分布有兩個重要參數（均值）和（標準差），和的取值不同得到的正態分布曲線也不一樣，的取值可以是正數也可以是負數；而的值通常取正數。這里用另一個參數（精度）來替代，的取值是的倒數，所以正態分布的標準差和精度成反比，標準差越大，精度越低；標準差越小，精度越高。正太分布概率密度函數的定義如下：

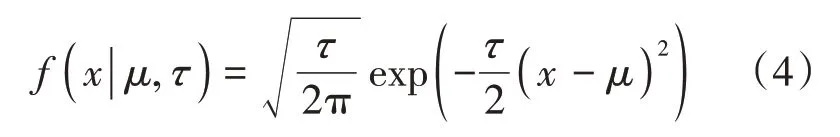
描繪出均值和精度完全不同的三組正態分布曲線，如圖4所示。可以看出，均值決定了圖形的中心對稱位置；精度決定了圖形的寬窄，取值越大，曲線越窄，分布精度越高；越小，曲線越寬，其分布精度也越低。

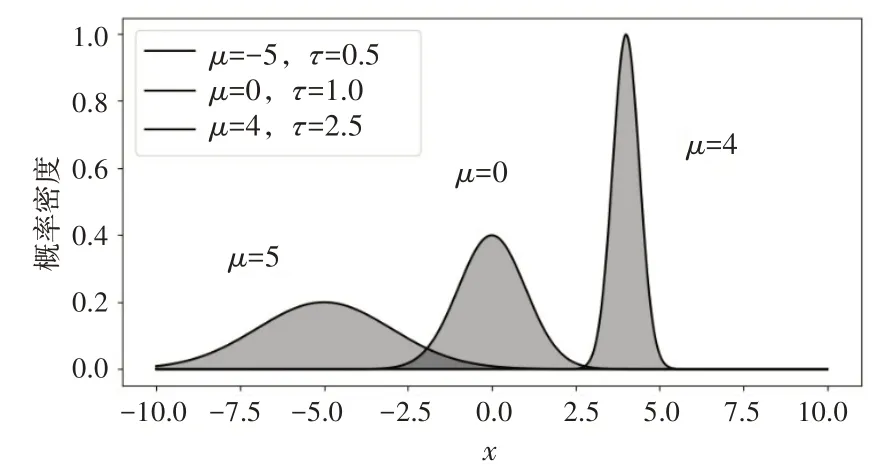
圖4 正態分布

2.3 馬爾可夫鏈蒙特卡羅

蒙特卡羅法又稱隨機抽樣法，是在概率模型的基礎上，通過計算機反復模擬得到近似解。而馬爾可夫蒙特卡羅（簡稱MCMC）是以馬爾可夫鏈為概率模型的蒙特卡羅法，它的核心是從一個已知概率密度函數的概率分布中進行采樣，來構造最接近真實數據的概率分布。

由于參數和我們無法直接計算，所以需要通過生成和的數千個樣本來構建最接近真實分布的近似值，邏輯函數的兩個參數和服從正態先驗概率，通過選擇隨機值，我們可以得到參數可能值的范圍，如圖5所示，越趨向于中心先驗概率就越高。

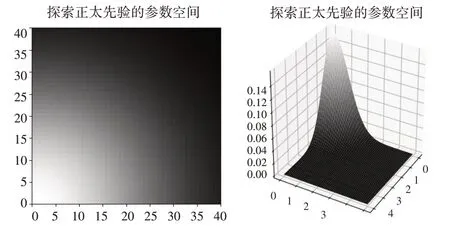
圖5 正態先驗的參數空間

正態分布的期望值是：

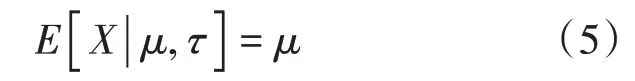
正態分布的標準差是：

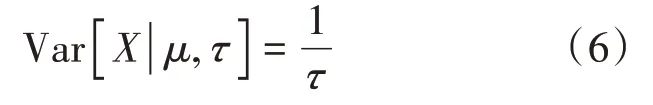
參數和服從正態分布，而正態分布的參數和具體數值未知，我們設定初始值=0、=0.05，利用MCMC對和進行抽樣，最大化和的似然度。

有多種方法可用來診斷MCMC的收斂性，這里主要介紹兩種檢驗方法。一種是Gelman檢驗，在給定置信水平為1的前提下，用每條鏈的軌跡區間1對應的長度除以整個軌跡區間長度作為診斷指數，當該指數接近1時就認為鏈收斂。另一種是軌跡圖檢驗法，通過查看采樣值路徑來判斷馬爾可夫鏈蒙特卡羅鏈在迭代過程中是否達到穩定狀態，收斂的馬爾可夫鏈形似白噪聲序列，在一個水平上沒有趨勢和周期的小幅波動。本文通過Pymc3提供的praceplot函數來繪制所有樣本的軌跡，結果如圖6所示。

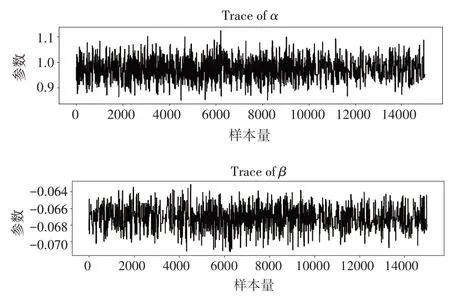
圖6軌跡圖

圖6 的軌跡圖直觀地展示了MCMC迭代過程中的采樣值，將迭代次數設定為14000，可以看到馬氏鏈迭代軌跡較平穩，并沒有出現明顯的波動周期性和異常值。

3 參數可視化

邏輯函數描述了從清醒到入睡的變化過程，但邏輯函數α和的真實值未知，通常假設α和來自于由和定義的正態分布，利用MCMC算法分別對參數α和采樣和,使得到的和最能接近真實數據的分布，對清醒和睡眠建模為一個伯努利變量，清醒用1表示，入睡用0表示。特定時間下入睡的伯努利變量由邏輯函數來定義：

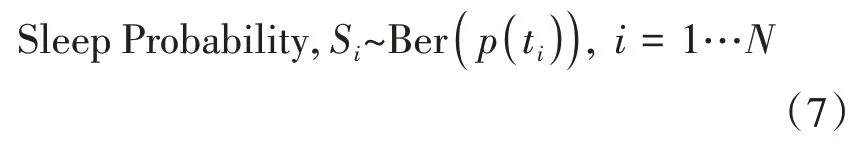
這里(t)為一個有獨立時間變量的邏輯函數，所以上面的公式也可以寫成：

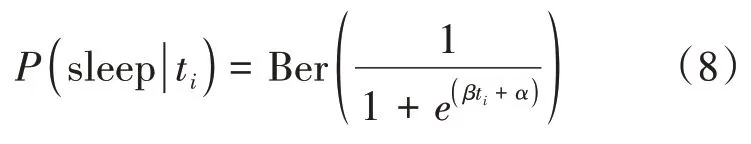
MCMC的目標是使用現有的數據找到α和參數，并假定它們來自于正態先驗。本文使用Python中功能強大的貝葉斯推理庫Pymc3，該庫包含了馬爾可夫鏈蒙特卡羅和其他推理算法，通過代碼創建模型并執行MCMC，為和抽取5000個樣本，指定的抽樣算法是Metropolic Hastings，我們將數據輸入模型，并設定模型數據為伯努利變量，模型為數據找到最有可能的參數和，跟蹤變量trace包含了所有后驗分布的樣本，據此可以對這些樣本進行可視化，以探索它們在采樣過程中的變化。隨著樣本的增加，MCMC算法收斂于最可能的值。在trace中返回的值都是參數的所有樣本，我們可以利用直方圖對這些值進行可視化，結果如圖7所示。

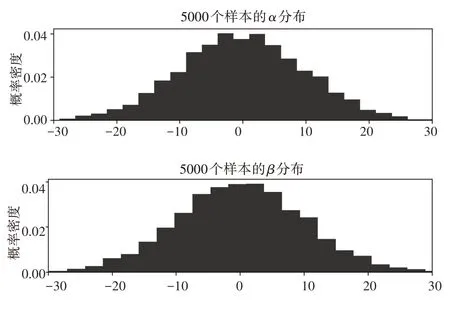
圖7 參數分布

從圖7可以看到，α、的均值比較接近0，從前面描繪的邏輯函數曲線圖來看，趨向于0時曲線趨于平坦，這說明清醒和睡眠的時間點存在重合的情況，這和實際情況相符，而α不等于0說明邏輯函數曲線發生了偏移，這也就意味著模型找到了一個從清醒到睡眠的轉折點，從睡眠數據的分布圖上看這個時間點應該是在晚上10點左右。

為了更加清楚地了解夜晚的睡眠狀況，本文描繪出5000個樣本數據的睡眠概率分布，如圖8所示。

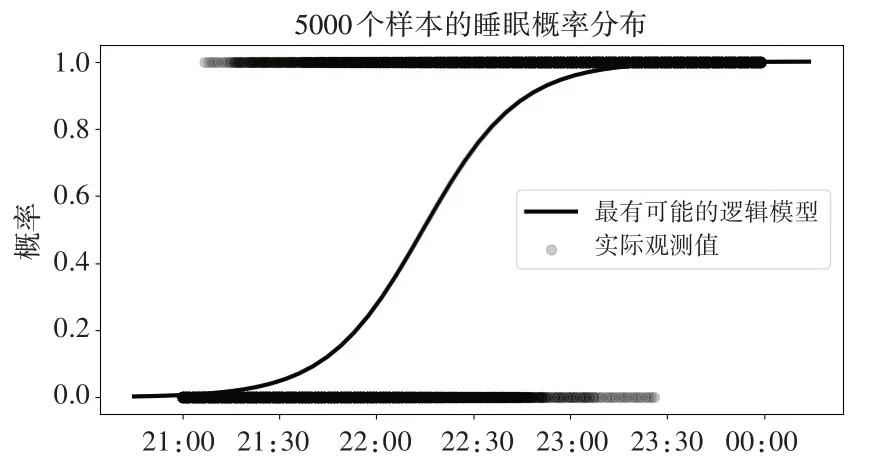
圖8 睡眠概率分布

從圖8可以看到，晚上9點半睡眠的后驗概率均值大概在0.00至0.08之間，這說明筆者在晚上9點半就入睡的可能性比較小，這符合實際情況，大多數成年人一般不會在9點半就入睡，不過10點半的睡眠概率突然增加到了0.74，這也比較符合現實情況。從之前的分析可知，睡眠概率大于0.5的轉折點是在晚上10點至10點半之間，也就是大部分成年人在這個時間點都會入睡，這應該比較符合常理。

4 結語

MCMC算法對整個統計學領域的研究有著深遠的影響，通過MCMC隨機模擬我們可以找到一個合適的模型來解決某些高維復雜的問題，特別是參數后驗分布的計算。本文將MCMC方法運用于具體的實例中，以正態分布函數為建議分布函數，采用M-H抽樣算法，運用Matlab對Logistic模型進行參數估計，通過構建睡眠模型讓筆者了解了自己的睡眠方式。有了以上的經驗，還可以根據其他數據信息，比如星期幾、日常活動如何影響我們的睡眠，本文對此假設并未深入研究，但這是使用貝葉斯方法分析真實數據的良好開端。