彈道明膠動態力學性能試驗與本構模型研究

蔣明飛， 許輝， 黃陳磊， 劉坤， 吳志林

(南京理工大學 機械工程學院， 江蘇 南京 210094)

0 引言

彈道明膠因其與人體肌肉組織相似的密度、黏彈性及良好的均勻性、透明性，在生物醫學和終點彈道中被廣泛用作軟組織模擬物。開展明膠動態力學性能試驗，建立其在高應變率下的本構模型，并將之應用于殺傷元侵徹明膠靶標的數值仿真工作，可更好地揭示殺傷元與明膠之間的相互作用機理。

明膠材料動態力學響應測試的難點在于明膠屬于低阻抗材料，低阻抗或軟材料的動態力學性能測試具有挑戰性，因為需要試樣均勻變形、測量大變形以及傳統的分離式霍普金森壓桿(SHPB)設備中可能出現低信噪比問題。幾十年來，一些學者對低阻抗或軟材料的動態力學性能測試做出了巨大貢獻。Chen等開發了新的SHPB技術，通過使用帶有端蓋的管狀透射桿或敏感的嵌入式儀器來測試低阻抗材料。盧芳云等采用波形整形技術，實現了軟材料試樣在實驗過程中的應力平衡和常應變率加載。Cronin等曾使用聚合物分離式霍普金森壓桿(PSHPB)來測試低阻抗材料的動態特性。此外，文獻[14-16]分析了應力波在黏彈性桿中傳播時的彌散和衰減。

國內外多位學者曾對明膠材料開展了力學性能測試試驗及本構模型研究。劉麗對4 ℃環境下10%明膠開展了基礎性的壓縮、剪切流變實驗，獲得一系列線性、非線性黏彈性參數和破裂特性。文獻[18-20]發現明膠是一種黏彈性和非線性的材料，并且對應變率高度敏感，因為明膠中的應力水平在準靜態和動態壓縮載荷之間存在很大差異。文獻[21-22]對明膠在較寬的應變率范圍內進行了力學行為測試，并提出了兩種本構模型來預測材料的力學響應。Salisbury等使用PSHPB裝置獲得了明膠在1 000～4 000 s應變率范圍的力學性能。文獻[24-25]均使用壓電薄膜傳感器的測試方法獲取彈道明膠的動態力學特性。Liu等建立了朱- 王- 唐本構模型來描述明膠在超高應變率下的力學響應。上述研究因測量方法和手段的不同，動態力學特性結果差異性較大，出現這一現象的原因尚不明確。

本文為解決明膠材料在動態力學測試中出現的低信噪比、非均勻變形等問題，SHPB裝置選用鋁合金壓桿搭配半導體應變片，同時采用波形整形技術及薄片試樣等手段，獲得了4 ℃環境下10%和20%彈道明膠在應變率1 500～4 000 s范圍內的動態力學特性。此外，建立了考慮應變率效應的多項式本構模型來預測明膠在高應變率下的力學行為，并通過數值仿真驗證了本構模型的正確性。

1 動態力學性能試驗

自1949年Kolsky發明SHPB裝置以來，它已成為測試材料動態性能最廣泛使用和最有效的裝置。為解決傳統SHPB裝置在測量軟材料時的波阻抗不匹配問題，大多數學者的方法是采用PSHPB技術，但聚合物桿將黏彈性效應引入了系統，引起波的彌散和衰減，使得應力波在入射桿和透射桿中傳播會發生畸變，分析將變得更加困難和繁瑣。此外，聚合物桿容易受到溫度和濕度的影響而老化，試驗的一致性很難保證。本文采用LC4超高強度鋁合金作為壓桿材料，使壓桿與試件之間的波阻抗盡可能匹配，并允許進行彈性應力波分析。

SHPB試驗裝置的示意圖如圖1(a)所示，入射桿、透射桿的直徑和長度均為14.5 mm和1 500 mm，撞擊桿的長度選取將在后文中討論。采用波形整形技術延長入射波的上升沿時間，確保試樣沿長度方向的均勻變形。選用半導體應變片來測量透射波信號，半導體應變片的優勢在于它的靈敏度是金屬應變片的50倍。圖2比較了兩種應變片測量透射波信號的效果，金屬應變片測量的信號容易被噪聲湮沒，而半導體應變片工作時具有良好的試驗效果。明膠動態力學性能測試的試驗場景如圖1(b)所示。為監測試樣的變形過程，特別是在動態加載過程中試樣的尺寸變化，使用了高速攝影機(美國VIsion Research公司生產的Phantom v2511)，拍攝頻率為125 000幀/s，曝光時間為7 μs。

圖1 測試裝置組成及試驗場景Fig.1 Testing device and test site

圖2 兩種應變片測量的透射波信號效果對比Fig.2 Comparison of transmission pulse signals measured by two types of strain gauges

美國和國內眾多軍工單位均使用4 ℃環境下、10%濃度的明膠作為仿生靶標。本文制作了4 ℃環境下濃度為10%和20%的兩種明膠。將照相明膠顆粒與自來水分別按1∶9和2∶8質量配比，置于恒溫60 ℃的水浴爐中保溫1 h，然后將明膠溶液注入模具，置于4 ℃恒溫箱中保溫24 h。制備了兩種規格尺寸的10%明膠試樣，圓形薄片試樣尺寸為10 mm×2 mm，較厚試樣尺寸為10 mm×5 mm。圖3為試驗中一組10%明膠薄片試樣。

圖3 10%明膠薄片試樣Fig.3 10% gelatine slice specimens

2 試驗結果

在正式開展試驗之前，進行一組初始測試，以確保試樣的變形處于恒定應變率。撞擊桿的長度選擇對實現恒定應變率加載有重要影響。選取10%明膠試樣對50 mm、100 mm、200 mm和400 mm四種長度的撞擊桿分別進行了測試，以對比不同長度撞擊桿的效果。圖4為使用不同長度的撞擊桿測試得到的10%明膠的應變率，從中可見使用長度為400 mm的撞擊桿，可實現明膠材料的恒定應變率加載。因此，最終選取長度為400 mm的撞擊桿進行試驗。

圖4 不同長度的撞擊桿測試得到的10%明膠的應變率對比Fig.4 Comparison of strain rates of 10% gelatine with different striker lengths

波形整形器在低阻抗材料的測試中發揮著重要作用，有利于實現試樣的應力平衡和恒定應變率加載。圖5展示了不同的波形整形材料，包括6層總厚度為1.4 mm的紫銅片、1層總厚度為4.0 mm的瓦楞紙板和10層總厚度為2.5 mm的醫用膠布。

圖5 不同的波形整形材料Fig.5 Different pulse-shaping materials

不同波形整形材料的整形效果對比如圖6所示。未使用波形整形器的原始波形接近方波，并伴有振蕩且不平滑。使用紫銅片整形的波形類似于三角波，但不太規則。使用醫用膠布整形的波形相對規則且具有相對平滑的上升沿。而用瓦楞紙板整形后的波形相對于其他波形，具有平滑的上升沿和明顯的平臺段，有助于實現應力平衡和恒定應變率加載。因此，最終選擇4 mm厚的瓦楞紙板作為波形整形器材料。

圖6 波形整形效果對比Fig.6 Comparison of pulse-shaping effects

為降低試樣初始加載階段的徑向慣性效應，需要合理設計試樣尺寸的長徑比。本文采用尺寸為10 mm×2 mm(直徑與長度比為5∶1)的明膠薄片試樣。區別于準靜態測試，動態測試采用的試樣厚度明顯較小，因為在動態加載期間試樣兩側需要保持相同的應力水平(即動態應力平衡)。明膠材料的聲速約為1 500 m/s，在2 mm厚的試樣中波傳播時間約為1.3 μs。當用瓦楞紙板作為波形整形器材料時，應力波在明膠試樣中來回反射大約 40次，足以實現動態應力平衡。圖7為采集到的撞擊桿速度為7.41 m/s時的波形信號。由圖7可以看出，在加載和卸載部分都實現了動態應力平衡，反射波的平臺段代表了恒定應變率加載。

圖7 撞擊桿速度為7.41 m/s時的波形信號Fig.7 Pulse signals with a striking velocity of 7.41 m/s

用高速攝影機監測明膠試樣在動態載荷下的壓縮變形，較厚尺寸(10 mm×5 mm)的試樣用來比較明膠動態壓縮過程中的變形。明膠薄片試樣(10 mm×2 mm)在加載過程中基本均勻變形，而在較厚的明膠試樣中捕捉到了明顯的非均勻變形，如圖8所示，圖中入射桿端面(左側)的試樣直徑明顯大于透射桿端面(右側)。

圖8 較厚明膠試樣的非均勻變形現象Fig.8 Non-uniform deformation of the thicker gelatine specimen

在確定了撞擊桿長度、波形整形器材料和試樣尺寸后，優化后的SHPB裝置證明適用于測量軟質明膠材料的動態力學行為。每個應變率在相同的測試條件下重復5次試驗，以保證試驗的可靠性。明膠在不同應變率下的真實應力- 真實應變曲線如圖9所示，從中可以看出明膠的動態力學響應是非線性的且與應變率相關。不同應變率下的應力- 應變曲線存在相似性，以10%明膠在4 000 s和20%明膠在3 500 s應變率下的應力- 應變曲線為例，按曲線的變化趨勢可劃分為4個階段：Ⅰ—彈性段，Ⅱ—塑性強化段1，Ⅲ—塑性強化段2，Ⅳ—塑性強化段3。在彈性段，應力和應變呈線性關系且滿足胡克定律，彈性段直線的一致性較好，說明彈性模量隨應變率變化不明顯。彈性段結束時，存在由彈性段向塑性段轉變的屈服點，進入塑性強化段1后，應力隨著應變的增加而緩慢增加，此階段塑性強化效應不明顯。當進入塑性強化段2后，材料呈現明顯的塑性強化效應，應力隨應變的增加而急劇增加。當進入塑性強化段3后，此階段一開始塑性強化效應較強，但隨著應變的增加，強化效應逐漸減弱。此外，在相似的應變率下，20%明膠比10%明膠表現出更高的應力水平。

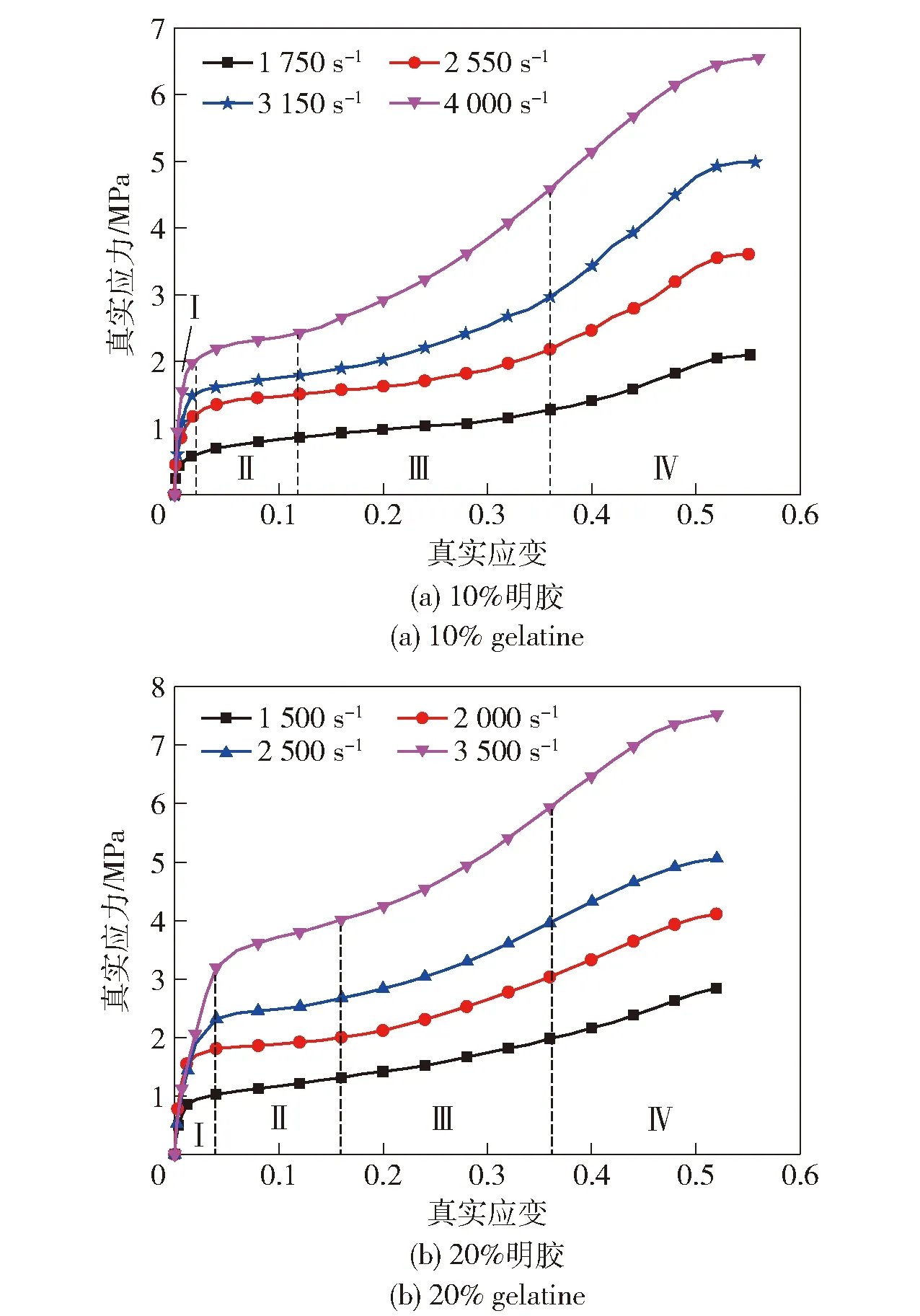
圖9 明膠在高應變率下的應力- 應變曲線Fig.9 Stress-strain curves of gelatine at high strain rates

明膠的屈服強度隨應變率對數的變化規律如圖10所示。由圖10可見：在1 500～4 000 s的應變率范圍內，明膠材料的屈服強度在0.6～3.2 MPa之間變化，反映出明膠材料對應變率敏感，屈服強度隨著應變率對數的增加而增加；相似應變率下，20%明膠的屈服強度均高于10%明膠，表明增加應變率及濃度均會提高明膠材料的強度。

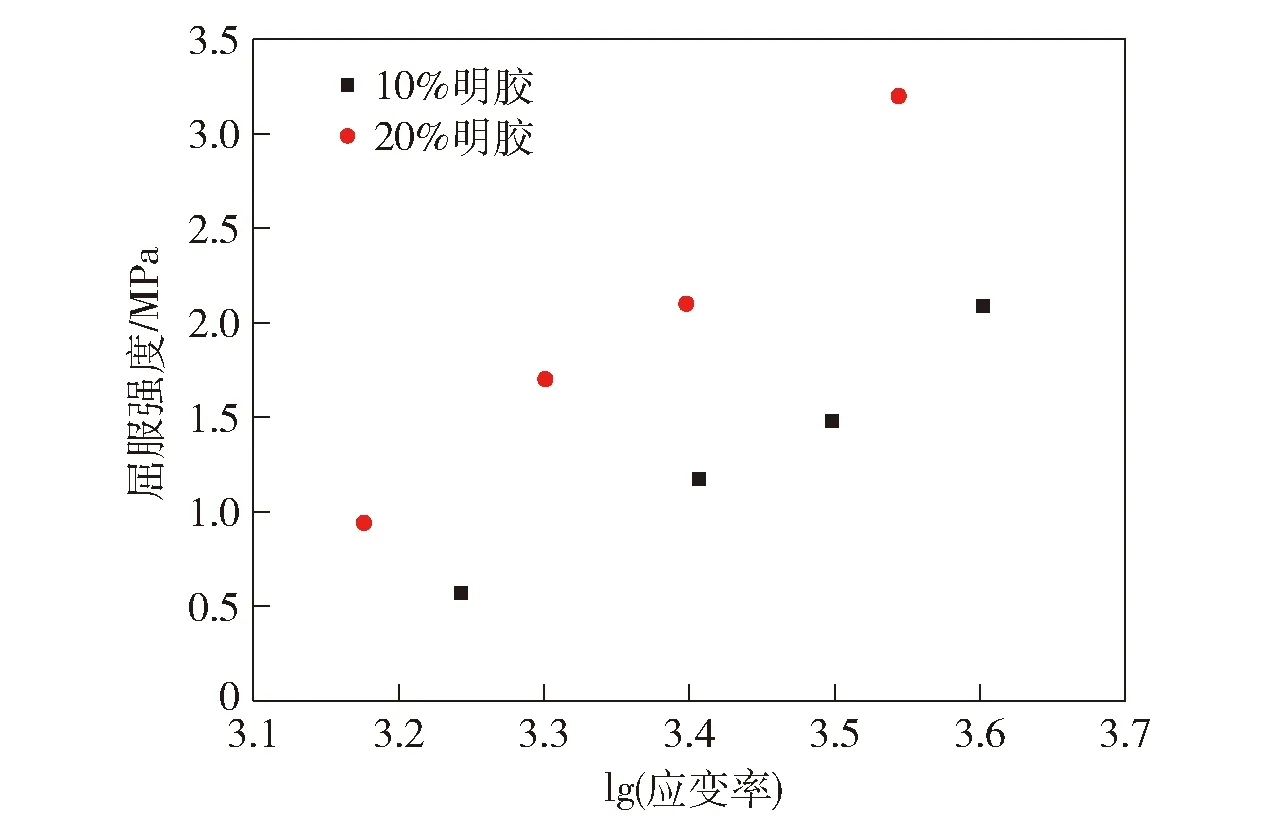
圖10 明膠在高應變率下的屈服強度Fig.10 Yield strength of gelatine at high strain rates

將本文采用金屬桿與Kwon等、Salisbury等采用非金屬桿測得的10%明膠的力學性能進行對比分析，如圖11所示。由圖11可見3組數據在相似應變率下的差異性較大：在應變0～0.6之間，Kwon等測得的明膠中應力水平較高，Salisbury等測得的明膠中應力水平偏低，而本文采用金屬桿測得的明膠應力幅值介于Kwon等和Salisbury等之間；當應變超過0.6以后，Salisbury等數據中的應力隨應變的增加而急劇增加，其測得的應力峰值是本文與Kwon等數據的4～6倍。推斷造成上述差異性的原因：采用非金屬桿需要對波的彌散和衰減進行修正，修正誤差較大；與金屬桿相比，非金屬桿容易受到溫度和濕度的影響而老化，試驗的一致性很難保證。

圖11 采用金屬桿與非金屬桿測試10%明膠的力學性能對比Fig.11 Mechanical properties of 10% gelatine tested with metal bars and non-metal bars

3 本構模型

3.1 模型建立

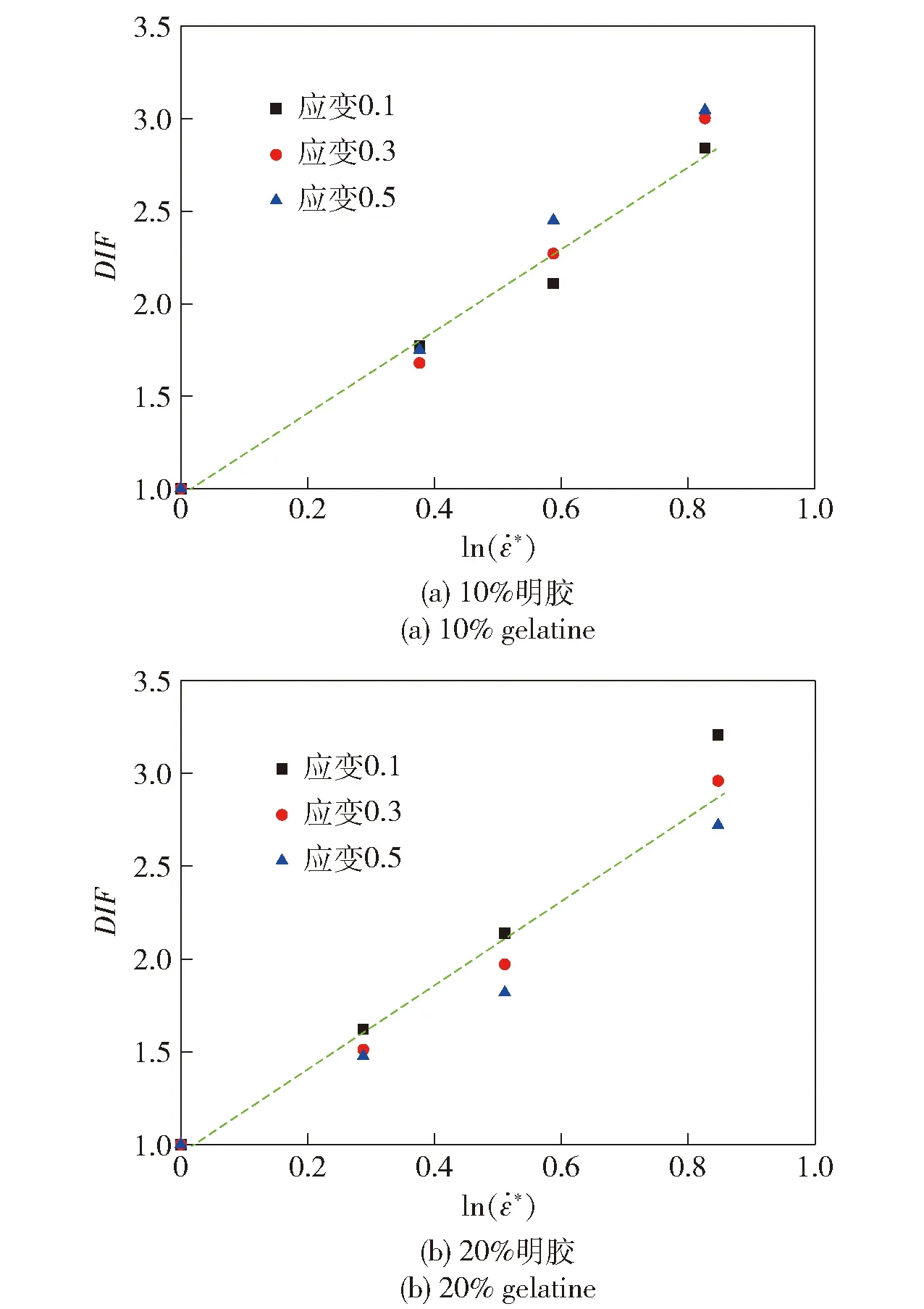
圖12 明膠中應力的動態增長因子Fig.12 Dynamic increase factor of stress in gelatine

歸一化應變率的對數表達式為

(1)

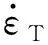
根據DIF曲線的變化趨勢及相關分析，可使用以下線性形式來擬合：

(2)

式中：和為擬合系數，具體計算值如表1所示。

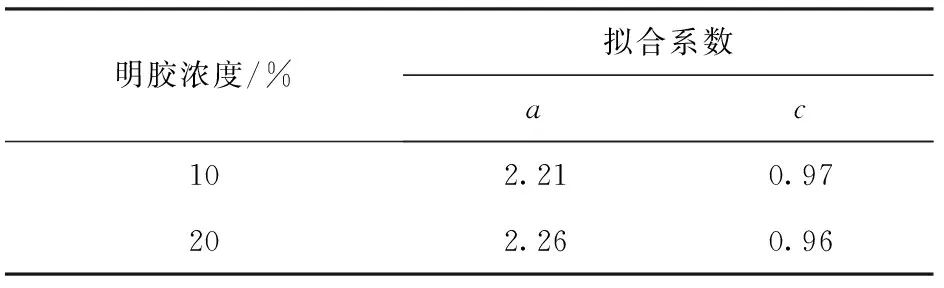
表1 根據試驗測試數據擬合的系數a和cTable 1 Coefficients a and c fitted to experimental data

在嘗試多種模型擬合后，發現修正的6階多項式模型適合描述明膠的動態力學行為，本構模型的表達式為

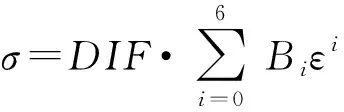
(3)

式中：為真實應力；為真實應變；為階數；為擬合系數，計算結果如表2所示。

表2 明膠的本構模型擬合系數Table 2 Fitting parameters of the constitutive model of gelatine MPa

3.2 模型驗證

基于所建10%明膠的本構模型，利用FORTRAN環境編譯進行材料模型的二次開發，借助有限元軟件LS-DYNA，開展球形破片侵徹明膠的數值仿真。數值仿真模擬了前期研究的兩個實驗工況：直徑為4.8 mm的鋼球分別以754 m/s和980 m/s的初速，侵徹尺寸為350 mm×250 mm×200 mm的10%明膠塊。數值仿真中，鋼球和明膠均采用三維拉格朗日實體單元(SOLID 164)，鋼球采用剛體材料模型(*MAT_RIGID)，明膠采用自定義材料模型(*MAT_USER_DEFINED_MATERIAL_MODELS)。面面侵蝕接觸算法，用于模擬球體與明膠之間的相互作用；設置黏性沙漏控制，保證大變形計算速度和準確性。劃分網格后的有限元模型如圖13所示。

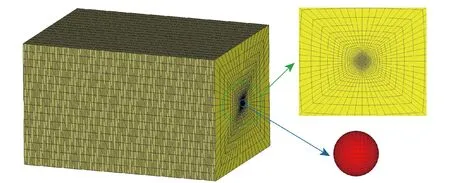
圖13 有限元網格模型Fig.13 Meshed finite element model

圖14為鋼球以754 m/s初速沖擊時不同時刻的明膠中形成的瞬時空腔。由圖14可見，數值仿真與試驗的空腔輪廓相似，且在空腔的長度及直徑上基本吻合，說明數值仿真能較好地模擬明膠中的瞬時空腔膨脹情況。

圖14 試驗(左)及仿真(右)瞬時空腔對比Fig.14 Comparison of temporary cavity values obtained from experiment (left) and simulation (right)

數值仿真與試驗獲得的鋼球侵徹明膠深度的對比如圖15所示。由圖15可見，鋼球以初速980 m/s沖擊，在0.8 ms、1.2 ms和1.6 ms時，侵徹深度的仿真值與試驗值的誤差分別為2.2%、4.9%和3.8%，可見侵徹深度的仿真值與試驗值的最大誤差在5%以內，說明數值仿真可以較好地模擬鋼球在明膠中的運動變化規律。由此可見，本文所建的明膠本構模型具有可靠性。

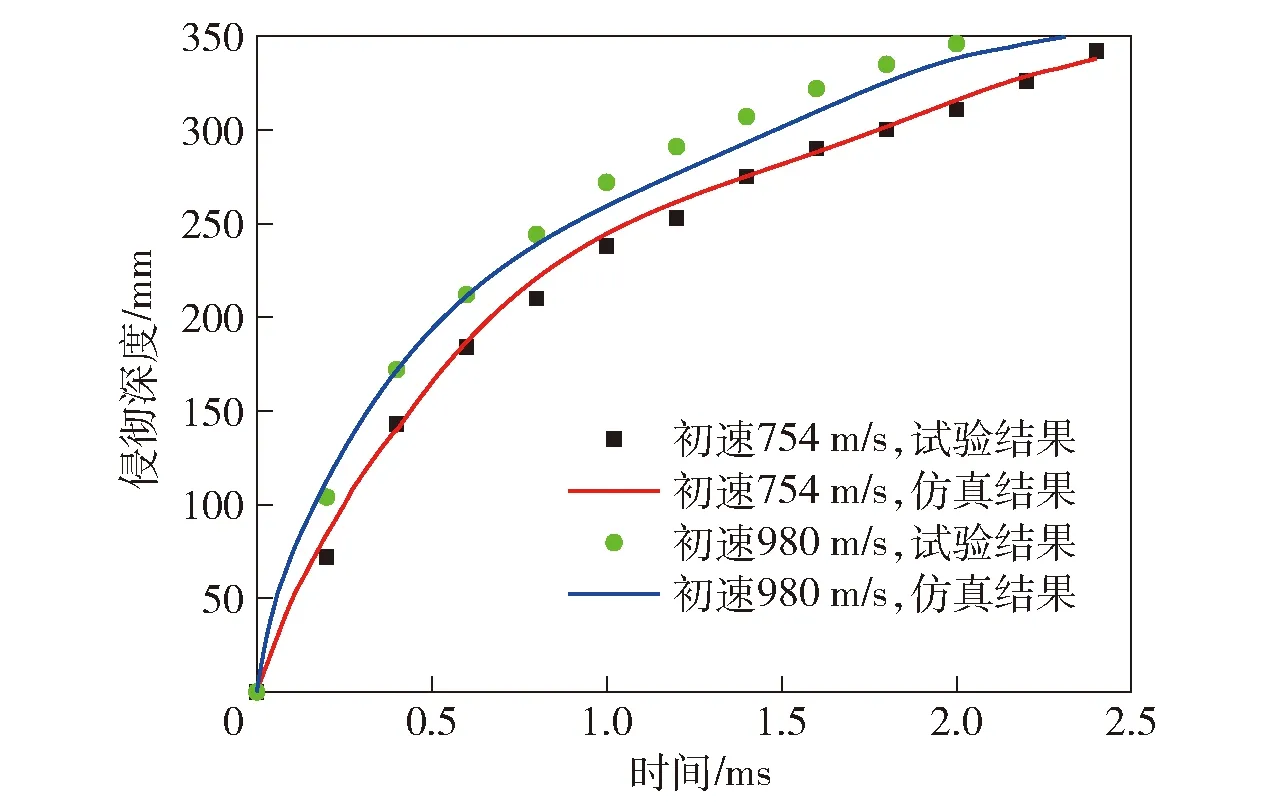
圖15 仿真與試驗結果的侵徹深度對比Fig.15 Comparison of penetration depths obtained from experiment and simulation

4 結論

本文對4 ℃環境下濃度10%和20%彈道明膠的動態(1 500～4 000 s)力學特性展開了試驗研究。為解決明膠材料在動態力學測試中出現的低信噪比、非均勻變形等問題，SHPB裝置選用鋁合金壓桿搭配半導體應變片，同時采用波形整形技術及薄片試樣等手段。得出主要結論如下：

1)明膠的力學響應是非線性的且高度依賴于應變率，應力- 應變曲線由彈性段及三個塑性強化段組成。

2)應力動態增加因子與歸一化應變率的對數呈線性關系。

3)考慮了應變率效應的多項式本構模型能較好地描述明膠在高應變率下的力學行為。

研究成果可為輕武器殺傷元侵徹明膠靶標的數值仿真工作提供支撐。