基于正交試驗(yàn)的粉煤灰-硅錳渣再生混凝土力學(xué)性能研究

王晨晨，王學(xué)志，陳東林，賀晶晶

(1.遼寧工業(yè)大學(xué)土木建筑工程學(xué)院，錦州 121001；2.中國(guó)電建集團(tuán)西北勘測(cè)設(shè)計(jì)研究院有限公司，西安 710100)

0 引 言

固體廢棄物多為工業(yè)生產(chǎn)的副產(chǎn)品，如粉煤灰、礦渣、尾礦、煙塵、灰燼等，當(dāng)前對(duì)固體廢棄物的處理方式多以堆積和填埋為主，這不僅會(huì)加重環(huán)境負(fù)擔(dān)，而且會(huì)使填埋導(dǎo)致的金屬元素滲入水中而污染周圍環(huán)境。在全球范圍內(nèi)，混凝土是生產(chǎn)量最大的建筑材料之一，若可以利用這些固體廢棄物制備再生混凝土，不僅可以降低對(duì)大氣和土地的污染，還將降低混凝土的生產(chǎn)成本[1-3]。

水泥是混凝土中最基本的黏結(jié)材料，也是建材中消耗量最高的材料。粉煤灰自身的火山灰特性和在混凝土中發(fā)生的二次水化反應(yīng)使其可以取代水泥熟料用于混凝土中；河砂由于優(yōu)異效果和易獲得性被廣泛用作細(xì)骨料，但過(guò)度疏浚河砂會(huì)嚴(yán)重影響水生生態(tài)系統(tǒng)，硅錳渣與河砂化學(xué)成分近似[4-5]，且滿足《普通混凝土用砂、石質(zhì)量及檢驗(yàn)方法標(biāo)準(zhǔn)》(JGJ 52—2006)[6]基本要求，有作為細(xì)骨料取代部分河砂用于混凝土的可能性；天然骨料在混凝土中占比高達(dá)40%(質(zhì)量分?jǐn)?shù))，且是不可再生資源，隨著國(guó)家城鎮(zhèn)化進(jìn)程的推進(jìn)，廢舊房屋的拆除使建筑垃圾日益增多，約占總固體廢棄物的一半，通過(guò)對(duì)建筑垃圾進(jìn)行破碎、清洗、篩選等工序得到的再生骨料是天然粗骨料的最佳取代物，這也是建筑垃圾循環(huán)再利用的最佳方式[7]。

本文用粉煤灰、硅錳渣、再生骨料制備粉煤灰-硅錳渣再生混凝土，為進(jìn)一步研究粉煤灰取代膠凝材料、硅錳渣取代砂和再生骨料取代粗骨料對(duì)混凝土力學(xué)性能的影響，設(shè)計(jì)了粉煤灰、硅錳渣、再生骨料在不同取代量下的三因素四水平正交試驗(yàn)，對(duì)混凝土的坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度進(jìn)行了分析。

1 實(shí) 驗(yàn)

1.1 原材料

1.1.1 膠凝材料

水泥為P·O 42.5硅酸鹽水泥，粉煤灰為Ⅰ級(jí)粉煤灰，具體化學(xué)組成見(jiàn)表1。

表1 水泥和粉煤灰的化學(xué)組成

1.1.2 細(xì)骨料

砂為錦州當(dāng)?shù)睾由埃?xì)度模數(shù)為2.4，堆積密度為1 868 kg/m3；硅錳渣為錦州當(dāng)?shù)啬骋苯饛S生產(chǎn)后的廢棄物，經(jīng)水淬冷卻得到，細(xì)度模數(shù)為2.8，堆積密度為1 500 kg/m3，具體化學(xué)組成見(jiàn)表2，各粒徑篩余量見(jiàn)表3。

表2 硅錳渣的化學(xué)組成

表3 硅錳渣各粒徑篩余量

1.1.3 粗骨料

粗骨料為5～20 mm連續(xù)粒徑的天然碎石；再生骨料由C30～C50廢舊混凝土經(jīng)破碎篩選得到，粒徑為5～20 mm，壓碎指標(biāo)為15.4%。

1.1.4 其他

減水劑為湖南某建材公司生產(chǎn)的聚羧酸減水劑，固含量為40%，減水率為25%。

1.2 試驗(yàn)設(shè)計(jì)

為高效研究工業(yè)固體廢棄物取代量對(duì)混凝土力學(xué)性能的影響，采用正交試驗(yàn)，考慮因素為粉煤灰取代水泥量F(體積分?jǐn)?shù)，下同)，硅錳渣取代砂量S(體積分?jǐn)?shù)，下同),再生骨料取代天然粗骨料量R(質(zhì)量分?jǐn)?shù)，下同)，每個(gè)因素設(shè)置四個(gè)水平，即試驗(yàn)因素和水平為三因素四水平，正交試驗(yàn)表的設(shè)計(jì)采用L16(45),設(shè)置兩列空列進(jìn)行研究，試驗(yàn)設(shè)計(jì)如表4所示。C40基準(zhǔn)混凝土配合比見(jiàn)表5。

表4 正交試驗(yàn)因素和水平

表5 C40基準(zhǔn)混凝土配合比

1.3 試驗(yàn)準(zhǔn)備及試件制作

用直徑4.75 mm的砂用篩過(guò)篩得到硅錳渣；將再生骨料在水中浸泡24 h，撈出曬至表面無(wú)明水，即處于飽和面干燥狀態(tài)；將減水劑直接倒入水中拌勻使用。在拌和時(shí)采用與常規(guī)混凝土拌和不同的加料順序，即先將細(xì)骨料與膠凝材料加水(含減水劑)拌和2 min，再倒入粗骨料和水(含減水劑)拌和1 min，最終加入剩余水(含減水劑)繼續(xù)拌和2 min，制得粉煤灰-硅錳渣再生混凝土。采用與常規(guī)混凝土不同的加料順序是因?yàn)楫?dāng)作細(xì)骨料使用的硅錳渣疏松多孔，沒(méi)有天然河砂的級(jí)配良好，為了防止混凝土成型時(shí)出現(xiàn)泌水現(xiàn)象，讓其先與膠凝材料混合，填充部分空隙后再進(jìn)行混凝土拌和成型。每組配合比制備6個(gè)尺寸為100 mm×100 mm×100 mm的立方體試塊，放在溫度為(20±3)℃、濕度大于95%的標(biāo)準(zhǔn)環(huán)境中養(yǎng)護(hù)28 d，進(jìn)行立方體抗壓強(qiáng)度試驗(yàn)和劈裂抗拉強(qiáng)度試驗(yàn)。

混凝土坍落度測(cè)試依據(jù)《普通混凝土拌合物性能試驗(yàn)方法標(biāo)準(zhǔn)》(GB/T 50080—2016)進(jìn)行，混凝土力學(xué)性能測(cè)試依據(jù)《混凝土物理力學(xué)性能試驗(yàn)方法標(biāo)準(zhǔn)》(GB/T 50081—2019)進(jìn)行，采用YAW-50000J型壓剪試驗(yàn)機(jī)作為加載設(shè)備。

2 結(jié)果與討論

2.1 試驗(yàn)結(jié)果

C40基準(zhǔn)混凝土和粉煤灰-硅錳渣再生混凝土的坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度試驗(yàn)結(jié)果見(jiàn)表6。由表6可知：SRC-1抗壓強(qiáng)度最高，較基準(zhǔn)組降低了8.0%，SRC-12抗壓強(qiáng)度最低，較基準(zhǔn)組降低了19.7%；SRC-1劈裂抗拉強(qiáng)度最高，較基準(zhǔn)組降低了2.2%，SRC-15劈裂抗拉強(qiáng)度最低，較基準(zhǔn)組降低了44.8%。將表6中的試驗(yàn)結(jié)果用SPSS進(jìn)行數(shù)據(jù)分析，得到混凝土坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度的極差分析和方差分析結(jié)果,分別見(jiàn)表7和表8。

表6 C40基準(zhǔn)混凝土和粉煤灰-硅錳渣再生混凝土坍落度和強(qiáng)度試驗(yàn)結(jié)果

表7中Kij表示第i個(gè)因子在第j個(gè)水平因素影響下的試驗(yàn)結(jié)果，計(jì)算公式如式(1)所示。

(1)

式中：m指具體試件，i表示因子，j表示因子的水平，即Bij，m表示第m個(gè)試件的第i個(gè)因子在第j個(gè)水平因素影響下的試驗(yàn)測(cè)試結(jié)果，n為第i個(gè)因子在第j個(gè)水平因素影響下的計(jì)算結(jié)果的個(gè)數(shù)。

Ri表示第i個(gè)因子在j個(gè)水平下最大值與最小值的差，計(jì)算公式如式(2)所示。

Ri=max{Kij}-min{Kij}

(2)

由表7可以看出，粉煤灰、硅錳渣和再生骨料對(duì)粉煤灰-硅錳渣再生混凝土坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度的極差影響都大于空列的影響，說(shuō)明正交試驗(yàn)的結(jié)果是可信的，三種材料對(duì)混凝土力學(xué)性能影響的變化規(guī)律值得參考, 這與黃鑫等[8]的結(jié)論一致。

表7 粉煤灰-硅錳渣再生混凝土坍落度和強(qiáng)度的極差分析檢驗(yàn)

表8中的Fv值為統(tǒng)計(jì)量，是指在顯著性水平0.05，組間自由度和組內(nèi)自由度分別為3、6情況下，函數(shù)的臨界分布值，為F0.05(3,6)=4.76。當(dāng)Fv值大于4.76時(shí)，為顯著性影響因素；當(dāng)Fv值小于4.76時(shí)，為非顯著性影響因素。

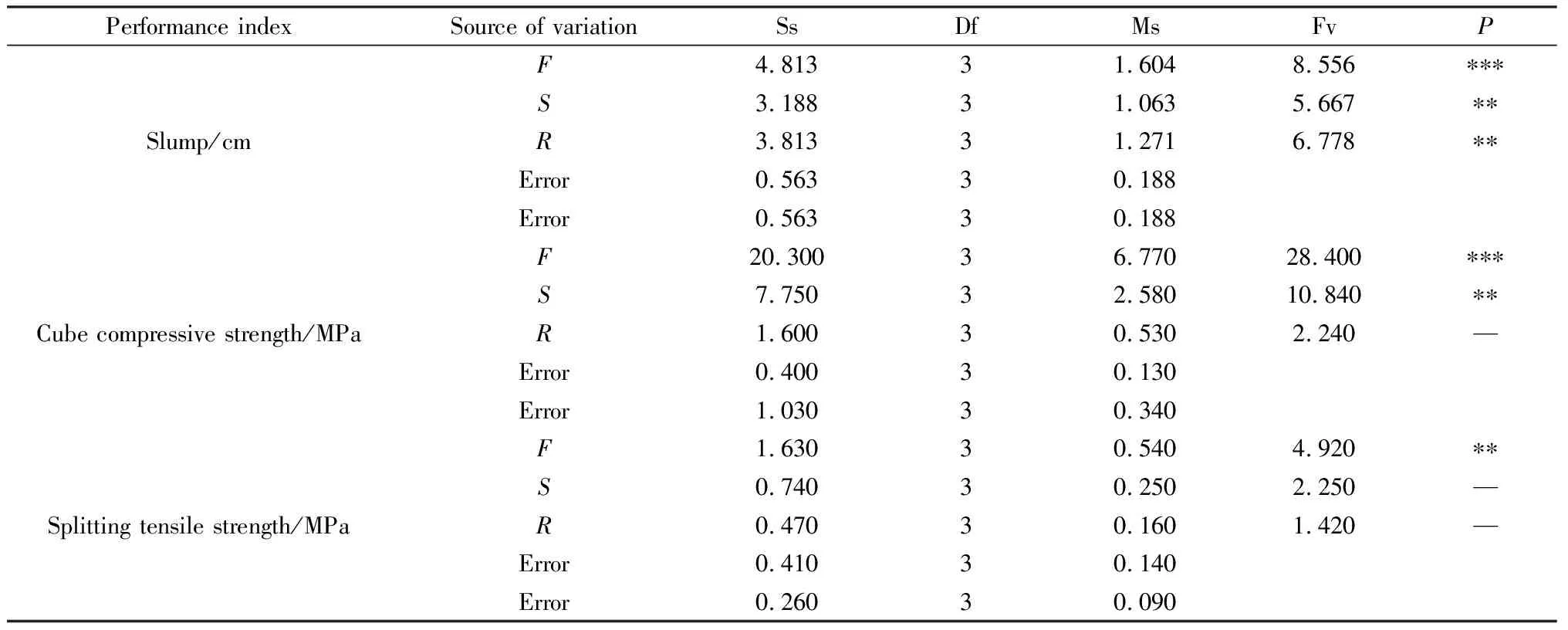
表8 粉煤灰-硅錳渣再生混凝土坍落度和強(qiáng)度方差分析檢驗(yàn)

2.2 三種材料對(duì)混凝土坍落度影響分析

由表7可以看出，三個(gè)因素對(duì)坍落度的影響程度由大到小依次為：F(1.375)=S(1.375)>R(1.250)。圖1為粉煤灰、硅錳渣、再生骨料三種固體廢棄物在不同取代量下對(duì)粉煤灰-硅錳渣再生混凝土坍落度影響的趨勢(shì)圖。

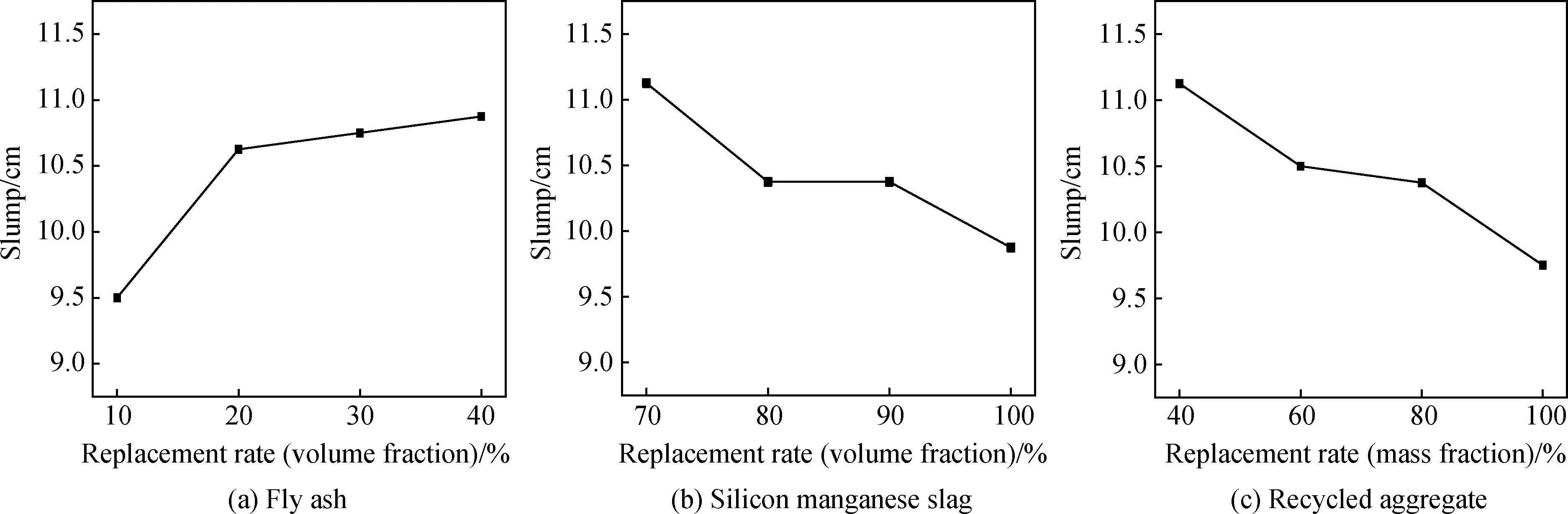
圖1 粉煤灰、硅錳渣、再生骨料不同取代率對(duì)混凝土坍落度的影響

由圖1(a)可知，隨著粉煤灰取代量的增加，混凝土坍落度增大，粉煤灰摻量由10%梯度遞增到40%時(shí)，坍落度分別增加了11.8%、13.2%、14.5%。結(jié)合混凝土坍落度發(fā)展規(guī)律與混凝土微觀樣貌圖分析，原因主要是粉煤灰顆粒多呈球形，表面光滑且具有較小的比表面積，這減少了顆粒的不規(guī)則性和顆粒間的摩擦，使膠凝材料黏附和覆蓋砂表面的能力較低，吸附水的能力也降低，從而增加了混凝土的和易性[9-10]。

由圖1(b)可知，硅錳渣對(duì)坍落度的影響呈負(fù)效應(yīng)，即硅錳渣取代砂量越高，混凝土坍落度越低，硅錳渣取代量由70%遞增到100%時(shí)，混凝土坍落度降低了11.2%，這是因?yàn)樗愫蟮墓桢i渣疏松多孔，較河砂空隙大，吸水率高，在混凝土初始拌和時(shí)會(huì)急速吸取加入的拌合水，間接降低水灰比，導(dǎo)致混凝土的坍落度降低。

由圖1(c)可知，再生骨料取代量由40%增加到100%時(shí)，混凝土坍落度降低了12.4%，原因是：(1)再生骨料是由廢舊混凝土機(jī)械破碎而得，破碎過(guò)程中會(huì)產(chǎn)生大量的棱角，也會(huì)使再生骨料內(nèi)部產(chǎn)生裂紋，將其用于混凝土?xí)r，再生骨料吸水率增大，混凝土坍落度降低；(2)再生骨料表面附著的舊砂漿以及孔隙會(huì)使混凝土吸水率增大，降低混凝土的坍落度[11-12]。

由表8可得，粉煤灰、硅錳渣、再生骨料取代量的Fv值均大于4.76，即三者對(duì)粉煤灰-硅錳渣再生混凝土的影響都是顯著的，顯著程度由大到小依次為：F>R>S。

2.3 三種材料對(duì)混凝土力學(xué)性能影響分析

2.3.1 立方體抗壓強(qiáng)度

由表7可以看出三個(gè)因素對(duì)混凝土立方體抗壓強(qiáng)度的影響程度由大到小依次為：F(2.890)>S(1.610)>R(0.740)。為更直觀地分析三種材料對(duì)混凝土立方體抗壓強(qiáng)度的影響，測(cè)得三種材料不同取代率下混凝土立方體抗壓強(qiáng)度變化曲線，如圖2所示。為更好地分析影響原因，還對(duì)混凝土試塊進(jìn)行了SEM表征和破壞形態(tài)圖分析，如圖3～圖5所示。

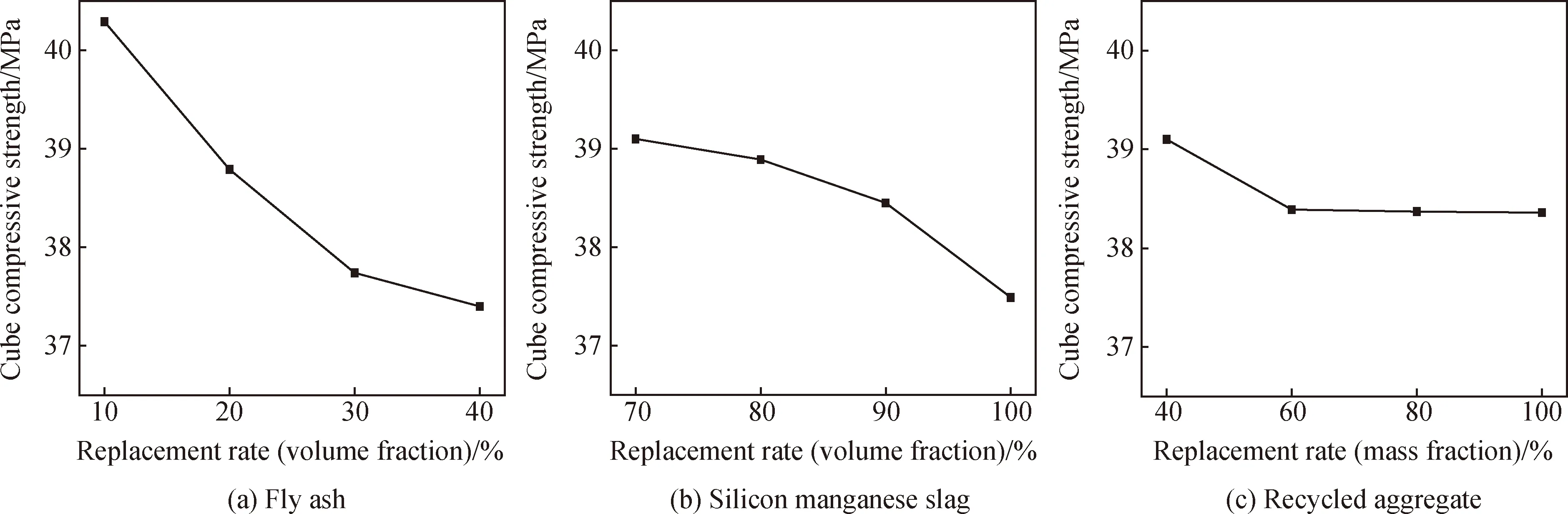
圖2 粉煤灰、硅錳渣、再生骨料不同取代率對(duì)混凝土立方體抗壓強(qiáng)度的影響

由圖2(a)可知，隨著粉煤灰摻量的增加，粉煤灰-硅錳渣再生混凝土立方體抗壓強(qiáng)度逐漸降低，粉煤灰取代量由10%梯度增加到40%時(shí)，立方體抗壓強(qiáng)度分別降低了3.7%、6.3%、7.2%，結(jié)合混凝土立方體抗壓強(qiáng)度發(fā)展規(guī)律與混凝土微觀樣貌圖分析,總結(jié)原因如下：(1)在水化初期，粉煤灰火山灰特性劣于水泥，粉煤灰的火山灰效應(yīng)并不明顯，此時(shí)主要是粉煤灰的微集料效應(yīng)，即通過(guò)填充作用對(duì)混凝土的強(qiáng)度做出貢獻(xiàn)，使混凝土強(qiáng)度低于正常水泥水化的混凝土強(qiáng)度[13]，從圖3也可以看出，混凝土內(nèi)部存在大量未水化的粉煤灰顆粒；(2)膠凝材料對(duì)混凝土強(qiáng)度的貢獻(xiàn)主要來(lái)于粉煤灰中的SiO2、Al2O3與水泥水化生成的Ca(OH)2進(jìn)行二次水化反應(yīng)后生成的C-S-H凝膠[14-15]，而當(dāng)混凝土處于28 d齡期時(shí)，粉煤灰的水化還未進(jìn)行完全，只生成部分C-S-H凝膠，導(dǎo)致混凝土的強(qiáng)度降低，且進(jìn)行二次水化反應(yīng)需要大量Ca(OH)2提供堿性環(huán)境，從時(shí)間上來(lái)說(shuō)，這也導(dǎo)致混凝土的強(qiáng)度發(fā)展有一定的 “滯后性”[16]。

圖3 粉煤灰-硅錳渣再生混凝土內(nèi)部SEM照片

由圖2(b)可知，硅錳渣取代量由70%梯度遞增到100%時(shí)，立方體抗壓強(qiáng)度分別降低了0.5%、1.7%、4.1%。原因?yàn)椋?1)硅錳渣粒徑級(jí)配分布沒(méi)有河砂級(jí)配良好，且從微觀樣貌圖可以看出硅錳渣周圍孔結(jié)構(gòu)松散，這導(dǎo)致混凝土結(jié)構(gòu)脆弱，且高孔隙率也使混凝土和易性變差，降低了混凝土的壓實(shí)度；(2)硅錳渣表面存在一些礦物成分，使表面與砂漿和再生骨料的黏結(jié)性變差，受壓時(shí)結(jié)構(gòu)發(fā)生急速破壞，導(dǎo)致強(qiáng)度降低。

由圖2(c)可知，再生骨料由40%梯度增加到100%時(shí)，立方體抗壓強(qiáng)度急速下降后呈趨平狀態(tài)，立方體抗壓強(qiáng)度分別降低了1.8%、1.9%、1.9%。原因?yàn)椋?1)再生骨料本身的強(qiáng)度取決于母體廢舊混凝土的強(qiáng)度，具有不統(tǒng)一性，且自身的高孔隙率、低壓碎值，以及再生骨料中含有的紅磚、砂漿塊等雜質(zhì)(圖4(a))都會(huì)降低混凝土的強(qiáng)度[17]；(2)再生骨料由天然骨料和砂漿組成，這導(dǎo)致其有三種界面過(guò)渡區(qū)(ITZ)，即天然骨料與舊砂漿之間(ITZ1)，天然骨料與新砂漿之間(ITZ2)，新舊砂漿之間(ITZ3)[18-19]，圖5為再生混凝土微觀樣貌圖，可以明顯看出界面過(guò)渡區(qū)的存在，其使再生骨料與天然骨料和砂漿的黏結(jié)力降低，混凝土受壓時(shí)會(huì)先沿界面過(guò)渡區(qū)產(chǎn)生裂縫(圖4(a))，在持續(xù)壓力影響下裂縫不斷延伸，最終導(dǎo)致混凝土破碎。

圖4 粉煤灰-硅錳渣再生混凝土不同力學(xué)性能的破壞形態(tài)圖

圖5 再生骨料界面過(guò)渡區(qū)SEM照片

顯著因素分析方面，由表8可以看出，粉煤灰、硅錳渣取代量的Fv值均大于4.76，即兩者是粉煤灰-硅錳渣再生混凝土立方體抗壓強(qiáng)度的顯著影響因素。由于粉煤灰取代量的Fv值(28.400)>硅錳渣取代量的Fv值(10.840)，粉煤灰取代量為立方體抗壓強(qiáng)度的高顯著影響因素，硅錳渣取代量為顯著影響因素，而再生骨料取代量為非顯著影響因素。

2.3.2 劈裂抗拉強(qiáng)度

由表7可以看出三個(gè)因素對(duì)混凝土劈裂抗拉強(qiáng)度的影響程度由大到小依次為：F(0.886)>S(0.542)>R(0.455)。圖6為三種材料不同取代率下混凝土劈裂抗拉強(qiáng)度變化曲線圖。

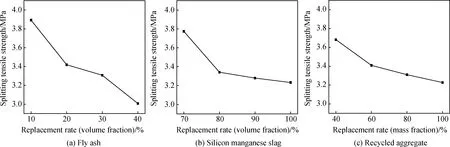
圖6 粉煤灰、硅錳渣、再生骨料不同取代率對(duì)混凝土劈裂抗拉強(qiáng)度的影響

由圖6(a)可知，粉煤灰-硅錳渣再生混凝土的劈裂抗拉強(qiáng)度隨著粉煤灰、硅錳渣、再生骨料取代量的增加而降低，粉煤灰取代量由10%梯度增加到40%時(shí)，劈裂抗拉強(qiáng)度分別降低了12.2%、15.0%、22.8%，摻量由20%增加到30%時(shí)，劈裂抗拉強(qiáng)度的降低幅度最小。

由圖6(b)可知，隨著硅錳渣取代量的增加，劈裂抗拉強(qiáng)度降低，較摻量70%的硅錳渣，摻量80%、90%、100%時(shí)，劈裂抗拉強(qiáng)度分別降低了11.5%、13.1%、14.4%。這主要是因?yàn)樯霸诨炷林衅鸬焦羌艿淖饔茫桢i渣取代砂時(shí)由于硅錳渣疏松多孔，當(dāng)受到集中應(yīng)力時(shí)易壓碎，混凝土內(nèi)部失去主要支撐，發(fā)生劈裂破壞。

由圖6(c)可知，再生骨料取代量由40%增加到60%、80%、100%時(shí)，劈裂抗拉強(qiáng)度分別降低了7.4%、10.1%、12.4%。原因主要為：(1)再生骨料母體混雜，本身強(qiáng)度較天然骨料低，從破壞形態(tài)圖的斷裂面可以看出大部分骨料都是直接斷裂(見(jiàn)圖4(b))；(2)再生骨料新舊砂漿結(jié)合處的過(guò)渡區(qū)使骨料間的黏結(jié)力差，造成粗骨料脫落(見(jiàn)圖4(b))，這是混凝土發(fā)生劈裂破壞的主要原因。

顯著因素分析方面，由表8可以看出，粉煤灰的取代量為混凝土劈裂抗拉強(qiáng)度的顯著影響因素，硅錳渣和再生骨料的取代量為非顯著影響因素。

3 NSGM(1，4)模型預(yù)測(cè)

NSGM(1，N)模型為曾波教授提出的一種新結(jié)構(gòu)多變量灰色預(yù)測(cè)模型，是對(duì)GM(1，N)(N表示用于建模的自變量和因變量個(gè)數(shù)之和)模型的優(yōu)化，可以更準(zhǔn)確地建立預(yù)測(cè)模型。

3.1 確定建模數(shù)據(jù)

選取前12組樣本數(shù)據(jù)構(gòu)建NSGM(1,4)模型，并用后4組數(shù)據(jù)進(jìn)行模型預(yù)測(cè)，檢驗(yàn)建立模型準(zhǔn)確性。選取立方體抗壓強(qiáng)度為系統(tǒng)特征數(shù)據(jù)系列X(0)1(因變量)。

X(0)1=(x(0)1(1),x(0)1(2),x(0)1(3)，…,x(0)1(12))=

(41.89,40.35,40.02,38.89,38.95,40.06,38.45,37.71,38.66,38.05,37.66,36.57)

(3)

式中：X(0)1中1表示第一組數(shù)據(jù)序列，(0)表示所涉及數(shù)據(jù)是未經(jīng)加工的原始數(shù)據(jù)。

粉煤灰、硅錳渣、再生骨料取代量為相關(guān)因素?cái)?shù)據(jù)系列X(0)i(i=2,3,4)(自變量)。

X(0)i=(x(0)i(1),x(0)i(2),x(0)i(3)，…,x(0)i(12)),(i=2,3,4)

(4)

式中：X(0)i中i表示影響因子的序號(hào)數(shù)。

帶入試驗(yàn)數(shù)據(jù)得

X(0)2=(0.1,0.1,0.1,0.1,0.2,0.2,0.2,0.2,0.3,0.3,0.3,0.3)

X(0)3=(0.7,0.8,0.9,1.0,0.7,0.8,0.9,1.0,0.7,0.8,0.9,1.0)

X(0)4=(0.4,0.6,0.8,1.0,0.6,0.4,1.0,0.8,0.8,1.0,0.4,0.6)

3.2 模型參數(shù)估計(jì)

(1)計(jì)算系統(tǒng)特征數(shù)據(jù)序列X(0)1和相關(guān)因素?cái)?shù)據(jù)序列X(0)2、X(0)3、X(0)4的一次累加生成序列X(1)1、X(1)2、X(1)3、X(1)4。

(5)

式中：X(1)j中j表示累加生成序列中不同影響因素的序號(hào)數(shù)，(1)表示進(jìn)行了一次累加運(yùn)算；k表示參與建模數(shù)據(jù)的序號(hào)數(shù)；g表示具體參與累加的數(shù)據(jù)組數(shù)序號(hào)。

帶入試驗(yàn)數(shù)據(jù)得

(2)計(jì)算系統(tǒng)特征數(shù)據(jù)序列X(1)1的緊鄰均值系列Z(1)1。

(6)

帶入試驗(yàn)數(shù)據(jù)可得

Z(1)1=(62.065,102.250,141.705,180.625,220.130,259.385,297.465,335.650,374.005,411.860,448.975)

(3)構(gòu)建參數(shù)矩陣B及Y，計(jì)算參數(shù)=(b2,b3,b4,a,h1,h2)T。其中b2,b3,b4,a,h1,h2為根據(jù)矩陣B和Y進(jìn)行求解所得，參數(shù)b的個(gè)數(shù)根據(jù)矩陣求解所得，a、h的個(gè)數(shù)為模型固定。

(7)

(8)

3.3 計(jì)算模型時(shí)間響應(yīng)式

(9)

式中：N為i的取值。

中間變量u1,u2,u3,u4：

(10)

計(jì)算帶入式(9)得

(11)

3.4 NSGM(1,4)模型模擬及預(yù)測(cè)誤差檢驗(yàn)結(jié)果

殘差：

(12)

式中：εs為殘差符號(hào)；k為樣本個(gè)數(shù)。

相對(duì)誤差：

(13)

式中：Δs為相對(duì)誤差符號(hào)。

平均相對(duì)誤差：

(14)

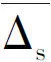
基于NSGM(1,4)的立方體抗壓強(qiáng)度模擬數(shù)據(jù)如表9所示，基于NSGM(1,4)的立方體抗壓強(qiáng)度預(yù)測(cè)數(shù)據(jù)如表10所示。

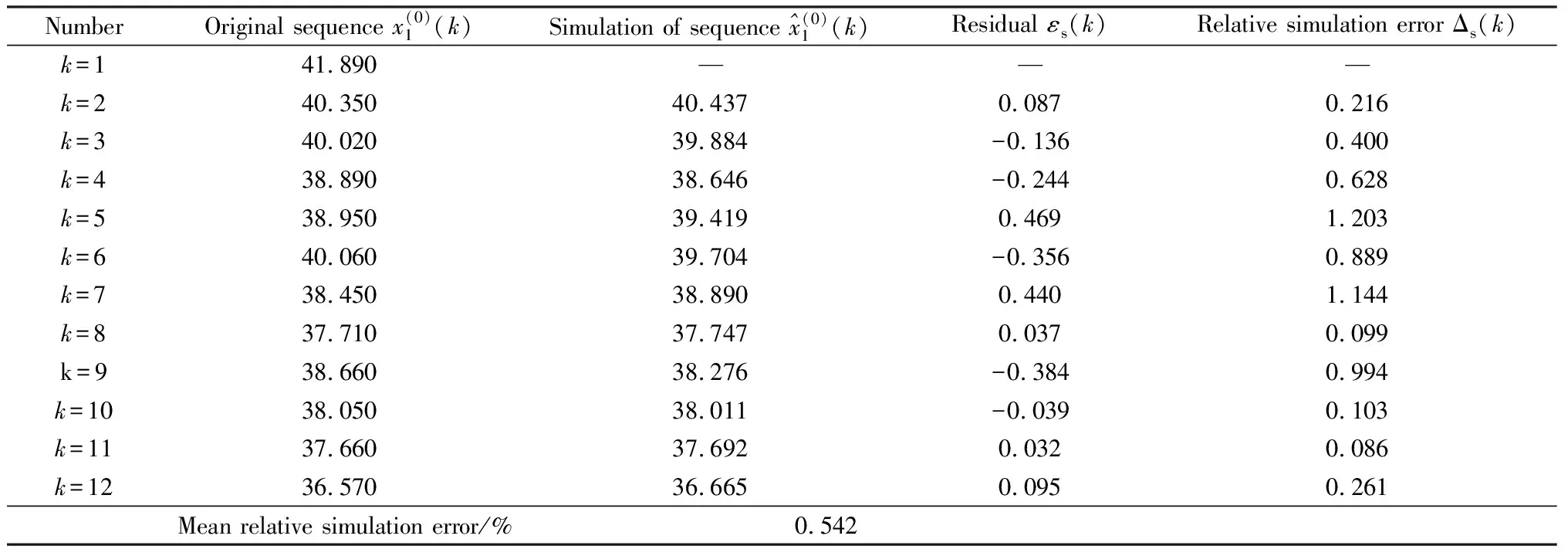
表9 基于NSGM(1,4)的立方體抗壓強(qiáng)度模擬數(shù)據(jù)

查閱灰色預(yù)測(cè)模型誤差等級(jí)參照表可知，NSGM(1,4)模型的誤差等級(jí)為Ⅰ級(jí)，表明模型具有較好的模擬性能，可用于不同粉煤灰、硅錳渣、再生骨料取代量下粉煤灰-硅錳渣再生混凝土立方體抗壓強(qiáng)度的預(yù)測(cè)。

通過(guò)表10可以看出，將NSGM(1,4)模型應(yīng)用于立方體抗壓強(qiáng)度預(yù)測(cè)時(shí)，預(yù)測(cè)誤差為2.727%，在Ⅱ級(jí)誤差內(nèi)，因此此模型可以應(yīng)用于實(shí)際工程中,對(duì)混凝土立方體抗壓強(qiáng)度做出預(yù)測(cè)。

表10 基于NSGM(1,4)的立方體抗壓強(qiáng)度預(yù)測(cè)數(shù)據(jù)

圖7為粉煤灰-硅錳渣再生混凝土立方體抗壓強(qiáng)度原始序列與模擬序列對(duì)比圖，前12組為立方體抗壓強(qiáng)度模型模擬數(shù)據(jù)值，后4組為模型預(yù)測(cè)值，可以看出模擬序列與原始序列近似程度高，模型有較好的模擬預(yù)測(cè)效果。

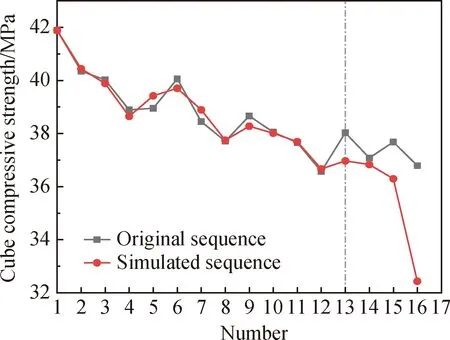
圖7 粉煤灰-硅錳渣再生混凝土立方體抗壓強(qiáng)度原始序列與模擬序列對(duì)比圖

4 結(jié) 論

(1)粉煤灰摻量的增加會(huì)提高粉煤灰-硅錳渣再生混凝土的坍落度，降低混凝土的立方體抗壓強(qiáng)度和劈裂抗拉強(qiáng)度，立方體抗壓強(qiáng)度最大降幅為7.2%，劈裂抗拉強(qiáng)度最大降幅為22.8%。

(2)硅錳渣和再生骨料摻量的增加均會(huì)降低粉煤灰-硅錳渣再生混凝土的坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度。摻加硅錳渣時(shí)，混凝土立方體抗壓強(qiáng)度和劈裂抗拉強(qiáng)度的最大降幅分別為4.1%、14.4%；再生骨料對(duì)混凝土抗壓強(qiáng)度影響較小，最大降低率為1.9%，劈裂抗拉強(qiáng)度最大降低率為12.4%。

(3)粉煤灰為坍落度、立方體抗壓強(qiáng)度、劈裂抗拉強(qiáng)度的顯著影響因素，硅錳渣為坍落度和立方體抗壓強(qiáng)度的顯著影響因素，再生骨料為不顯著影響因素。

(4)通過(guò)NSGM(1,4)模型可以實(shí)現(xiàn)粉煤灰、硅錳渣、再生骨料取代量對(duì)混凝土立方體抗壓強(qiáng)度和劈裂抗拉強(qiáng)度的模擬和預(yù)測(cè)，模型模擬平均相對(duì)誤差為0.542%，模型預(yù)測(cè)平均相對(duì)誤差為2.727%。