第34屆中國化學奧林匹克競賽試題解法賞析
——以試題1-2為例

昆明學院化學化工學院（650214）張 吉 楊艷華 王建坤 李艷妮

云南迪慶藏族自治州民族中學（674499）楊春香

云南紅河州瀘西縣白水鎮初級中學（652404）朱薇麗

歷經30 多年的中國化學奧林匹克競賽已逐漸成為全國重要的知識性競賽項目，這項賽事不僅為中學生提供了一個了解現代化學科研和科技前沿信息的渠道，還為全國高校選拔優秀化學后備人才提供了參考。通過初賽和決賽選拔，優秀選手可代表中國登上國際舞臺，為國爭光。

第34 屆中國化學奧林匹克競賽（初賽）于2020年9 月12 日舉行，全國有約7 萬名高中生參加。本次初賽試題的命題核心思想依然是引導學生在夯實基礎知識、掌握正確方法的基礎上開拓思維和不斷思考，試題結合實際、注重前沿［1］。本次初賽試題出現了一道獨立計算題，即試題1-2［2］，為近些年少有的變化內容之一。下面筆者對該計算題的解法進行剖析，希望能為學生提供一些化學計算題解題思路，使更多的學生體會到探索的樂趣。

一、試題與參考答案

【試題1-2】現有鋁鎂合金樣品一份，稱取2.56 g樣品溶于HCl，產生2.80 L H2（101.325 kPa，0 ℃），通過計算，確定此合金組成。

【參考答案】［3］鋁、鎂均可以和鹽酸反應生成氫氣，2.80 L 氫氣一部分由鋁與鹽酸反應生成，另一部分由鎂與鹽酸反應產生。根據Mg、Al 與HCl 的反應方程式：Mg+2HCl＝MgCl2+H2↑，2Al+6HCl＝2AlCl3+3H2↑，可以得出反應中Mg、Al 與H2的物質的量的關系分別是Mg →H2、Al →1.5 H2，即n(Mg) mol 的鎂與鹽酸完全反應產生n(Mg) mol 的H2，而n(Al) mol 的鋁與鹽酸完全反應產生1.5n(Al) mol的H2。

解得：x=52.7%，1-x=47.3%。

則鋁的質量分數為52.7%，鎂的質量分數為47.3%。

二、其他解題方法

現在的教育注重鍛煉學生的思維能力，讓學生學會從多個方面去思考問題，靈活地運用不同的方法解決問題。針對該題，除中國化學會官網公布的解法外，筆者還從差量法、守恒法、假設法、十字交叉法、平衡計算等中學化學計算題常用解題方法中探尋出以下幾種解題思路。

（一）守恒法

守恒法主要包括質量守恒法、物質的量守恒法、物料守恒法、質子守恒法、能量守恒法、離子守恒法、電子守恒法和電荷守恒法等。根據本題給出的條件，可選用物質的量守恒法、質量守恒法和電子守恒法進行計算求解。

思路一：物質的量守恒法

解：設合金中Mg和Al的物質的量分別是xmol和ymol。

根據Mg、Al與HCl的反應可以得出：

反應所得氫氣的物質的量為：

思路二：質量守恒法

解：設合金中Mg的質量為xg，Al的質量為yg。

上述兩種解題方法雖然運用的思路不同，但都是質量守恒和物質的量守恒相結合，列出二元一次方程進行求解。

思路三：電子守恒法

Mg、Al 與HCl 反應生成H2是置換反應，屬于氧化還原反應范疇，反應過程中涉及電子得失，因此可用電子守恒法進行求解。

解：設合金中Mg和Al的物質的量分別是xmol和ymol。

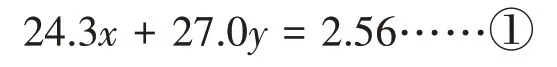
Mg、Al 與HCl 的反應屬于氧化還原反應，由此可得合金中金屬失去的電子數=氫氣得到的電子數。

根據Mg、Al與HCl的反應可以得出：Mg →H2↑，2Al →3H2↑。

根據還原反應方程式可得：

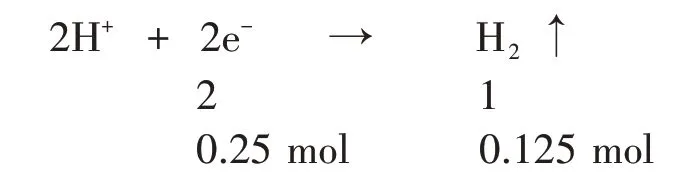
H+得到0.25 mol 電子，而這0.25 mol 電子正是兩種金屬失去電子的總和。

根據氧化反應方程式可得：

可以看出，xmol 的Mg 和ymol 的Al 完全被氧化需要失去(2x+3y) mol電子。

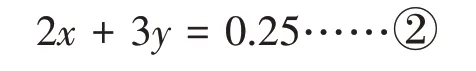
由①②兩式聯立可得：x=0.05 mol，y=0.05 mol

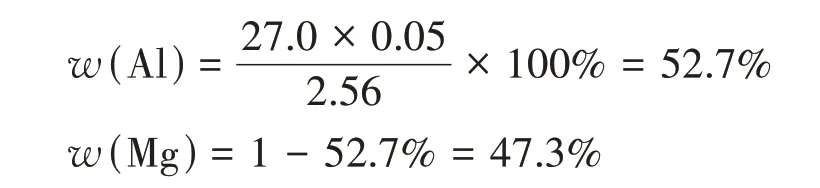
（二）十字交叉法

由于合金中Mg、Al 的質量百分含量總和為1，且合金與鹽酸反應生成的H2總體積介于與合金等質量的兩種金屬分別與鹽酸反應產生的氫氣的體積之間，因此可以運用十字交叉法進行計算求解［4］。

解：設Al的質量為m，則Mg的質量為2.56-m。

根據Mg、Al 與HCl 的反應方程式，可以得出反應中Mg、Al 與H2的物質的量的關系為Mg →H2、Al →1.5H2。

假設合金全為Mg，根據關系式可得：

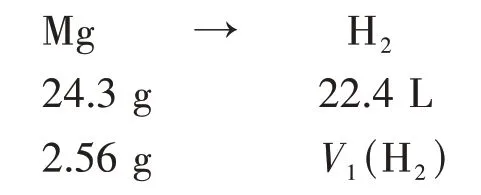
由此可以計算出Mg 完全反應產生的氫氣的體積：

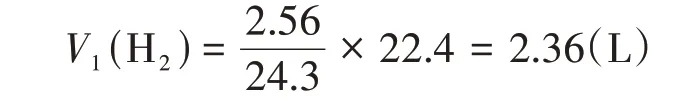
假設合金全為Al，根據關系式可得：

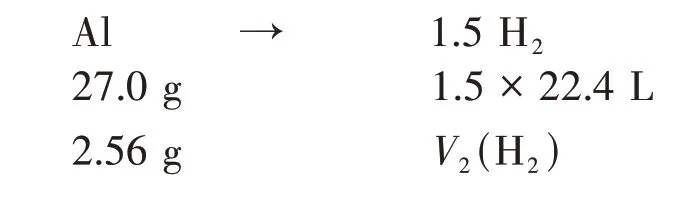
由此可以計算出Al 完全反應產生的氫氣的體積：

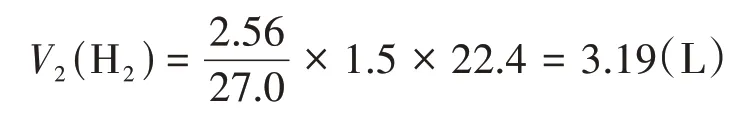
由十字交叉法得：

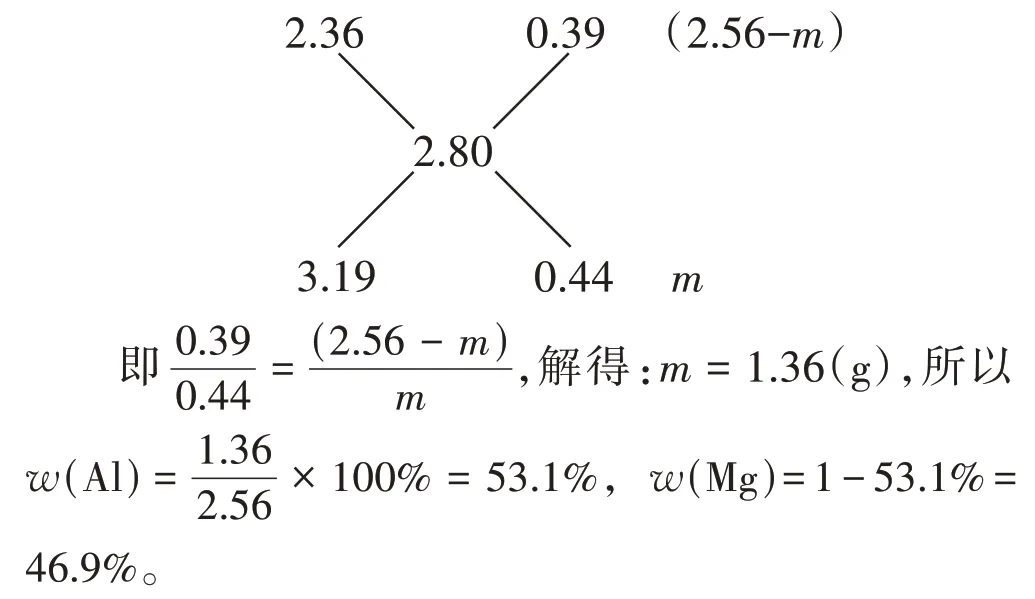
經過上述幾種解題思路的推演，我們發現，用不同的方法計算出的答案有一定的偏差。在參考答案中也做了補充說明，即因采用的相對原子質量不同而導致結果的最后一位數字稍有差別，可以正常得分。但為什么我們采用了與參考答案一致的相對原子質量，有的計算結果還是與參考答案有偏差？造成這一結果的原因可能是對應保留的有效數字未做明確要求。因為題目中并未說明計算結果應該保留幾位有效數字，所以在計算過程中只能按個人習慣保留相應的有效數字，從而造成計算結果的偏差。

因此在解答計算題時，應該抱著嚴謹求實的態度，全面地考慮問題，盡可能地把偏差降到最低。同時，這也提醒命題者命題時應力求表述清晰、嚴謹、精確，即使考生從不同的角度去理解和分析題目，最后都能得到統一的答案。

三、總結與反思

計算題是中學化學各類考試的必考題型之一，其注重考查學生對圖表、數據和信息的綜合分析能力，體現了以“三維（知識內容、思想方法、認知能力）學習理論”為命題基礎的化學學科核心素養考試［5］。在解答試題1-2 這樣的計算題時，應注意以下兩點。

（1）充分認識化學反應的本質。只有牢牢抓住化學反應前后的“變”與“不變”，才能真正地理解化學反應過程中的“守恒”。掌握物質間相互轉化的守恒關系，可使問題的內在關系以更加清晰簡潔的方式呈現出來，進而簡化解題過程。

（2）十字交叉法是解決二組分混合物中組分比例關系的常用方法。正確選擇混合物中的兩個分量和平均量，明確兩個量之比及量值代表的物理意義，進而運用二元一次方程進行求解。

無論是基于化學反應的本質進行計算，還是運用數學思維進行解答，守恒法和十字交叉法在解決有關二組分混合物的計算問題時有著殊途同歸的作用。通過對試題1-2 解題思路的研究，不僅可以開拓學生思維，還可以啟迪教師在教學中要提高學生透過現象看本質的意識和分析與解決問題的能力，培養學生“變化觀念與平衡思想”化學學科核心素養。