例談法向量在立體幾何中的應用

江蘇省清江中學（223001）趙麗云

空間向量與立體幾何是高中數學的重點內容，也是高考的必考知識點。空間向量法在立體幾何中的應用，從某個角度看，就是法向量在空間幾何中的應用。空間向量法可大大減少幾何思維量，但增加了運算量。所謂平面的法向量，就是垂直于平面的空間向量。法向量是破解各類立體幾何問題的有效工具，它不僅可以幫助解題者判斷或證明空間基本圖形的位置關系，還可以幫助解題者計算空間距離和空間角以及解決立體幾何探索性問題。

一、利用法向量證明線面平行、面面平行

將立體幾何置于空間直角坐標系中，可以通過平面向量的坐標運算來證明空間平行關系，包括線面平行和線線平行。線面平行，只需證明直線的方向向量與平面的法向量垂直，而證明面面平行，則只需證明它們的法向量互相平行。

［例1］已知正方體ABCD-A1B1C1D1的棱長為2，E、F分別是BB1，DD1的中點，求證：（1）FC1∥平面ADE；（2）平面ADE ∥平面B1C1F。

證明：如圖1所示建立空間直角坐標系D-xyz，則有D(0,0,0），A(2,0,0)，C(0,2,0)，C1(0,2,2)，E(2,2,1)，F(0,0,1)，所以

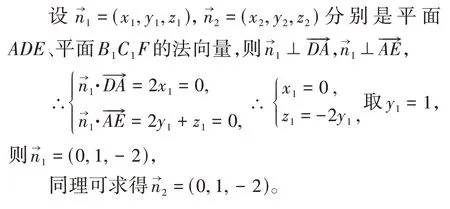
點評：無論是證明線面平行，還是面面平行，關鍵是找到相關平面的法向量。當建立空間直角坐標系后，一般可采用方程思想求出法向量的坐標，通過坐標運算來證明或驗證平行關系。

二、利用法向量證明線面垂直、面面垂直

將立體幾何置于空間直角坐標系中，同樣可以利用空間向量的坐標運算證明垂直關系。要證線面垂直，只需證明直線的方向向量與平面的法向量平行；而要證面面垂直，則只需證明它們的法向量互相垂直。

［例2］已知正方體ABCD-A1B1C1D1中，E是BB1的中點，F是CD的中點。

求證：（1）D1F⊥平面ADE；（2）平面A1D1F⊥平面ADE。

證明：（1）如圖2 所示建立空間直角坐標系D-xyz，令AA1=2，則D(0,0,0)，D1(0,0,2)，A(2,0,0)，E(2,2,1)，F(0,1,0)，

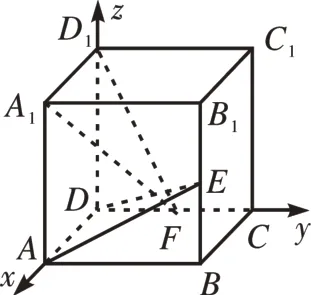
圖2

點評：利用法向量證明垂直關系與利用法向量證明平行關系“驚人相似”，解答的關鍵是利用坐標法求出相關平面法向量的坐標，進而通過平面向量數量積坐標運算加以驗證。

三、利用法向量求線面夾角、面面夾角

將立體幾何置于空間直角坐標系中，處理斜線與平面所成的角，只需先求出斜線和這個平面的法向量的夾角，因為這個角和直線與平面所成的角互余，所以很容易求出斜線與平面所成的角；而對于二面角的平面角的求解，通常可先求出它們的法向量的夾角，因為這個夾角或者它的補角就是所要求的二面角的平面角，具體取舍哪個，要看圖形而定。

［例3］已知正方體ABCD-A1B1C1D1中的棱長為2，

（1）求直線AD與平面A1BC1所成的角的正弦值；

（2）求平面A1B1C1D1與平面A1BC1所成的二面角（銳角）的余弦值。

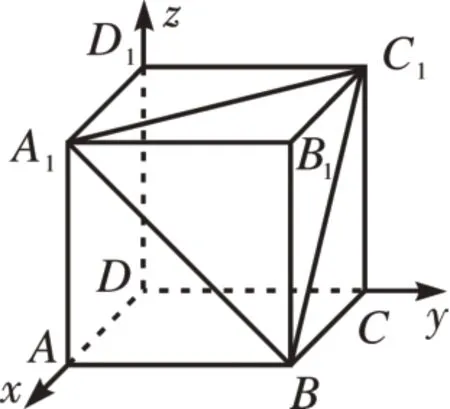
圖3

點評：空間角是有范圍的，當它表示特殊角時可用反三角函數來表示。本例第（2）問已經注明所求的二面角是銳角，否則它也可能是而線面角與線線角都不可能是鈍角，尤其是求線線角時，若利用法向量計算的角的余弦值為負，則應轉負為正。

四、利用法向量求空間距離

在立體幾何中空間距離有點面之距、線面之距、面面之距等。將立體幾何置于空間直角坐標系中，空間距離同樣可以利用空間向量的坐標來求得，但必須先求出該平面的法向量的坐標。求點面之距，可先求經過這點的某斜線段的長m，再求該斜線與平面的法向量所成的角θ，于是所求距離d=msinθ；而面面之距與線面之距都可轉化為點面之距來求得。對于兩異面直線之間的距離，可先求它們的公共法向量，再在兩條直線上分別各取一點，那么過這兩點的向量在法向量上的射影的長度即為所求。

［例4］如圖4的正方體ABCD-A1B1C1D1中，

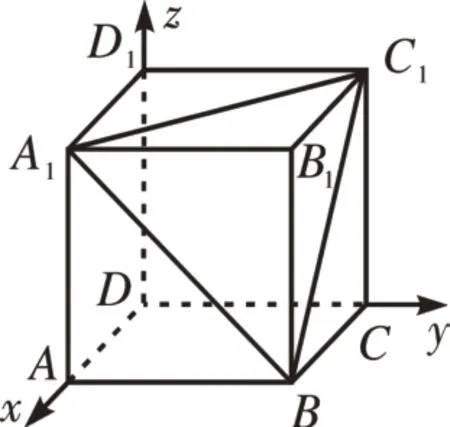
圖4

（1）求點B1到平面A1BC1的距離；

（2）求A1B與B1C之間的距離。

解析：（1）由例3 知=(1,1,1)是平面A1BC1的一個法向量，設點B1到平面A1BC1的距離為d，則

設A1B與B1C1間的距離為d，則

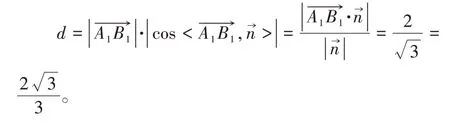
點評：利用法向量求空間距離，通常將其轉化為求直角三角形的一條直角邊長來處理，因此可利用坐標法求出該直角三角形的斜邊和法向量與該斜邊所在的向量的夾角的余弦值。

五、利用法向量求解立體幾何探索性問題

立體幾何的探索性問題，通常要求解題者在動態中探求符合要求的空間元素的位置。平面的法向量的方向雖然是固定的，但它是自由向量，在求解立體幾何的探索性問題時引入法向量，能夠幫助解題者快速解決問題。

［例5］如圖5，在直三棱柱ABC-A1B1C1中，已知側面AA1B1B是正方形，AB=BC=2，E，F分別為AC和CC1的中點，D是棱A1B1上 的 點，且 滿 足BF⊥A1B1。問當B1D為何值時，面BB1C1C與面DFE所成的二面角的正弦值最小？

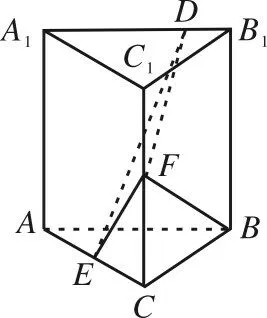
圖5

解析：∵三棱柱ABC-A1B1C1是直三棱柱，∴BB1⊥底面ABC，∴BB1⊥AB。∵A1B1∥AB，BF⊥A1B1，∴BF⊥AB，又BB1?BF=B，∴AB⊥平面BCC1B1，∴BA,BC,BB1兩兩垂直。以B為坐標原點，分別以BA,BC,BB1所在直線為x,y,z軸建立空間直角坐標系，如圖6，∴B(0,0,0)，A(2,0,0)，C(0,2,0)，B1(0,0,2)，A1(2,0,2)，C1(0,2,2)，E(1,1,0)，F(0,2,1)。由題設D(a,0,2)（0 ≤a≤2）。

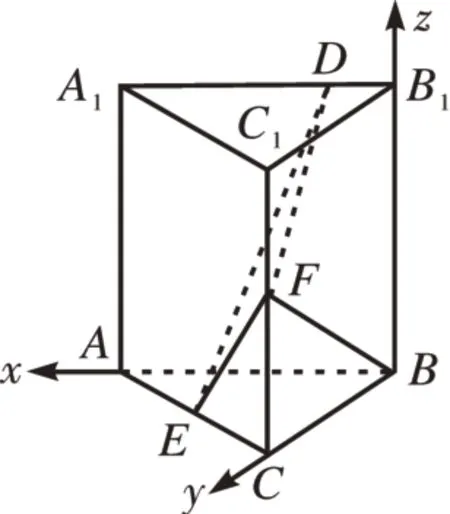
圖6

令z=2 -a，則m→=(3,1 +a,2 -a)，∵平 面BCC1B1的法向量為=(2,0,0)，設平面BCC1B1與平面DEF的二面角的平面角為θ，

點評：本題主要考查空間向量的相關計算，在求解時，利用法向量的特征建立二面角余弦的函數關系，從而求得二面角的余弦值的最大值，進而找到正弦值最小值，由此求出B1D的長度。

由此可見，坐標化的立體幾何為法向量的應用開辟了廣闊的道路，讓法向量有了“用武之地”。法向量除了可以解決以上四類問題，還可以解決立體幾何的探索性問題，這里限于篇幅，不再詳細闡述。值得一提的是，無論是利用法向量解決立體幾何中的哪種問題，關鍵是準確無誤地求出法向量的坐標，把原問題坐標化，將幾何問題轉化為代數問題。