HPM融入導數教學的研究

江蘇蘇州市吳縣中學（215000）江佳慧

一、研究的目的和意義

第一，學習導數能夠豐富學生解決問題的方法，鍛煉學生思考問題的能力。

在解答導數相關問題時，學生需要靈活運用各種解題方法，全面掌握導數的所有知識點。在學習導數時，學生要轉變原有的數學觀，從不變到變化、從有限到無限、從靜態到動態、從常量到變量。

第二，微積分中包含極限思想、函數思想和數形結合思想等。在高中階段教授微積分可以鍛煉學生的探索意識和思維能力，提高學生解決問題的能力。

研究我國教育史可以發現，數學教學內容有限，發展十分緩慢。起初只教授算術，之后才在中學教材中逐步添加幾何、代數、數列和不等式等內容，微積分這一部分知識在很長一段時間里都沒有被添加到高中教材中，高考也未涉及，只有一些學有余力的、有興趣、有天賦的學生把微積分作為數學學科競賽的參考資料去學習。這主要是因為部分研究學者認為，微積分中的思想方法對于高中生來說是難以接受的，提早讓他們接觸這一部分內容會讓他們心有余而力不足，逐漸失去探究解決數學問題的興趣。但是，隨著我國義務教育的全面普及，學生學習能力的提高，學習資源與學習環境的逐步優化，導數作為微積分的一部分基礎知識被納入教學大綱，成為高中數學選修教材內容中的一部分，目的是做好高中數學導數與高等數學微積分的銜接，鍛煉學生探索的意識，提高學生探究問題和解決問題的積極性，優化學生解決問題的方法。

第三，從數學文化價值看，可讓學生通過自主探索數學的歷史發展過程，體會數學的文化內涵，激發學生的民族自豪感。

培養什么人，是教育的首要問題［1］。把立德樹人作為學校的立身之本，是時代的要求。

微積分的基礎內容導數被寫進了高中數學教材，高中生首次接觸到新的領域，面對新的數學思想和數學方法，肯定會對它的來歷和作用產生疑惑，它是怎么來的？有什么用處？在我國古代，劉徽提出割圓術：“割之彌細，所失彌少，割之又割，以至于不可割，則與圓周合體而無所失矣。”［2］其中涉及的分割思想、極限思想等都是微積分的雛形。雖然微積分的雛形在我國古代早已出現，但由于我國自古以來都是農業生產國，數學發展進程相比西方較慢。

了解數學史，一方面可以提升學生的民族自豪感、自信心，另一方面可以鼓勵學生學好數學，增強學生的愛國主義精神。數學教師不能單純地教授課本知識，要在課本知識的基礎上，延伸數學思想，拓展傳播數學文化。

筆者基于HPM 設計高中微積分教學，將數學史和數學問題貫穿整個教學活動，引導學生自主探索、主動學習。

二、導數的概念教學設計

環節一：數學史情境引入

導入：17 世紀，牛頓熱衷于研究物體的運動規律，他遇到這樣一個運動：一輛馬車向前跑，路程s和時間t滿足s=t2。

分析：馬車1 s走完1 m，2 s走完4 m，3 s走完9 m，速度越來越快，顯然是做變速運動，在牛頓之前研究物體的運動規律的數學家能夠算出一段時間內的平均速度，例如從第5 秒到第6 秒，小車從25 m處走到36 m處，這段路程的平均速度但牛頓并不滿足于算平均速度，他更想知道既然是變速運動，那么速度是如何變化的，也就是每一個時刻的瞬時速度。

問題1：小車在第5秒的瞬時速度是多少？

分析：第5秒經過的時間為0，經過的路程還是0。牛頓將問題看成動態的，從平均速度的原理出發，逐步縮短時間間隔，計算第5 秒到第5.5 秒的平均 速 度：

問題2：10.5仍是平均速度，這么做有什么意義？

分析：雖然10.5 也不是瞬時速度，但是因為時間間隔縮短了，10.5比11更接近第5秒時的瞬時速度，所以只要不斷縮短時間間隔，求出平均速度，就會無限接近第5 秒時的瞬時速度，這就是微積分思想的雛形——無限接近思想。利用這個想法，牛頓最終求出瞬時速度。

活動：計算并觀察。

隨著時間間隔的縮短，平均速度越來越接近10 m/s。

理論依據：從第5 秒開始，取一個特別小的時間間隔Δt，第5 秒到第(5+Δt)秒這段時間的平均速度因為Δt是一個特別小的數，所以可以將其舍去。

設計意圖：引用數學史，激發學生探索的興趣。引導學生感受牛頓用計算平均速度的方式推導出計算瞬時速度的過程，理解無限接近思想。

環節二：以數學史引出極限概念

情境引入：牛頓的想法公布后，數學家貝克萊指出了其中的問題：將Δt當成一個非常小的量，但不是0，將其放在分母位置，約分后算到(10+Δt)時將其看作0 舍去，但如果Δt不是0，那么就不能舍去；如果是0，則怎么能放在分母位置？這一問題的提出，引發了第二次數學危機。這個問題目前還沒有得到完美解決，但不斷縮小時間間隔，用平均速度逼近瞬時速度，即為微積分思想的雛形。數學家是如何填補牛頓邏輯上的漏洞的呢？

問題3：牛頓最后算出(10+Δt)，直接舍去Δt，得到瞬時速度為10。

活動：列出下列表格。

分析：事實上，并不是舍去Δt，也不是令Δt等于0，而是讓(10+Δt)中的Δt不斷接近0，然后考慮(10+Δt)會如何變化。(10+Δt)不斷靠近10，離10越來越近，隨著Δt不斷趨近于0 而無限接近于10時的就是瞬時速度。由此引出了一個重要概念——極限。什么是極限？簡單來講就是，觀察一組數的變化過程，看它會不斷趨近于哪個數，最終趨近的那個數就叫作這個變化過程的極限。在上述例子中，我們就可以說，當Δt趨近于0 時，(10+Δt)的極限等于10。

問題4：什么是趨近？多近才叫趨近？當Δt趨近于0 時，(10+Δt)確實會不斷接近10，但它也會不斷接近9.9，為什么說極限是10，而不是9.9呢？

設計意圖：通過引入貝克萊指出牛頓想法中的問題這一情境，啟發學生思考，讓學生用矛盾與發展的眼光看問題，讓學生感受到數學創造的曲折性和嚴謹性，以及數學是不能模棱兩可地解釋的。

環節三：認識極限

情境引入：法國數學家達朗貝爾認為，一個變量趨近于一個固定量，趨近的程度小于給定的任何正數，那么這個固定量就叫作這個變量的極限。這個想法道出了極限的精髓，首先極限主要研究變量的變化趨勢；其次極限的判斷標準為變量和極限的差小于任何給定的正數。

問題5：這個數列有沒有極限？

實際上，無論這個正數ε 怎么給，我們都可以在數列里找到某一項，從它開始，后面的數與0的差都小于這個定值。

為什么當Δt趨近于0 時，(10+Δt)的極限是10，而不是其他的數，比如9.9呢？

變量(10+Δt)與定值10 之間趨近的程度，即|Δt|，Δt可以小于任意給定的正數，因為Δt→0，因此我們可以說(10+Δt)的極限是10。為什么不是9.9 呢？因為(10+Δt) 與9.9的趨近程度為|Δt+0.1|，Δt→0，|Δt+0.1 |始終大于等于0.1，不小于任何給定的正數，所以(10+Δt)的極限不是9.9。

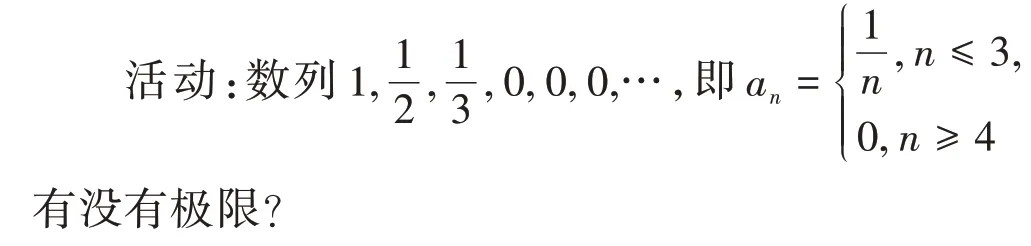
環節四：換個角度看瞬時速度

問題6：為什么瞬時速度就是平均速度的極限呢？

分析：路程s和時間t滿足s=t2，求t=5秒時的瞬時速度。

我們從第5 秒開始，取一個時間間隔Δt，算出第5 秒到第(5+Δt)秒這一段時間的平均速度==10+Δt，Δt趨近于0 時，平均速度(10+Δt)的極限10就是瞬時速度。

我們換一個角度，看看還能如何通過平均速度得到瞬時速度。在滿足s=t2的運動中，小車的速度會越來越快，做加速運動，t=5 秒時的瞬時速度v要小于其他時刻的瞬時速度，v一定小于這段時間內的平均速度(10+Δt)，v＜(10+Δt)。因此，無論時間間隔多么小，瞬時速度v都小于平均速度(10 +Δt)，即這個式子對任意Δt ＞0恒成立。

活動：列表觀察。

得出結論：v≤10。為什么可以等于10 呢？因為Δt＞0，所以(10+Δt)取不到10。因此，v可以取10，而這個10就是我們前面所說的極限。

問題7：這也只能說明v ＜10，怎么能說明v=10呢？

分析：剛才是取第5 秒后的時間段，下面我們來取第5 秒前的時間段(5 -Δt)s～5 s，再重復一遍剛才的過程。

環節五：引出導數概念

引出問題8：假設位移隨時間變化，位移和時間是兩個變量，滿足s=t2，兩個變量滿足一定的對應關系，根據函數的概念，用函數表示為f(x)=x2，前面我們了解到瞬時速度是平均速度的極限，那么平均速度和瞬時速度的抽象含義是什么呢？

問題8分析：平均速度的抽象含義。（如下表）

平均速度的抽象含義就是函數的平均變化率，它表現了函數在[5,5+Δx]上平均變化的趨勢。

活動：計算任意一點x=x0處的瞬時變化率。

瞬時速度的抽象含義即讓Δx→0，函數在[5,5+Δx]的變化會無限趨近于定值10。f(x)=x2在x=5 處的變化趨勢，也叫作x=5 處的瞬時變化率，換句話說，對于函數f(x)=x2，我們可以用牛頓的方法計算出x=5處的瞬時變化率：

總結：計算函數瞬時變化率的方法。

函數：y=f(x)；

固定自變量：x=x0，增量Δx；

函數值：f(x0)，f(x0+Δx)；

函數值的變化量：Δy=f(x0+Δx) -f(x0)。

當Δx趨近于0 時趨近于定值l，l叫作函數y=f(x)在點x=x0處的瞬時變化率。為了方便使用，數學家給函數f(x)在點x=x0處的瞬時變化率起了新名字，叫作函數f(x)在點x=x0處的導數，用符號f′(x0)表示。