基于Logistic 回歸模型的航材外站配放策略

■ 闞士行 王崢/山東航空股份有限公司工程技術公司

0 引言

航空公司航線網絡具有點多、面廣、線長的特征。為保障航線網絡的暢通，航空公司需要在主基地之外的航站配放一定量的過站常用航材。目前，大部分航空公司采用歷史經驗數據決定某一航站是否配放航材，決策過程缺少數據定量分析支撐，存在標準不一、經濟性低的情況。本文以SC 航空公司外站配放航材為例，通過建立Logistic 回歸模型，為外站航材配放提供決策數據支撐，并通過ROC 曲線選定最優閾值，評估模型的優劣。

1 模型簡介

1.1 Logistic 回歸模型

針對連續型因變量，可以應用線性回歸對因變量進行解釋或預測。但對離散型因變量，尤其是二分類因變量，只有“行”與“不行”、“0”與“1”的區別，這時就要應用Logistic 回歸進行分析。

對線性回歸表達式y=wTx，y的取值為（-∞，∞），但想獲得的是一個在[0，1]之間的值。因此，需要一個轉換函數將y值轉換成[0，1]之間的值。這個函數稱為Logistic函數，又稱為Sigmoid函數，如圖1 所示。

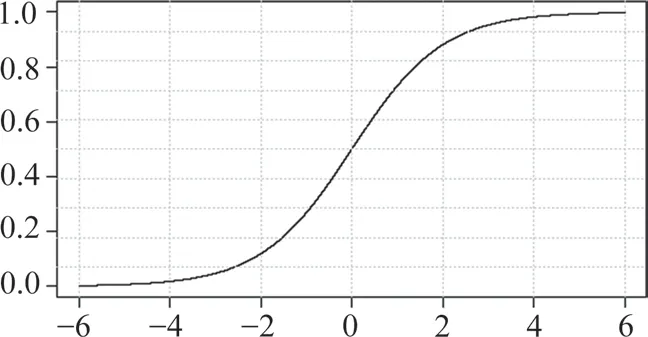
圖1 Sigmoid函數

構造Sigmoid 函數為

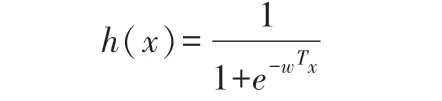
式中，對分類結果分別為1 和0 的概率為

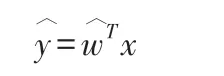
一般設定閾值為0.5，即

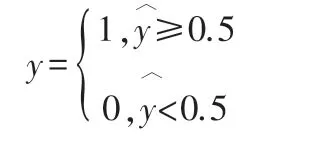
1.2 ROC 曲線

ROC 曲 線（Receiver Operating Characteristic Curve）又稱為受試者工作特征曲線。簡單來講，對一個二分問題，即實際分為正類（Positive）和負類（Negative），針對該實例進行預測，會有4 種結果，如表1 所示。

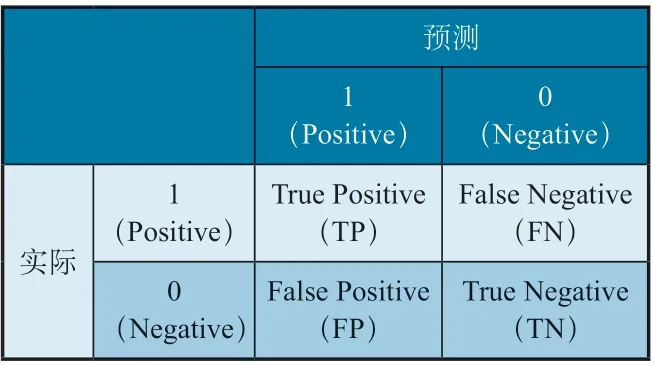
表1 二分問題混淆矩陣

定義

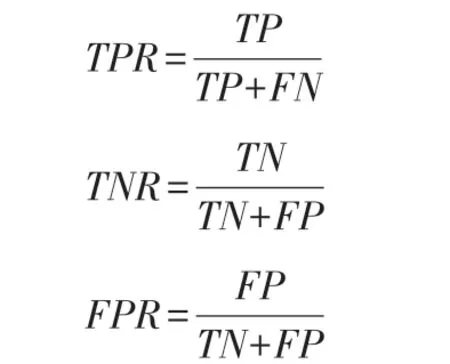
其中，TPR（靈敏度，sensitivity）為在所有實際為1（Positive）的樣本中，將其正確地判斷為1（Positive）的比率；TNR（特異度，Specificity）為在所有實際為0（Negative）的樣本中，將其正確地判斷為0（Negative）的比率；FPR（1-Specificity）為在所有實際為0（Negative）的樣本中，將其錯誤地判斷為1（Positive）的比率。

如果一種預測方法能夠使TPR 變高、FPR 變低，那么這種方法能夠有效區分樣本。但這兩個指標相互制約。若某方法比較敏感，稍有指征即判斷為1（Positive），則TPR 會很高，但同時也會將很多實際為0（Negative）的誤判為1（Positive），即FPR 會很高。在最極端的情形下，所有樣本都判斷為1（Positive），那么TPR 值為1，FPR 的值也為1。

根據不同的閾值，將大于該閾值的判斷為1（Positive），小于該閾值的判斷為0（Negative），則會得到相應的（FPR，TPR）值，將其描繪在坐標軸中，得到相應的ROC 曲線。可見，ROC 曲線是一個很好的分類器。

圖2 是一個ROC 曲線的例子，圖中黑色曲線為ROC 曲線，淺藍色區域的面積 為AUC（Aera Under Curve）。AUC為衡量分類器優劣的一個指標。一般來講，若AUC 為0.5，即圖中正方形對角線（灰色直線），則該分類器沒有預測價值，等同于隨機猜測；AUC 越大越好，一般在0.8 左右，該分類器即有較大的應用價值。使AUC 最大的閾值，是所需要的。

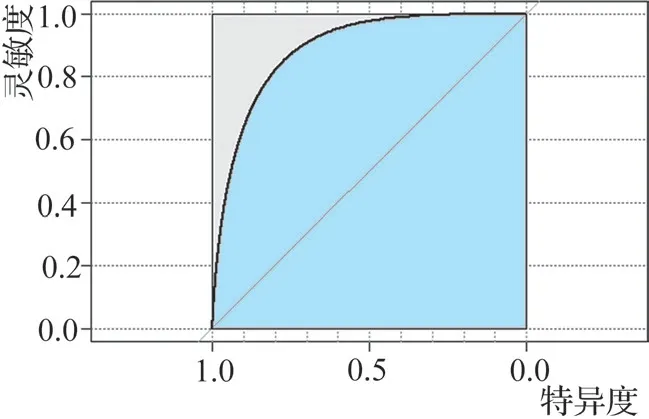
圖2 ROC曲線

2 模型應用

2.1 Logistic 模型的建立

以本文為例，因變量為二分類變量，

自變量包含4 個參數，分別為SC公司過去1 年在該航站的航班量（X1）、該航站距離最近基地航司的距離（X2）、SC 公司在該航站歷史上是否發生過故障（X3）以及該航站其他航司相應資源數量（X4），其中X3樣為二分類變量。

對SC 公司69 個航站收集數據如表2 所示。

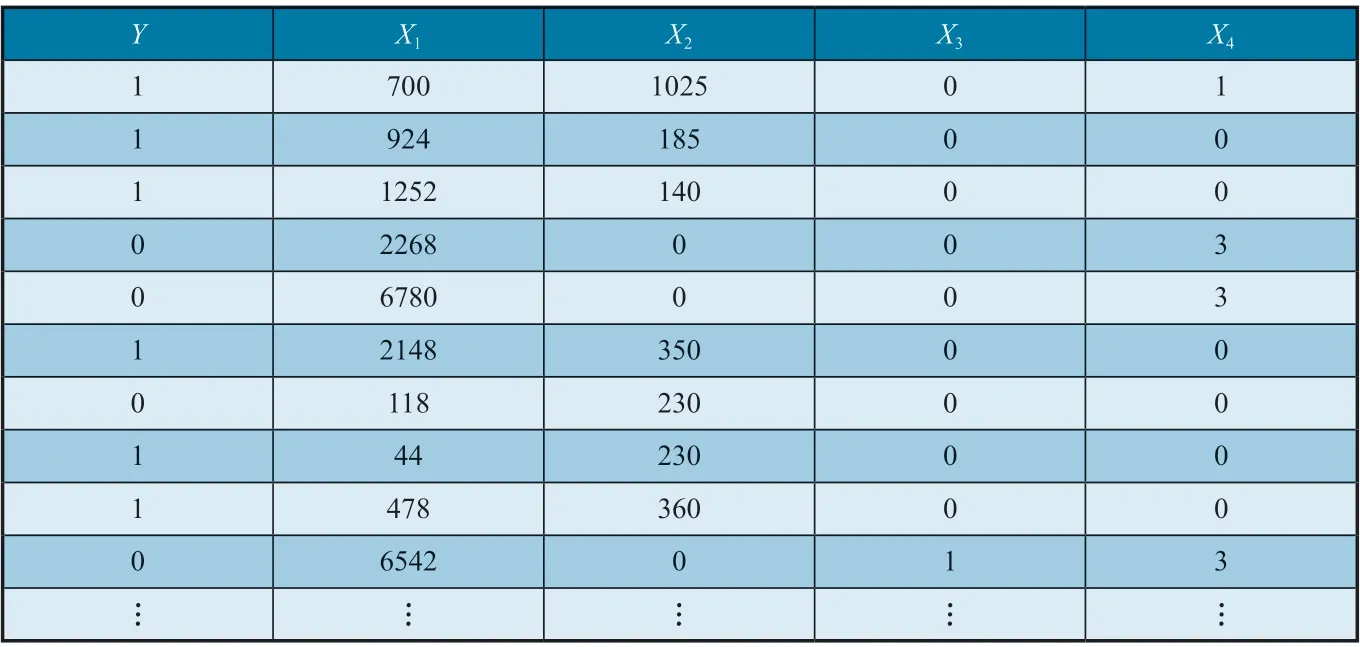
表2 SC公司航站數據

通過R 語言應用Logistic 回歸，得到如表3 所示的結果。

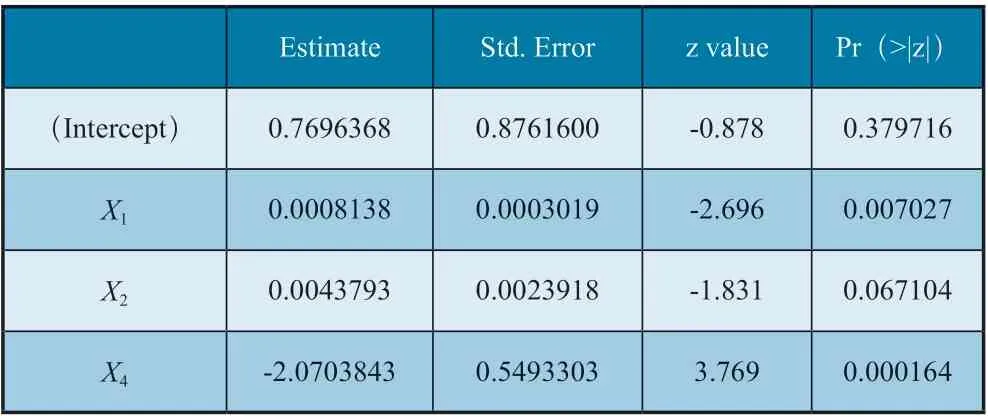
表3 Logistic回歸結果

X2的P 值稍大于0.05，結果不顯著。但若將X2剔除后重新進行Logistic 回歸，得到如表4 所示的結果。

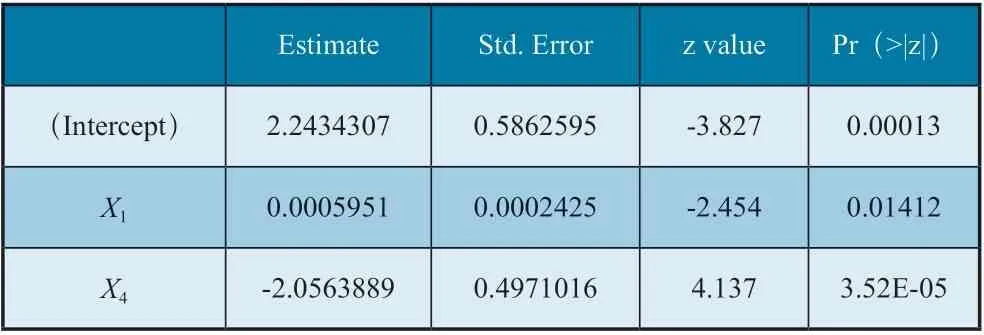
表4 將X2剔除后的Logistic回歸結果

包含X1、X2與X4三個自變量的Logistic 模型的AIC（赤池信息量）為56.11；包含X1、X4兩個自變量的Logistic 模型的AIC（赤池信息量）為59.76。從AIC 看，應當選擇包含X1、X2與X4三個自變量的Logistic 模型。

綜合考慮，認為包含X1、X2與X4三個自變量的Logistic模型較為合理。最終Logistic 模型公式為

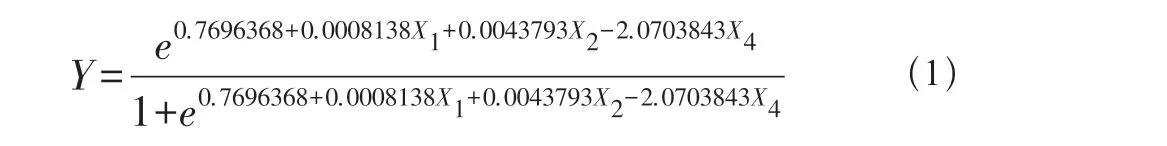
2.2 ROC 曲線的應用

根據公式（1），利用R 語言做出ROC 曲線，如圖3 所示。使得AUC 最大的閾值為0.76，即Y值大于0.76 的，預測為1（positive），否則預測為0（Negative）。

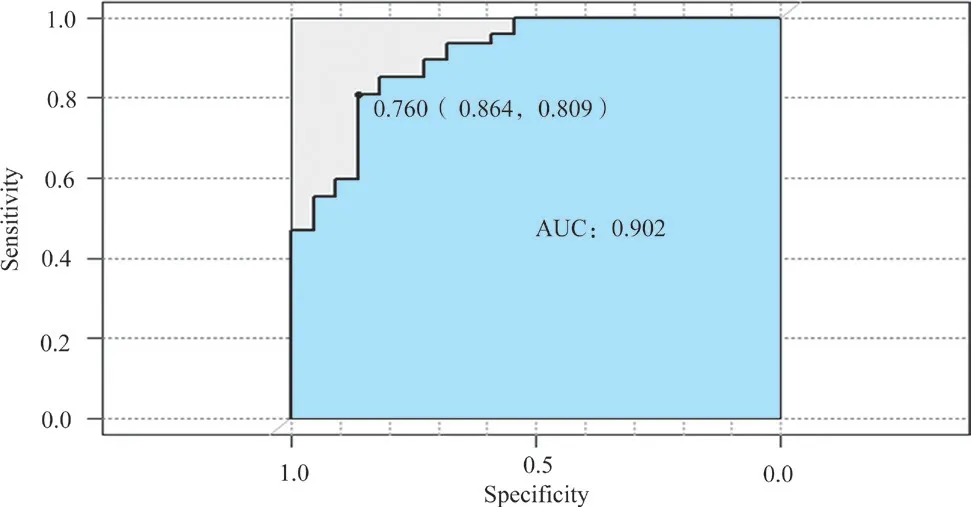
圖3 模型應用得到的ROC曲線

當閾值為0.76 時，針對原始數據應用回歸模型測算混淆矩陣如表5 所示。

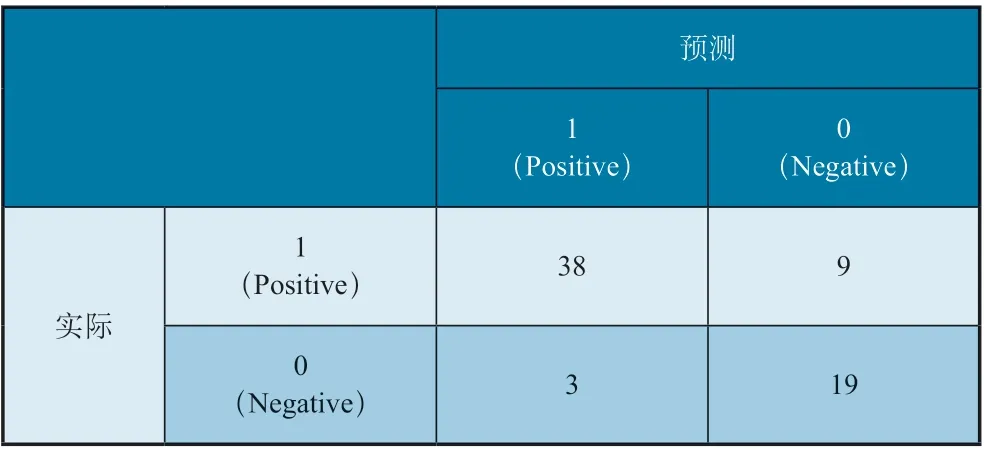
表5 預測結果混淆矩陣

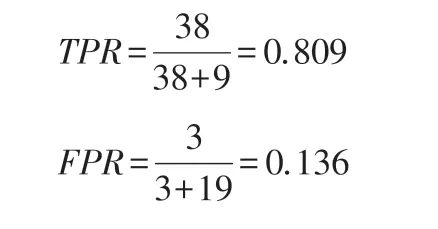
此時，AUC 為0.902，區分度較好，此閾值下ROC 曲線為一個較好的分類器。同時，若按照預測結果進行配放，則能節約13%的配置成本。假設SC 公司外站配置航材總成本為200 萬元，可通過該模型減少26 萬元的航材配置。

若選用包含X1、X4兩個自變量的Logistic 模型測算AUC，其AUC 僅為0.695，此時閾值為0.6。此閾值下ROC曲線的AUC 僅稍高于0.5，分類效果較差。

2.3 應用案例

若某新開飛航站預計未來一年航班量為360 班次，與最近的基地航司距離為500km，該航站其他航司資源數量為0，計算得到的Logistic 模型的概率為0.96，大于閾值0.76，則應在當地配放航材。

3 總結

本文通過以上分析建立了較好的分類模型，可為后續在外站是否配放航材提供了定量的數據支持，便于施行統一的航材外站配放標準，節約航空公司外站配放成本。