基于時間序列模型的上證A股指數實證分析

宋雅晴，康晴晴，劉 兮

(合肥師范學院 數學與統計學院，合肥 230601)

自滬深兩市交易所1990年開市之后，規模日益擴大，上市公司數量與日俱增，A股市場機制不斷健全與完善，成為重要的資本市場。2019年科創板規則正式落地，為創新驅動打開了空間，股市發展進入了一個新階段。股市中的某些規律性隱匿于市場內部，對股價歷史軌跡形態的描繪與演繹，可為未來價格趨勢預測提供重要線索，因而構建精準的模型兼具理論與實際意義。鑒于此，豐富完善股票指數內容，創新股價指數預測方法，能夠使投資者、政府決策者、企業決策者準確地把握股市波動的規律性，在瞬息萬變的股市中做出明智選擇。

1 文獻綜述

20世紀80年代起，國外學者將時間序列分析研究視野轉向了多變量、異方差、非線性場合，有效補充了ARIMA模型的不足。Black(1976)發現股價波動的杠桿效應，即利空消息與利好消息對波動的影響是非對稱的[1]；Bollerslev(1986)提出了GARCH模型，刻畫了金融市場風險的變化過程[2]；Nelson(1991)等提出了TARCH和EGARCH兩個非對稱模型[3]。近年來，鑒于中國股市的特殊性，國內學者提出了多種股市走勢分析方法。劉紅梅(2008)對鞍鋼股份建立了ARIMA模型，進行了短期分析[4]；吳朝陽(2010)利用改進的灰色模型與ARMA模型進行股指預測[5]；郭海櫻(2010)基于ARCH模型實證分析了上證A股指數收益率的波動情況[6]；符一平(2015)等利用ARCH簇模型對上證綜指進行實證研究，得出上證綜指具有明顯的尖峰厚尾性、波動聚簇性、信息不對稱性[7]。鐘立新(2020)等基于GARCH-MIDAS模型分析了政策因素對股市波動長期成分的影響[8]。基于此，對2017-2021年的上證A股指數進行時間序列分析，篩選出最優模型，為加強我國股市的合理性提出一些建議。

2 模型簡介

2.1 Box-Jenkins模型——ARIMA模型

Box-Jenkins方法利用外推機制描述時間序列，能達到最小方差意義下的最優預測。ARIMA(p,d,q)模型結構如下：

(1)

其中，p表示自回歸階數，d表示差分階數，q表示移動平均過程的階數，{et}為零均值白噪聲序列，?d=(1-B)d,Φ(B)=1-φ1B-…-φPBP是p階自回歸系數多項式，Θ(B)=1-θ1B-…-θqBq是q階移動平均系數多項式。

2.2 GARCH簇模型

Bollerslov基于ARCH理論，提出GARCH模型，增加了對異方差函數p階自相關性的考慮，可擬合具有長期記憶性的異方差函數；為提高預測精度，可采用GARCH的衍生模型。具體模型有以下幾種形式：

①GARCH模型：

(2)

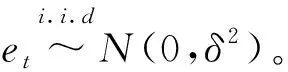
②AR-GARCH模型：

(3)

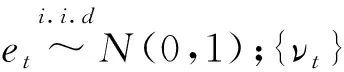
③EGARCH模型：

(4)

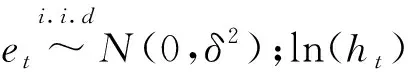
④GARCH-M模型：

(5)

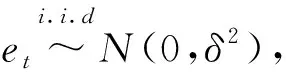
2.3 水平——波動綜合模型

鑒于全面性考慮，采用ARIMA模型與GARCH簇模型分別提取序列水平與波動信息，既可對序列未來水平進行預測，又可繪制波動置信區間圖，完成對序列更完整的認識。

3 實證分析

3.1 選取數據

為了確保科學性和實效性，以2017年3月20日-2021年3月19日的上證A股指數收盤數據為樣本數據，預測時間為2021年3月22日-26日；通過與真實數據對比，評價預測精度，選出最佳模型。

3.2 數據預處理

第一，原始序列平穩性檢驗。為了判斷數據的平穩性，首先進行單位根檢驗如表1所示，ADF檢驗統計量為-2.11，P=0.24>0.05，即具有非平穩性。因此，為了消減序列波動，對原序列作一階差分運算。

表1 上證A股ADF檢驗結果表Tab.1 Shanghai A shares ADF test results

第二，差分序列性質考察。對差分序列進行ADF檢驗，結果表明差分序列具有平穩性；由圖1、圖2可知，偏自相關系數具有明顯拖尾性；同時通過對差分序列進行白噪聲檢驗，得到P值小于0.05，即為非白噪聲序列。因此，在下一步建模中，應分別提取水平和波動信息。

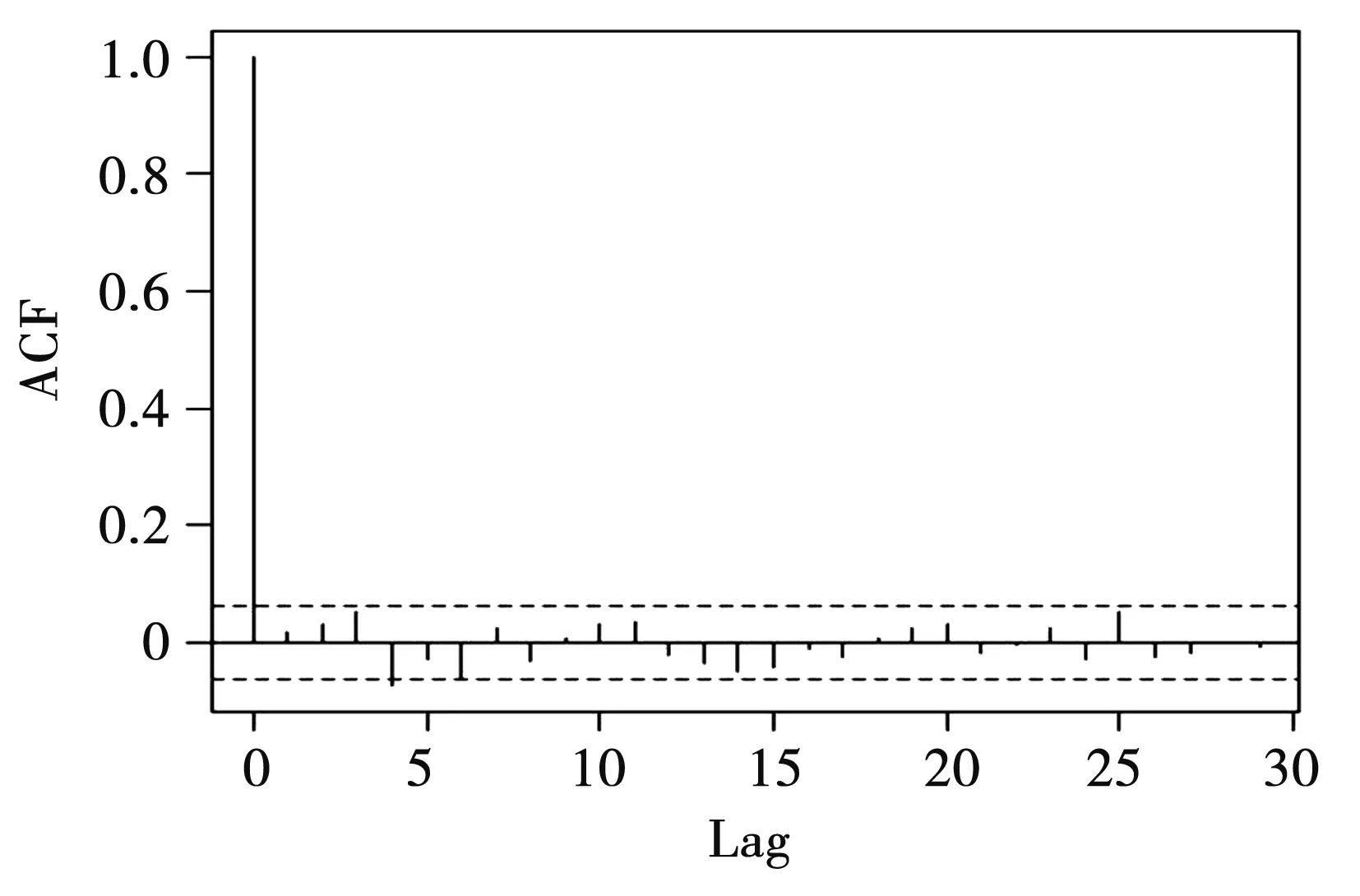
圖1 差分序列自相關圖Fig.1 Autocorrelation diagram of difference sequence

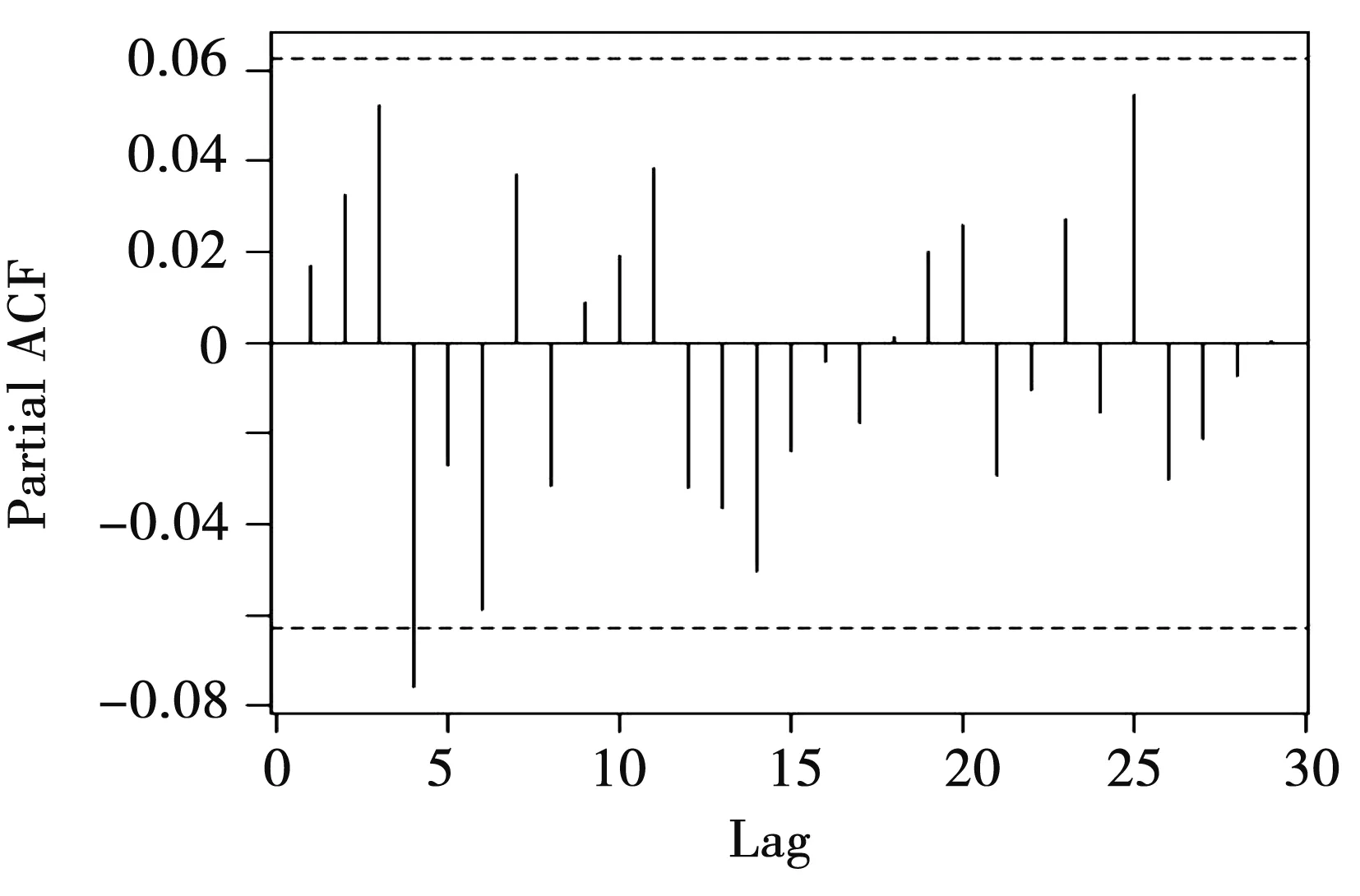
圖2 差分序列偏自相關圖Fig.2 Partial autocorrelation diagram of difference sequence

3.3 建模分析

第一，水平信息提取。通過對比分析與模型識辯，建立最終模型為ARMA(2，1，2)，表達式如下：

xt=0.375 1xt-1-0.892 2xt-2+et+0.374 3et-1-0.932 7et-2

(1)

殘差白噪聲檢驗顯示，P=0.66>0.05，即殘差序列具有隨機性，且各參數通過檢驗，模型顯著有效。運用ARIMA(2，1，2)模型，估計出2021年3月22日-26日共5個交易日的收盤價如表2所示。

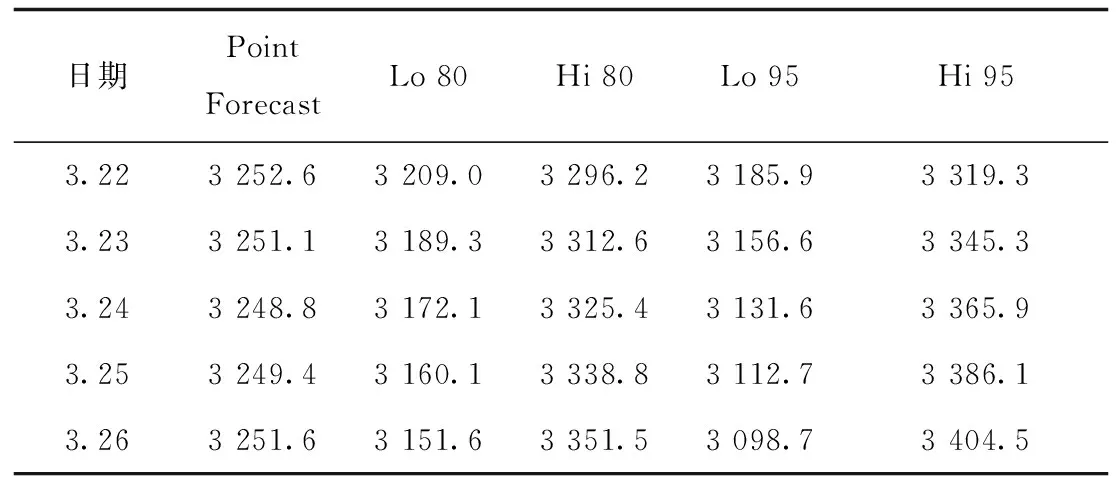
表2 上證A股收盤價預測表Tab.2 Closing price forecast of Shanghai A shares

比較ARIMA(2，1，2)模型的預測值與真實值，發現相對誤差均很小，且真實值基本都落在95%預測區間之內，說明該模型精度較高、預測效果良好，能夠用來預測上證A股指數的走勢。

第二，波動信息提取。為了檢驗模型的殘差是否具有ARCH效應，進行異方差檢驗，根據LM檢驗，可知χ2=31.199，P=0.002<0.05，即殘差序列呈現出異方差、長期相關的特征。擬合GARCH模型，經過調試得到EARCH(1，1)模型中參數對應的P<0.05，說明模型擬合效果較好。為了進一步檢驗序列的“杠桿效應”，擬合非對稱的EGARCH模型，模型中參數均顯著，存在杠桿性。通過對比分析可知，EGARCH(1，1)擬合效果最優。如表3所示。

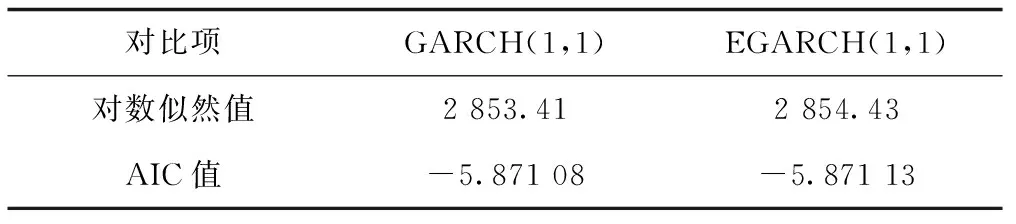
表3 GARCH(1，1)與EGARCH(1，1)模型檢驗比較表Tab.3 Comparison of GARCH(1，1) and EGARCH(1，1) model

EGARCH模型為：

(2)

在各種lag值下，F統計量對應的P<0.05，模型無ARCH效應，擬合效果良好。根據以上分析，可以得出最優模型——ARIMA-EGARCH模型如下：

(3)

4 結論與建議

以上證A股指數為對象，建立了ARIMA模型和GARCH簇模型，評價分析預測結果，最終篩選出最優模型。得出結論：上證A股指數的波動具有持續性、非平穩性的特點，差分序列具有平穩性；ARMA(2，1，2)模型殘差序列存在異方差性，具有ARCH效應，EGARCH(1，1)模型擬合效果最優。為了加強我國股市的效用性與合理性，規避股市風險，提出以下建議：國家應完善法律法規，規范股市運營手段，真正實現依法治“股”；政府應建立健全股市機制，轉變職能地位間接調控股市；企業應合理優化資源配置，加強自身創新能力與競爭力；投資者應加強對股市的洞察力，提高自身防御風險的能力。