差分隱私軟大間隔聚類

謝云軒

(南京航空航天大學，江蘇 南京 210000)

如今，AI技術幾乎在每個行業都顯示出其獨特的優勢。優勢之一便來自大數據驅動。雖然對大數據的挖掘用于研究與決策可極大地改善社會體系，但是數據的共享同時也伴隨隱私的泄露。因此必須保護那些提供個人身份信息等各種機密數據的用戶的隱私。比如當研究機構使用這些信息進行模型訓練并將模型公開時，隱私信息可能會泄露。因此，有必要在模型訓練過程中增加隱私保護技術。

在數據挖掘的眾多方法中聚類(Clustering)是一種較流行的無監督學習手段，其將數據集劃分為多個由相似示例組成的簇，使得同一簇內的任何兩個示例的相似性大于不同一簇的任意兩個示例的相似性。然而，對于大規模數據或分布式存儲數據，一般的單機聚類算法無法滿足對其聚類的訓練需求，即使可行，訓練的時間代價也過于高昂。因此，對單機聚類算法進行分布式改造，減少對大規模數據或分布式存儲數據訓練的時間成本，是提高其伸縮性的有效途徑。

在分布式計算中，不同節點通過在迭代更新中解決本地子問題并上傳解，從而求得全局閉式解，達到整個模型的收斂。但是，不同節點的通信過程會帶來隱私泄露的風險。因此，在迭代通信中，需要引入隱私保護技術確保隱私沒有泄露的風險。

因而近年隱私保護理念持續受到人們的關注，其在數據挖掘、機器學習和深度學習等許多領域都得到廣泛的應用。其中差分隱私通過混淆查詢響應來防止對手獲得關于隱私數據的信息，可以為個體隱私提供嚴格的保證而得到廣泛研究。具體而言，差分隱私將隨機噪聲加入待通訊的數據，從而避免攻擊者執行攻擊來推測數據集的若干敏感信息。

盡管學界已提出了極其豐碩的高性能聚類算法，比如DeepClustering等，但對大量現有聚類算法不做選擇地改造并不實際。因此本文將隱私保護改造局限于相對簡單但又有代表性的聚類算法，目的不是提出新的單機聚類算法，而是示范如何讓相對簡單但又有代表性的聚類算法適應聯邦學習環境，使之發揮更大的潛能。

軟大間隔聚類(Soft Large Margin Clustering, SLMC)性能相對認可又簡單，直接將數據映射到預定的個輸出標記實現聚類。除了不同于FCM(Fuzzy C-Means)在數據空間內的聚類之外，其作為判別型算法在標記空間進行聚類產生的良好性能和一定程度的可解釋性，并受到后續關注。因此本文選擇將其進行隱私保護優化。當面對潛在的隱私泄露風險時，分布式軟大間隔聚類(Distributed Sparse SLMC, DS-SLMC)與其他分布式聚類算法一樣，遭遇了類似的瓶頸。因此引入隱私保護改造是一個自然選擇。然而，改造的挑戰是如何在保持原有聚類算法收斂速度和準確度的同時，降低隱私泄露的風險。需要對改造后的算法進行理論證明，看其是否符合差分隱私準則，并利用實驗進行驗證。

本文為了提高SLMC的隱私保護能力，發展出差分隱私軟大間隔聚類(Differentially Private SLMC, DP-SLMC)。具體來說，在DS-SLMC迭代的過程中加入隨機高斯噪聲，為個體隱私提供嚴格的保證。同時通過-zCDP給出嚴格的隱私分析，證明本文提出的模型滿足差分隱私準則。

本文的具體貢獻如下：

1)將軟大間隔聚類與聯邦學習進行結合，通過引入隨機高斯噪聲減少不同節點間通訊導致隱私泄露的風險，從而解決不同節點進行分布式機器學習中的隱私問題。

2) 我們通過(,)-DP與-zCDP之間的關系進行理論證明，得到DP-SLMC算法的隱私保證。確保DP-SLMC算法滿足差分隱私準則。

3) 利用數據集進行了廣泛的實驗并對其非隱私版本進行比較，證明所提出算法的有效性。

1 相關工作

1.1 差分隱私

差分隱私定義如定義1-3所述。

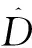
(1)

其中Z()的上界為的可能性至少為1-。

(敏感度) 查詢函數()對輸入的敏感度為：

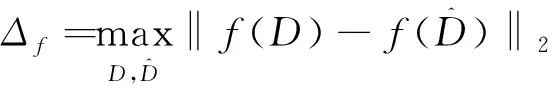
(2)

(高斯機制).對于函數而言, 高斯機制A定義為：

(,,)=()+

(3)

其中為從N(0,)的高斯分布中采樣的噪聲。高斯機制需要將其加入函數的輸出中。當滿足式(4)時，高斯機制A滿足(,)-DP。

(4)

零集中差分隱私(zero concentrated differential privacy,-zCDP)是一個差分隱私的松弛版本，利用Rényi散度來度量隨機函數在相鄰數據集上的分布差異。-zCDP 如定義4所述。

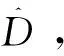
下文的引理1-3顯示了-zCDP 與(,)-DP 的關系以及-zCDP的合成定理.

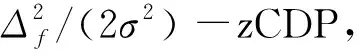
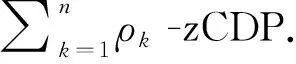
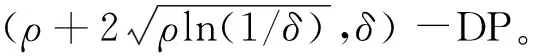
1.2 ADMM方法

在現有的分布式優化方式中，交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)是一種比較流行的策略。ADMM將全局問題分解為多個局部子問題，通過協調子問題的解最終得到全局問題的最終解。ADMM對輸入不敏感，還具有方法簡單、可解釋性高與收斂性易證明的優點。

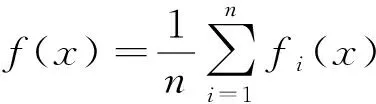
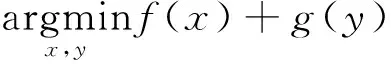
s.t.+=

(5)

通過優化這個目標函數，算法最終會收斂到某一個全局最優化或近似最優結果，從而解決了分布式中的一致性優化問題。

然而，滿足差分隱私的ADMM算法大多數都是去中心化的。比如動態zCDP(dynamic zero concentrated differential privacy)在每次迭代中引入具有線性衰減方差的高斯噪聲，在加速訓練的同時保持隱私保護的效能。K-Fed算法將聯邦學習與one-shot學習結合，只需一輪通訊即可完成K-Means算法的訓練。L-FGADMM將節點分為頭尾兩組，以確保每個節點只與其相鄰的兩個節點進行通信。此外，通過對神經網絡的每一層選擇不同的通信周期，L-FGADMM也減小了模型的通信負載。

1.3 分布式軟大間隔聚類

軟大間隔聚類(SLMC)由Chen于2013年提出。該模型將大間隔聚類(Maximum Margin Clustering, MMC)與軟聚類結合，在輸出空間進行聚類，而不是在數據空間中尋找一組聚類中心。具體來說，SLMC將簇中心錨定為個輸出標記的預定義編碼，計算決策函數和輸出空間中數據的軟隸屬度。它兼有大間隔聚類和軟聚類的優點，一方面具有尋求簇間最大間隔的決策函數，另一方面通過引入軟學習原理，使每個實例都屬于具有相應軟隸屬度的多個簇/聚類，并可通過軟隸屬度反映屬于單個簇的程度，從而具有較強的聚類能力。

對SLMC結合ADMM進行分布式改造之后，優化問題表示如下。

‖+‖‖

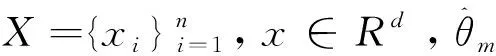
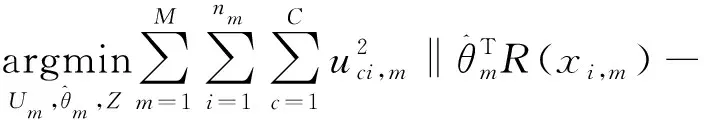
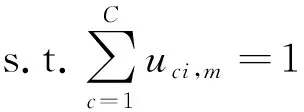
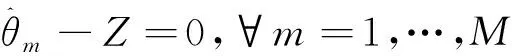
0≤,≤1,?=1，…，,=1，…，,

=1，…，

(6)

其中決策函數為：

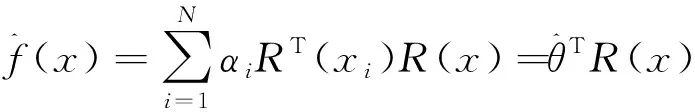
(7)

該算法通過引入RBF核的顯式特征映射近似，在不降低精度的前提下降低了時間復雜度。具體而言，該算法用傅立葉變換的蒙特卡羅逼近RBF核的特征映射。特征映射的方式如式(8)所述。

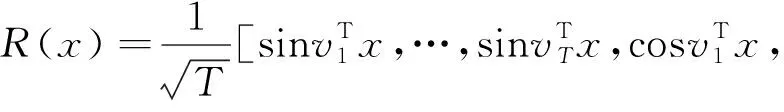
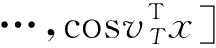
(8)

為RBF核對應高斯分布中隨機抽樣的向量。顯然，這種近似的精度會隨著樣本數量的增加而增加。在訓練中，將會根據具體場景考慮精度與復雜度的權衡來選擇一個適當的。

對其增廣拉格朗日優化格式實現采用交替迭代策略求解，可得迭代更新式：

)-1

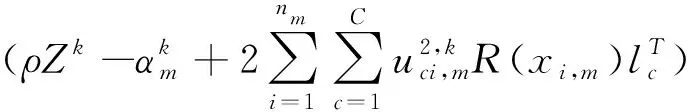
(9)

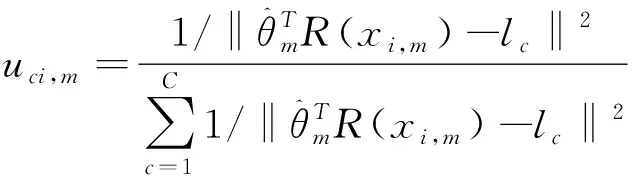
(10)

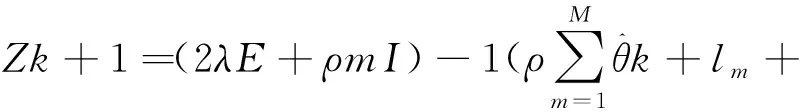
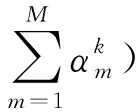
(11)

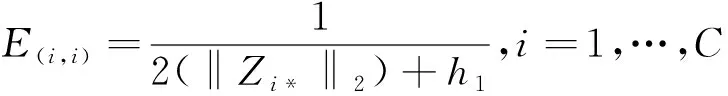
(12)

為了防止分母為0，故在分母處添加非負小量數。

(13)

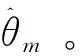
然而，目前還沒有關于差分隱私中心化SLMC算法的研究工作。因此，本文重點關注中心化差分隱私ADMM算法并提出了具有隱私保證的差分隱私軟大間隔聚類算法。

2 差分隱私軟大間隔聚類

2.1 差分隱私軟大間隔聚類

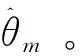
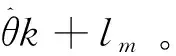
算法1 隱私保護軟大間隔聚類算法輸入:λ、ρ,停止參數εs、εr,,節點數M、映射特征維度D、輸入數據X;輸出:軟隸屬度矩陣Um;Each learner constructs random feature map Rm(x) with the same seed.Initialize Um by FCM,k=0.Upload Um+ξk+1mto the central server where ξk+1m～N(0,σ2Im+1D).Update Zk+1 in the central server by (11).Update θ^k+lm in parallel by (9).Update Uk+lm in parallel by (10).Update αk+lm in parallel by (13).k=k+1.If not obtaining convergence then go 3.10. Output Um at each learner.

2.2 隱私保護分析

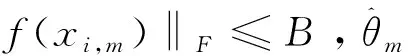
證明：根據式(6)可得：

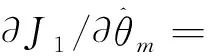
(14)

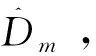
(15)

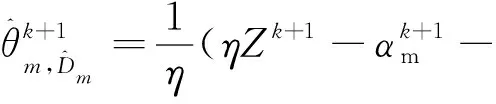
(16)

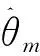
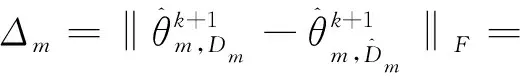
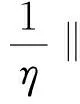
(17)

DP-SLMC的隱私保護效用如定理1所示。

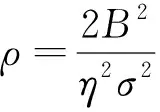
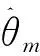
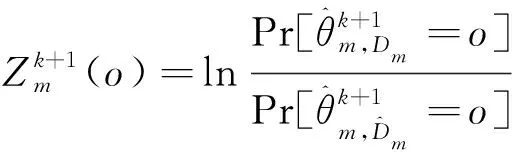
(18)

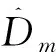
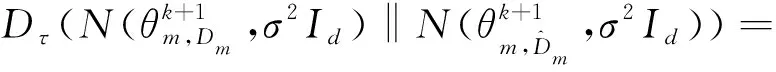
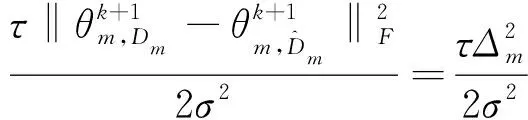
(19)

可得：

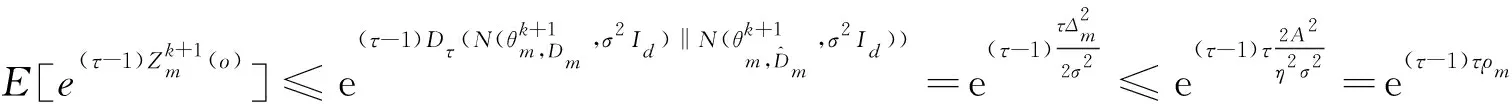
(20)

由于在整個迭代過程中每一輪都在更新與上傳系數矩陣，因此需要計算迭代過程中隱私損失的總和。

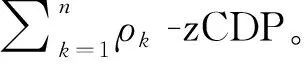
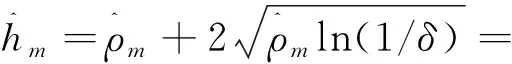
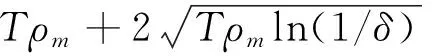
(21)

對于所有節點, DP-SLMC被(,)-DP限制的總隱私損失為：

(22)

3 實驗部分

本節將會通過 UCI 數據集來對本文提出的算法進行實驗，探究其性能。第3.1節中說明實驗相關設置。第3.2節引入本次實驗的對比指標。最后進行實驗并對實驗結果進行分析，驗證該方法的有效性。

3.1 實驗設置

本節將與未做隱私保護的分布式SLMC進行對比分析，進行性能比較。

我們對待對比的算法執行了20次獨立實驗，在每次實驗中使用最優的核與參數設置，并最終記錄這些實驗結果的平均值。所有的實驗都是在一臺具有英特爾(R)核心(TM)四核處理器(i7CPU@3.6GHz)和16.0GB內存的64位機器上進行的。表2描述了實驗數據集的屬性。

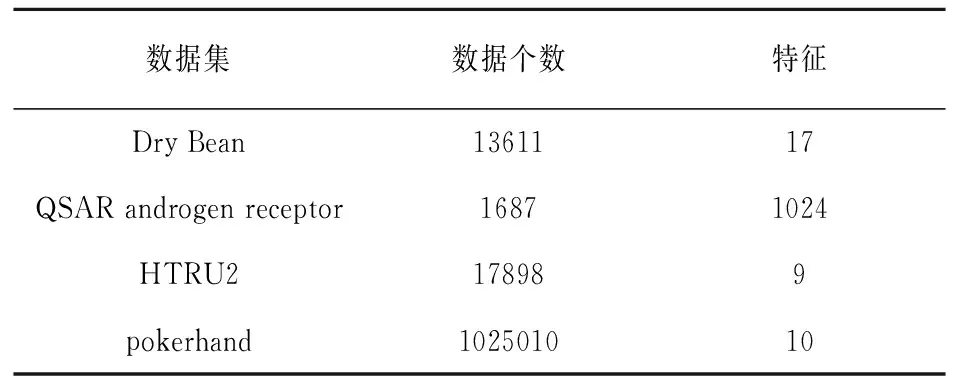
表2 數據集屬性

3.2 評估指標

雖然本文提出的是無監督分布式聚類算法，但在訓練時可通過帶類別標簽的數據集進行訓練。具體來說，在訓練時將類別信息剔除，然后將聚類的結果與真實標簽相比較。因此可采用聚類準確度(Clustering Accuracy, CA)來對算法進行性能評價。

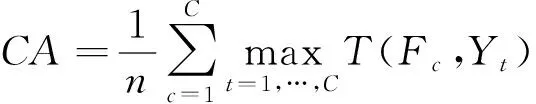
(23)

代表第聚類標簽，而代表真實標簽。(,)則代表屬于真實類別而被預測為類別的數據個數。我們通過比較預測聚類的標簽與真實標簽的方式，來確定聚類的準確度。顯然這個數值是越大越好。

此外，由于本文提出的是聯邦聚類算法，因此也將與未進行隱私保護的分布式軟大間隔聚類(DS-SLMC)進行收斂速度的對比。

3.3 實驗分析

圖1顯示了DP-SLMC算法與DS-SLMC算法目標函數值的對比。DP-SLMC與DS-SLMC的收斂曲線基本吻合，證明二者收斂速度并無太大差異。這個符合我們的直覺，即對交換變量加入符合差分隱私要求的噪聲對收斂過程與函數值影響較小。這個實驗證明即使加入噪聲，只要控制噪聲的大小，噪聲本身對模型的收斂無法造成較大的干擾。

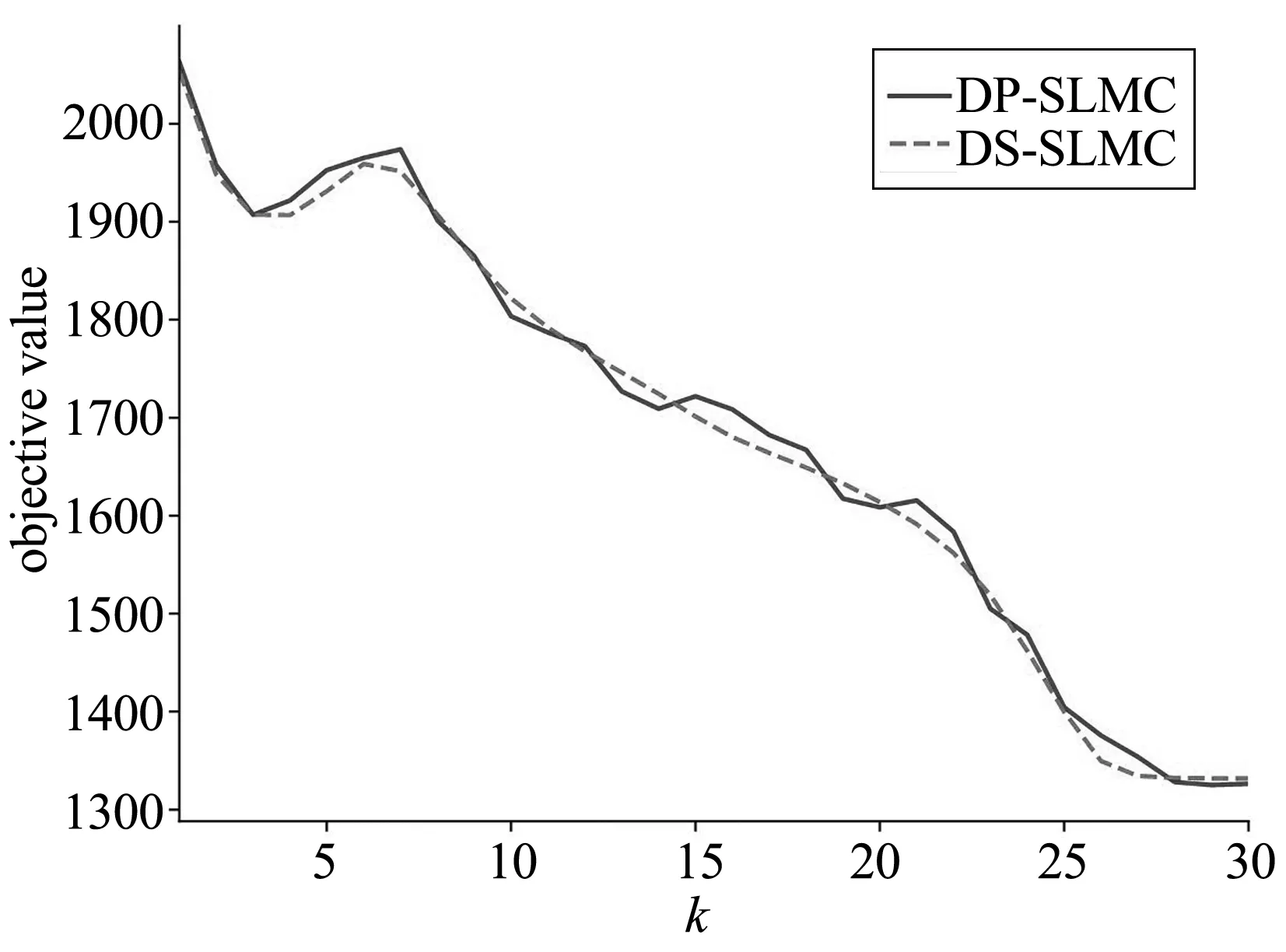
(a) Dry Bean

DP-SLMC在不同隱私預算下的目標函數值與準確度對比如圖2所示。在隱私預算較小的情況下，由于加入的噪聲過多，DP-SLMC的目標函數值與準確度相比，DS-SLMC算法表現不佳。但隨著隱私預算的增加，加入的噪聲逐漸減少，DP-SLMC的目標函數值與準確度越來越接近DS-SLMC算法。這個實驗說明，保證差分隱私的前提下，只要給予足量的隱私預算，噪聲本身對算法的準確度無法造成較大的干擾。在實際應用場景中，可通過準確率與隱私保護需求的權衡來決定隱私預算的大小，從而讓算法最大限度地滿足需求。

(a) Dry Bean

4 結 論

提出了一種聯邦軟大間隔聚類算法，將原聚類算法與隱私保護進行結合。為了實現這個目標，我們將原始的聚類問題中容易發生隱私泄露的通信環節加噪，使其滿足差分隱私準則，從而達到隱私保護效果。而實驗結果也表明本文提出的算法在降低隱私泄漏風險的前提下，依舊有貼近原聚類算法的性能與較快的收斂速度。此外，我們也通過實驗驗證DP-SLMC在不同數據集上都擁有良好的聚類性能。