中心差商公式變步長算法的計算終止條件

令鋒

（肇慶學院數學與統計學院，廣東 肇慶 526061）

1 問題的提出

數值微分是指將函數y=f(x)在給定點a的導數用點a附近節點上函數值的線性組合近似表示[1-2].科學研究與工程技術領域中的許多問題都需要計算函數f(x)在給定點的導數，當f(x)表達式復雜或函數僅由表格給出時，就需要進行數值微分，中心差商公式是數值微分采用的一種重要算法.

記h為步長，f(x)在節點a-h，a及a+h處的函數值分別為f(a-h)，f(a)和f(a+h)，則求f(x)在點a處一階導數的中點公式及截斷誤差分別為

求函數f(x)在點a處二階導數的三點公式及截斷誤差分別為

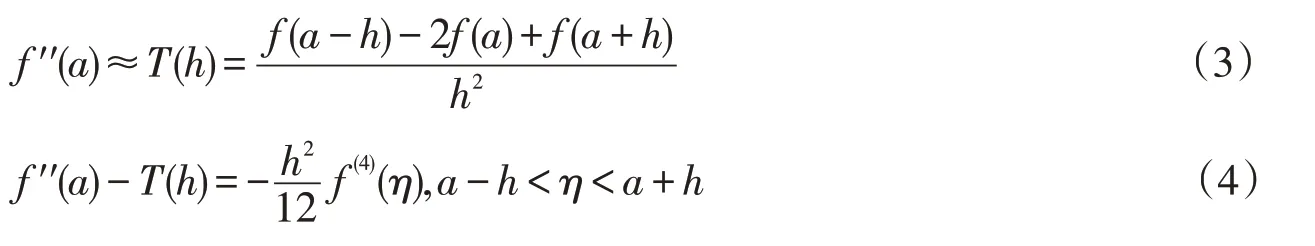
對公式（1），從截斷誤差角度分析，h越小計算結果越準確；但從舍入誤差或計算穩定性角度考慮，h越小，f(a-h)與f(a+h)的值將越接近，兩個相近數相減會導致有效位數嚴重損失，因而用中心差商公式（1）計算一階導數時步長不宜太小或太大，存在最優步長，當h取值小于最優步長后，計算誤差反而會增大[2-4].同理，采用公式（3）計算二階導數時也存在最優步長.

中心差商公式（1）及（3）都具有二階計算精度，且公式簡單，編程方便，是數值微分值得采用的方法.但由于步長很小時計算結果對步長變化敏感，大多數教材沒有進一步討論兩點公式與三點公式的計算機實現，個別教材中雖然提出宜采用變步長方法計算，但沒有給出詳細的分析、說明和示例，尤其是沒有給出計算終止條件[5]，因而編程實現算法存在困難.本文通過分析確定中心差商公式中最優步長面臨的問題，提出以計算結果滿足精度要求作為計算終止條件和以步長最接近最優步長作為計算終止條件兩種算法，以期能夠采用中心差商公式的變步長算法求得函數在給定點具有較高精度的一階及二階導數.

2 中心差商公式最優步長的確定

設f(a)，f(a-h)和f(a+h)的舍入誤差分別為ε0，ε1和ε2，ε=max{|ε0|,|ε1|,|ε2|}，則計算f′(a)與f′′(a)的舍入誤差分別為

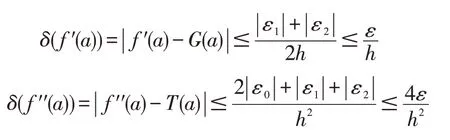
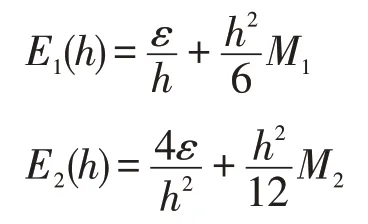
根據求極值的方法，要使誤差 取最小值，h應滿足

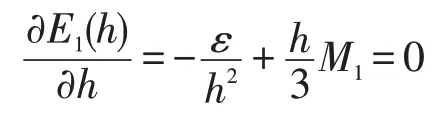
同理可得，使誤差E2(h)達到最小值的最優步長為

求出M1與M2的工作較繁瑣，在某些情形下甚至無法實現，從而確定最優步長面臨諸多困難.為獲得具有較高精確度的計算結果，通常采用中心差商公式變步長算法.以計算一階導數為例，首先選擇一個初始步長h0，為方便計算，通常取h0=1，利用公式（1）求出G(h0)，然后將步長減半得h1，再計算G(h1)，如此反復，使步長在逐步減半的過程中逐步接近最優步長，從而獲得精度較高的計算結果.因而，在變步長中心差商微分法的計算機實現過程中，確定正確的計算終止條件是算法得以實現的前提.

3 中心差商公式變步長算法的計算終止條件

設對初始步長h0經n次減半后得到的步長為h0，函數y=f(x)在點a相應的導數f′(a)及f″(a)的近似值分別為G(hn)和T(hn)，以下給出兩種計算終止條件.

3.1 滿足精度要求時終止計算

如果給定了計算精度要求ε，則前后兩次步長減半得到的導數近似值應滿足如下條件

此即給定精度要求時變步長數值微分法的計算終止條件.

上述算法容易編程實現且避免了直接計算最優步長，可望獲得理想的計算結果.但由于步長過小時誤差反而會更大，當要求的精度很高時，通過將步長逐步減半的方法可能無法獲得滿足精度要求的計算結果.實際計算時，為避免舍入誤差不斷增大出現較大誤差數值錯誤結果，可預設一個步長最大減半次數M，當步長減半次數超過最大減半次數時停止計算.

若以計算結果滿足精度要求作為計算終止條件，用三點公式（3）計算函數f(x)在點a的二階導數算法可描述如下：

算法1：數值微分的變步長三點公式算法

1） 輸入函數f(x)以及點a的值.

2）輸入計算精度要求ε及步長最大減半次數M.

3） 步長減半次數n=0,h=2-n=1，計算T0(f(a-h)-2f(a)+f(a+h))∕(h2).

3） 步長減半：n=1,h=2-n=1∕2，計算T1(f(a-h)-2f(a)+f(a+h))∕(h2).

4）如果 |T1-T0|＞ε，轉步驟5）；否則，轉步驟6）.

5）如果n≤M,則n=n+1，h=2-n,T0=T1,T1(f(a-h)-2f(a)+f(a+h))∕(h2)，轉步驟4）；否則，輸出出錯信息，轉步驟7）.

6）輸出計算結果T1.

7）結束.

3.2 步長最接近最優步長時終止計算

在步長逐步減半并接近最優步長hopt過程中，計算精度將越來越高，而步長小于hopt后，繼續對步長減半數值計算的誤差將會不斷增大.因此，經n-1次步長減半后得到的步長hn-1與最優步長hopt若滿足如下關系

相應的導數近似值則滿足如下條件

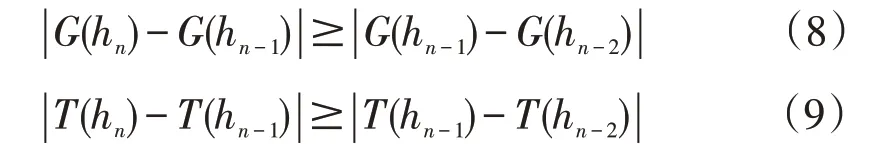
此即步長最接近最優步長時變步長數值微分法的計算終止條件,G(h)為步長為hn-1時f′(a)的近似值.

上述算法既可避免直接確定最優步長，又可獲得具有較高計算精度的計算結果，因而是一種非常實用的有效算法.

若以步長最接近最優步長作為計算終止條件，用變步長中點公式計算函數f(x)在點a的一階導數的算法可描述如下：

算法2：數值微分的變步長中點公式算法

1）輸入函數f(x)，輸入點a的值.

2）步長減半次數n=0，h=2-n=1，計算G0=[f(a+h)-f(a-h)]∕(2h).

3）步長減半：n=0，h=2-n=1∕2，計算G1=[f(a+h)-f(a-h)]∕(2h).

4）n=n+1，h=2-n，計算Gn=[f(a+h)-f(a-h)]∕(2h).

5）如果 |Gn)-Gn-1|≥ |Gn-1-Gn-2|，轉步驟6）；否則，轉步驟4）.

6）輸出計算結果Gn-1.

7）結束.

4 說明性算例

算例1用變步長三點公式計算函數f(x)=ex在輸入的點x處的二階導數近似值，要求誤差不超過0.5×10-6及0.5×10-9，并統計步長減半次數.

解 根據算法1編寫C語言程序生成Threepoints.com文件，計算結果如下：

請輸入要計算二階導數值的點a:1

請輸入精度要求epsilon:0.0000001

點a=1.000000處的二階導數為f′′(a)=2.7182818353，步長共減半11次.

請輸入要計算二階導數值的點a:1

請輸入精度要求epsilon:0.000000001

步長減半次數已達25次，仍未達到精度要求.

算例2取初始步長h0=1，用變步長中點公式計算函數f(x)=x2e-x在點x=1.0,1.5,…,5.0處的一階導數及誤差,并統計對應的最佳步長.

解 根據算法2編寫C語言程序生成文件Midpoints.com，計算結果如下：

5 總結

本研究提出了中心差商公式變步長算法計算機實現時的兩種計算終止條件，若以計算結果滿足精度要求作為計算終止條件，可避免直接計算最優步長，方法簡單，設計程序方便，可以獲得滿足一般精度要求的計算結果.但當要求的精度很高時，此方案的計算精度可能不能令人十分滿意.若以步長最接近最優步長作為計算終止條件，既可避免直接確定最優步長，又可獲得具有較高計算精度的計算結果，因而是一種非常實用的有效算法.