改進的UKF乒乓球軌跡預測算法

尹 朵，丁文龍，邱 崧

（華東師范大學 通信與電子工程學院，上海 200241）

0 引 言

近年來，機器視覺技術在國內外獲得快速發展。在機器視覺研究中，實現對目標物體的識別與跟蹤具有重要意義。單純的目標檢測跟蹤并不能準確預判下一時刻物體的運動狀態和位置，物體的軌跡預測逐漸成為機器視覺領域的重點和難點。

目前常用的軌跡預測方法主要包括：基于傳統多項式擬合的動態軌跡預測、基于卡爾曼濾波的動態軌跡預測、基于神經網絡的動態軌跡預測。其中，基于傳統多項式擬合的動態軌跡預測通過擬合含有1個參數的階多項式，在原始數據足夠多的情況下，逼近函數曲線，使得誤差最小化，得到運動物體軌跡預測的函數曲線，該原理簡單、易于實現、建模迅速，適用于小數據量、簡單的軌跡預測，缺點是精度不高，擬合階數越高、系統越發散；基于卡爾曼濾波的動態軌跡預測通過前一時刻的估計值和當前時刻的觀測值更新對狀態變量的估計，實現對下一時刻的軌跡位置的預測，該方法對運動狀態頻繁改變的運動目標具有很好的適應性，但無法長時間進行軌跡預測；基于神經網絡的動態軌跡預測可以有效地學習運動目標的歷史運動狀態，利用機器學習方法建立輸入輸出的映射關系，有效實現運動目標的軌跡預測，該方法可以充分逼近非線性系統，軌跡預測結果精確，但需要依賴大量數據訓練模型，實時性差。

近年來，對乒乓球軌跡預測的研究主要是圍繞無旋球展開，對旋轉球的研究更多地集中在旋轉球識別分類上，或采用機器學習的方式進行旋轉球的軌跡預測。文獻［1］基于4臺高速1394火線相機和一臺功能強大的工業PC構成的高速視覺系統，提出了一種取決于摩擦系數和垂直恢復系數的旋轉速度的新型物理彈跳模型，用于球軌跡預測。文獻［2］構建了一個集成的視覺系統來觀測乒乓球的旋轉運動，并利用位置和自旋信息，通過擴展卡爾曼濾波器（EKF）來實現軌跡預測。文獻［3］提出了一種通過反向傳播神經網絡（BPN）進行軌跡預測的方案，通過2個神經網絡分別對碰撞前后的飛行拋物線進行學習訓練，通過第一拋物線的10個點即可預測軌跡。文獻［4］通過構建空氣動力學模型以及回彈模型對乒乓球軌跡進行預測，并根據預測的軌跡計算擊球點球的狀態。

上述方法在一定程度上提高了軌跡預測的精度，但存在硬件要求高、算法復雜、忽略旋轉球角速度等問題。本文提出了一種雙目視覺下基于無跡卡爾曼濾波及運動學模型的軌跡預測算法，首先通過無跡卡爾曼濾波的方式對碰撞前軌跡進行預測；預測到落點后，采用碰撞模型及運動學模型預測碰撞后軌跡。該方法能夠更加準確地實現乒乓球的軌跡預測，且對視覺系統硬件性能要求較低。經實驗驗證，該方法對碰撞后乒乓球軌跡預測實時性更高，預測較準確。

1 改進的基于UKF的乒乓球軌跡預測算法

乒乓球軌跡的預測是指通過乒乓球的部分三維世界坐標預測乒乓球的軌跡，從而確定乒乓球的落點。對乒乓軌跡預測的要求主要分為實時性及準確性兩部分。采用傳統多項式擬合方法預測乒乓球軌跡的方法實時性較好，但對于旋轉乒乓球的預測效果較差；基于神經網絡的軌跡預測方法可以對旋轉乒乓球軌跡進行有效預測，但需要大量數據訓練模型。本文采用無跡卡爾曼濾波及運動學模型對旋轉乒乓球軌跡進行預測，可以兼顧實時性的同時保證旋轉球預測的準確性。

1.1 基于UKF的乒乓球碰撞前軌跡預測

乒乓球在運動過程中，由于在擊球瞬間球拍對乒乓球作用力、即馬格努斯力的方向不一定完全通過球心，乒乓球在飛行過程中會產生旋轉。旋轉的乒乓球存在自身角速度，如果直接將其視為質點而忽略角速度，在軌跡預測的結果中會出現較大誤差。飛行過程中，旋轉的乒乓球主要會受到重力、空氣阻力和馬格努斯力三個力的作用，影響馬格努斯力的主要因素就是角速度，若使用硬件設備直接獲取角速度需要配備超高速攝像機或紅外設備，成本昂貴，實驗條件難以保證。本文采用UKF間接估計角速度這一未知狀態。

UKF是一種基于最小方差估計準則的非線性高斯狀態估計器，采用無損變換（Unscented Transform，UT）來近似系統狀態的后驗均值及后驗協方差，所需估計時間更短，精確度更高。

離散非線性系統可以用一個過程方程和一個觀測方程表示，其數學表述可寫為：

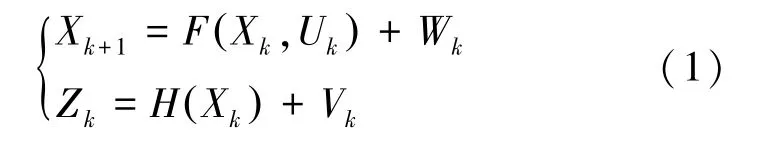
其中，為狀態過程函數；為觀測過程函數；U為時刻輸入向量；Z為時刻觀測向量；W和V分別為時刻過程噪聲和量測噪聲，兩者互不相關且均為高斯白噪聲；X為時刻運動狀態向量。

1.1.1 系統過程方程構建

對于旋轉的乒乓球，過程方程是非線性的，而觀測方程是線性的。采用9維向量表示乒乓球的狀態變量，具體公式如下：

其中，p，p，p表示乒乓球在，，軸的坐標；v，v，v分別表示乒乓球在，，軸的速度；ω，ω，ω分別表示乒乓球在，，軸的角速度。

觀測向量用三維向量表示，即通過雙目視覺得到的乒乓球三維坐標信息，見式（3）：

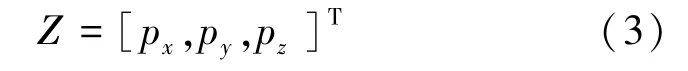
定義 ［p，p，p，v，v，v，ω，ω，ω］為系統時刻的9維狀態向量，構建乒乓球運動模型的系統過程方程，列出的方程分別如下：

其中，W（1，2，3，…9）為時刻9維零均值過程噪聲向量中的各項；系數為空氣阻力因子；為馬格努斯力因子；‖‖表示第1時刻3個方向線速度的模值。

進一步，研究推得的數學計算公式可寫為：

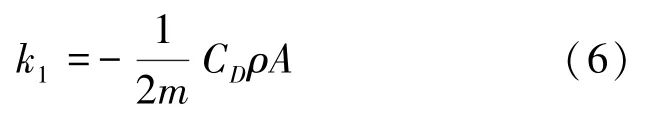
其中，C取決于乒乓球表面粗糙程度；為空氣密度；為乒乓球最大橫截面積。

同時，研究推得的數學計算公式可寫為：

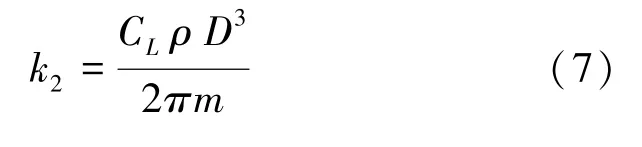
其中，C為升力系數；為乒乓球直徑；為乒乓球質量。

綜上可得，時刻乒乓球在，，坐標軸的角速度可由如下公式計算求得：

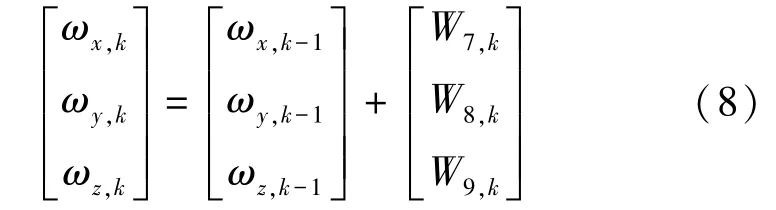
至此，乒乓球運動模型的系統過程方程構建完成。

1.1.2 系統觀測方程研究

乒乓球運動模型的系統觀測方程，表示形式為：

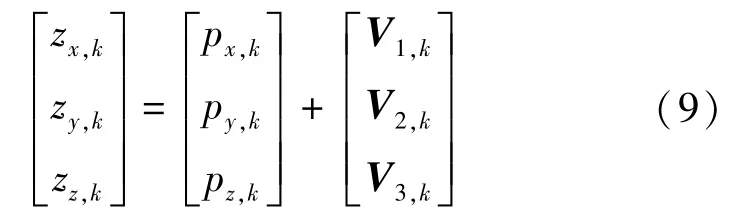
其中，V（1，2，3）為時刻三維零均值觀測噪聲向量。

W與V線性無關，且滿足式（10）：

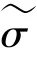
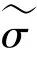
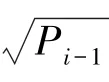
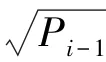
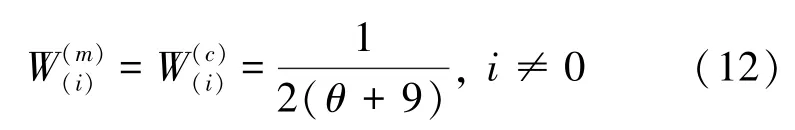
在這一部分，關于初始值的運算可給出研究表述如下。

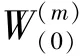
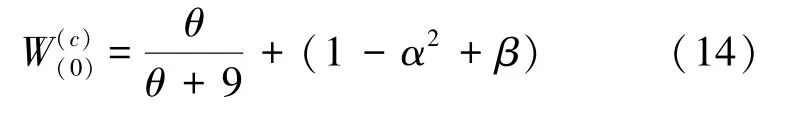
其中，表示采樣點的分布信息。

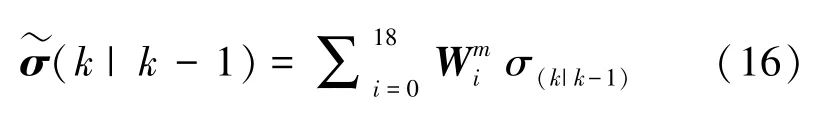
并計算下一步誤差協方差（1），數學定義式如下：

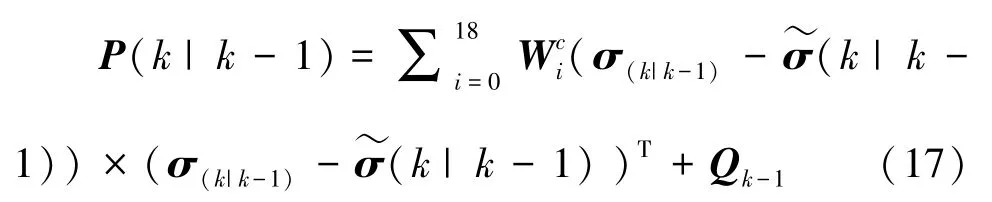
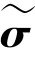
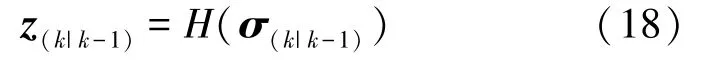
計算誤差協方差（1），對此可寫為如下形式：

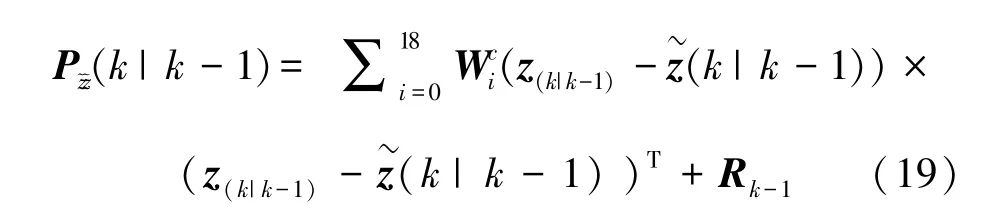
計算互協方差（1），可由下式確定：

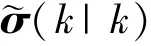
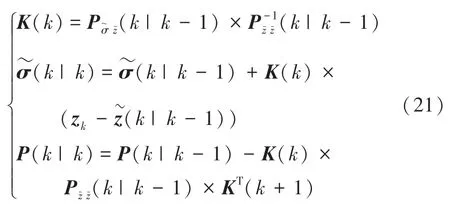
1.2 基于運動學的乒乓球碰撞后軌跡預測

快速地獲取碰撞后乒乓球的軌跡，以便機械臂具有充足的時間調整姿態和位置將乒乓球擊回，由于乒乓球碰撞后運動狀態發生改變，碰撞后傳統UKF乒乓球軌跡預測的收斂時間更長，預測誤差逐漸增大。本文通過構建反彈后簡單物理運動模型（SPM）的方式預測碰撞后的乒乓球軌跡。

由于帶有馬格努斯力的乒乓球物理運動模型構建復雜、且馬格努斯力較小，在構建碰撞后的乒乓球物理模型時，忽略馬格努斯力。乒乓球運動時的受力分析如圖1所示。

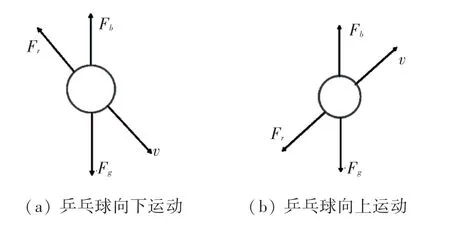
圖1 乒乓球運動時受力分析圖Fig.1 Force analysis diagram during the moving of table tennis

圖1中，F為乒乓球所受重力；F為空氣阻力；C為空氣阻力系數；F為空氣浮力；為乒乓球的速度。

由于空氣浮力數值太小，不加入后續模型推導計算。乒乓球所受各力的數學公式具體如下：

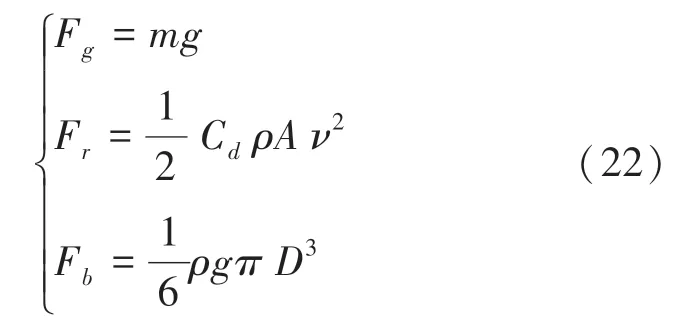
其中，C為空氣阻力系數；為空氣密度；為乒乓球最大橫截面積；為乒乓球直徑。

由于空氣浮力數值太小，不加入后續模型推導計算。

對式23()積分可得，時刻乒乓球在軸上的分速度v的數學公式可寫為：

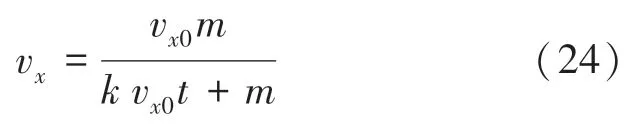
其中，v表示0時刻乒乓球在軸上的初始分速度。

乒乓球時刻在軸上分速度v，以及時刻乒乓球在軸的坐標p的計算公式分別如下：

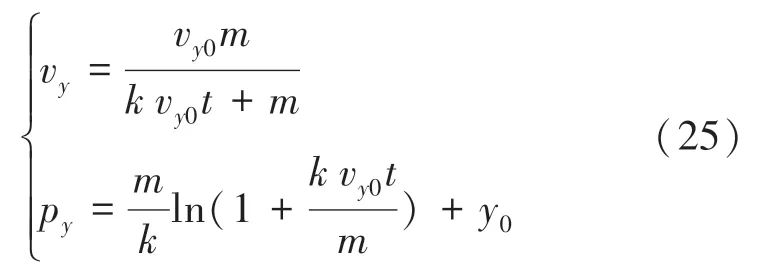
其中，v表示0時刻乒乓球在軸上的初始分速度，表示0時刻乒乓球在軸上的初始位置坐標。

乒乓球在軸方向受到空氣阻力及重力的影響，當v＞0時，根據乒乓球受力分析及牛頓第二定律可得式（26）：

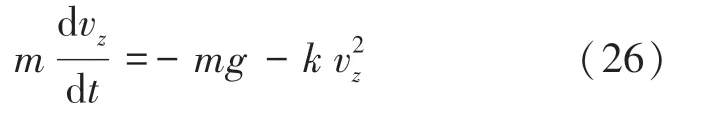
對式（26）積分可以得時刻乒乓球在軸上的分速度v的數學公式可寫為：

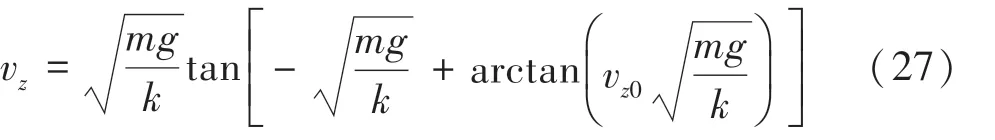
其中，v表示0時刻乒乓球在軸上的初始分速度。

對式（27）中的速度v在0時刻積分可得，時刻乒乓球在軸的坐標p，可由下式計算求得：

其中，表示0時刻乒乓球在軸上的初始位置坐標。

當v≤0時，根據乒乓球受力分析及牛頓第二定律可得式（29）：

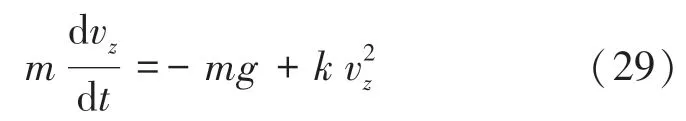
對式（29）積分可以得到：

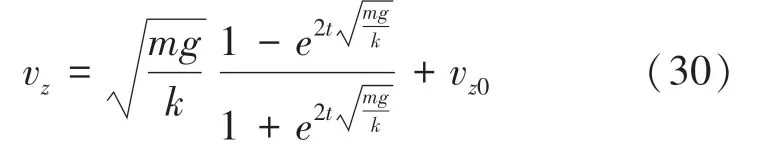
對式（30）中的速度v在0時刻積分可得，時刻乒乓球在軸的坐標p，運算公式見式（31）：

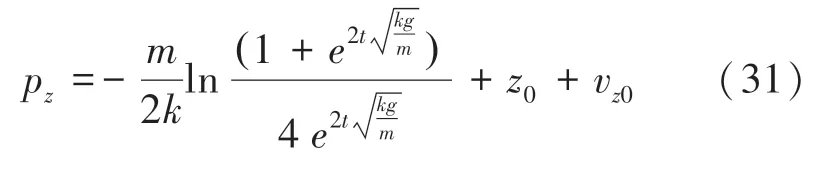
乒乓球與桌面發生碰撞時，由于球速、球的運動方式不同，在水平方向和垂直方向上的摩擦系數和衰減系數也不同。構建乒乓球的反彈模型，計算反彈后乒乓球在，，軸的速度v，v，v，推得的數學公式分別如下：

其中，k、k、k、b、b表示反彈擬合參數，v、v、v分別表示，，軸反彈前乒乓球的速度。

利用乒乓球碰撞反彈的軌跡擬合，采樣多條乒乓球反彈軌跡，記錄反彈前后坐標，利用最小二乘法擬合確定反彈擬合參數。

2 實驗結果對比分析

在搭建高速運動的乒乓球系統中驗證本文算法的有效性。乒乓球機器人系統中的圖像采集設備為USB工業攝像機，幀率為120 fps。軌跡預測的數據采樣時間間隔為20 ms。傳統UKF方法與SPMUKF方法軌跡預測結果對比如圖2所示。

由圖2可知，傳統UKF預測方法的結果在軸上誤差不超過10 mm，、軸誤差不超過20 mm。由于UKF算法需要測量值的輸入不斷修正狀態估計量，從而更好地預測下一個點的位置，因此當只輸入部分數據時，隨著時間的推移，軌跡預測值會出現較大誤差。而改進后的UKF乒乓球軌跡預測算法通過對物理模型的建模，在乒乓球反彈后的軌跡預測中整體誤差有所降低，、軸方向誤差在10 mm內，軸誤差在15 mm內，相較于傳統的UKF預測方法，誤差有一定減少。

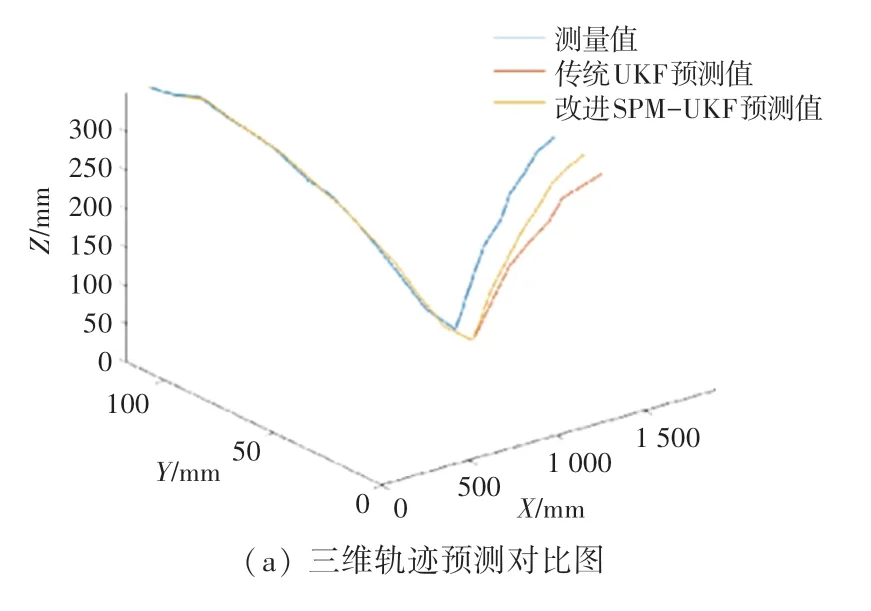
圖2 不同算法結果對比圖Fig.2 Comparison of results with different algorithms

3 結束語

本文針對傳統的UKF算法在乒乓球碰撞后軌跡預測誤差隨時間增大的問題，提出了改進的UKF乒乓球軌跡預測算法。對乒乓球碰撞前的軌跡采用UKF算法預測，在碰撞后采用簡單物理運動模型預測乒乓球的軌跡。實驗證明改進的UKF乒乓球軌跡預測算法可以一定程度上提高軌跡預測的精度，為后續乒乓球機器人擊球工作的開展提供了保障。