Tu方程的留數對稱及其精確解①

呂梓帆

西北大學 數學學院，西安 710127

許多物理現象都可以用非線性演化方程來描述，一直以來受到學者的廣泛關注和研究． 科學家們運用了各種方法來構造非線性系統的解，并研究發現利用對稱方法構造其精確解是一種很有效的方法[1-2]． 文獻[3]發現非線性系統Painlevé截斷展開的奇異流形的留數是非局域對稱，稱之為留數對稱[3]．目前，很多方程都可以利用上述方法進行對稱約化，如Korteweg-de Vries方程、Kadomtsev-Petviashvili方程、Burgers方程、色散長波方程等[4-11]．

本文主要對Tu方程

(1)

1 非局域留數對稱及B?cklund變換

Tu方程(1)的Painlevé截斷展開式為

(2)

其中：f表示奇異流形；u0，u1，v0，v1，v2，f都是關于x，t的函數．

將展開式(2)代入到式(1)中，合并f的同次冪，有

(3)

令其各次冪項的系數都為零，可解出系數：

(4)

同時f需要滿足下面的Schwarzian形式：

(5)

根據展開式(3)，如果{u，v}是方程(1)的解，則f的零次冪的系數為零的表達式說明{u0，v0}也滿足Tu方程(1)，從而得到如下自B?cklund變換定理[3]：

定理1如果{u，v}是Tu方程(1)的解，則

(6)

就是方程(1)的一個自B?cklund變換．

我們知道，Schwarzian方程(5)在M?bious變換

的作用下是形式上保持不變的，即方程(5)容許如下的3種對稱：

σf=c1，σf=c2f，σf=c3f2

(7)

其中c1，c2，c3為任意常數．特殊地，取a=d=1，b=0，c=-ε，其中ε為任意群參數，則此時Schwarzian方程(5)式的對稱為

σf=f2

(8)

根據上述分析，可以得到Tu方程的非自B?cklund變換定理如下．

定理2如果f是Schwarzian方程(5)的解，則

(9)

是f和Tu方程的解{u0，v0}之間的一個非自B?cklund變換．

2 留數對稱的局域化

Tu方程(1)的對稱方程為

(10)

與式(3)中的奇異流形f的留數作比較，可以知道{u1，v1}為Tu方程(1)的解{u0，v0}的留數對稱，即：

(11)

其中{u0，v0}和f滿足非自B?cklund變換(7)． 為了方便表示，不失一般性，本節我們用{u，v}代替{u0，v0}進行描述． 為將留數對稱進行約化， 首先對其進行局域化， 解決如下初值問題：

(12)

其中ε為群參數．將Tu方程進行適當延拓，引入輔助變量：

g=ft，l=fx，h=gt，k=gx

(13)

則解{u，v}的非局域留數對稱(11)可以被局域化，得到延拓系統(1)，(5)，(13)的Lie點對稱，即：

(14)

相應的Lie點對稱的向量場表達式為

(15)

解如下初值問題：

(16)

可得到下面的對稱群變換定理．

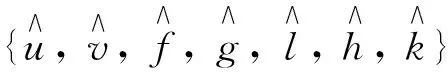
(17)

3 CRE可解性及精確解結論

根據CRE方法，Tu方程(1)的解有如下展開式：

(18)

其中w=w(x，t)，R(w)是Riccati方程：

Rw=l0+l1R+l2R2

(19)

的解，l0，l1，l2是任意常數．將表達式(18)和(19)代入方程(1)中，令R(w)的各次冪前面的系數為零，可得

(20)

同時，函數w滿足下面方程：

(21)

由此可知，Tu方程(1)是CRE可解的．

根據孤立波解通常可用雙曲函數表示的特點，我們可將該方程用tanh函數展開方法求解．取式(19)中l0=1，l1=0，l2=-1，此時Riccati方程的特解為

R(w)=tanh(w)

(22)

那么可以得到

(23)

此時我們稱Tu方程是CTE可解的．

為了得到Tu方程的精確解，我們考慮以下兩種特殊情形，說明Tu方程的孤立波解的具體形式．

例1考慮w為如下形式：

w=kx+ht+b

(24)

其中k，h，b為任意常數，將其代入式(18)及式(1)中，令R(w)的所有次冪的系數為零，得到代數方程組如下：

(25)

通過解上述方程組，得到一組非平凡解為

(26)

由此得到Tu方程(1)的孤立波解為

(27)

取參數值{k=1，h=3，b=0}，利用MAPLE軟件，我們得到孤立波相互作用解的波形圖．圖1為解u的波形圖，是反扭結型孤立波，圖2為解v的波形圖，是鐘型孤立波．

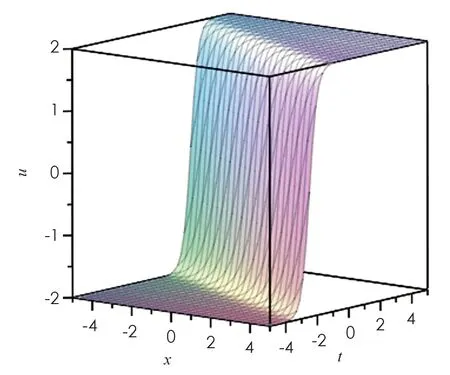
圖1 在例1條件下解u的波形圖

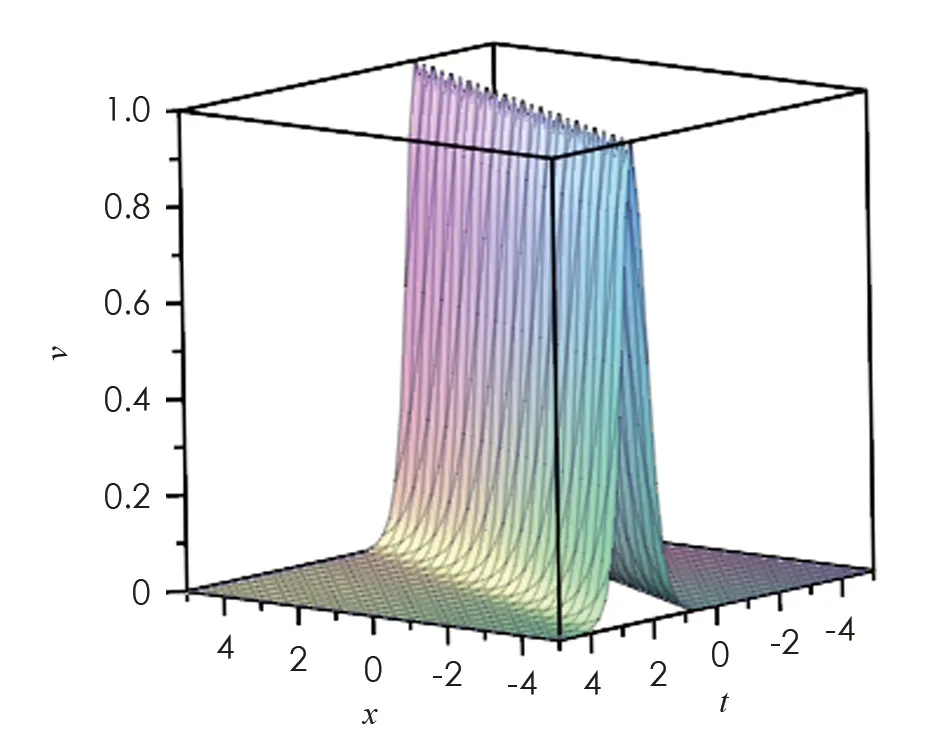
圖2 在例1條件下解v的波形圖

例2我們考慮w具有如下形式：

w=k1x+h1t+W(X)，X=k2x+h2t

(28)

其中k1，k2，h1，h2都是任意常數，將式(28)代入式(21)中，我們發現W1=WX滿足如下橢圓方程：

(29)

式中

(30)

其中h1，h2，C2，C3為任意常數．則Tu方程的解具有如下形式：

(31)

接下來討論方程(1)的非線性波之間的相互作用解．取方程(29)的解W為如下形式：

W=sn(X，m)，X=k2x+h2t

(32)

其中sn(X，m)為橢圓函數，聯立式(1)，(28)，(32)可解得系數的一組非平凡解為：

(33)

因此方程的解為

(34)

參數取值為{m=0.999，k2=1，h2=3}，利用MAPLE軟件，我們得到Tu方程(1)解的波形圖，其中： 圖3為解u的波形圖，描述了橢圓周期波和反扭結型孤立波的相互作用； 圖4為解v的波形圖，描述了橢圓周期波和鐘型孤立波的相互作用．

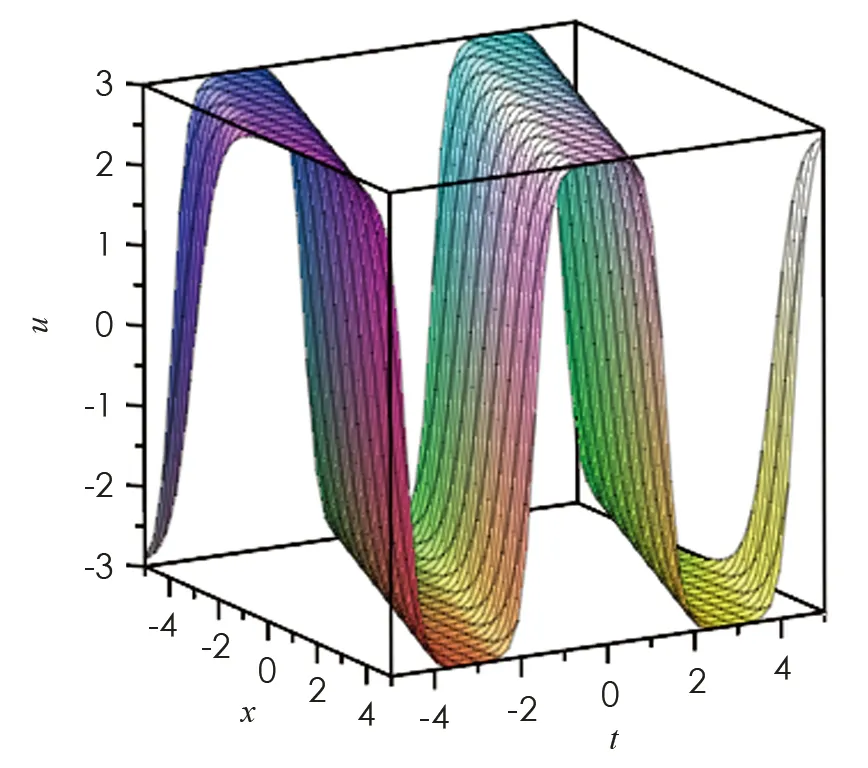
圖3 在例2條件下解u的波形圖

圖4 在例2條件下解v的波形圖

4 結束語

本文首先得到Tu系統的非局域留數對稱，并分析其B?cklund變換，通過引入合適的新變元將其局域化后利用Lie的第一基本定理得到了有限變換定理．之后說明了Tu系統具有CRE可解性，并利用MAPLE軟件作圖描述Tu系統的不同形狀的孤立波和周期波之間的相互作用．