對稱群Sn(17≤n≤19)的一個新刻畫①

李夢瑤， 楊國川， 晏燕雄

1.西南大學 數學與統計學院，重慶 400715； 2.208水文地質工程地質隊，重慶 400700

本文涉及的群均為有限群．設G是有限群，

πe(G)={|x|：x∈G}

另外，mi(G)表示群G的第i高階元素的階，

m1(G)=max{|g|：g∈G}

Gp表示群G的一個Sylowp-子群．pα‖|G|表示pα||G|但pα+1|/|G|，其中α是非負整數．其他未說明的符號和術語都是標準的(見文獻[1])．

眾所周知，利用群的數量性質研究群結構一直是群論研究的熱點，而如何用盡可能少的數量關系來刻畫群的結構是群論研究中非常有意義的課題．群的階和群中元素的階 (簡稱兩階)是群的兩個最基本的數量條件，這兩個數量關系對群結構有著非常重要的影響．關于該問題，施武杰教授在20世紀80年代提出過如下猜想(這一猜想被列入文獻[2]中)：

猜想設G為有限群，H為有限非交換單群，則G?H當且僅當πe(G)=πe(H)且|G|=|H|．

該猜想被文獻[3]最終證明．此后，許多群論學者嘗試弱化兩階的條件來刻畫群的結構．例如，文獻[4-10]提出用群的階以及最高階元素的階刻畫有限單群，并成功刻畫了散在單群、K3-單群、K4-單群、部分李型單群、部分交錯群An(5≤n≤13)及對稱群Sn(5≤n≤7)．文獻[11]用群的階以及最高階元素的階刻畫了部分K5-單群．文獻[12]證明了群G的同階交換子群的個數之集為{1，3}等價于群G的同階子群的個數之集為{1，3}．文獻[13]討論了與最高階元素有關的幾個數量條件對Conway單群和Fischer單群的結構的影響．文獻[14]討論了最高階元素個數為6p2q的有限群．文獻[15]用群的階以及mi(G)(i=1，2，3)刻畫了對稱群Sn(8≤n≤15)．

本文將繼續上述相關問題的研究， 研究群的某些特殊高階元素的階對群結構的影響，主要結果如下：

定理1設G是有限群，G?S17當且僅當

(i) |G|=|S17|；

(ii)mi(G)=mi(S17)(i=1，2，3)．

定理2設G是有限群，G?S18當且僅當

(i) |G|=|S18|；

(ii)mi(G)=mi(S18)(i=1,2,3,4)．

定理3設G是有限群，G?S19當且僅當

(i) |G|=|S19|；

(ii)mi(G)=mi(S19)(i=1，2)．

定理1的證明

必要性顯然，下面只證充分性．

由文獻[16]得

|G|=215·36·53·72·11·13·17

m1(G)=210m2(G)=140m3(G)=120

步驟1 證明G有一個正規群列1?_N?M?G，使得M/N為非交換單群，且11·17||M/N|．

設

G=G0?_G1?_ …?_Gn-1?_Gn=1

為G的主群列，則存在i，使得

π(Gi)∩{11，17}≠?π(Gi+1)∩{11，17}=?

設M=Gi，N=Gi+1，則G?_M?N?_ 1為群G的正規列，且M/N為G/N的極小正規子群．

斷言{11，17}?π(M)．若否，設11?π(M)，17∈π(M)，則11∈π(G/M)．令

M17∈Syl17(M)G11∈Syl11(G)

則G11可共軛作用在M上．由文獻[17]的引理8.3.1可知M中存在G11-不變的Sylow 17-子群M17， 則

|G11/CG11(M17)|||Aut(M17)| 11 ∈π(CG11(M17))

故187∈πe(G)，矛盾于m2(G)=140．于是11 ∈π(M)．

同理可證，不存在11 ∈π(M)，且17?π(M)．因此{11，17}?π(M)．

下證M/N為非交換單群．

因為

{11，17}?π(M)π(N)∩{11，17}=?

故

{11，17}?π(M/N)

M/N為G/N的極小正規子群，且17|||G|，故M/N必為非交換單群，且11·17||M/N|．

步驟2 證明M/N?A17．

由步驟1知M/N為非交換單群，|M/N|||S17|且11·17||M/N|，

|G|=215·36·53·72·11·13·17

由文獻[16]知M/N?A17．

步驟3 證明G?S17．

若M/N?A17，由文獻[15]的引理2知G中存在正規子群C，使得

若|C|=2，則G/C?A17．故G?2×A17，或G?2·A17，則m3(G)=126．這與m3(G)=120相矛盾．

若|C|=1，則G/C?S17，即G?S17．

綜上所述，定理1得證．

定理2的證明

必要性顯然，下面只證充分性．

由條件知

|G|=216·38·53·72·11·13·17

m1(G)=210m2(G)=180m3(G)=168m4(G)=140

類似于定理1的證明可以得到，G有一個正規群列1?_N?M?_G，使得M/N為非交換單群，且11·17||M/N|．由文獻[16]知M/N?A17，A18．

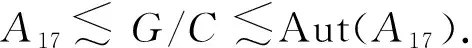
1 charD1charD2char … charDn=C

使得Di/Di-1為初等交換群，其中Di-1為Di的極大正規子群．從而一定存在i，使得|Di/Di-1|=3，32．于是

則

|G/Di-1/CG/Di-1(Di/Di-1)|||Aut(Di/Di-1)|

由

G/C?G/Di-1/C/Di-1

可得G/Di-1包含A17這個截斷．由A17有55階元，且

|G/Di-1/CG/Di-1(Di/Di-1)|||Aut(Di/Di-1)|

可得CG/Di-1(Di/Di-1)有55階元．故G有165階元，這與m4(G)=140矛盾．

若M/N?A18，由文獻[15]的引理2知，存在C?_G使得

如果|C|=2，則G/C?A18，從而G?2×A18，2·A18，這時m4(G)=154，矛盾．

如果|C|=1，則G/C?S18，即G?S18．

綜上所述，定理2得證．

定理3的證明

必要性是顯然的，下面只證充分性．

已知

|G|=216·38·53·72·11·13·17·19

m1(G)=420m2(G)=210

類似于定理1的推理知，G有一個正規群列1?_N?M?_G，使得M/N為非交換單群，且17·19||M/N|，其中19=max{p：p∈π(M/N)}，由文獻[16]知，M/N?A19，J3．

若M/N?J3，由文獻[15]的引理2知，存在G的正規子群C，使得

從而

|C|=29·33·52·72·11·13

或

|C|=28·33·52·72·11·13

令

C13∈Syl13(C)G19∈Syl19(G)

從而G19可共軛作用在C上．由文獻[17]的引理8.3.1可知C中存在G19-不變的Sylow 13-子群C13，則

|G19/CG19(C13)|||Aut(C13)| 19 ∈π(CG19(C13))

故247∈πe(G)，這與m2(G)=210矛盾，故M/NJ3，于是M/N?A19．由文獻[15]的引理2可知，G中存在正規子群C，使得

如果|C|=2，則G/C?A19．故G?2×A19，2·A19，從而m2(G)=330，這與m2(G)=210相矛盾．

如果|C|=1，則G?S19．

綜上所述，定理3得證．

注定理1中的m3(G)不能缺少，否則G?2×A17，2·A17； 定理2中的m3(G)與m4(G)不能缺少，否則G?2×A18，2·A18．