面向SOI波導-單模光纖耦合的硅微透鏡設計
李雄飛,韓明璽,疏 靜,王 雷,桂 桑,岳玉濤,顧文華
(1.南京理工大學電子工程與光電技術學院,江蘇 南京 210000;2.無錫市德科立光電子技術股份有限公司,江蘇 無錫 214000;3.江蘇集萃深度感知技術研究所有限公司,江蘇 無錫 214000)
1 引 言
實現硅波導與光纖的高效耦合同時滿足較高集成度是硅基光子技術用于高速光纖通信必須解決的關鍵問題之一。絕緣體上硅(SOI)波導的Si-SiO2-Si結構對光有很好的約束力,且相比其他材料的光波導如SiN、Ge∶SiO2等,可以做到更高的集成度,并于主流半導體硅工藝高度兼容,前景廣闊。因此,本文著重研究了基于硅微透鏡對SOI波導和單模光纖進行高集成度耦合的問題。
除了常見的楔形、光柵、光纖端面拉錐等耦合結構[1-6],使用透鏡結構對波導和光纖耦合也一直是被研究的重點之一。但是常規尺寸的耦合透鏡多為從傳統光學衍生發展的分立式的二氧化硅透鏡,使用于半導體發光器件/波導至單模光纖的遠場耦合[7-12],其工藝成熟,有較大的對準容限,但體積過大,成本較高,不利于集成和封裝。因此,在硅基平臺直接集成的微型耦合結構無疑是具有研究價值和應用前景的,這就要求在微小結構尺寸和較近距離盡量減少二者之間的模場尺寸失配(SMF-Core∶9.86 μm,SOI∶<3.5 μm)和折射率失配(SMF-Core∶1.468,Si∶3.45)帶來的耦合損耗。
相比于納米線波導,微米級的波導意味著可以承受更高光功率和更好的工藝容錯性,最關鍵的是能夠容易與單模光纖的光場尺寸匹配。最近,關于厚硅3 μm的SOI工藝已經展現出實用階段的集成潛力,如芬蘭國家科技研究院VTT[13]的3 μm波導工藝,已經做到0.1 dB/cm 的低傳輸損耗,端面耦合損耗可低至0.5 dB。另外,英國Rockley[14]的3 μm波導工藝降低條形波導(Strip-waveguide)的傳輸損耗至0.3 dB/cm,最高可承受10 W的光功率;而且,Rockley通過Euler-band結構將其彎曲直徑降至1.3 μm,解決了大截面波導的彎曲損耗問題。
因此,本文根據高斯光束傳播理論設計了一種基于3 μm SOI波導工藝邊緣集成的硅微透鏡耦合結構(如圖1所示),并使用光束傳播(Beam Propagation Method,BPM)算法仿真分析其在1550 nm波長下的近場耦合效果,仿真結果表明可實現近場90 %耦合效率,該設計可為實際應用提供理論依據和仿真指導。
用硅基微透鏡作為耦合結構的特點是:①微透鏡尺寸小,可在硅基端直接刻蝕,更易于采用成熟硅工藝進行規模化制備和集成。②硅材料折射率為3.45,因此相比于常規材料透鏡(如SiO2),會將耦合焦距和腰斑位置距離縮短,便于集成;如本文設計的三種透鏡都是將光纖和波導的耦合距離控制在近場范圍內并達到80 %的耦合效率,避免了遠場耦合的對準不確定性和能量的發散損耗。③微透鏡對準容差相比于常規尺寸透鏡耦合要小,尚存在優化空間,這也是高集成度所帶來的必然結果。
2 BPM法計算耦合效率原理
波導與光纖的耦合主要有四部分損耗:傳輸損耗、Fresnel反射損耗、對準偏差損耗、模場失配損耗。當波導結構、耦合位置確定時,可基于BPM算法分析仿真三維波導到光纖的耦合過程,計算耦合效果。
2.1 基礎模場理論
基于Maxwell方程對均勻平面波導(如圖2)進行導模條件分析,可結合邊界條件得到TE、TM模式本征方程和標量亥姆霍茲方程:
(1)
(2)
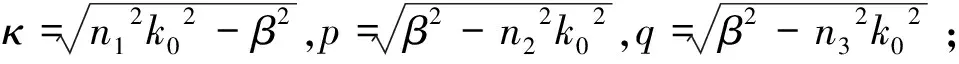
2.2 BPM算法
基于BPM算法可對傳輸路徑每個截面的標量場從二維平面波導(x,z)標量場到三維(x,y,z)進行拓展求解。標量場表示式是按亥姆霍茲方程(2)通過網格離散推導的波動方程(3),截面網格如圖3所示。
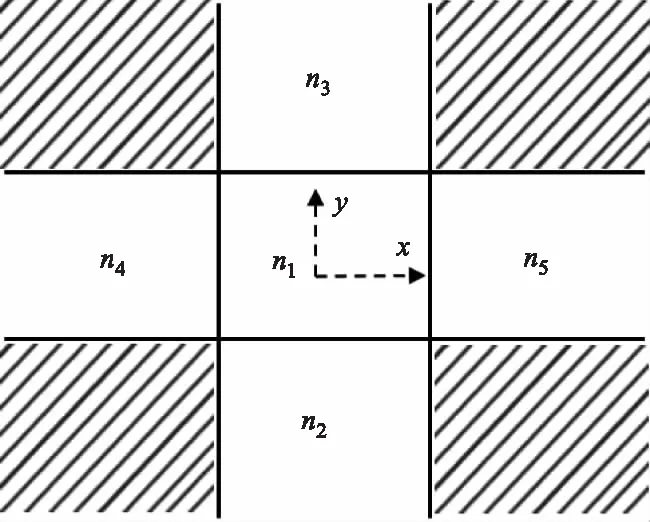
圖3 三維波導截面網格
(3)
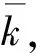
φ(x,y,z)=u(x,y,z)exp(-ikz)
(4)
(5)
通過給定輸入場u(x,y,z=0),迭代求解出z>0方向的場的演化過程。對于波動方程的矢量推導[15-17]即表示場的橫向分量(Ex和Ey),相應的緩慢變化場(ux和uy)滿足如下耦合方程組:
(6)
其中,Ψij是復微分算子:
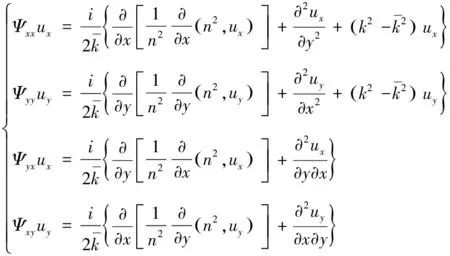
(7)
方程(7)為全向量的BPM方程,對于TE、TM模式,算子Ψxx和Ψyy考慮了界面上不同邊界條件引起的偏振依賴性,并且描述了不同的傳播常數、場形狀、彎曲損耗等對運算結果的影響。算子Ψxx和Ψyy解釋了幾何效應引起的極化耦合和模式混合。另外,Ψxx=Ψyy=0為半向量的近似條件,此時橫向場分量是解耦的,這樣在簡化計算的同時保留了其偏振特性。
根據重疊積分算法可計算出對準模式下空間某點的模式匹配效率:
(8)
除了模式匹配損耗,還需要存在Fresnel反射損耗,根據Fresnel公式計算該耦合結構的端面反射損耗:
(9)
Rloss=-10 lg(R)
(10)
經Zemax軟件對透過率計算,使用硅透鏡于空氣中和單模光纖耦合,1550 nm波長下將有~53.2%的Fresnel反射損耗,該損耗可以通過在耦合端面鍍抗反射(AR)膜來改善,如在SOI端面鍍SiNxOy∶H膜層,單模光纖端面鍍氟化鎂(MgF2)膜層,以實現反射損耗的抑制。目前,這些AR膜在光通信窗口的實際透過效果可達99 %以上[18-19]。因此,下一節的仿真結果已對這部分反射損耗予以補償計算,不再討論未鍍膜情況。
3 結構設計
3.1 波導、光纖建模
按照SOI脊型波導的單模工作條件(γ>0.5)進行建模[13,14,20],如圖4所示,設置脊型波導內脊寬度、厚度:w=h=3 μm,外脊厚度:d=0.6h=1.8 μm;SiO2層、硅基底厚度均大于1.5 μm。單模光纖設置纖芯:折射率n1=1.468 μm、芯徑r1=8.6 μm;包層:折射率n2=1.456、直徑r2=125 μm。背景折射率設為n=1。
在Rsoft軟件中用1550 nm波長光源計算光纖和波導的基模(TE:Ex、Hy),設計結構(圖4)中3 μm脊形波導和芯徑8.6 μm的標準基模Ex分布如圖5所示。
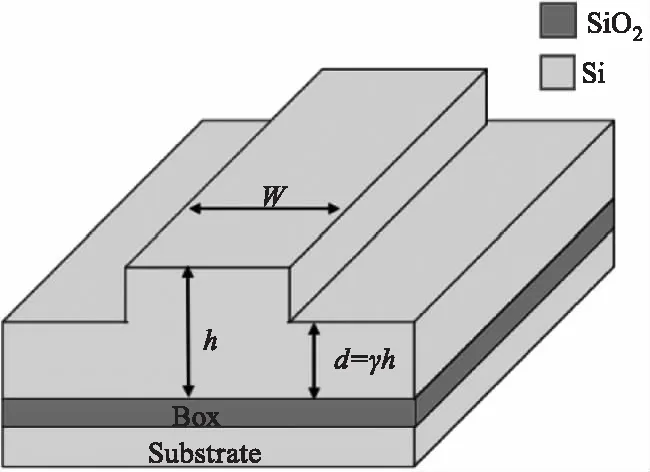
圖4 脊型SOI波導[15]

(a)脊形波導
實際在三維矩形波導中,并不能得到標準的TEM模式,而是在傳輸方向有微小分量的準TEM模式。由于光纖為圓柱波導,波導的光場受橫向限制,故光纖的標準基模為高斯圓斑,模場能量近似高斯分布,不旋轉對稱,因此硅波導和單模光纖中兩個模場的初始形狀、尺寸匹配度并不高,需要在中間加入耦合匹配結構。
3.2 微透鏡設計
使用微透鏡完成波導模場和光纖模場的有效匹配,邊緣耦合是一種可行的集成方式。首先,需要注意的是射線光學中的數值孔徑NA可計算多模光纖的最大入射角度和導模條件,但對于單模光纖的發散角估算是不準確的,單模光纖芯徑一般不超過10 μm,纖芯中僅存在近似0度入射的最低階導模。所以,單模光纖耦合應該著重考慮光纖的模場直徑(MFD)和該過程中高斯光束的傳輸特性[21-22],不應將出射光源簡單地當作點光源處理。高斯光束經透鏡耦合前后的波束變化如圖6所示,可以根據式(11)、(12)設計透鏡參數:
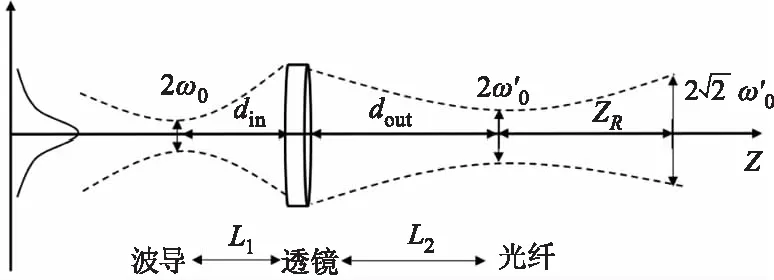
圖6 高斯光束經透鏡耦合
(11)
(12)
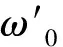
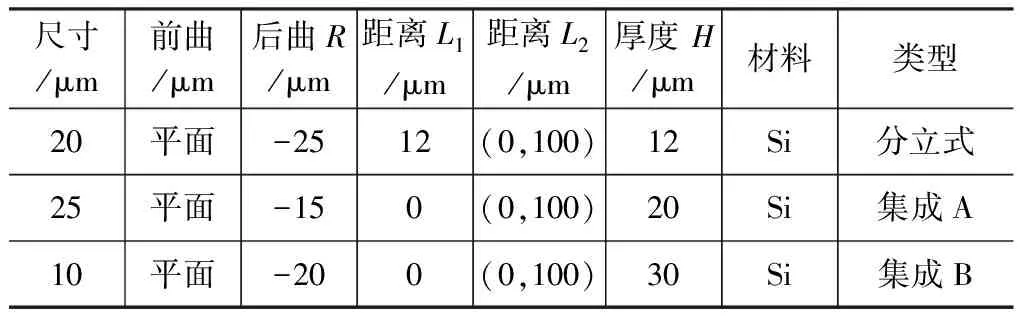
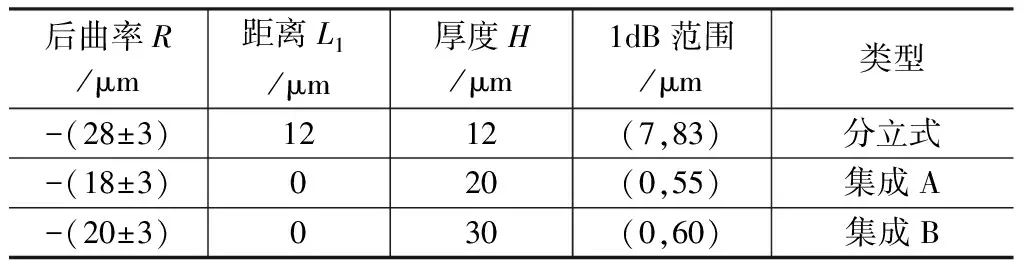
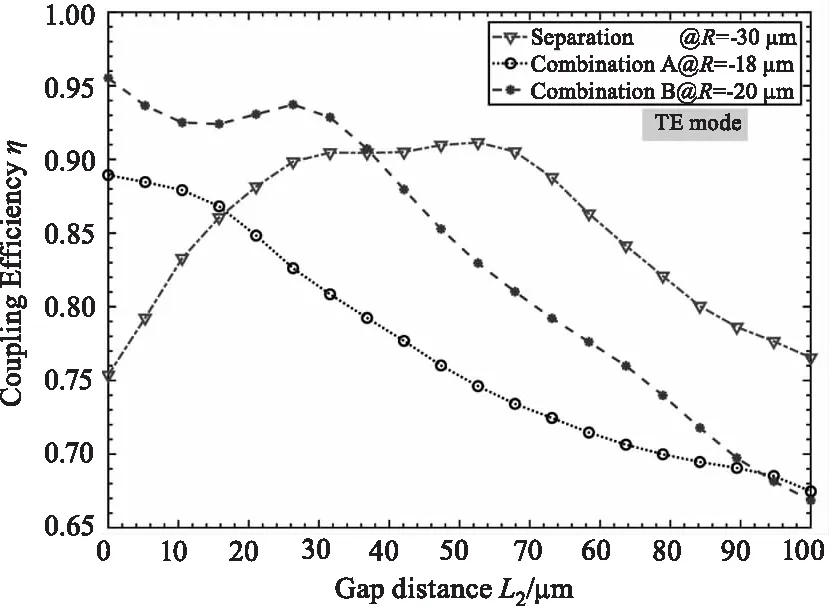
假設波導出射束腰直徑約為3~4.5 μm的標準高斯光束,基于高斯光束傳播理論,若要與模場直徑9~10 μm光纖耦合,則透鏡焦距需要近似滿足13.6 μm 本文研究了與硅波導分立式與硅波導集成式的透鏡結構設計,表1為初始設計參數,圖7為時域有限差分法(FDTD)仿真的在空間尺寸3 μm且波長為1550 nm的高斯光源下三種微透鏡前后腰斑尺寸和位置關系。其中分立式透鏡前曲面距波導端面距離為L1,兩種集成式透鏡(A、B)直接與波導端面貼合即L1=0。 圖7 三種微透鏡前后腰斑-空間位置關系及耦合示意圖 表1 透鏡典型設計參數 采用BPM方法仿真計算了在激勵基模模式下沿Z方向的脊波導和單模光纖纖芯中的光場分布,仿真區域值設置為(30,30,z):硅波導正Z向出射波長1550 nm光束經過微透鏡改變光束傳播途徑以限制光束入纖角度,并進行一定程度的模斑轉換,經空間傳播后入射纖芯,如圖7(d)所示。由于光在空間中傳輸了一段距離,因此入射纖芯的模場并不是穩定的場,包含了導模和輻射模,只有滿足纖芯導模條件的成分會被耦合入光纖繼續傳播,并被監視器計算耦合光場(入纖長度為200 μm)的重疊積分。 波導出射并不是高斯圓斑,雖然在不同位置的光場切片可以觀察到微透鏡也能進行一定程度上的模斑轉換,但是腰斑位置和光束的發散特性與理論設計仍會有一定偏差。通過對表1設計的三種透鏡通過仿真掃描后曲率R、端面-光纖距離L2與耦合效率η的關系可得到在1550 nm波長單模1 dB耦合損耗的最佳曲率參數,見表2。 表2 1550 nm單模條件最佳耦合參數 圖8選取了三種參數對透鏡與光纖端面距離L2對耦合效率的影響進行了計算掃描,可見分立式結構的1 dB耦合距離是較長的,此結構分立距離為12 μm。兩種集成透鏡(A、B)更適宜近場耦合,經仿真分析,這三種透鏡在100 μm范圍內可以實現68 %以上的耦合效率,且TE/TM耦合結果顯示三種結構都存在有一定偏振模式差異,譬如R=-30 μm分立式透鏡偏振差異約2.4 %,R=-18 μm集成式A透鏡的偏振差異約5 %,R=-20 μm集成式B透鏡存在1.8 %的偏振差異。另外,在耦合中也會存在端面錯位造成的損耗,通過在在空間設置光纖和波導錯位參數,可研究三種透鏡在端面平行對準情況下的錯位損耗容限。 (a)TE模 對光纖基于不同透鏡與波導對準耦合時(與Z向平行)可能出現的橫向偏移量δx、縱向偏移量δy對耦合效率(TE模式)的影響分析結果如圖9所示。因為波導出射模斑在y軸方向的模式尺寸較小,三種透鏡在(x,y)截面y方向的偏移更加敏感,所設計的三種透鏡在整體結構橫縱偏移量在<1.5 μm時可有80%以上的耦合效率。 本文通過初步設計仿真證明,基于高斯光束傳播理論設計的波導邊緣集成的硅基微透鏡用于硅波導到單模光纖的光學耦合是可行的,在保證對準精度的情況下在近場可有~90%的耦合效率。這種耦合結構可作為硅波導集成器件與單模光纖進行近距離光學互連的一種普遍手段,如陣列波導光柵(AWG)芯片出射波導與光纖的耦合,為硅光子器件的耦合與集成化研究提供了新的研究方法。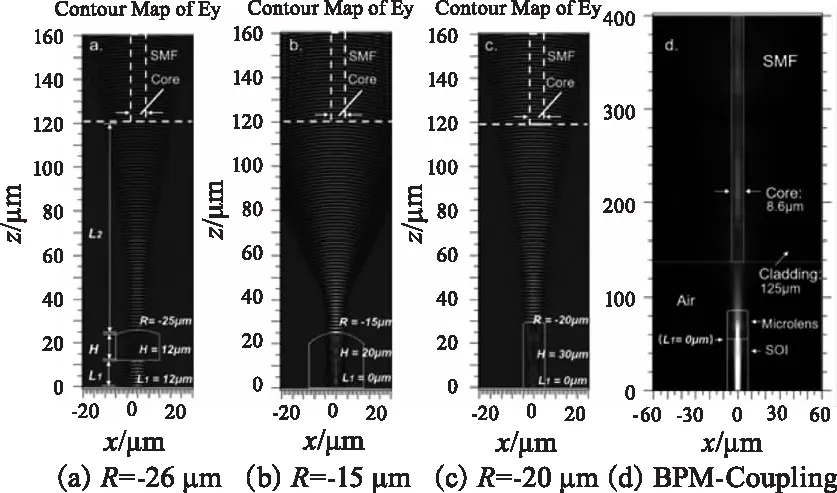
4 仿真分析
5 總 結

