非相干疊加光束攜帶C點偶極子的演化特性

陳海濤，李 婷，高曾輝

(1.成都師范學院 物理與工程技術學院，成都 611130；2.宜賓學院 計算物理四川省高校重點實驗室，宜賓 610064)

引 言

奇點光學主要對光場中出現的位相奇點或者偏振奇點進行研究，由于其在光操縱、原子捕獲光干涉度量和顯微檢測等方面日益重要的應用而成為現代光學的一個重要分支。典型的位相奇點包括螺旋型位錯(光渦旋)和刃型位錯兩種，而光渦旋偶極子被定義為帶有相反拓撲電荷的一對光渦旋[1]。INDEBETOUW研究發現,構成光渦旋偶極子的兩個光渦旋，因帶有相反拓撲電荷而在空間傳輸中相互吸引并湮滅[1]。FREUND的研究表明：傳輸過程中湮滅的光渦旋偶極子會在光傳輸過程中在遠場重現[2]。ROUX采用旁軸近似理論，分別討論了光渦旋偶極子在自由空間和梯度折射率介質的傳輸軌跡[3-4]。Lü等人研究了光渦旋偶極子通過像散透鏡和半屏衍射的演化特性[5-6]。

矢量光束中存在的典型偏振奇點有兩種:一是光場中孤立的圓偏振點，定義為C點，從C點起偏振橢圓退化為圓；二是L線，線上點的偏振橢圓退化為線[7]。實驗上可以采用干涉或者衍射的方法，兩束非均勻光束進行疊加來產生C點[8-10]。此外,偏振奇點也可以由兩束單色光束非相干疊加產生[11-12]。類似于光渦旋偶極子的定義。FREUND將C點偶極子定義為具有對稱性并帶相反指數IC為+1/2和-1/2的一對C點，通過相干疊加的方法在光束束腰處嵌入預期的奇點結構，來浮現C點偶極子[10]。跟光束相干的相干疊加相比，激光束非相干疊加對其相位和偏振沒有嚴格要求，不需要控制光束的相位，結構簡單而易于實現[13]。

穩定激光腔輸出的光束屬于各類高斯光束，而非穩腔輸出的基模光束準直后的遠場光強度分布接近高斯分布，因此，高斯光束傳輸的研究在理論和在工程實踐中都有重要意義[14]。多數奇點光學的研究基于光束傳輸的旁軸近似理論對奇點的空間演化特性進行討論。但是，對于擁有大發散角或者跟波長相比擬的小光斑尺寸的光束傳輸，采用旁軸理論得到結果并不準確，光束傳輸的非旁軸效應應該予以考慮[15-18]。因此，作者擬對高斯光束進行非相干疊加得到C點偶極子，對旁軸和非旁軸兩種情形下C點偶極子的演化進行理論分析和數值模擬研究，并將兩種情形的演化特性進行對比。

1 理論計算

1.1 旁軸情形

設初始單色矢量電場E由具有相同角頻率ω的兩束矢量光束E0,A和E0,B非相干疊加構成，它們可以表示為:

(1)

式中,i和j分別表示x方向和y方向的單位矢量，t表示時間變量。

在非相干條件下，總電場的斯托克斯參數為各個非相干成分的斯托克斯參數之和[12]:

Sl=Sl,A+Sl,B，(l=0,1,2,3)

(2)

其中,

(3)

式中，Re和Im表示相應函數的實數和虛數部分，*表示對相應函數取復共軛。

光場中的C點位置可以通過對應的斯托克斯標量場來描述[19]：

S1，2=S1+iS2

(4)

要采用非相干疊加光束在光場中得到C點偶極子，假定初始場成分E0,A和E0,B為：

(5)

式中,w0為光腰半徑,s為離軸距離。將(5)式代入(2)式～(4)式得：

S1,2=(x0+s+iy0)(x0-s-iy0)×

exp[-(x02+y02)/w02]

(6)

(6)式表明,初始平面光場含有奇點指數為±1/2的一對C點偶極子，這兩個C點對稱位于(-s,0)和(s,0)。

在旁軸近似下，采用菲涅耳衍射積分公式，得到平面傳輸距離z>0處的EAx,EAy,EBx和EBy為：

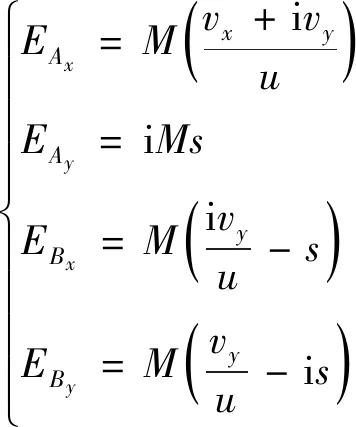
(7)

其中,

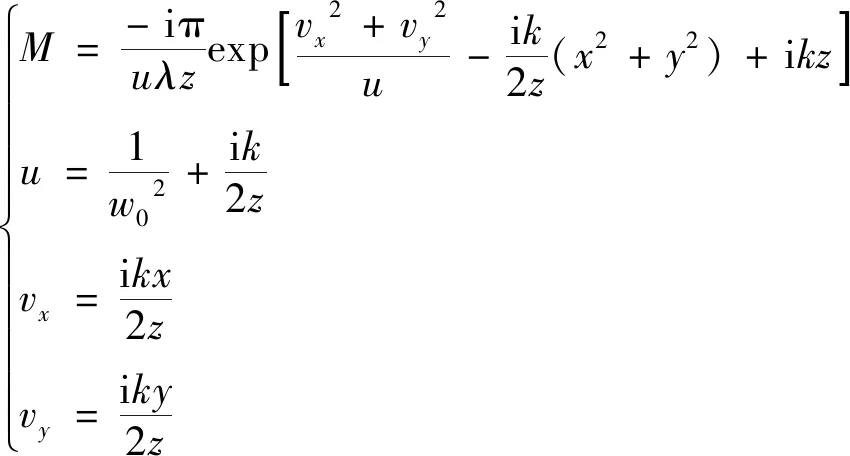
(8)

式中，k為與背景光束波長λ有關的波數，k=2π/λ。

將(7)式和(8)式代入(2)式～(4)式,得到z平面處C點的坐標：

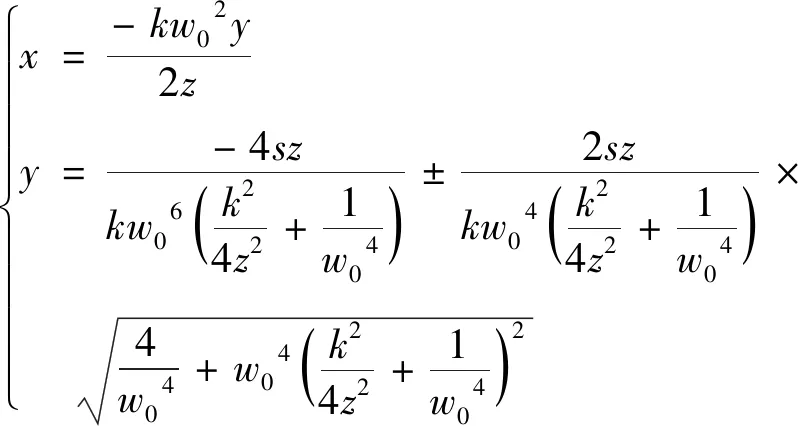
(9)

由(9)式可以看出：在旁軸近似下，雖然攜帶C點偶極子的兩束非相干疊加光束中C點的位置跟傳輸距離z、光束波長λ、光腰半徑w0以及離軸距離s有關，但并沒有出現C點產生和湮滅。這與攜帶C點偶極子的單一高斯光束的傳輸特性不同，后者在傳輸過程中，有新的C點產生和湮滅現象發生[10]。

由(9)式可知，連接這兩個C點的直線斜率可以表示為:

m=2z/(kw02)

(10)

(10)式表明,隨著傳輸距離的增加，連接這兩個C點直線的斜率是單調增加的。

1.2 非旁軸情形

在非旁軸情形下，將(5)式代入瑞利-索末菲衍射積分，得z>0平面處的光場為：

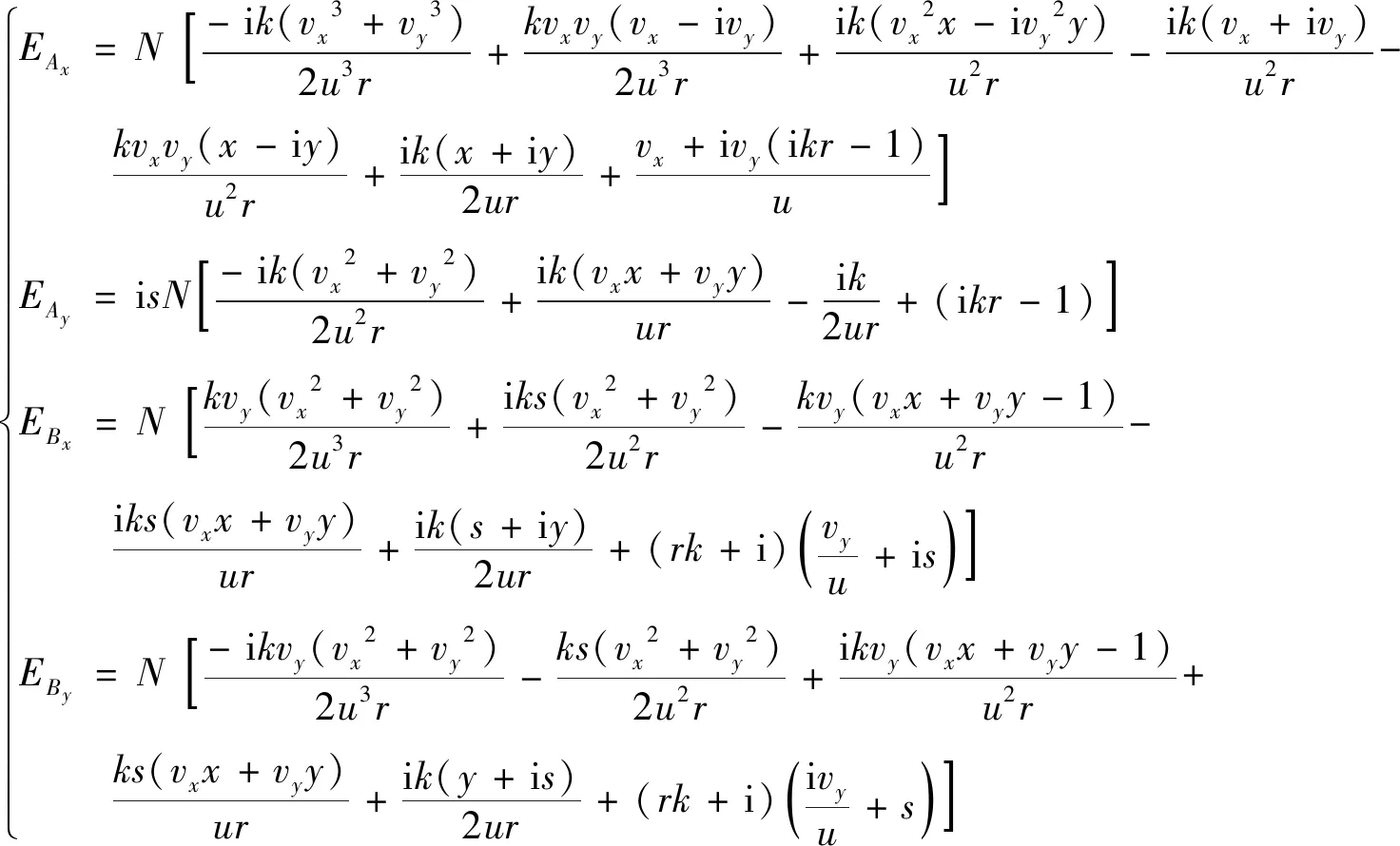
(11)

式中,

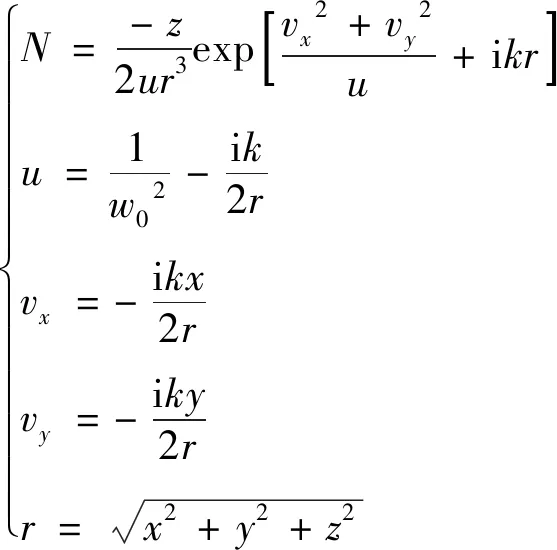
(12)

比較(7)式和(11)式可以看出，攜帶C點偶極子的光束非旁軸情形下的傳輸表達式比旁軸情形復雜得多，并且也不容易得到光束傳輸過程中的C點位置坐標公式。

2 數值模擬

2.1 旁軸情形

在數值計算時，C點的奇點指數可以根據符號法則來確定[20]，其旋向性由斯托克斯參數S3的正負來判定[21]，偏振度由下式決定[22]:

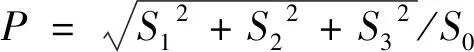
(13)

圖1為旁軸情形下自由空間傳輸的C點偶極子光束的S1,2的等位相線圖。其中計算參數λ=1050nm,w0=2mm,s=0.2w0,圖中用白色小圓點(黑色小圓點)表示奇點指數為+1/2或-1/2的C點。由圖1a可見，與(6)式一致，初始平面z=0出現了有由奇點指數為±1/2的C點1和2構成的C點偶極子，這兩個C點對稱的位于(-0.4mm,0mm)和(0.4mm,0mm),其旋向性均為+1，偏振度都是1。由傳輸距離增加到z=0.001zR(其中zR=πw02/λ2)的圖1b可見，C點1和2移動到分別到位置(-0.41mm,0.04mm)和(0.41mm,0.04mm)處。雖然，這兩個奇點的旋向性不變，但是它們的偏振度分別變為P=0.008和P=0.97。由圖1a～圖1d可以看出，隨著傳輸距離的增加，連接兩個C點的直線斜率不斷增加，這與(9)式相一致。因此，隨著傳輸距離的增加，由高斯光束非相干疊加形成的C點偶極子的位置和偏振度可能改變，但并沒有新的C點產生。該結論與通過相干高斯光束產生的C點偶極子演化特性不同，后者隨著傳輸距離的增加，會出現C點的產生和湮滅現象[10]。

Fig.1 Contour lines of phase of S1,2 of the paraxial beams carrying a C-dipolea—z=0 b—z=0.1zR c—z=zR d—z=50zR

2.2 非旁軸情形

圖2為非旁軸旁軸情形下自由空間傳輸的C點偶極子光束的S1,2的等位相線圖。為了滿足瑞利衍射積分條件，背景高斯光束成分的光腰半徑取作w0=2μm，其它計算參數與圖1相同。當傳輸距離增加到z=0.01zR(見圖2b)時，C點1和2分別移動到位置(-0.374mm,0.008mm)和(0.161mm,0.003mm)處,它們的偏振度則由P均為1分別變為0.22和0.27。除了C點1和2之外，光場還出現了C點3,4,5和6，它們的奇點指數分別為+1/2,-1/2,+1/2,-1/2，偏振度分別為0.36,0.35,0.36,0.67。當傳輸距離增加到z=0.042zR(見圖2c)，光場中除了C點1～6之外，出現了新的C點7和8，這兩個奇點的奇點指數分別為+1/2和-1/2，偏振度分別為0.65,0.57。在此之后，C點3和4因其奇點指數相反和旋向性相同，隨著傳輸距離的增加而相互靠近，直到z=0.5zR時(見圖2d)最終結合而湮滅。同理，C點2和5在距離傳輸到z=4.9zR時(見圖2e)湮滅，C點2和5在距離傳輸到z=10.39zR時(見圖2f)湮滅。因此，隨著傳輸距離的增加，非旁軸旁軸情形下C點偶極子光束在傳輸過程中出現了多對C點的產生和湮滅。這與旁軸情形C點偶極子光束傳輸特性不同，隨著傳輸距離的增加，旁軸C點偶極子光束中沒出現C點產生的產生和湮滅現象。

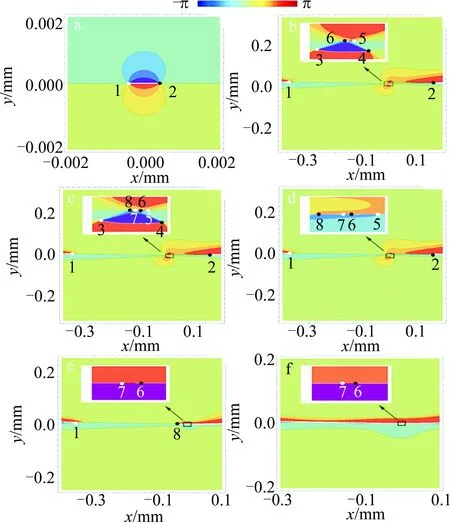
Fig.2 Contour lines of phase of S1,2 of the nonparaxial beams carrying a C-dipolea—z=0 b—z=0.01zR c—z=0.042zR d—z=0.5zR e—z=4.9zR f—z=10.39zR

圖3是位置z=zR處C點偶極子非旁軸光束的S1,2隨其光腰半徑w0變化的等位相線圖。其它的計算參數跟圖2相同。由w0=0.1μm(見圖3a)可以看出，C點1,2,3和4出現在光場中，它們的奇點指數分別為+1/2,-1/2,+1/2,-1/2，偏振度分別為0.968,0.968,0.342,0.168。隨著w0增加，C點3和4因帶相反的奇點指數相互吸引而靠近(見圖3b)。在w0增加到0.222μm(見圖3c)時，C點3和4湮滅。但當w0

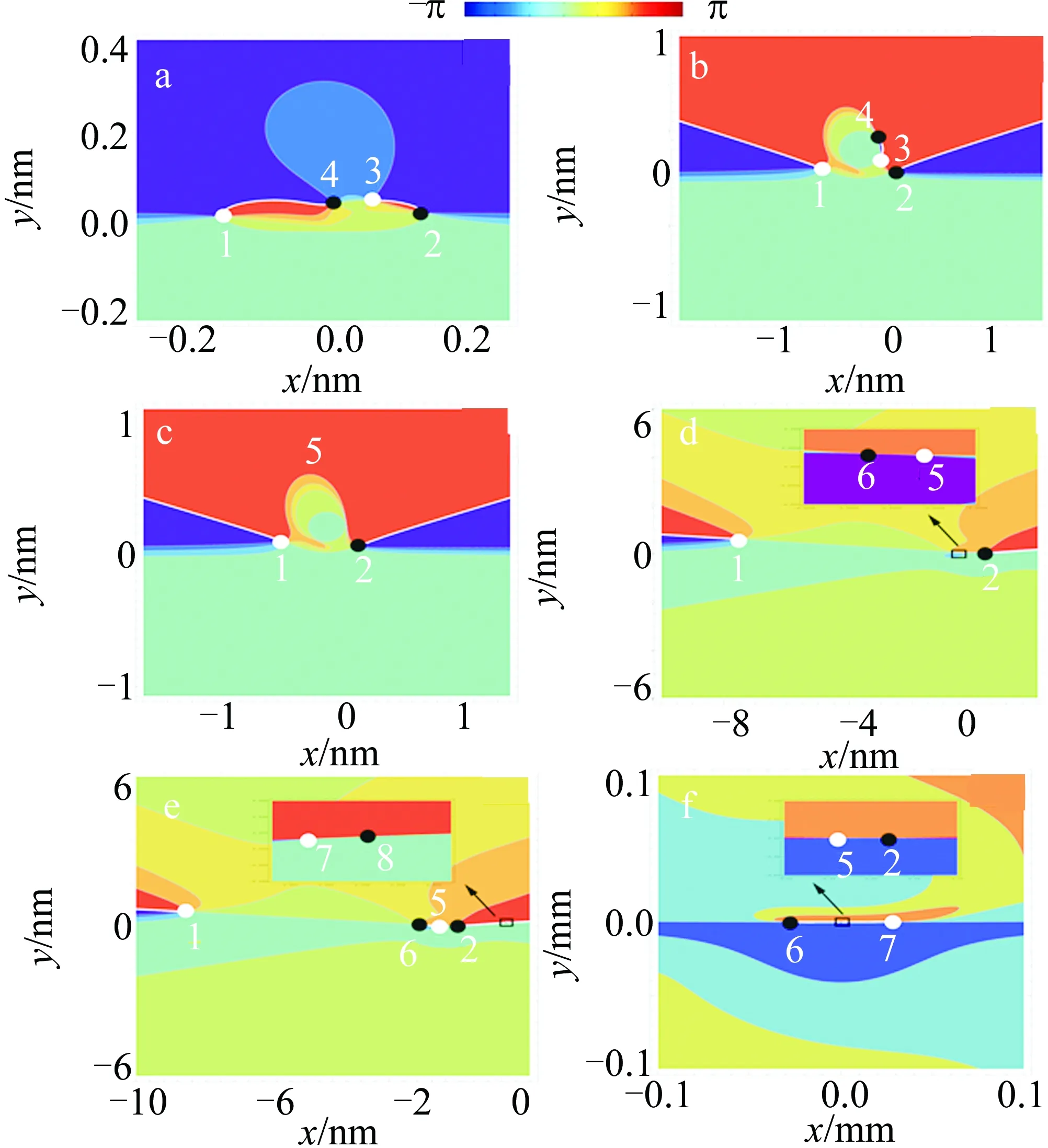
Fig.3 Contour lines of phase of S1,2 for different waist widths of the host beamsa—w0=0.1μm b—w0=0.221μm c—w0=0.222μm d—w0=0.56μm e—w0=0.597μm f—w0=6.2μm

增加到0.56μm(見圖3d)時，光場出現了一對新的C點5和6，它們帶有相反奇點指數+1/2和-1/2，相同偏振度0.75。當w0增加到0.597μm(見圖3e)時，光場又出現了帶有相反奇點指數+1/2和-1/2，相同偏振度0.27的一對C點7和8。此后，隨著w0增加，C點1和8因帶有相反拓撲電荷和相同偏振度而彼此靠近而湮滅(見圖3f)。因此，隨著光腰半徑的變化，有帶有相反拓撲電荷和相同偏振度的成對C點產生和湮滅現象發生。這與旁軸情形C點偶極子演化特性不同，由旁軸情形z平面處光場C點坐標(9)式可以看出，旁軸C點偶極子光束中C點的個數不隨光腰半徑的改變而改變。

圖4為非旁軸光束的S1,2隨離軸距離s變化的等位相線圖。其它計算參數跟圖2相同。由s=0w0(見圖4a)可以看出，只有奇點指數為-1/2和偏振度為1的C點1出現在光場中。但是，當離軸距離s增加到0.023w0(見圖4b)時,除了C點1之外，奇點指數為+1/2和偏振度為1的C點2也出現在光場中。當離軸距離s增加到 0.044w0(見圖4c)時,光場中產生一對新的C點偶極子3和4，它們的奇點指數為-1/2和+1/2，偏振度均為1。當離軸距離s增加到 0.05w0(見圖4d)時,光場中又出現一對C點偶極子5和6，它們的奇點指數為-1/2和+1/2，偏振度均為1。隨著離軸距離s增加，C點1和4因帶有相反拓撲電荷和相同偏振度而彼此靠近而湮滅。這說明：隨著離軸距離的變化，非旁軸光束中不僅出現成對C點的產生和湮滅，也有單個C點的產生。該結論與通過相干高斯光束產生的C點偶極子演化特性不同，后者沒有單個C點的產生或湮滅[10]。這與旁軸情形C點偶極子演化特性不同，由旁軸情形z平面處光場C點坐標(9)式可以看出，旁軸C點偶極子光束中C點的個數不隨參數離軸距離的改變而改變。

Fig.4 Contour lines of phase of S1，2 for different off-axis parametera—s=0.01w0 b—s=0.023w0 c—s=0.044w0 d—s=0.05w0 e—s=0.72w0 f—s=0.73w0

圖5為非旁軸光束的S1，2隨波長λ變化的等位相線圖。其它的計算參數跟圖2相同。在波長λ=0.193μm(見圖5a)時，C點1,2,3和4出現在光場中，它們的奇點指數分別為+1/2,-1/2,+1/2和-1/2，偏振度分別為0.96,0.68,1和1。當波長λ增加到1.55μm(見圖5b)時，在C點3和4之間出現了一對新的C點，它們的奇點指數分別為+1/2和-1/2，偏振度均為1。因此，隨著背景光束波長λ的變化，除了C點的位置和偏振度改變外，還有成對的C點產生。這與旁軸情形C點偶極子演化特性不同，由旁軸情形z平面處光場C點坐標(9)式可以看出，旁軸C點偶極子光束中C點的個數不隨背景光束波長的改變而改變。

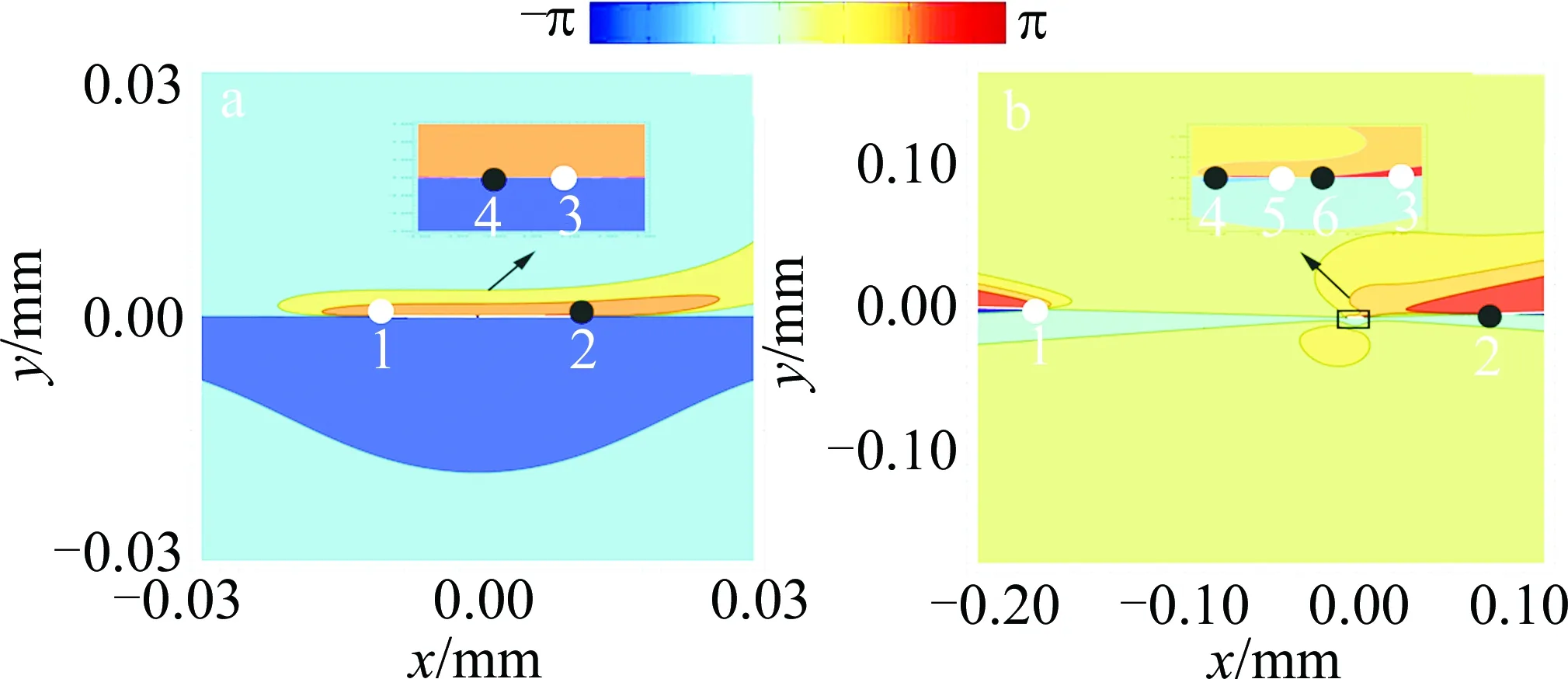
Fig.5 Contour lines of phase of S1，2 for different wavelengths of the host beamsa—λ=0.193μm b—λ=1.55μm

3 結 論

通過兩束矢量高斯光束的非相干疊加得到了C點偶極子，然后從理論上和數值模擬討論了旁軸和非旁軸情形下C點偶極子光束的演化特性。研究表明：在旁軸情形下，構成該C點偶極子的C點的位置和偏振度跟光束傳輸距離、離軸距離和背景光波長有關，連接C點偶極子的軸線斜率隨傳輸距離的增加而單調增加。在非旁軸情形下，當傳輸距離、離軸距離和背景光束波長變化時，除了C點位置和偏振度可能變化外，還有成對的C點因帶有相反奇點指數而接近和湮滅.這些結果與旁軸矢量光束情形類似。但是對于非旁軸情形，光束在傳輸過程中，光場中出現更多C點，有新的單個C點或者C點偶極子產生。這與旁軸情形C點偶極子演化特性不同，當傳輸距離、光束波長、光腰半徑和離軸距離等參數改變時，旁軸C點偶極子光束中并沒出現C點產生的產生和湮滅現象。

非旁軸情形下C點偶極子光束演化特性比旁軸情形豐富和復雜的原因在于,旁軸情形和非旁軸情形C點偶極子光束的傳輸遵從不同的傳輸規律：旁軸光束傳輸遵從菲涅耳衍射積分公式,而非旁軸光束傳輸遵從瑞利-索末菲衍射積分。盡管兩種情形的入射C點偶極子光束完全相同，但是兩種情形的z>0平面的光場表達式完全不同，非旁軸情形的表達式要復雜得多。這說明非旁軸情形下C點偶極子光束的演化特性比旁軸情形顯得更豐富和復雜。研究結果對于深入理解非旁軸矢量光束奇點光學和尋找奇點光學的潛在的應用具有參考價值。