基于EKF和模態(tài)坐標轉(zhuǎn)換的結(jié)構(gòu)損傷識別方法
戴 霖
(江西省水利科學院,江西 南昌 330029)
0 引言
擴展卡爾曼濾波(extended kalman filter,EKF)是在線性最小方差估計的基礎上,提出的一種實時遞推型的最優(yōu)估計濾波算法,近年來被逐步應用于工程結(jié)構(gòu)的參數(shù)識別研究[1-5]當中。為解決傳統(tǒng)EKF算法中其狀態(tài)向量維度過大導致該算法運行效率變慢、識別精度下降等問題,本文提出了一種改進的EKF算法,引入模態(tài)坐標變換,利用模態(tài)坐標轉(zhuǎn)換對傳統(tǒng)EKF的狀態(tài)向量進行處理,構(gòu)建以模態(tài)坐標初始值和結(jié)構(gòu)損傷參數(shù)的狀態(tài)向量。由于結(jié)構(gòu)振動響應通常由前幾階的低階頻率成分組成,因此,對復雜結(jié)構(gòu)可以有效縮減狀態(tài)向量的維數(shù),以保證算法的穩(wěn)定性及準確性。
本文運用該算法對一多自由度系統(tǒng)的結(jié)構(gòu)參數(shù)進行識別,并采用MATLAB軟件編制了程序。數(shù)值算例的結(jié)果表明,該算法可以對結(jié)構(gòu)的損傷參數(shù)進行識別,且識別效果較好。
1 基本理論
多自由度系統(tǒng)自由振動運動方程:

式中:M,C,K分別為結(jié)構(gòu)質(zhì)量、剛度矩陣;p為各節(jié)點位移向量。
在上式中引入模態(tài)坐標變換p=Φq。式中:q為模態(tài)坐標,Φ為正規(guī)化模態(tài)矩陣,滿足ΦTMΦ=I、ΦTKΦ=Λ[Λ=diag(ω21…ω2n),ωn為結(jié)構(gòu)第n階無阻尼固有頻率]。可將上式模態(tài)坐標進行轉(zhuǎn)化,其運動方程為:
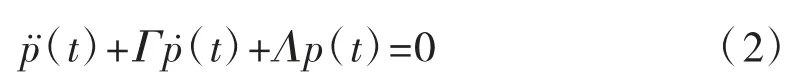
式中:Γ=ΦTCΦ,定義阻尼比ξn=Cn/(2ωnMn),則當0<ξn<1,即在小阻尼情況下,該方程模態(tài)坐標可表示為:


根據(jù)狀態(tài)方程和量測方程,直接套用擴展卡爾曼濾波算法,經(jīng)化簡后其遞推公式為:狀態(tài)預測方程:

式中:Hj為非線性函數(shù)h(θ,x,t)的雅克比矩陣;

當結(jié)構(gòu)質(zhì)量不變,上式計算中所需的?ωn/?αi、?φn/?αi(即固有頻率和模態(tài)關于損傷參數(shù)的靈敏度)可用基準有限元模型計算[6]。
由上述多自由度體系的公式推導中可以看出,將模態(tài)轉(zhuǎn)換理論應用在擴展卡爾曼濾波中,利用模態(tài)坐標轉(zhuǎn)換對傳統(tǒng)EKF的狀態(tài)向量進行處理,構(gòu)建以模態(tài)坐標初始值和結(jié)構(gòu)損傷參數(shù)的狀態(tài)向量后,對于復雜結(jié)構(gòu),可以選取相應的模態(tài)階數(shù)進行計算,達到縮減狀態(tài)向量維數(shù)的效果,從而保證本文改進算法的穩(wěn)定性。
2 數(shù)值算例分析
為利用上述方法來驗證改進的EKF算法在結(jié)構(gòu)參數(shù)識別上的實用性,本文以一個三自由度彈簧質(zhì)點結(jié)構(gòu)模型為例(見圖1)進行驗證。
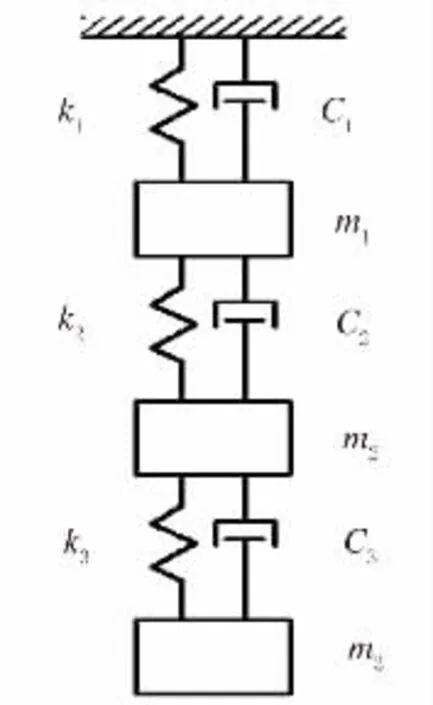
圖1 彈簧質(zhì)點結(jié)構(gòu)模型
本文數(shù)值仿真算例中的各單位采用無量綱化進行處理[7]。三自由度彈簧質(zhì)點結(jié)構(gòu)模型參數(shù)為:彈簧質(zhì)點質(zhì)量m1、m2、m3均為5;彈簧原始剛度k01、k02、k03均為200;彈簧原始阻尼比ζ1、ζ2、ζ3均為0.03;根據(jù)式(4)、式(5),假定彈簧質(zhì)點結(jié)構(gòu)模型損傷后各彈簧剛度損傷因子α1、α2、α3分別為0.9、0.8、0.7;各彈簧阻尼比損傷因子β1、β2、β3分別為1.1、1.15、1.2。
本文通過MATLAB軟件進行計算,在初始條件下,提取自由振動下各個彈簧質(zhì)點的位移響應信號作為觀測值,并同時加入高斯白噪聲模擬觀測噪聲的影響,對結(jié)構(gòu)響應數(shù)據(jù)中無噪聲、5%噪聲和15%噪聲3種情況分別給出識別結(jié)果。
(1)無噪聲下識別結(jié)果見圖2、圖3。
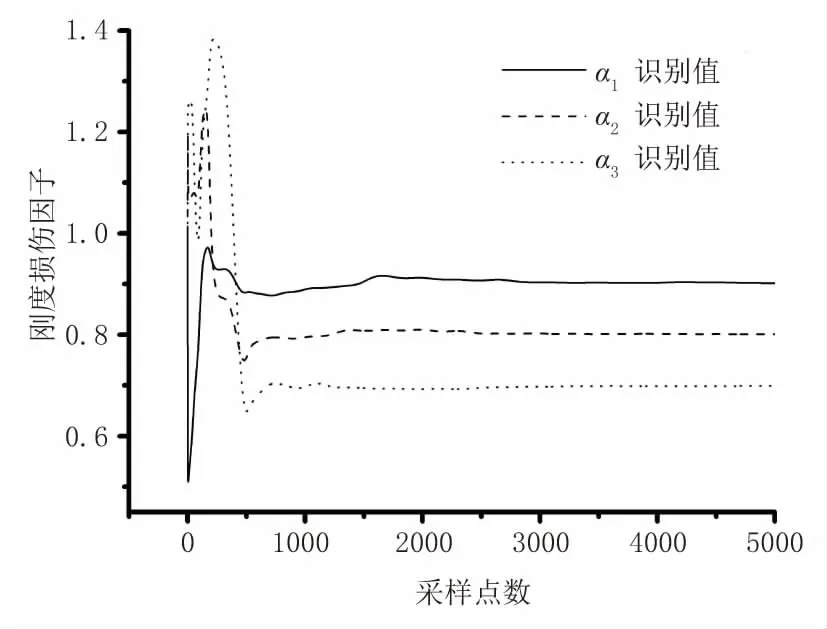
圖2 剛度損傷參數(shù)收斂曲線(無噪聲)
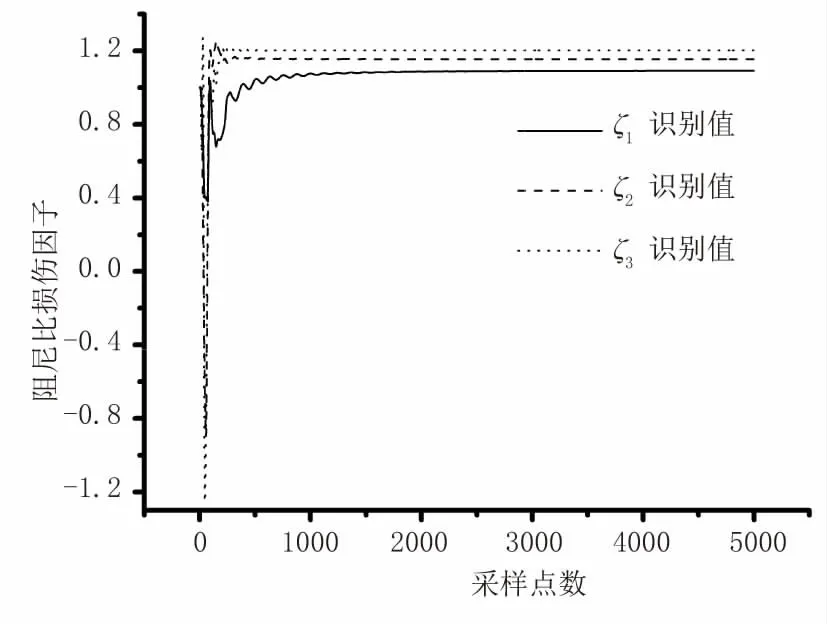
圖3 阻尼比損傷參數(shù)收斂曲線(無噪聲)
(2)5%噪聲下識別結(jié)果見圖4、圖5。

圖4 剛度損傷參數(shù)收斂曲線(5%噪聲)
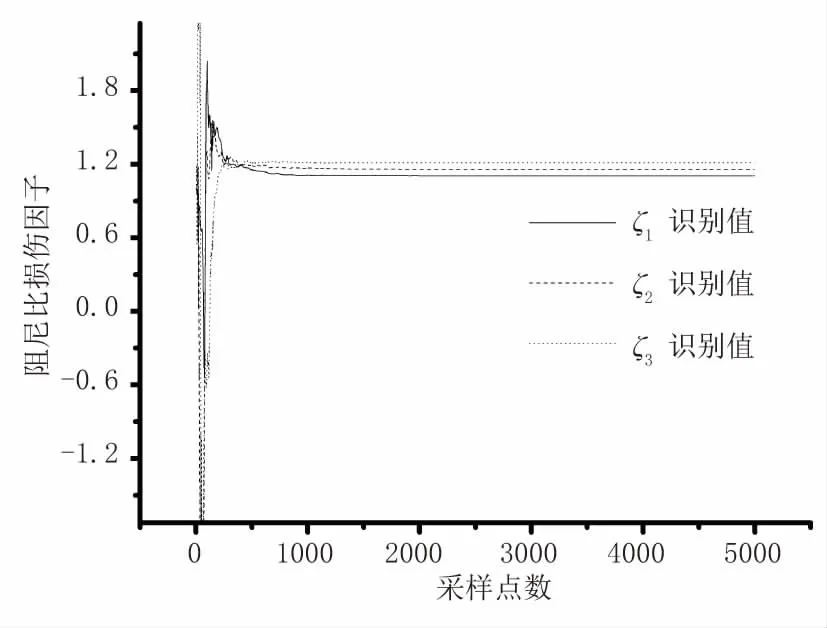
圖5 阻尼比損傷參數(shù)收斂曲線(5%噪聲)
(3)15%噪聲下識別結(jié)果見圖6、圖7。
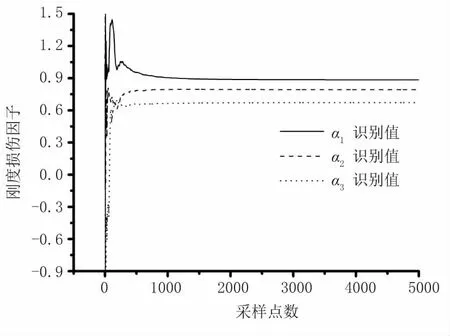
圖6 剛度損傷參數(shù)收斂曲線(15%噪聲)
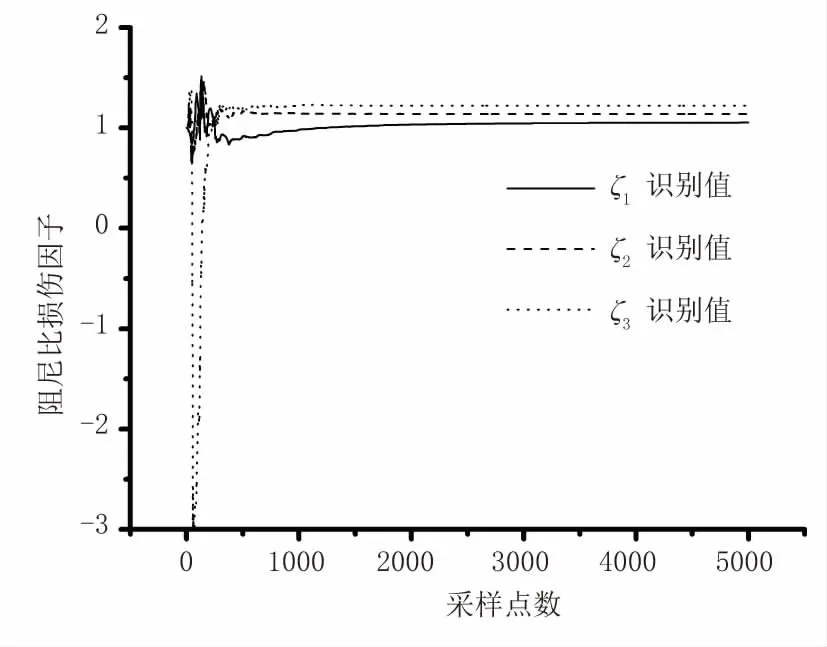
圖7 阻尼比損傷參數(shù)收斂曲線(15%噪聲)
由圖2至圖7結(jié)構(gòu)各損傷因子的收斂曲線可以看出,在不同級別噪聲情況下,各個損傷參數(shù)的識別結(jié)果均可以快速識別,均能夠在短時間內(nèi)收斂且穩(wěn)定趨近于真實值。由表1、表2中結(jié)構(gòu)各損傷因子的識別結(jié)果可以看出,本文改進算法可以對結(jié)構(gòu)損傷后的剛度及阻尼參數(shù)進行識別,且識別效果較好、精度較高。隨著噪聲逐級增加,雖然損傷因子的相對誤差也會相應變大,但是各個參數(shù)識別結(jié)果的精度均較高。表1中,剛度損傷因子識別結(jié)果最大相對誤差為1.71%。表2中,阻尼比損傷因子識別結(jié)果最大相對誤差為3.33%。可見,本文算法具有良好的識別效果。

表1 剛度損傷因子識別結(jié)果
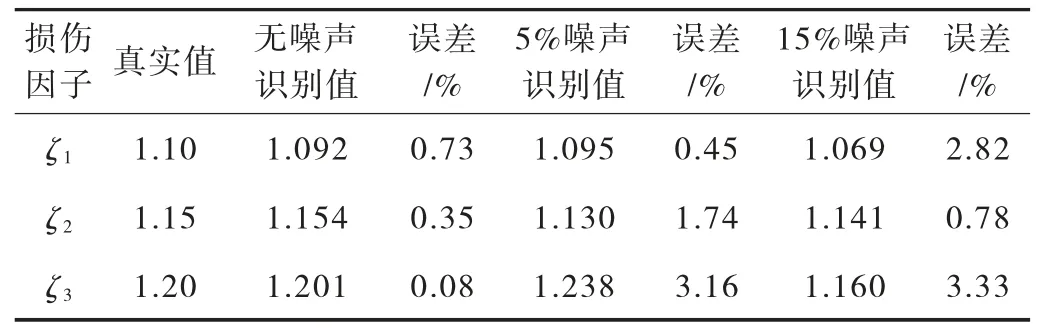
表2 阻尼比損傷因子識別結(jié)果
3 結(jié)論
本文在擴展卡爾曼濾波算法的基礎上,結(jié)合模態(tài)坐標變換,提出了一種改進的擴展卡爾曼濾波算法,并將該算法對一多自由度彈簧質(zhì)點系統(tǒng)進行了數(shù)值算例計算。結(jié)構(gòu)參數(shù)識別結(jié)果表明,該算法可以對結(jié)構(gòu)參數(shù)進行有效識別,精度較高,證明了該算法在結(jié)構(gòu)參數(shù)識別領域當中的可行性。因此,對于復雜結(jié)構(gòu)損傷參數(shù)識別的問題,可以在此基礎上進一步驗證。

