不同動物模型對安格斯牛周歲生長性狀遺傳參數估計的比較分析

馮小芳 蔣秋斐 封 元 王 瑜 母 童 黎 明 陳亞飛 王 影 蔡正云 張 娟 顧亞玲*

(1.寧夏大學 農學院，銀川 750021； 2.寧夏畜牧工作站， 銀川 750001； 3.寧夏海原縣九彩鄉人民政府，寧夏 海原 755200)

周歲生長發育性狀是衡量肉牛經濟價值的一類重要指標，周歲體重和體尺性狀不僅能夠反映出肉牛的生長發育狀況，也能作為判斷小母牛初配時間的依據，因為小母牛初配前較高的周歲體重和良好的體況儲存營養和能量的能力較瘦弱的母牛強，在小母牛排卵期間便可調動這些能量，起到代謝緩沖的作用。肉牛生長發育性狀的選擇是肉牛育種計劃中最重要的一項內容，而準確估計肉牛生長性狀的遺傳參數是科學制定育種方案的前提。

目前，研究肉牛生長發育性狀使用較多的模型是簡單的直接加性遺傳效應模型，因為該模型考慮了全部的親緣關系，估計的殘差方差最小，且該模型估計的遺傳力屬于狹義遺傳力，遺傳具有穩定性，不會隨著世代的增加和環境的變化而大幅度波動。朱波等利用該模型估計了西門塔爾牛初生、6、12、18和24月齡重遺傳力值分別為0.44、0.42、0.35、0.38和0.46；董剛輝等利用此模型估計了三河牛成母牛體重、體高和體斜長等15個生長發育性狀的遺傳參數估計值；周振勇等利用簡單動物模型估計出新疆褐牛各階段體重和體尺性狀屬于中等遺傳力。在肉牛生長性狀的選擇中，除考慮系統環境效應外，同時也應考慮直接加性遺傳效應、母體遺傳效應和永久性環境效應的影響。尤其考慮母體遺傳效應在肉牛選擇中的影響，特別是在直接加性遺傳效應和母體遺傳效應之間存在對立關系的情況下，模型中忽略母體遺傳效應時會導致對總遺傳力的高估。Sanad等估計弗里西亞牛的泌乳期、產奶量和空懷天數等性狀時，認為模型中包含母體遺傳效應及其與個體遺傳效應的協方差比簡單的動物加性效應模型對數據具有更好的擬合效果。Rumph等對海福特牛不同季節性成熟體重進行遺傳參數估計時，認為包括母體遺傳和母體永久性環境效應，以及直接遺傳和直接永久性環境效應的模型最符合遺傳參數估計。Ulutas等從只有直接加性效應的模型到還包括加性母體效應、母體永久環境效應以及直接加性效應和母體加性效應之間的協方差模型獲得威爾士黑牛斷奶前(100 d)和斷奶后(300 d)體重的遺傳力估計值，根據似然比檢驗發現100 d體重最合適的模型是具有直接加性效應和母體加性效應的模型，300 d體重只有直接加性效應的模型是最合適的。Kamprasert等用單變量和多變量的4種動物模型對婆羅門牛出生、200、400和600 d生長發育性狀進行方差組分估計，發現斷奶前性狀受母畜遺傳和永久環境效應影響，400和600 d性狀最適模型為只有直接加性效應的模型。因此，通過選擇合理的模型是提高遺傳參數估計準確性的重要手段。一般來說，動物模型被認為是廣泛應用的首選模型，該模型能夠充分利用數據集中的所有親緣關系，被分為直接遺傳效應、母體遺傳效應和母體永久環境效應模型。

寧夏地區近年來引進大量的黑安格斯牛，這些牛很快適應了寧夏地區特有的生長環境， 目前安格斯牛已經成為寧夏地區肉牛發展的重要基礎。因此，需要一個合適的育種方案來進行遺傳改良，選擇一種最優的動物模型來估計遺傳參數對于育種改良的遺傳選擇進展是至關重要的一步。本研究采用包括環境效應和遺傳效應在內的6種動物模型估計安格斯牛周歲生長發育性狀的遺傳參數，旨在探討母體效應對各研究性狀的影響，同時通過比較不同模型估計的方差組分和遺傳參數間的差異，篩選出最佳估計模型來提高遺傳參數估計的準確性，有助于寧夏地區安格斯牛育種計劃的進一步實施，以期為寧夏地區安格斯牛核心群選育和制定科學合理的選種選配方案提供理論基礎。

1 材料與方法

1.1 數據收集與整理

本研究收集2014—2020年寧夏地區6個安格斯牛核心群選育場的安格斯牛周歲生產性能測定記錄和系譜資料，其中周歲生產性能測定記錄包括公母牛體重(Body weight, BW)、體高(Body height, BH)、體長(Body length, BL)和胸圍(Chest girth, CG)，對原始數據記錄進行預處理，剔除父號和母號記錄缺失和不準確記錄、表型值異常和在平均值±3倍標準差之外的記錄后，最終得到的數據集包含來自29頭公牛和1 641頭母牛后代的3 065條記錄數據用于遺傳參數估計，數據的具體描述性統計見表1。

表1 安格斯牛周歲生長性狀遺傳參數估計數據描述性統計結果
Table 1 Results of descriptive statistics for data on estimated genetic parameters for growth traits at the age of one year in Angus cattle

性狀Trait數據量Amount of data均值Mean標準差SD變異系數CV最大值Max最小值MinBW3 065307.0155.9318.22419.00201.00 BH3 065114.358.327.28139.0096.00 BL3 065127.5613.6710.71200.00103.00 CG3 065154.5616.9710.98203.00116.00

注：BW：體重；BH：體高；BL：體長；CG：胸圍。下同。

Note: BW： body weight； BH： body height； BL： body length； CG： chest girth. The same below.

1.2 參數估計模型

采用六種單性狀動物模型估計安格斯牛生長性狀的遺傳參數，所有模型都包含直接加性遺傳效應，這是模型1中唯一的隨機效應；模型2包括母體永久環境效應；模型3包括母體遺傳效應；模型4與模型3相同，但直接加性遺傳效應和母體遺傳效應之間存在協方差；模型5包括母體遺傳效應和母體永久環境效應；模型6與模型5相同，但在直接加性遺傳效應和母體遺傳效應之間存在協方差。每個性狀的模型如下：

模型1：

y

=

Xb

+

Z

a

+

e

模型2：

y

=

Xb

+

Z

a

+

Z

c

+

e

模型3：

y

=

Xb

+

Z

a

+

Z

m

+

e

σ

,=0模型4：

y

=

Xb

+

Z

a

+

Z

m

+

e

σ

,≠0模型5：

y

=

Xb

+

Z

a

+

Z

m

+

Z

c

+

e

σ

,=0模型6：

y

=

Xb

+

Z

a

+

Z

m

+

Z

c

+

e

σ

,≠0式中：

y

為各性狀的觀測值向量；

b

為固定效應向量(場年效應：6個飼養場和7個出生年度共14個效應水平；年季效應：7個出生年度和4個季節共計28個效應水平；性別效應：公畜和母畜2個效應水平)；

a

、

m

、

c

和

e

分別為直接加性遺傳效應向量、母體遺傳效應向量、母體永久環境效應向量和殘差效應向量；

X

、

Z

、

Z

和

Z

分別為固定效應、直接加性遺傳效應、母體遺傳效應和母體永久環境效應的結構矩陣。

總遺傳力根據以下公式計算：

式中：為總遺傳力，為直接加性遺傳方差，為母體加性遺傳方差，

σ

,為直接遺傳效應和母體遺傳效應之間的協方差，為母體永久環境方差，為殘差方差，為表型方差。

1.3 固定效應顯著性檢驗

利用SAS 9.2統計分析軟件的GLM過程，分析場-年效應、年-季效應和性別效應對周歲體重(BW)、體高(BH)、體長(BL)和胸圍(CG)的顯著性檢驗，檢驗結果見表2。

1.4 不同模型間的比較方法

評價具有嵌套關系的不同動物模型采用赤池信息準則(AIC)和似然比(LR)檢驗進行遺傳參數估計效果檢驗，從而確定安格斯牛周歲生長性狀遺傳參數估計的最優動物模型。AIC的計算公式為

AIC=2

k

-2ln(

L

)

(1)

式中：

L

為最大似然函數值，

k

為需要估計的參數個數。增加模型中參數個數能夠提高擬合的優度，但易造成過度擬合，所以AIC在獎勵擬合優度(由似然函數評估)的同時會懲罰一個估計參數數量遞增函數。給定數據的一組候選模型中首選模型是AIC值最小的模型。判斷是否可以簡化模型Ⅰ為模型Ⅱ的標準，用似然比檢驗(LRT)：

表2 生長發育性狀固定效應顯著性檢驗結果(值)
Table 2 Results of fixed effects significance tests for growth and developmental traits ( value)

性狀Traits場-年Farm-year年-季Year-season性別GenderBW207.62***42.71***23.30***BH292.15***34.33***5.86**BL142.36***29.28***21.10***CG68.88***50.36***12.90**

Note: ***: <0.000 1; **: <0.01.

[-2ln(

L

|模型Ⅰ)]-[-2ln(

L

|模型Ⅱ)]

(2)

式中：LR為似然比值，

L

模型Ⅰ和

L

模型Ⅱ分別為2個不同模型下的最大似然函數值，模型Ⅰ是模型Ⅱ的子模型，LR近似服從卡方分布，自由度為兩模型估計參數個數之差，然后根據卡方分布臨界值表判斷模型差異是否顯著，如果差異顯著，說明增加的參數對該性狀具有顯著影響，否則沒有。

2 結果與分析

2.1 不同動物模型對安格斯牛生長性狀方差組分的估計

2

.

1

.

1

不同動物模型對周歲體重方差組分和遺傳參數估計不同模型估計的安格斯牛周歲體重方差組分和遺傳參數見表3，在不考慮直接加性遺傳效應與母體遺傳效應間協方差的4個模型中，模型1估計的均高于模型2、3和5，且模型2、3和5估計的相同，均為0.48。在有協方差的模型4和模型6 中，和的估計值增加且兩模型估計的和結果相同，分別為0.77±0.01和0.50±0.05。

c

估計值較低，估計值范圍在0.00±0.01～0.17±0.01。在不同模型中估計結果差別較明顯，其中估計值最大的模型是模型1，為0.59±0.02，最小的模型是考慮了協方差的模型4和模型6，估計值均為0.16±0.06。

2

.

1

.

2

不同動物模型對周歲體高方差組分和遺傳參數估計不同模型估計安格斯牛周歲體高的方差組分和遺傳參數詳見表的估計值范圍在0.42±0.02～的估計值范圍為0.04±0.08～0.51±0.05，其中，和估計結果最大的模型均為考慮了直接加性遺傳效應和母體遺傳效應協方差的模型4和模型6，在不考慮此協方差的其他模型中，模型1估計的高于模型2、3和5。模型2、5和 6估計的

c

均較低，變化范圍為的估計值范圍為0.12±0.05～0.52±0.03，估計結果最大的模型是將動物本身作為唯一隨機效應的模型1，估計值最小的模型是考慮了協方差的模型4和模型6。

2

.

1

.

3

不同動物模型對周歲體長方差組分和遺傳參數估計不同模型估計安格斯牛周歲體長的方差組分和遺傳參數詳見表5，在不考慮直接遺傳效應與母體遺傳效應間協方差的模型1、2、3和5中，和的估計值均相同，為0.20，當考慮此協方差時，的估計值增加，模型4和模型6均增加到0.33±0.04，此時估計值下降，模型4和模型6均減小到0.11，的估計值在不考慮協方差的模型中為零，在考慮協方差的模型中估計值為0.10，考慮了母體永久環境效應的模型中，對和

c

的估計值均為零。

2

.

1

.

4

不同動物模型對周歲胸圍方差組分和遺傳參數估計不同模型估計安格斯牛周歲胸圍的方差組分和遺傳參數詳見表的估計值范圍在0.49±0.02～0.70±0.07，的估計值范圍為0.04±0.01～0.23±0.04，其中，和估計結果最大的模型均為考慮了直接加性遺傳效應和母體遺傳效應協方差的模型4和模型6，在不考慮此協方差的其他模型中，模型1估計的高于模型2、3和5的估計值。模型2、5和6估計的

C

均較低，變化范圍為的估計值范圍為0.32±0.01～0.52±0.03，估計結果最大的模型是將動物本身作為唯一隨機效應的模型1，估計值最小的模型是考慮了協方差的模型4和模型6。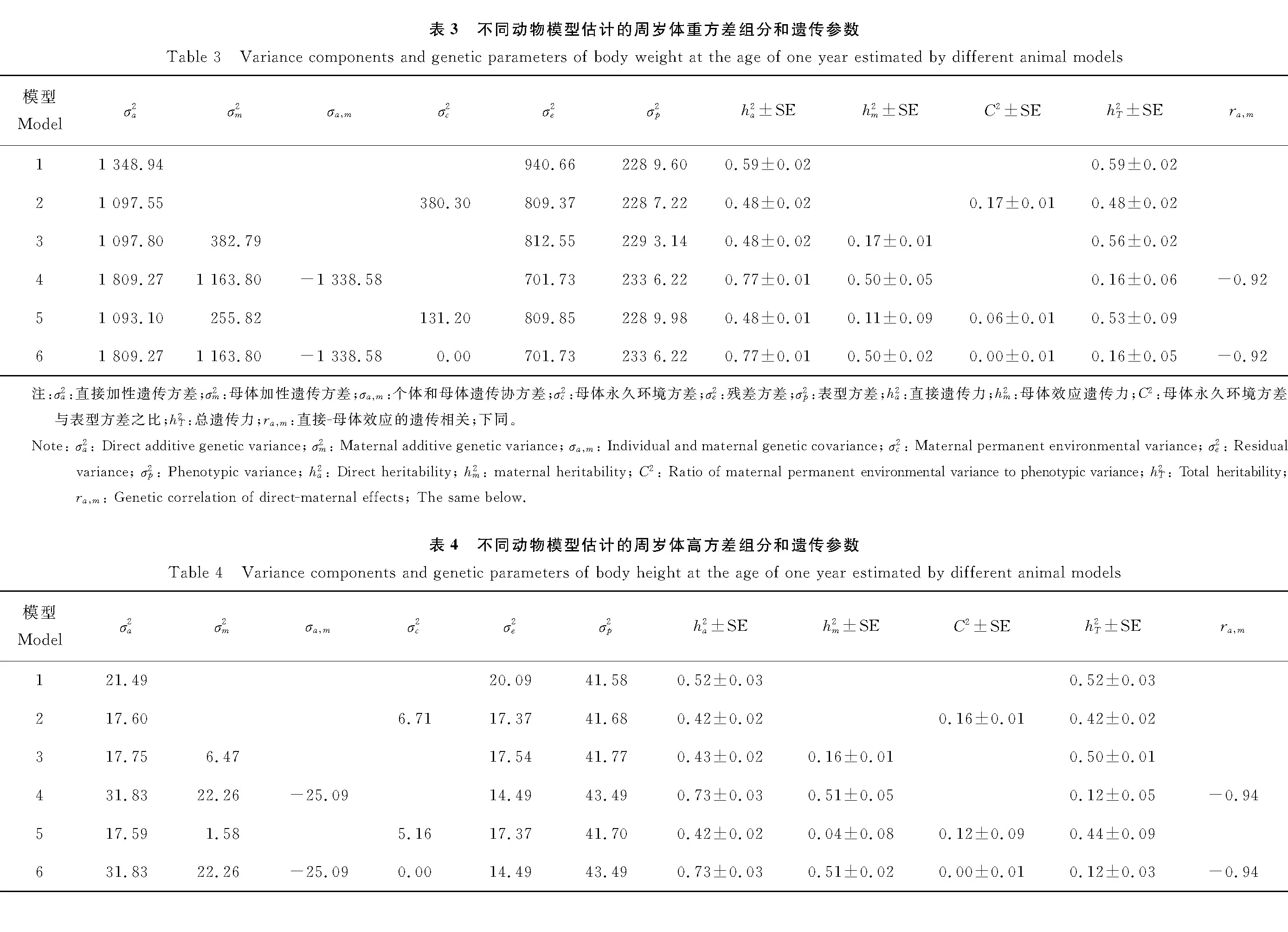

2.2 不同動物模型間的比較

2

.

2

.

1

赤池信息準則(AIC)比較不同動物模型

不同動物模型的-2lnL值和AIC值列于表7，通過比較不同動物模型AIC信息標準值，發現模型4對于安格斯牛周歲體重、體高、體長和胸圍的AIC值均比其他模型低，表明模型4對安格斯牛周歲生長性狀的遺傳參數估計效果最佳。

2

.

2

.

2

似然比檢驗(LRT)比較不同動物模型不同動物模型卡方檢驗結果列于表8，結果顯示，對于周歲體重和體高，模型1與其他模型的卡方檢驗差異極顯著(

P

<0.01)，模型2與模型4和6以及模型3與模型4和6卡方檢驗差異均極顯著(

P

<0.01)，模型2和模型3分別與模型5卡方檢驗差異均不顯著(

P

>0.05)，模型6與模型4的卡方檢驗差異不顯著(

P

>0.05)，與模型5差異極顯著(

P

<0.01)。對于周歲體長和胸圍，模型4和模型6均與模型1、2和3卡方檢驗差異極顯著(

P

<0.01)，模型6與模型5也存在極顯著差異(

P

<0.01)，其余模型間差異均不顯著(

P

>0.05)。

3 討 論

3.1 不同動物模型估計效果的比較

不同遺傳參數估計模型中，隨機效應對安格斯牛周歲體重、體高、體長和胸圍的影響比較相似，母體永久環境效應(模型2)、母體加性遺傳效應(模型3)以及母體永久環境和母體遺傳效應同時相加(模型5)的擬合模型AIC值比較一致，且模型間的卡方檢驗沒有顯著差異(

P

>0.05)，但母體遺傳效應及其與個體直接加性遺傳效應的協方差(模型4)相加時導致AIC值降低，該模型與模型6相比差異不顯著(

P

>0.05)，表明安格斯牛生長性狀遺傳參數估計的最佳模型為模型4，這些性狀受加性遺傳效應和母體遺傳效應及其協方差的影響很大。不同性狀的遺傳力估計值取決于擬合的模型，用模型2、3和5估計的安格斯牛周歲體重、體高和胸圍的個體加性遺傳效應值近似相同，體重的估計值均為0.48，體高的估計值在0.42±0.02～0.43±0.02，胸圍的估計值均為0.49±0.02，但將動物本身作為唯一隨機效應的模型1，比模型2、3和5對個體加性遺傳效應的估計值要高，同樣的，根據模型1，估計不同品種牛體重的遺傳力值也很高。在不考慮個體與母體加性遺傳效應的協方差模型中，周歲體重、體高、體長和胸圍的直接遺傳力和母體效應遺傳力估計值較低，但在有此協方差的模型中，估計值增加。Shokrollahi等利用有協方差的模型估計所研究性狀的遺傳參數時，也出現了估計值增加的情況，認為這可能是由于直接加性遺傳效應與母體遺傳效應之間的負相關所影響。

3.2 不同動物模型對周歲生長性狀遺傳參數的估計

在本研究中，周歲體重的直接遺傳力估計值范圍為0.48±0.01～0.77±0.01，不同群體的安格斯牛周歲體重遺傳力也存在一定差異性，Robinson估計的安格斯牛周歲體重的直接遺傳力0.24；Rafael等和Meyer等估計安格斯牛周歲體重的遺傳力分別為0.27和0.50。本研究周歲體重母體遺傳力范圍為0.11±0.09～0.50±0.05，對周歲體重的影響較大，是否是由于斷奶較遲或母體效應對斷奶應激效應作用的結果有待進一步研究。且周歲體重直接-母體效應的遺傳相關(

r

,)為-0.92，結合Meyer對初生重、斷奶重和周歲重直接-母體效應遺傳相關估計值(分別為0.06、-0.29和-0.65)可以看出母體效應對犢牛的影響可持續到周歲重。其他品種牛周歲重的直接遺傳力和母體遺傳力估計在文獻中也有很多報道，取值范圍也很大，文獻中報道的周歲重遺傳力估計值范圍為0.16～0.73。Pelicioni等估計古澤拉特牛直接遺傳力在0.02～0.16，呈中低值，母體遺傳力估計略高(0.00～0.24)；Diop等估計的戈布拉牛周歲體重的直接遺傳力和母體遺傳力的估計值分別為0.24和0.21；Barros等估計內洛爾黃牛周歲體重直接遺傳力為0.54，母體遺傳力估計值很低，接近于零；Fernando等利用多性狀動物模型分析得到12月齡體重直接遺傳力估計值為0.29，母體遺傳力為0.02；在本研究最佳模型中，周歲體重的直接遺傳力為0.77±0.01，本研究的高遺傳力估計值與Lopes等用貝葉斯方法估計的內洛爾黃牛周歲重遺傳力值接近(0.72)。高于用簡單動物模型估計的泰國婆羅門牛周歲體重遺傳力(0.20±0.02)、比利時藍牛13月齡體重遺傳力(0.51)和內洛爾牛周歲體重遺傳力估計值(0.37±0.03)。由表4～表6可知，安格斯牛周歲體高、體長和胸圍的直接遺傳力分別為0.42±0.02～0.73±0.03、0.20±0.02～0.33±0.04和0.49±0.02～0.70±0.07，母體遺傳力分別為0.04±0.08～0.51±0.05、0.00 ±0.02～0.10±0.04和0.04±0.01～0.23±0.04。在其他肉牛品種中，對體高、體長和胸圍的遺傳力估計也有相關報道，汪聰勇等估計了夏南牛周歲體高、體長和胸圍的遺傳力估計值分別為0.57、0.49和0.39。周桂珍等估計西門塔爾牛體高、體長和胸圍的遺傳力估計值分別為0.67、0.67和0.56。Kamprasert等估計出婆羅門牛400日齡體長和胸圍的遺傳力估計值分別為0.48和0.36。Supriyantono等估計的周歲巴厘牛體高、體長和胸圍的遺傳力估計值分別為0.41、0.38和0.40。本研究和其他學者研究表明，周歲生長發育性狀是中等偏高遺傳力的性狀。綜上所述，不同的研究得出不同結果的可能原因是使用的品種不同，不同的飼養環境條件以及不同的擬合模型，在大多數的動物模型中忽略了母體遺傳效應及其與直接加性遺傳效應的協方差，也有可能是該地區安格斯牛群體剛進入選擇階段，選擇強度較低，導致遺傳基礎一致性較差，即增大，遺傳力相應的增高。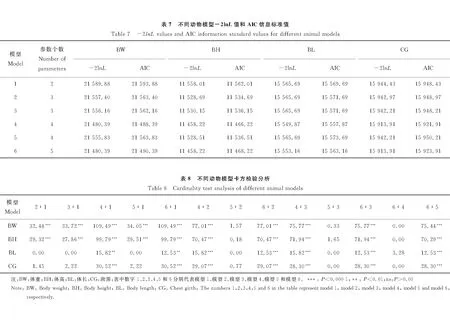

3.3 不同動物模型對周歲生長性狀遺傳參數估計的影響

本研究中，在考慮母體效應而不考慮母體遺傳效應與加性遺傳效應的協方差時(模型2、3和5)，與只考慮直接加性遺傳效應時(模型1)降低了直接遺傳力的估計值。因為在不考慮母體效應的情況下，母體方差的一部分將包括在加性遺傳方差的估計中。因此，包含母體效應將具有降低直接遺傳力估計值的效果。當同時考慮母體遺傳效應及其與直接加性遺傳效應的協方差時(模型4和6)，直接遺傳力和母體遺傳力值增加，總遺傳力值降低明顯。這可能與直接加性遺傳效應與母體遺傳效應間呈較強的負相關有關，表明母體遺傳效應對安格斯牛生長性狀的影響是負效應，即生長較快的母牛不一定有好的母性能力。因此在生長性狀遺傳參數估計時，需要考慮母體遺傳效應。體重、體高、體長和胸圍的總遺傳力估計值范圍分別為0.16±0.05～0.59±0.02、0.12±0.03～0.52±0.03、0.11±0.01～0.20±0.04和0.32±0.01～0.52±0.03，總遺傳力代表了基于表型值估計選擇反應的均值，估計可能受到所使用的品種、模型和數據大小的影響，在只考慮直接加性遺傳效應而不考慮其他效應影響的模型中，總遺傳力的估計值最高，母體效應及其與個體加性遺傳效應的協方差都具有降低總遺傳力估計值的影響。本研究不同動物模型中，母體永久環境效應估計值很低，甚至為零，表明該效應對總遺傳力估計結果影響較小，Gemeda等將母體永久環境方差歸因于母體的子宮狀況，與母體的子宮容量、母性的行為和妊娠晚期的飼喂有關，母性行為很可能反映了母體的生育能力。本研究通過研究不同動物模型的方差組分和遺傳參數間的差異性，篩選安格斯牛周歲生長性狀遺傳參數估計的最佳動物模型，以期為安格斯牛群體的育種方案優化，選育提高以及科學選種提供科學依據。

4 結 論

通過比較不同動物模型，確定模型4為寧夏地區安格斯牛周歲生長性狀遺傳參數估計的最佳模型，該模型考慮了母體遺傳效應及其與直接加性遺傳效應之間負的協方差對周歲生長性狀的影響在安格斯牛選擇中都需考慮。模型中母體永久環境效應估計值很低，該部分效應對性狀的表型影響較小，且可能隨著世代的增加而消失，故該部分效應對周歲生長性狀的影響可忽略。