汽車傳動軸振動的仿真分析與優化

王成明，張得富，陳云升

（1.鄭州大學機械與動力工程學院，河南 鄭州 450001；2.許昌遠東傳動軸股份有限公司，河南 許昌 461111）

1 引言

隨著我國汽車保有量的逐年增加，道路條件的改善以及人們環保意識的不斷加強，汽車的舒適度越來越受到大眾的關注。汽車傳動軸作為汽車動力傳遞的重要零部件，在高速旋轉的狀態下，所造成的過大的振動、異響等都直接影響汽車傳動軸部件本身以及其他關聯零部件的壽命[1-2]，同時嚴重影響乘客以及行人的身心健康。

某汽車傳動軸生產商采集的裝配該型號傳動軸乘用車的反饋中指出，在（90～100）km/h的行駛速度下，乘客明顯感受到振動加劇，經分析判斷主要原因是汽車傳動軸工作頻率與固有頻率接近，導致了共振。該型號乘用車因其軸距大，故采用2根傳動軸連接的方式，其中間支撐結構復雜、動態性能難以確定，這些因素制約著共振問題的解決。

長期以來，該公司采用傳統的測試方法，該方法只能針對已加工裝配完成的樣品，不能用于研發設計階段，而采用CAE方法進行模態分析具有方便更改設計方案、周期短、成本低等優點，因此，傳統生產模式亟需改變[3-4]。

這里應用Ansys有限元軟件對該型號乘用車傳動軸總成進行模態分析，并通過仿真分析方法的改進，建立更加準確的汽車傳動軸總成模型；應用Adams 建立虛擬樣機模型進行動力學仿真，得出精確的影響規律，為傳動軸總成的設計、中間支撐性能的確定、該型號乘用車減振降噪提供依據。

2 汽車傳動軸總成自由模態分析

2.1 傳動軸有限元模態分析

該乘用車傳動軸主要由滑動叉、前后軸管，中間支撐總成、十字軸萬向節總成、突元叉等零部件組成，如圖1所示。

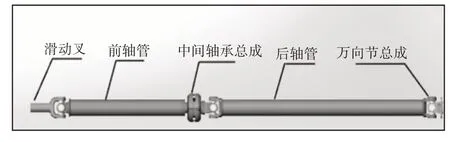
圖1 傳動軸總成結構圖Fig.1 Transmission Shaft Assembly Structure

所建傳動軸總成仿真模型盡量還原傳動軸實際結構特征以及各個零部件之間的連接方式，如軸承和軸頭，萬向節總成等裝配關系利用剛性單元模擬，并放開相應轉動自由度，保證有限元分析結果的準確性[5]。

前后軸管采用45#鋼，軸頭、萬向節總成、突元叉等采用40Cr，中間支撐采用天然橡膠，按實際情況定義各部分零部件材料，確保準確的物理特征及質量分布[6]。前后傳動軸管，軸頭部分等采用六面體實體單元，其余零部件采用四面體網格劃分，最終建立的節點單元為280816，模型單元數為126330。

由于傳動軸低階模態對該系統振動影響較大，高階模態影響較小，求解出其前4階自由模態，頻率及振型，如圖2、表1所示。

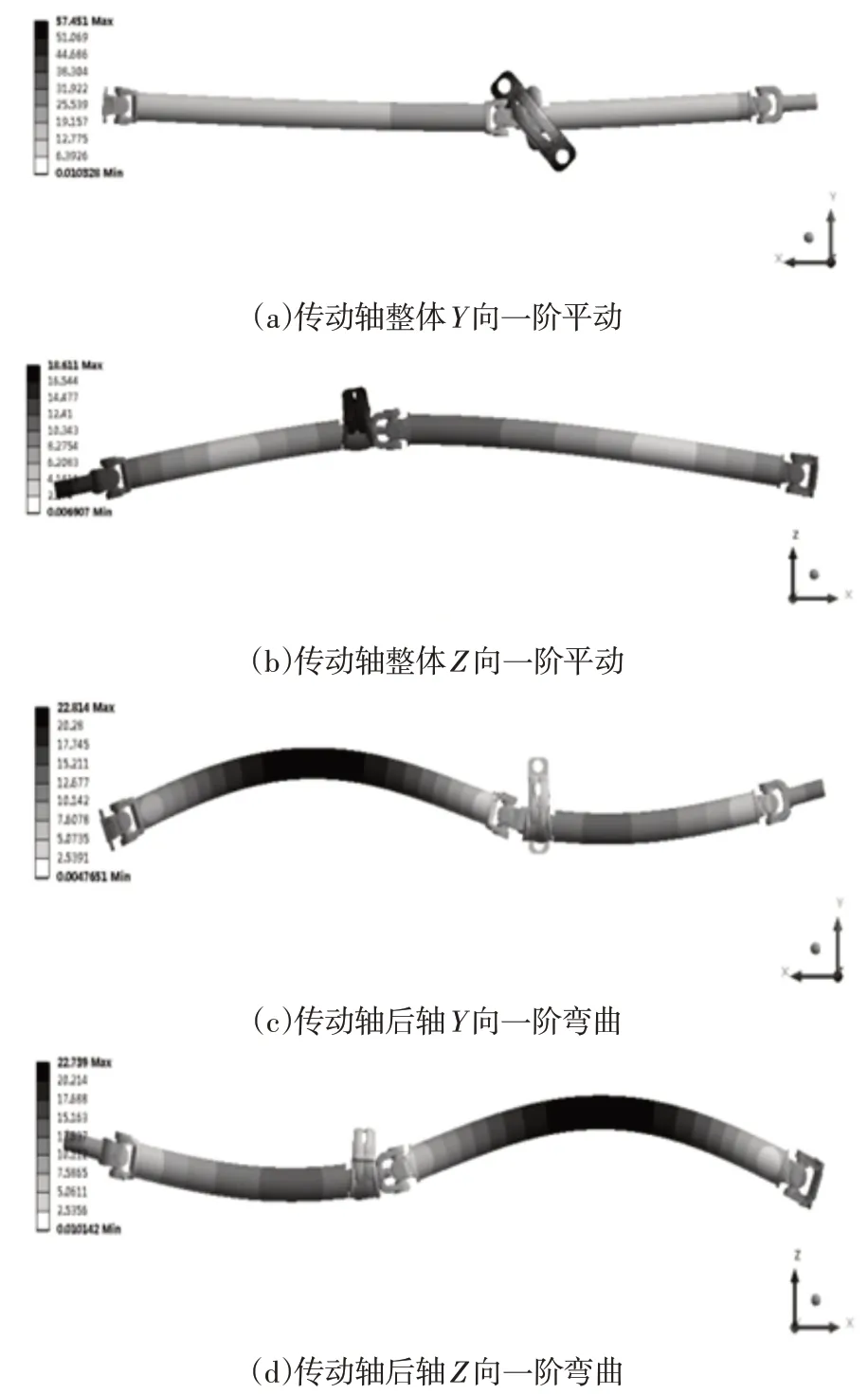
圖2 自由模態仿真振型圖Fig.2 Vibration Mode Graphics of Free Modal Simulation

表1 仿真分析結果Tab.1 Simulation Analysis Results

2.2 自由模態實驗分析

實驗測試采用比利時LMS 公司的Test.lab 模態分析系統、SIEMENS 40通道數據采集前端以及PCB模態傳感器等。測試方法采用錘擊實驗法，兩端以及中間支撐處采用尼龍繩懸掛，將該型號傳動軸14等分即15個等分點，三個三方向加速度傳感器分別貼裝在敲擊點2，7，13處布置，如圖3所示。以軸向為X向，采用力錘對（1～15）均勻分布點的+Y，+Z向分別敲擊5次，采集記錄模態數據。求解出其前4階模態，頻率及振型，如圖4所示。

圖3 實驗布置圖Fig.3 Experimental Layout

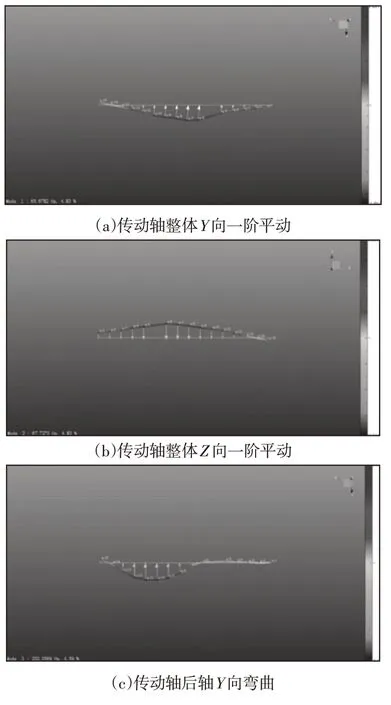
圖4 自由模態實驗振型圖Fig.4 Vibration Mode Graphics of Free Modal Experiment

2.3 結果分析

將仿真分析結果與實驗測試結果對比，如表2所示。可見各階次振型以及頻率基本一致，數值相近，平均相對誤差為3.58%，說明建立的仿真模型基本滿足要求，具有一定的實用價值。

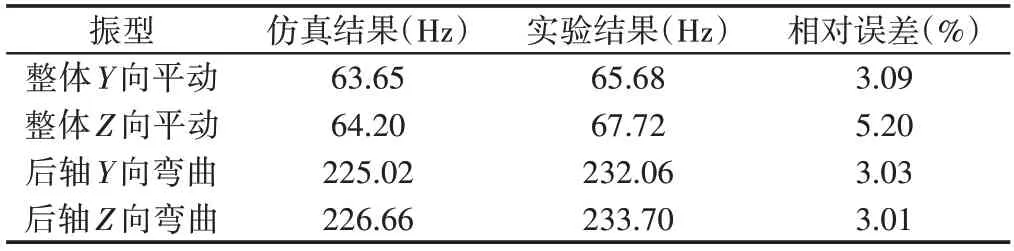
表2 仿真與實驗結果對比Tab.2 Comparison Between Simulation and Experimental Results

3 模型修正及分析

3.1 中間支撐總成性能試驗分析

由于中間支撐橡膠外形結構的復雜性，以及彈性模量的時變特性，使形狀不規則的中間支撐結構很難通過解析公式預測其剛度[7]，往往通過經驗取值進行仿真計算，導致該傳動軸總成的固有頻率、振型產生較大誤差，對分析結果造成一定影響，延長傳動軸設計優化的周期。傳動軸的振動通過中間支撐傳遞給底盤，影響汽車的舒適性，而軸向竄動影響較小，所以決定利用垂向和橫向彈簧連接替代中間支撐總成結構。隨機抽樣三個該型號中間支撐總成試件進行動靜態特性臺架實驗，以確定該型號中間支撐總成的實際剛度，實驗臺架及安裝方式，如圖5所示。

圖5 中間支撐動態性能實驗Fig.5 Dynamic Performance Experiment of Intermediate Support

根據中華人民共和國鐵道行業標準TB/T2843-2007《機車車輛用橡膠彈性元件通用技術條件》[8]中的靜態性能試驗方法，實驗采用正反兩方向加載卸載方式，對試件從零加載到實驗載荷上限，以加載速度卸載到零，反向加載到載荷下限，以相同速度卸載到零；第三次開始記錄載荷—變形曲線，如圖6所示。

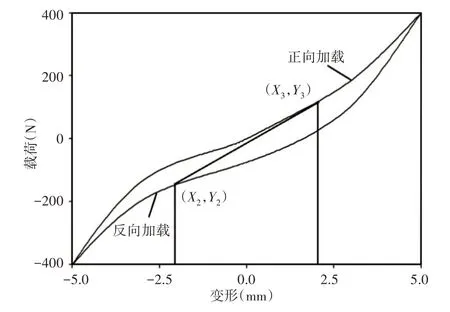
圖6 正反方向加載卸載、載荷-變形曲線Fig.6 Load-Deformation Curve Under Loading and Unloading in Both Directions

剛度K計算公式：

式中：Y1、Y2—載荷，單位（N）；X1、X2—變形，單位（mm）。

實驗結果，如表3所示。

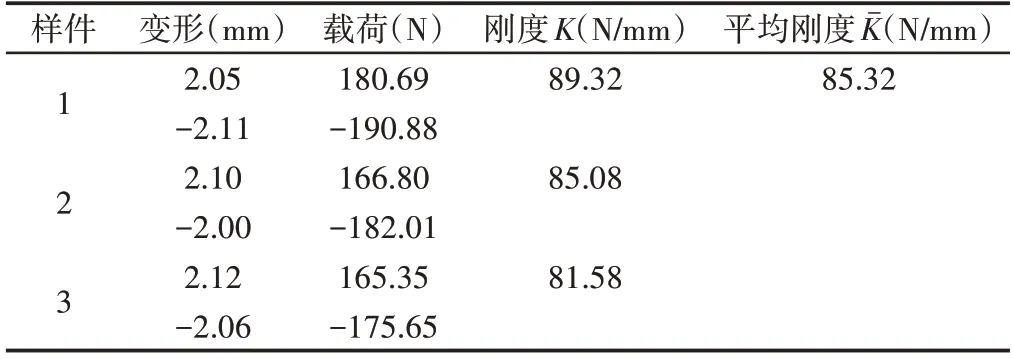
表3 剛度實驗結果Tab.3 Results of Stiffness Experiment

3.2 修正模型模態分析

根據傳動軸的實際安裝形式，以此約束傳動軸輸入端滑動叉和輸出端突元叉的六個自由度，彈簧單元一端固定軸承位置，一端固定于地面，如圖7所示。設置彈簧剛度為85N/mm，其它約束條件和裝配關系與自由模態分析一致。通過修正模型并進行約束模態分析求解，結果及振型，如表4所示。

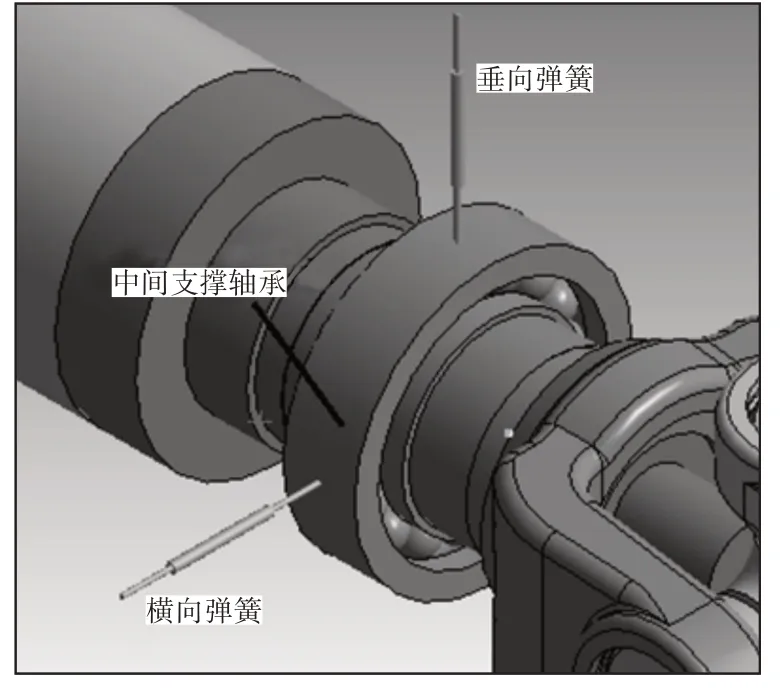
圖7 彈簧連接模型Fig.7 Spring Connection Model

表4 約束模態仿真結果Tab.4 Constrained Modal Simulation Results

3.3 結果分析

采用相同剛度的彈簧替換原來傳動軸總成中間支撐部件，并添加符合實際工況下的邊界約束，得到準確的仿真結果以及振型圖。由模態分析可知，傳動軸整體一階平動模態對應頻率大致為68Hz左右，傳動軸一階彎曲模態對應頻率大致為255Hz左右。根據振動理論可知，當激振頻率與固有頻率接近時會引起共振，發生異響，噪音增大，影響整車的安全性[9]。根據該車型的配置參數：發動機最高轉速5600r/min，最高檔減速比i1為0.778，車輪半徑0.316m，主減速比i為4.778。通過計算可知，一階平動模態頻率對應車速101.67km/h，與實際客戶反映的問題具有一致性，并且驗證了修正模型的正確性和分析結果的正確性。而一階彎曲模態對應的時速為381.28km/h，遠遠超出最高車速，不予考慮。傳動軸在設計階段，軸管長度、厚度、中間支撐的位置等都已經確定，不能通過優化設計該影響因素達到減振的目的，因此合理設計中間支撐的剛度是解決該問題的有效措施。

3.4 臨界轉速與安全系數

傳動軸臨界轉速nk計算方法與安全系數K通過以下公式計算[10]：

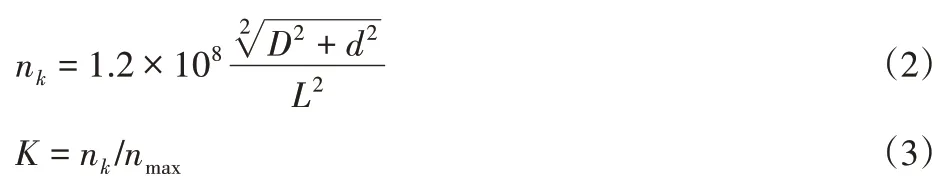
式中：D、d—軸管外、內徑（63.5mm、60.3mm）；L—兩萬向節中心距離（后軸為865mm）；nmax—傳動軸最大轉速；nmax=nemax/i1，nemax—發動機最高轉速；i1—最高檔減速比。根據上述參數計算得臨界轉速nk=14044r/min，K=1.95＞1.2，即滿足穩定性要求。

該傳動軸采用兩節傳動軸連接的方式，只理論校核較長的后軸存在一定的局限性，需要進行臺架實驗以驗證傳動軸總成的穩定性。安裝方式，如圖8所示。實驗參照QC/T523-1999《汽車傳動軸總成臺架試驗方法》[10]，隨機選取3件該型號傳動軸樣品，編號1#、2#、3#，激振發生器位于后軸中點，掃頻范圍取（0.5～1.2）nk對應的頻率范圍，即（117～280）Hz，掃頻步進為1Hz/s，如圖9、表5所示。

圖8 臨界轉速實驗布置圖Fig.8 Critical Speed Test Layout

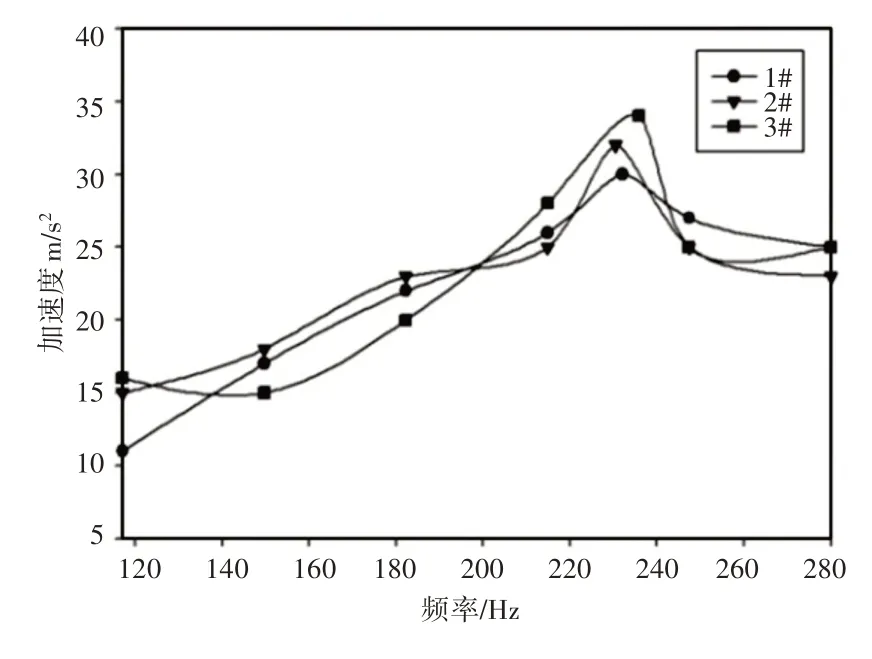
圖9 臨界轉速實驗掃頻圖Fig.9 Sweep Frequency Figures of Critical Speed Test

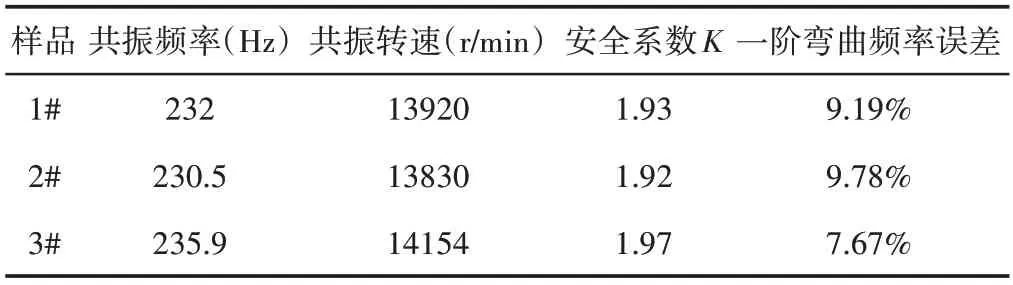
表5 臨界轉速實驗結果分析Tab.5 Analysis of Critical Speed Test Results

分析可知，隨機選取的傳動軸樣品共振頻率即為一階彎曲頻率，由于實驗臺架與激振設備的存在，與仿真分析約束條件存在一定的誤差，且最大不超過10%，驗證了仿真模型的正確性。同時計算安全系數均大于1.2，滿足穩定性要求，不會發生彎曲斷裂的情況。

4 中間支撐剛度優化設計

4.1 中間支撐剛度理論計算

根據系統隔振理論可知，隔振效果的好壞取決于振動傳遞率TA的大小。TA越小，表明通過隔振系統傳遞的力或者運動越小，隔振效果越好。TA的大小取決于系統的剛度K、阻尼系數C、阻尼比ξ的大小。無論阻尼比ξ取何值，當頻率比λ=ω/ωn>時，TA值小于1，隔振系統能起到真正的作用[7]。其中ω為激振頻率，是傳動軸轉動產生的，即軸轉動頻率；ωn為中間支撐固有頻率。由于在車速為（90～100）km/h產生劇烈振動，因此取范圍內平均車速v=95km/h=1583.3m/min計算，n=vi/2πr=3812.17r/min。

激勵頻率與中間支撐固有頻率之比：

中間支撐固有頻率：

中間支撐的剛度為：

式中：ω=2πn/60=399.06rad/s；m—中間支撐的支撐重量，傳動軸前軸5.5kg，后軸6.7kg，支撐重量m可認為是總重一半即m=6.1kg。

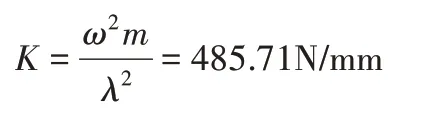
所以為了滿足系統隔振要求，在設計階段，中間支撐的徑向剛度應小于485.71N/mm。

4.2 中間支撐剛度參數優化設計

應用Adams仿真軟件對傳動軸建立虛擬模型，依據實際裝配條件對各個零件進行約束，萬向節總成建立胡克副，前后軸管與萬向節部分建立固定副，中間支撐以彈簧連接模擬，軸承與軸建立轉動副，滑動叉與突元叉與地面建立轉動副，在滑動叉（輸出軸）建立驅動，突元叉（輸出軸）輸入恒定的反扭矩模擬阻力矩，同時根據實際的安裝工況，調整后軸安裝角度為4°，從而建立實際的傳動軸動力學仿真模型，如圖10所示。

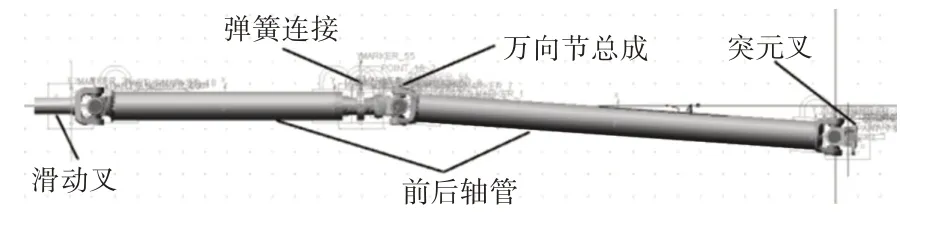
圖10 運動學仿真模型Fig.10 Dynamics Simulation Model

以中間支撐彈簧剛度為設計變量，剛度約束（0～1000）N/mm；以中間支撐軸承質心垂直方向加速度絕對值最大值為目標函數；約束函數是保證傳動軸真實的工況下運轉，即所添加的約束、負載、驅動、彈簧等條件。設置轉速分別為1000r/min、2000r/min、3000r/min、4000r/min探究不同轉速下剛度對加速度的影響規律，全面反映剛度參數優化的合理性結果，如圖11所示。

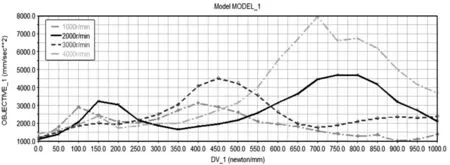
圖11 不同轉速下剛度參數優化設計Fig.11 Optimization Design of Stiffness Parameters at Different Speeds

由圖11 分析可知，在（0～75）N/mm 和（225～325）N/mm 范圍內，各個轉速下的目標值均較小。但剛度值過小會造成彈性元件難以支撐傳動軸總成的重量，引起穩定性等問題。因此，綜合中間支撐剛度值理論優化結果，剛度值應選擇（225～325）N/mm 較為合適，尤其剛度在275N/mm 附近時，對于不同轉速，其加速度均較小。

4.3 優化后結果分析

采用剛度優化到275N/mm，對車速95km/h即傳動軸轉速為3812.17r/min工況下，剛度優化前后中間支撐軸承加速度和振幅效果圖，如圖12所示。

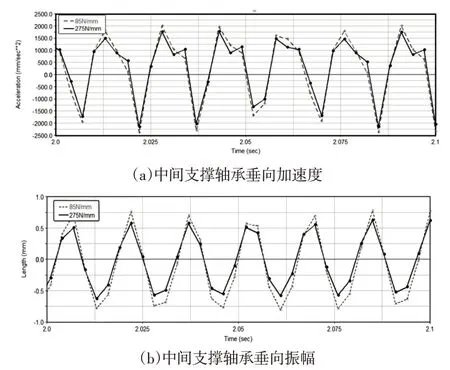
圖12 優化前后加速度和振幅效果圖Fig.12 The Effects of Acceleration and Amplitude Before and After Optimization

由圖12可知，剛度在85N/mm和275N/mm時加速度絕對值最大值分別為2293.28 mm/s2、2159.72mm/s2，降幅為5.82%；剛度在85N/mm和275N/mm時下振幅最大值分別為0.82mm、0.63mm，降幅為23.17%，因此該中間支撐剛度的優化方案有效，起到明顯的減振效果。

5 結論

（1）通過Workbench 對某型號汽車傳動軸總成自由模態分析與LMS Test.Lab實驗模態分析系統對該傳動軸總成自由模態臺架實驗分析對比，初步驗證了建立的仿真模型的正確性。分析結果表明傳動軸一階平動模態對應頻率為68Hz，對應轉速為4080r/min，車速為101.67km/h，位于傳動軸工作范圍內，是造成傳動軸劇烈振動的原因。

（2）通過中間支撐總成靜態特性實驗測定該型號中間支撐總成剛度為85N/mm，采用彈簧單元連接替代中間支撐總成的方法解決了中間支撐總成復雜的結構對仿真分析的影響，同時為中間支撐剛度參數優化提供指導。

（3）通過理論計算和實驗分析傳動軸臨界轉速，其安全系數均大于1.2，滿足穩定性要求。

（4）綜合中間支撐剛度理論優化和仿真參數優化結果，剛度值選取（225～325）N/mm 范圍內最為合適。且在275N/mm 時，加速度降幅5.82%，振幅減小23.17%。