平板結構法向振速的貝葉斯聲學反演方法

劉振宇，張二亮

（鄭州大學機械與動力工程學院，河南 鄭州 450001）

1 引言

由于結構的輕量化設計，現代機械裝備中平板類結構應用廣泛，但它們在服役過程中容易受激振動并產生噪聲。通過將平板類結構表面振速可視化，便于揭示結構的振動噪聲的產生與輻射機理，這對平板類機械零件的優化設計和振動控制具有重要指導意義。

傳統接觸式表面測量振動的方法快捷精確，例如采用加速度計測量，但此類方法容易導致因加速度計自身的質量而使其附著的平板動力學固有性質被改變的問題。非接觸式的測量方法能夠避免這類問題，例如利用光學儀器進行測量，諸如數字圖像相關法[1]或激光多普勒法[2]。近年來，利用麥克風陣列聲學測量來重構表面振速的方法引起國內外學者的廣泛關注，作為一類實用的非接觸式測量方法，逐漸發展起來。

利用聲學測量來回溯聲源的方法目前有如下幾類：基于空間傅里葉變換的近場聲全息法通過測量聲源面近場的聲壓，利用二維空間傅里葉變換將聲壓信息轉換到波數域，然后通過傳遞算子傳遞相關信息到重建面，最后再經過逆傅里葉變換獲得重建面上的振速[3]。基于邊界元的方法通過建立聲源面和全息面以及預測面之間的振聲傳遞矩陣，利用奇異值分解對該矩陣求逆，并結合測得的聲壓數據來重建聲源表面的振速，該方法適用于不規則的聲源面，但計算效率和精度均受許多限制[4]。等效源法通過有限數量虛擬等效源的聲場疊加來替代振動體的輻射聲場，通過匹配振動體表面的法向振速得到虛擬源的強度[5-6]。基于貝葉斯的聲源重建方法能充分融合先驗信息，基于邊際似然最大化實現正則化參數的尋優，實現了先驗信息和似然函數（數據信息）的最佳匹配，能夠較高精度地重構聲源表面振速[7-8]。

經過技術不斷地探索與發展，文獻[9]開發了實時近場聲全息技術，利用在時間-波數域中格林函數的采樣來連續地計算聲壓場。文獻[10]改進了實時近場聲全息技術，實現平板表面法向振速的重構。文獻[11]利用聲壓與質點法向速度之間的聯系改進了時空域近場聲全息技術，實現平板表面瞬時法向振速的重構。文獻[12]在貝葉斯方法的基礎上利用循環維納濾波器對循環平穩聲源的表面振速進行重構。文獻[13]對于稀疏聲源的表面重構問題提出了一種迭代貝葉斯聚焦法。文獻[14]針對聲源重構技術中麥克風陣列位置的布局給出了一種優化方法。

基于近場聲壓測試數據，應用貝葉斯方法研究平板類結構表面振速的測量問題，首先概述了利用麥克風陣列進行聲學測量的方法，然后給出了貝葉斯方法重構聲源的具體過程和關鍵步驟，最后通過簡支平板的振動噪聲仿真和自由平板的噪聲測試實驗驗證提出方法的有效性。

2 表面法向振速重構的貝葉斯方法

2.1 麥克風陣列聲學測量

通過麥克風陣列對平板進行聲學測量的方法，如圖1所示。假設聲源是聲源面S上的感興趣區域，p(ri)是M個麥克風傳感器在不同的位置ri，i=1，...，M處測量的聲壓數據。針對特定頻率ω，麥克風陣列測得的聲壓數據p(ri)與待重構的聲源（法向振速）v(r)之間的機理模型為：

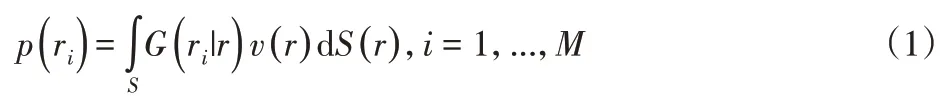
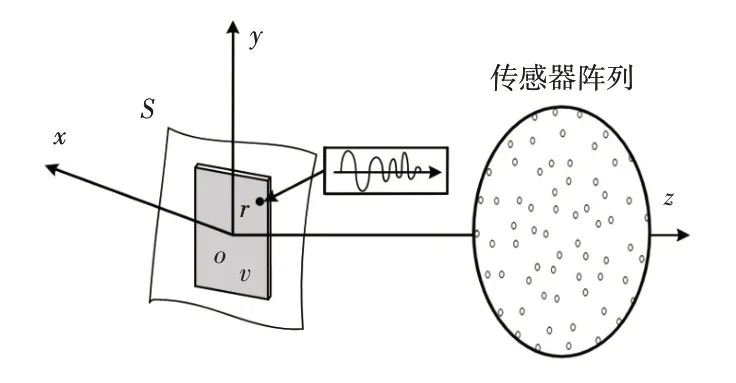
圖1 麥克風陣列聲學測量Fig.1 Acoustic Measurement by Microphone Array

式中：G(ri|r)—聲源面S上的不同位置r與麥克風的位置ri之間的振速-聲壓轉換和格林函數；n(ri)—測量噪聲。在文中，為保持符號的簡潔，頻率變量ω不再標出。聲源重建即通過聲壓數據p(ri)的測量，回溯聲源面法向振速v(r)的分布。一般情況下，聲源可表示為：

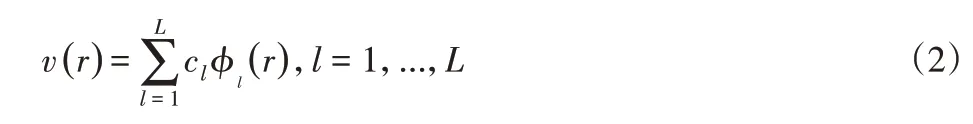
式中：cl—由傳感器測量的聲壓數據所決定的系數；?l—獨立于測量數據的空間基函數，用于聲源空間分布的插值。估計振速v(r) 的問題歸結為尋找插值基函數?和聲壓數據中所包含的系數c的問題。

用p∈CM×1表示所有位置ri處的聲壓數據，系數c∈Cl×1和測量噪聲n∈CM×1的第i個元素分別為ci和n(ri)。式（1）的矩陣形式為：

其中，G的元素可表示為：

利用傳感器測得的聲壓數據重構出聲源v(r)，r∈S涉及到傳播算子G的偽逆，重構結果往往是不適定的，存在不唯一性和不穩定性，需要正則化策略以獲得滿意的反演結果。

2.2 貝葉斯方法

本工作應用貝葉斯聲源反演方法[7]，研究平板結構的法向振速重構。如上所述，用Φ和c來表示插值基函數和系數，法向振速分布表示為v(c，Φ) 。貝葉斯方法的思想是將聲壓數據下的振速分布視為通過c和Φ參數化的隨機場[v(c，Φ)|p（]其中［］表示隨機變量的概率密度函數）。通過后驗概率分布[v(c，Φ)|p]的最大化，獲得最優參數

基于貝葉斯公式，后驗概率密度函數可以表示為：

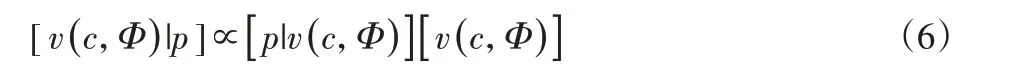
式中：∝—正比例；[p|v(c，Φ)]—似然函數，表示在給定一個振速分布v(c，Φ)下觀察到測量聲壓數據p的概率；[v(c，Φ)]—先驗概率分布，表征關于振速分布的所有先驗信息（物理信息，專家知識等）。

根據中心極限定理，測量噪聲n在頻域內服從循環復高斯分布，即[n]=CN(0，λ2IM)，其中λ2代表噪聲的平均功率，IM是M×M單位陣。那么測量聲壓的概率密度函數（似然函數）為：

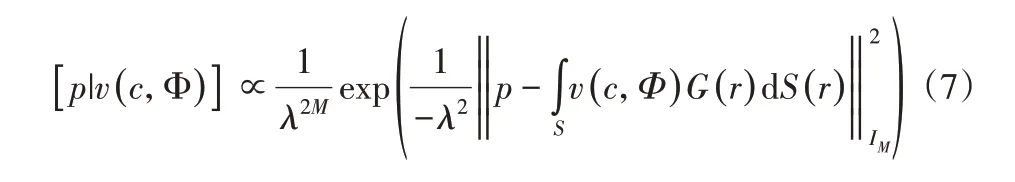
假設先驗概率密度函數[v(c，Φ)]也服從循環復高斯分布，即[v(c，Φ)]=CN(0，γ2IM)，其中，γ2—聲源的平均功率；Iv—單位矩陣。此時法向振速的空間協方差函數定義為：

孔徑函數的作用是通過獲取振速（聲源）的先驗空間位置信息，限定平板結構振速重構的區域，其原理，如圖2所示。結合空間位置先驗信息，振速的先驗概率分布可以表示為：

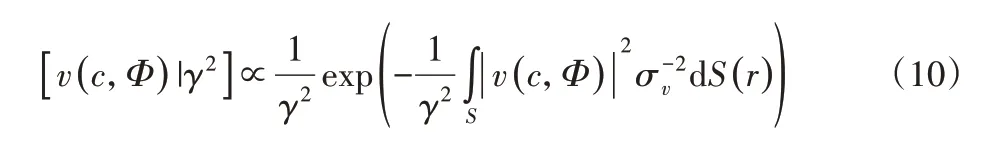
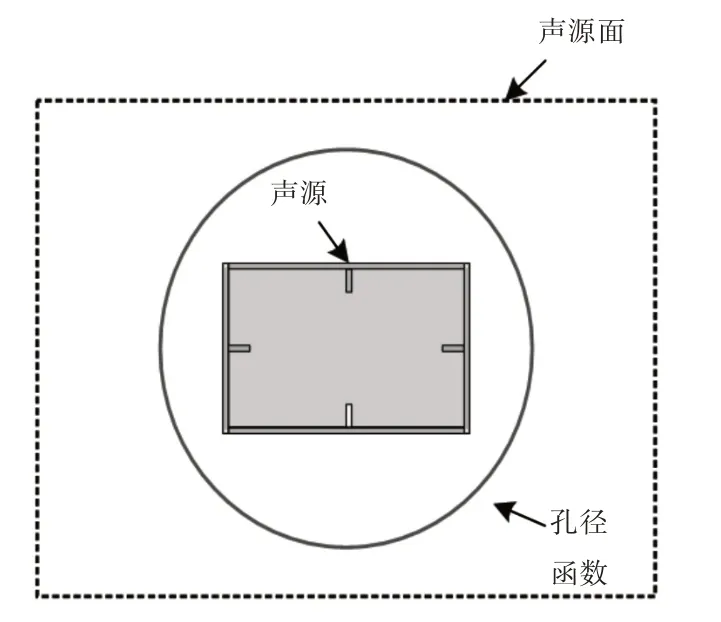
圖2 孔徑函數 的概念解釋Fig.2 The Explanation of Aperture Function

將似然函數和先驗概率分布代入貝葉斯式（6），得到后驗概率密度函數，對其取負對數，得：

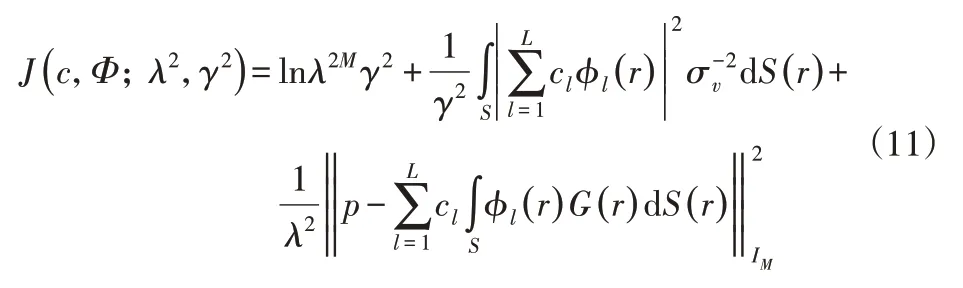
將平板表面均勻劃分N個單元，那么相應得到格林函數G∈CM×N。對格林函數進行奇異值分解，G=USVH，得到參數和L：

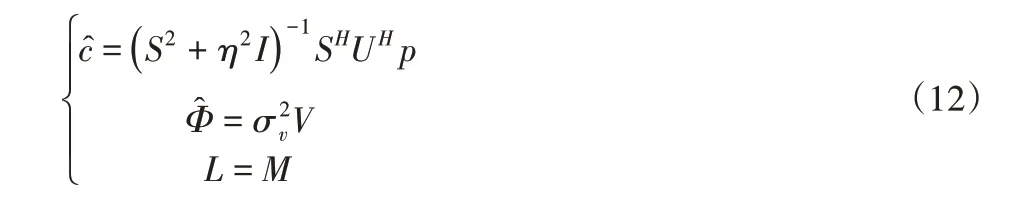
最后，振速的反演結果為：

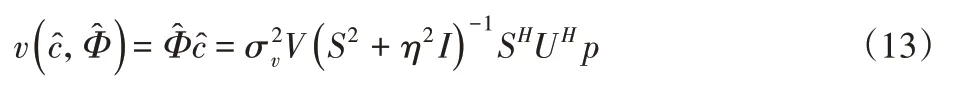
式中：η2—正則化因子，η2=λ2/γ2。η2的最優值可以通過邊際似然最大化來獲得。也就是：

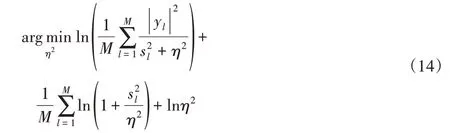
式中：yl=UH p；sl—S對角陣上的元素。

3 仿真算例

3.1 仿真方案

仿真用的矩形簡支平板（1×1）m，厚度h=0.002m，彈性模量E=2×1011Pa，密度ρ=7800kg/m2，泊松比μ=0.3，平板的瑞利阻尼系數α和β分別為10-2和10-4。聲源傳播介質為空氣，聲速c=340m/s。使用的麥克風陣列為直徑1m的圓形支架，傳感器位置的隨機分布參，如圖1所示。

平板與傳感器所在平面之間距離z=0.2m。采用隨機激勵，且作用于平板中心。通過ANSYS軟件計算簡支平板的固有頻率與模態振型數據，然后利用模態疊加法得到平板表面的時域速度和加速度響應。將平板表面的時域速度數據進行快速傅里葉變換得到頻域內平板的理論表面振速。

設置仿真中采樣頻率為2048Hz，采樣時間為40s。基于傳感器與平板在聲場中的空間位置信息以及平板表面的加速度響應，利用時域瑞利積分生成聲場內所有傳感器位置處的仿真聲壓信號。這些聲壓數據用于法向振速的貝葉斯重構。本例選擇孔徑函數為邊長1m的矩形，以（1～1000）Hz為關心頻帶，重構平板的表面振速。

3.2 仿真結果

以平板中心位置為參考點，分析重構的表面振速與理論值之間的差異，其對比結果，如圖3所示。

圖3表明，貝葉斯重構的表面振速和理論表面振速在整個頻帶內幅值接近，相對誤差較小。平板的理論表面振速在86Hz處的分布，如圖4所示。該頻率下重構的表面振速，如圖5所示。可以看出二者吻合很好。

圖3 平板表面振速的理論值與重構值Fig.3 Theoretical Value and Reconstructed Value

圖4 平板的理論表面振速分布Fig.4 Theoretical Surface Velocity Distribution

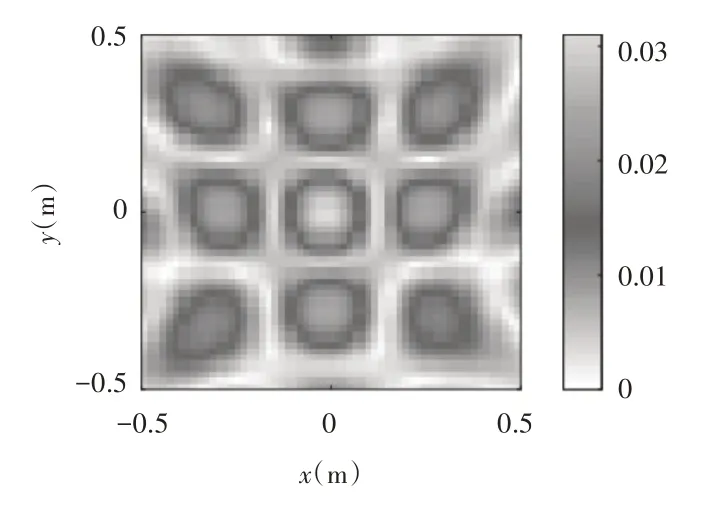
圖5 平板的重構表面振速分布Fig.5 Reconstructed Surface Velocity Distribution

4 噪聲測試實驗

4.1 實驗方案

為進一步驗證貝葉斯方法重構平板表面振速的精度，開展了自由平板振動噪聲實驗。矩形平板尺寸為（0.4×0.4）m，厚度為0.003m，利用橡皮筋懸掛模擬自由邊界條件，如圖6所示。實驗中所用的陣列支架與仿真算例相同。

圖6 激振平板信號采集實驗Fig.6 Signal Acquisition Experiment

激振器與平板的中心連接，進行單點隨機激振。平板與傳感器所在的平面平行且距離z=1m，采樣頻率為8192Hz，采樣時間為300s。在貝葉斯算法中，選擇孔徑函數為邊長0.25m 的矩形。實驗室的環境峰值噪聲約為50dB。

在矩形平板的不同位置安裝加速度傳感器，這些傳感器記錄的加速度數據，經過數值積分得到速度數據，用于驗證算法的重構精度。

4.2 重構結果

將實驗采集的聲壓數據應用于貝葉斯方法，得到（0～700）Hz頻帶內平板的表面振速。其中430Hz處的重構的平板表面振速分布相對于陣列支架的位置，如圖7所示。與實際空間位置吻合。

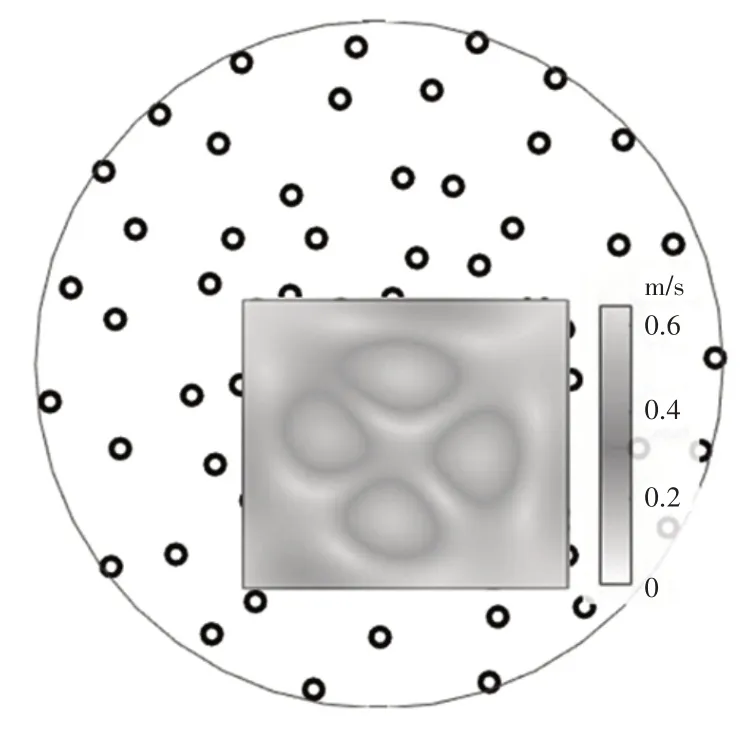
圖7 重構表面振速分布（430Hz）Fig.7 Reconstructed Surface Velocity Distribution

以平板的中心為坐標原點，選取平板上位置為（0.05m，-0.1m）的加速度傳感器的數據為參考，積分得到振速數據，再通過快速傅里葉變換得到表面振速的測量值。將之與相同位置處的重構表面振速進行對比，如圖8所示。可見，平板的振動噪聲測試實驗驗證了本文采用貝葉斯振速重構算法的有效性。

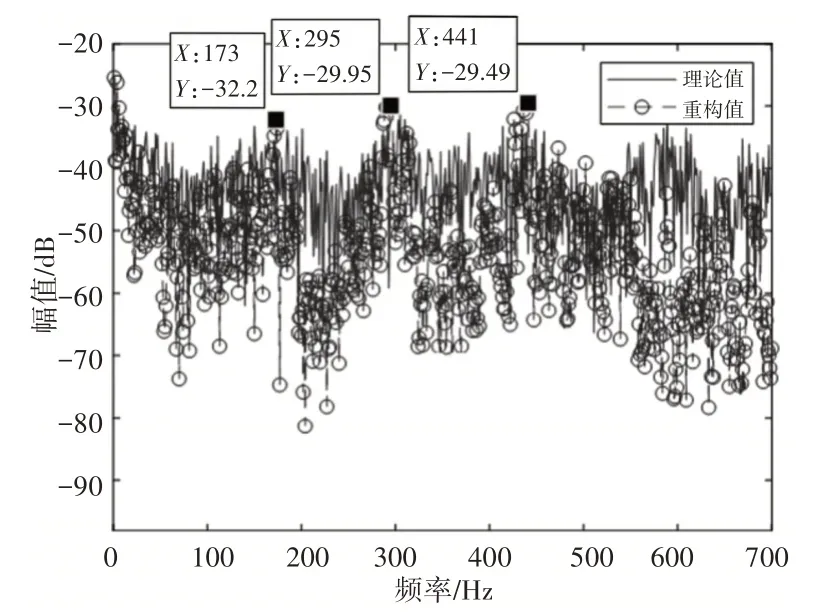
圖8 平板的重構表面振速與實測表面振速Fig.8 Reconstructed Surface Velocity and Measured Surface Velocity of Plate

5 結論

利用了平板類結構近場輻射的聲壓數據，開展了基于貝葉斯方法的表面振速重構應用研究。仿真和噪聲實驗結果都表明，近場貝葉斯聲全息方法是重構平板類結構表面法向振速的有效方法。這將為平板類結構的非接觸式振動測試提供新手段，對于開展輕質結構的振動噪聲控制和優化設計具有重要意義。