基于Hoek-Brown強度準則的淺埋隧道掌子面穩定性分析

張世民付開黃睿楊樺郭帥

（1.紹興文理學院土木工程學院，紹興 312000；2.浙大城市學院土木工程系，杭州 310015；3.浙江省巖石力學與地質災害重點實驗室，紹興 312000；4.浙江省建設工程質量檢驗站有限公司，杭州 310012；5.浙江華蘊基礎工程有限公司，湖州 313200）

0 引言

淺埋盾構隧道中，施加合理的支護力能夠保證掌子面的穩定性，當掌子面前方施加的支護力不足或者過大時將引起掌子面發生破壞，支護力不足時將導致淺埋盾構隧道的主動破壞，支護力過大時將導致被動破壞。為此，淺埋隧道掌子面的穩定性已受到廣泛的關注［1］。目前研究淺埋隧道掌子面穩定性的常用方法主要為室內模型試驗、理論推導、數值模擬等。Leca等［2］構建了淺埋隧道掌子面的主動和被動破壞兩種模式，基于極限分析理論研究了淺埋隧道掌子面的穩定性。Soubra［3］在Leca等［2］提出的破壞模式的基礎上進行了改進，得到了淺埋隧道掌子面的三維破壞模式，獲得掌子面穩定性的最優的上限解。李得建等［1］構建了傾斜地表條件下淺埋隧道掌子面的三維被動破壞模式，引入非線性強度準則研究了掌子面的穩定性。陽軍生等［4］提出了自適應性有限元網格技術，構建淺埋隧道掌子面的破壞模式，進行了各種參數下有限元的計算，揭示了掌子面穩定性的精細化的破壞模式。

當巖土材料處于飽和狀態時，巖土工程的穩定性受材料之間的孔隙水壓力的影響顯著［5］。Skempton［6］首次將孔隙水壓力引入到極限分析中，基于有限元技術研究邊坡的穩定性，研究表明孔隙水壓力對邊坡的穩定性影響顯著。Huang等［7］基于極限分析理論，利用巖土材料的非線性Mohr-Coulomb強度準則，并考慮孔隙水壓力的作用分析其對隧道塌落的影響。Yu等［8］在極限分析定理的框架內研究了考慮孔隙水壓力作用下的深埋隧道拱頂塌落，結果發現孔隙水壓力對隧道拱頂塌落有著顯著的不利影響。

本文基于極限分析定理，考慮孔隙水壓力的作用，構建出二維有限多塊體的淺埋隧道掌子面的被動破壞模式，為研究其穩定性本文引入了經典的Hoek-Brown破壞準則。結合極限分析定理和虛功率原理得到了淺埋隧道掌子面被動破壞模式下的極限支護力的表達式，利用非線性規劃函數解出其上限解。通過參數分析，研究了工作面穩定性的影響因素。

1 淺埋隧道被動破壞機制

1.1 基本假設條件

在淺埋隧道掌子面穩定性的分析中合理應用極限分析理論的前提是假設隧道周圍巖土體應視作為服從相關聯動法則的理想的剛性塑性體，可忽略其變形［9-11］。因此，本文方法的解析解是基于上述基本假設，主要針對軟弱圍巖提出，以完善目前對淺埋隧道掌子面的穩定性評價。

1.2 被動破壞模式構建

構建淺埋隧道掌子面的被動破壞模式見圖1，該破壞模式由有限個平動的剛性多塊體組成，P表示為隧道掌子面上作用的極限支護力，本文構建的淺埋盾構隧道掌子面的二維剛性有限多塊體破壞機制見圖1，h為隧道的開挖高度，H為淺埋隧道的埋深。

圖1 淺埋隧道掌子面的被動破壞模式Fig.1 The passive failure mode of shallow tunnel face

1.3 破壞準則

本文采用Hoek-Brown破壞準則，該準則經過多年的不斷發展，該準則已經經過多次的修正，最新的表達形式為［12-13］

式中：σ1和σ3分別為巖土材料破壞時的最小和最大主應力；a、s和mb通過試驗可獲得［14-15］，具體計算見式（2）—式（4）。

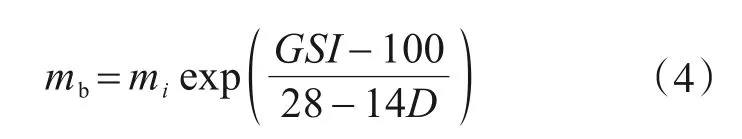
式中：D表示擾動因子；mi為試驗中可獲得的無量綱常數；GSI表示為地質強度指標。

經過等效Mohr-Coulomb強度準則中的內摩擦角和黏聚力可以用Hoek-Brown破壞準則的參數來表示：

式中，σ3n表示室內三軸試驗中的最大圍壓。

1.4 計算過程

淺埋隧道掌子面的被動破壞模式中的幾何和速度關系見圖2，在機動許可速度場中三角剛性體OC1C2的速度假定為v1，速度v1的數值不為0。根據破壞機制中各塊體之間的幾何關系和速度關系［14］如下。

圖2 幾何、速度關系Fig.2 The geometric relationship and velocity relationship

1.4.1 速度關系

根據各個三角塊體的速度組成的三角關系得到如下速度的關系：

破壞模式中，剛性三角塊體的速度的方向和垂直方向的夾角為βi：

1.4.2 幾何關系

圖1所示的剛性塊體的邊長可根據三角形的正弦和余弦定理得到，表達式分別如下：

圖1破壞機制中各個剛性塊體的面積表達式分別為

1.4.3 功率計算

利用極限分析定理，圖1所示的淺埋隧道掌子面的被動破壞機制中的重力所做的功率可表達為

淺埋隧道掌子面的被動破壞機制中各速度間斷線上產生的耗散能為

淺埋隧道掌子面上需要施加支護力，支護力在機動許可速度場中所做的功為

孔隙水壓力為土壤或巖石中地下水的壓力，可作為一種外力引入到極限分析定理中，在圖1的破壞機制中，孔隙水壓力在不同邊界上做的功如下：

（1）首先在邊界CiCi+1上所做的功可以表示為

（2）在破壞機制的上部邊界OA上所做的功可以表示為

（3）同樣地，在邊界CBn+1上孔隙水壓力所做的功可以表示為

根據上述討論，孔隙水壓力在機動許可速度場中做的總功是各邊界上做的功之和，可以表示為

在虛功原理中，機動許可速度場中破壞機制內的內部耗散能總是和外力所做的功是相等的，即

聯合式（19）—式（26），可以推導得到淺埋隧道掌子面被動破壞模式下的極限支護力的表達式為

1.5 極限支護力優化求解

在極限分析定理的框架內，通過理論推導得到了淺埋隧道掌子面破壞機制下極限支護力的目標函數的表達式，利用多目標規劃函數進行求解，求解之前需要確定目標函數的約束條件。

然后給出本文方法的計算流程圖，如圖3所示。

圖3 計算流程圖Fig.3 Flow chart of calculation

2 合理性驗證

利用MATLAB軟件進行多目標優化時，本文提出的機制中三角塊體的數目取1～30，孔隙水壓力系數取ru=0，隧道開挖高度h=10 m，重度γ=18 kN/m3，地質強度指標GSI=11.53，巖體單軸抗壓強度σci=2.92 MPa，mi=25，擾動因子D=0。從圖4可知，H/h=1，當塊體數目不斷增大到3時極限支護力達到了1 213 kPa，并且此后極限支護力基本保持不變，說明本文機制中塊體數目為3時得到的極限支護力的數值精度已經滿足需要［15］。

圖4 極限支護力隨三角塊體數目變化圖Fig.4 Change of ultimate support force with the number of triangular blocks

然后給定計算出不同的H/h下淺埋隧道掌子面的被動破壞機制下的極限支護力，參數如前所述，然后取不同的H/h（1、1.5、2及2.5）進行數值計算，將本文的解同參考文獻［1］中的方法和數值模擬的解進行對比，如圖5、圖6所示，三種方法得到的極限支護力的解與H/h的變化趨勢是一致的，即隨著H/h的增大而增大，且最大誤差為4.03%，說明本文求解淺埋隧道掌子面的被動機制下的極限支護力的方法是合理的。當然埋深對淺埋隧道掌子面的穩定性的影響還需要結合大量現場工程情況和試驗進行深入的研究。

圖5 結果比較Fig.5 Comparison of the results

圖6 本文方法和數值模擬得到的破壞范圍對比Fig.6 Comparison of failure range obtained by this method and numerical simulation

3 參數影響分析

3.1 孔隙水壓力系數

淺埋隧道埋深H和開挖高度h均取8 m，孔隙水壓力系數ru=0～0.9，重度γ=18 kN/m-3，地質強度指標GSI=10，巖體單軸抗壓強度σci=2.92 MPa，mi=25，擾動因子D=0，計算的塊體數目取30。通過求解得到如圖7（a）所示的不同孔隙水壓力系數下的淺埋隧道掌子面的極限支護力，由圖7（a）可知，隨著孔隙水壓力系數的增大，淺埋隧道掌子面的被動破壞機制下的極限支護力也不斷增大。圖8（a）表示的是不同孔隙水壓力系數下淺埋隧道被動破壞的范圍，孔隙水壓力系數的增大將導致掌子面的被動破壞范圍也增大，說明淺埋隧道被動破壞機制下掌子面的穩定性受孔隙水壓力的影響明顯。

3.2 地質強度指標

孔隙水壓力系數ru取0～0.8，地質強度指標GSI取10、20及30，剩余參數同3.1節。根據圖7（b）所示的計算結果，孔隙水壓力系數取不同的數值時，淺埋隧道掌子面的被動破壞機制下的極限支護力隨地質強度指標GSI的變化趨勢相同，均隨著地質強度指標GSI的增大而降低，這是由于被動破壞機制內的內部耗散能隨地質強度指標GSI降低從而需要降低極限支護力，以減小外部力所做的功，虛功率原理得到滿足［15］；不同地質強度指標GSI的淺埋隧道掌子面的被動破壞范圍如圖8（b）所示，當地質強度指標GSI不斷增大時，淺埋隧道掌子面的被動破壞范圍不斷減小。

圖7 掌子面的極限支護力參數影響分析Fig.7 Analysis of the influence of the parameters of the ultimate support force of the face

3.3 參數

孔隙水壓力系數ru=0～0.8，無量綱參數mi=5～25，地質強度指標GSI=20，擾動因子D=0，其他參數同3.1節中內容。計算得到的極限支護力隨著參數mi的變化趨勢見圖7（c），被動破壞機制的內部耗散能隨著參數mi的增大而降低，從而導致極限支護力減小［15］；不同參數mi的淺埋隧道掌子面的被動破壞范圍見圖8（c），當參數mi增大時，淺埋掌子面的被動破壞范圍不斷減小。

3.4 擾動因子

孔隙水壓力系數ru=0～0.8，地質強度指標GSI=15，擾動因子D=0～0.2，其他參數同3.1節中內容。在不同孔隙水下的極限支護力隨著擾動因子D的變化趨勢見圖7（d）。當擾動因子D的增大時極限支護力也不斷地增大；不同擾動因子D的淺埋隧道掌子面的被動破壞范圍見圖8（d），當擾動因子D增大時，淺埋隧道掌子面的被動破壞范圍減小。

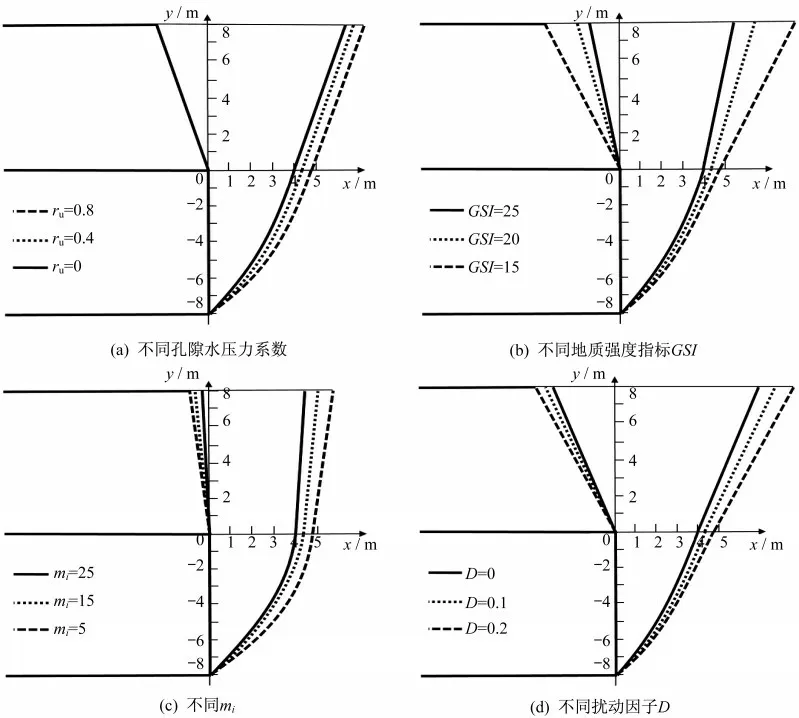
圖8 掌子面的破壞范圍參數影響分析Fig.8 Analysis of the influence of failure range parameters of the face

4 結論

（1）本文構建了淺埋隧道掌子面的二維平動有限多塊體的被動破壞機制，基于極限分析定理并考慮孔隙水壓力的作用，利用Hoek-Brown強度準則得到了淺埋隧道掌子面的被動破壞機制下的極限支護力的表達式，通過多目標規劃求解可得到極限支護力的上限解。

（2）本文方法得到的淺埋隧道掌子面的被動破壞機制下的極限支護力的上限解和既有文獻的解隨著H/h的變化趨勢一致，最大誤差為4.03%，并且破壞范圍基本一致，證明本文方法是合理的。

（3）通過對淺埋隧道掌子面的被動破壞機制下的極限支護力和破壞范圍的參數影響進行分析，研究表明：隨著孔隙水壓力系數ru和擾動因子D的增大，淺埋隧道掌子面的被動破壞機制下的極限支護力和破壞范圍均呈現出不斷增大的趨勢，而隨著地質強度指標GSI和參數mi的增大呈現出不斷減小的趨勢；孔隙水壓力對淺埋隧道掌子面的被動破壞機制下的極限支護力和破壞范圍影響顯著。

本文方法適用于處于軟弱圍巖的淺埋盾構隧道掌子面的穩定性分析，對于深埋隧道和傳統礦山法施工隧道適用性還需要進一步研究。