鋼管混凝土桁架系桿拱橋穩定性分析

金成棣葛耀君，2徐勝乙，*

（1.同濟大學土木工程防災國家重點實驗室，上海 200092；2.同濟大學橋梁結構抗風技術交通運輸行業重點實驗室，上海 200092）

0 引言

鋼管混凝土桁架拱肋是啞鈴形鋼管混凝土拱肋斷面形狀的一種變體。鋼管間距離拉大以提高拱肋的抗彎剛度，其間不再由連續鋼板聯系組合，而是以鋼管組成三角形桁架形式作為聯接件，組成拱肋的組合截面。在此，由于三角桁架腹桿的變形，表征著鋼管間的組合效果。在計算拱肋面內穩定性時，首先要確定組合效應系數，研究組合件節段長度變化，對聯接件斜桿斜度的布置優化，使組合效應系數達到最佳狀態，接著在此基礎上按縱向撓曲變形的組合模態計算拱肋面內臨界力。對于面外穩定性的計算，當采用二管組合截面的條件下，豎平面內的聯接件對它不起作用，如采用四管兩兩組合，上、下兩管平面內聯接件就存在變形影響。由于兩管組合的單榀拱肋抗面外失穩的能力較低，一般需設縱向聯接系。因此，在此需要對縱向聯接系作組合效應分析。

對于面外穩定性分析，考慮吊桿力偏移時的非保向力效應，提高拱肋的穩定性是非常重要的方面，這種基于二階變形理論為基礎的穩定性分析是裸拱系桿拱橋設計的理論基礎。在此將做出驗算公式推導，并以具體算例說明相關運算。

1 鋼管混凝土桁架拱肋的系桿拱橋面內穩定性分析

1.1 用三角形桁架組合的雙鋼管混凝土拱

根據組合柱理論，拱肋的組合慣性矩Iz等于：

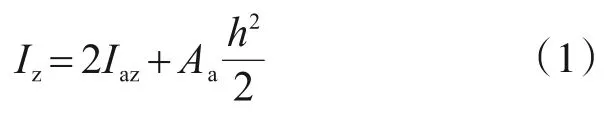
式中：Iaz為單根拱肋的換算慣性矩；Aa為拱肋的換算面積；h為鋼管混凝土的上、下兩管的中心距離。

在此：

式中：Es，Ec為鋼材及混凝土彈性模量；Ac，As為混凝土及鋼管面積；d，t分別為鋼管外徑及壁厚。

兩端鉸接的中心受壓組合柱，用三角形桁架組合的臨界壓力推廣應用于二鉸拱［1］，即按曲桿拉直計算臨界軸壓力Hkp等于：

式中：Ea為拱肋計算彈性模量，根據式（2），Ea=Ec；Es，AD分別為斜桿材料彈性模量及面積；lD為斜桿的長度；a，cosφ(x)為斜桿水平投影長度及拱軸線在點x處的切角余弦；μla中μ為屈曲系數，二鉸拱μ=0.54［2］，la為拱軸線長度，它近似等于：

式（4）根據斜桿變形所產生的剪切變形，它反映三角形桁架對上、下鋼管的組合效果，在此把αi定義為節段i的組合效應系數，它等于：

根據式（6），在設計上采取優化布置，一般h及吊桿間距由總體布置所決定，同時從構造上考慮，吊桿錨箱設置在斜桿與鋼管軸線的交點位置為宜，斜桿與鋼管軸線的交角以45°為最佳。因此，簡單說來，在此尺寸a接近于h是優化布置目標。

假設拱肋設計軸力為Nd，拱的水平推力Hd沿跨徑不變，近似地，由拱軸力Nd對拱軸線縱向撓曲ω(x)的彎矩M(x)=Hdω(x)cosφ(x)。縱向撓曲的曲率變化與彎矩的關系用材料力學公式表示如下，在此近似取ds=dxcosφ(x)，則

式中：ω(x)與拱肋失穩時變形模態有關，二鉸拱計算長 度（屈曲）l0=μla=0.54la及Nd=Hdcosφm，

注意兩點，縱向撓度曲線的零點位置在x=0.54l附近，最低臨界荷載發生在處。為了運算方便，將撓度曲線設定為對稱與反對稱組合。

假設

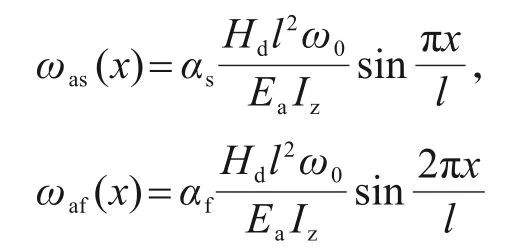
式中，αs及αf分別為跨中及四分點的最大撓度系數。

近似地取x=0.54l為撓度曲線零點位置，并取

將縱向撓曲的撓度曲線表達成：

為了確定αs及αf，將式（7）分別以及求解，在此，采用差分法求解微分方程式，得到差分表達式如下：

由式（9）、式（9'）和Nd=Hdcosφ(x)的方程組得到

代入式（8'），得到表達式（10）

將式（10）系數表達成：

則得到：

根據變形相容條件，當Hd達到Hkp時，

式（12）為用三角形桁架組合的鋼管混凝土拱肋面內臨界水平力。

1.2 拱梁共同作用的面內穩定性分析

考慮了鋼管混凝土桁架拱肋條件，由拱肋單位變形ω0=1吊桿所產生的附加分布力，用Hd表示，等于［3］：

式中：y(x)為吊桿長度，近似地等于拱軸線縱坐標；a為吊桿間距。

由式（13）及式（13'）計算跨徑為l的彎矩，由沿長度直線分布，它對拱及梁引起的彎矩MFˉ，f(x)及MFˉ，s(x)是相同的。

由彎矩MFˉ，f(x)及MFˉ，s(x)引起拱的撓度由差分法計算得到：

式中：m為分段數

式（14）應 分 別 按MFˉ，f(x)及MFˉ，s(x)計 算 得到然后得到λ以及ωa，Fˉ，c，它等于

同時，彎矩MFˉ，f及MFˉ，s引起梁的撓度由差分法計算得到：

式中：m為分段數

式（16）應 分 別 按MFˉ，f(x)及MFˉ，s(x)得 到然 后 得 到λ以 及ωb，Fˉ，c，它等于

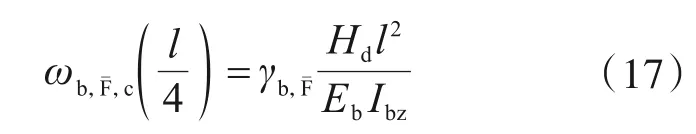
最后，得到鋼管混凝土桁架拱肋考慮拱肋共同作用的臨界水平力，它等于：

當梁拱剛度EbIbEaIaz≤5時，可以按簡化公式考慮拱梁拱剛度疊加計算共同作用的臨界水平力［4］，它等于：

1.3 鋼管混凝土桁架拱面內穩定性驗算

圖1中表示了跨徑lp=120 m的鋼管混凝土桁架系桿拱虛擬的總體布置及相關各部分尺寸。矢跨比f/l=1/5，拱軸線為拋物線，相關幾何參數見表1。

圖1 跨徑lp=120 m的鋼管混凝土桁架系桿拱橋總體布置（單位：cm）Fig.1 Overall arrangement of concrete-filled steel tubular truss tied arch bridge with a span of 120 m（Unit：mm）

表1 跨徑lp=120 m矢跨比=的下承式系桿拱橋相關幾何參數 Table 1 Geometrical parameters of a through tied arch bridge with a span of 120 m and a span ratio of 1/5

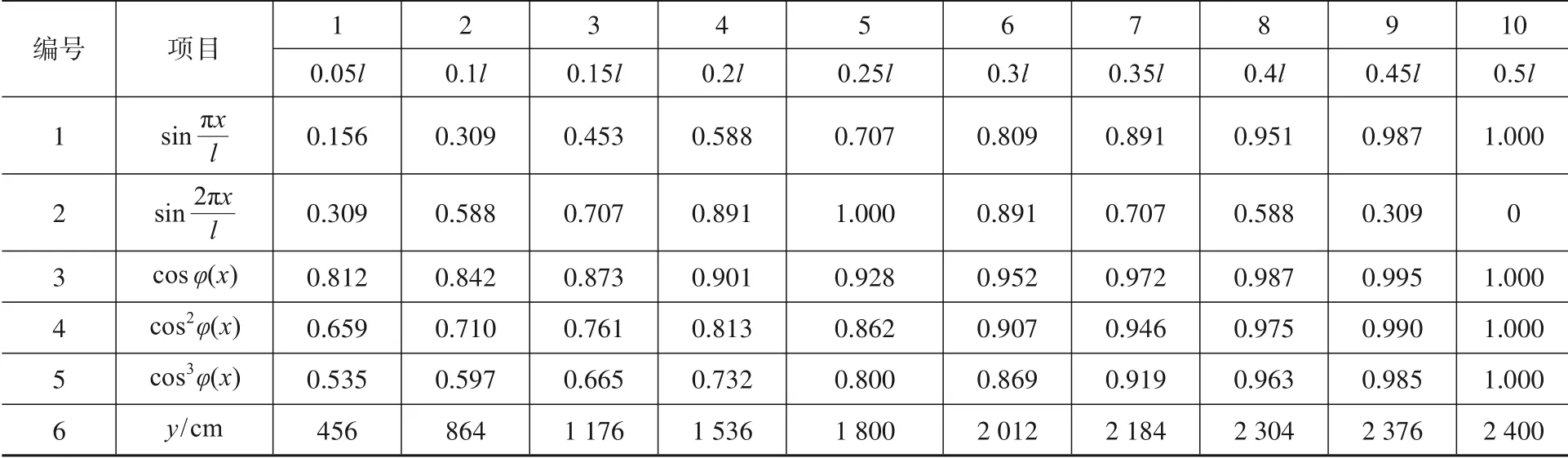
表1 跨徑lp=120 m矢跨比=的下承式系桿拱橋相關幾何參數 Table 1 Geometrical parameters of a through tied arch bridge with a span of 120 m and a span ratio of 1/5

編號1 2 3 4 5 6項目sin πx l sin 2πx l cos φ(x)cos2φ(x)cos3φ(x)y/cm 1 0.05l 0.156 0.309 0.812 0.659 0.535 456 2 0.1l 0.309 0.588 0.842 0.710 0.597 864 3 0.15l 0.453 0.707 0.873 0.761 0.665 1 176 4 0.2l 0.588 0.891 0.901 0.813 0.732 1 536 5 0.25l 0.707 1.000 0.928 0.862 0.800 1 800 6 0.3l 0.809 0.891 0.952 0.907 0.869 2 012 7 0.35l 0.891 0.707 0.972 0.946 0.919 2 184 8 0.4l 0.951 0.588 0.987 0.975 0.963 2 304 9 0.45l 0.987 0.309 0.995 0.990 0.985 2 376 10 0.5l 1.000 0 1.000 1.000 1.000 2 400

鋼管混凝土拱肋尺寸：

單 管：φ800×20，Es=2.1×104kN/cm2，As=490 cm2，Is=3.73×105cm4。

雙管組合：

中距：h=220 cm，b×h=80 cm×300 cm，Ias=2.373×105+490×22022=1.26×107cm4。

混凝土：

換算截面：

（兩管上、下組合截面）。

鋼管有關尺寸見表2。

表2 鋼管間聯接件尺寸和節間內斜腹桿節點間距Table 2 Size of the connection between the steel pipes and spacing between nodes of diagonal web members cm

系梁尺寸：橋面寬30 m，梁高2 m，橋面板厚度h=25 m，系梁寬2×200 cm，中距同拱肋2 200 cm。

吊桿尺寸：As=42 cm2，Ey=2.05×104kN/cm2。

鋼管間聯接件：斜桿及橫撐，采用φ300×12，AD=Ap=108.6 cm2，Ip=1.13×104cm4。

縱向聯接系k式桁架：E=2.1×104kN/cm2；豎桿（橫撐）第一檔φ1 200×20，Ap1=741 cm2，Ip1=1.29×106cm4；其余各檔φ800×16，Ac=394 cm2，斜桿φ600×16，Ac=294 cm2。

縱向聯接系總體尺寸：h=2 200 cm，1 200 cm cosφ(x)。cosφ(x)為拱軸線在點xi的切角余弦。

設計拱水平推力Hd=2.5×104kN榀，吊桿力V=2 000 kN根，間距a=600 cm。各部分尺寸詳見圖1及圖2。

圖2 縱向聯接系詳圖（單位：cm）Fig.2 Longitudinal connection system（Unit：mm）

鋼 管φ800×20 mm充 填C50混 凝 土，兩φ300×12 mm鋼管按三角形組合，斜桿尺寸見表2，如圖2虛線所示。鋼管混凝土換算面積Aa=1.5×104cm2（雙管），Iaz=1.9×108cm4（雙管未乘組合效應系數）。

組合效應系數αi按下列公式計算：

二鉸拱lD=0.54la，f l=1 5，la=1.1067l［2］。

見表2。代入上式得到表3的αi計算值。

表3 組合效應系數αi計算值Table 3 Calculated value of combined effect coefficient αi

組合效應系數αi=0.87，接近于等截面，近似地按等截面組合桁架拱確定面內臨界水平力，它等于：

本例通過優化分析，得到αi接近于常量，但在一般情況下，αi是變量，為了說明拱肋面內穩定性計算的差分法求解，結合算例說明運算過程，算例Δx=6m，m=20，利用對稱及反對稱只算半跨。差分方程組代入消元的系數表示如下：

在此a10，10為消元最終點：

在此反對稱以a5，5為消元最終點：

按式（9）及式（9'）計算在拱軸力作用下縱向撓曲的撓度計算。

鋼管拱肋由拱軸力引起縱向撓度，有關幾何尺寸數據見表1；鋼管拱肋由拱軸力引起縱向撓曲撓度計算，對稱見表4，反對稱見表5。

表4 鋼管拱肋由拱軸力引起縱向撓曲撓度計算（m=20，對稱）Table 4 Deflection calculation of longitudinal deflection of steel tube arch rib caused by axial force of the arch（m=20，Symmetric）

表5 鋼管拱肋由拱軸力引起縱向撓曲撓度計算（m=20，反對稱）Table 5 Deflection calculation of longitudinal deflection of steel tube arch rib caused by axial force of the arch（m=20，Antisymmetric）

計算結果按公路橋規二鉸拱驗算臨界力與差分法計算臨界力兩者基本吻合。考慮共同作用，用簡化法計算。

考慮拱梁共同作用用差分法驗證。

根據式（13）及式（13'）計算由拱肋單位位移ω0=1，使得吊桿力產生附加分布力用Hd表示，并分解成對稱與反對稱，見表6。由吊桿附加力及引起的彎矩MFˉ，f(x)及MFˉ，s(x)見表7及表8。由于它們沿跨徑長度沿直線分布，對于拱及兩的彎矩是相同的。

表6 由ω0=1引起吊桿附加力及計算Table 6 Calculation of additional forceandcaused by ω0=1

表6 由ω0=1引起吊桿附加力及計算Table 6 Calculation of additional forceandcaused by ω0=1

項目Fˉqf(x)=5.69sin 2πx l y()x ·Hd×10-5 Fˉqs(x)=5.69sin πxl y()x ·Hd×10-5 1 3.86 1.95 2 3.87 2.03 3 3.88 2.18 4 3.52 2.19 5 3.11 2.24 6 2.69 2.29 7 2.11 2.32 8 1.45 2.35 9 1.09 2.36 10 0 2.37

表7 由引起彎矩計算（反對稱）MFˉ，f(x)Table 7 Calculation of bending moment（Antisymmetric）MFˉ，f(x)caused by

表7 由引起彎矩計算（反對稱）MFˉ，f(x)Table 7 Calculation of bending moment（Antisymmetric）MFˉ，f(x)caused by

編號1 2 3 4 5 6項目Fˉq，f(x)×3.6Hd(3)×μi，i+1(1)+(2)(3)÷a′i，i(6)×μi+1，i(4)+(5)1 13.9 0 13.9 6.9 40.5 47.4 2 13.9 6.9 20.8 13.9 81.0 94.9 3 14.0 13.9 27.9 20.9 100.6 121.5 4 12.7 20.9 33.6 26.9 107.1 134.0 5 11.2 42.5 53.7 134.8 0 134.8 6 9.7 9.8 19.5 15.6 107.1 122.7 7 7.6 5.4 13.0 9.8 92.1 101.9 8 5.2 2.0 7.2 4.8 68.0 72.8 9 3.9 0 3.9 2.0 36.4 38.4 10 0 0 0 0 0 0

表8 由引起彎矩計算（對稱）MFˉ，s(x)Table 8 Calculation of bending moment（Symmetric）MFˉ，f(x)caused by

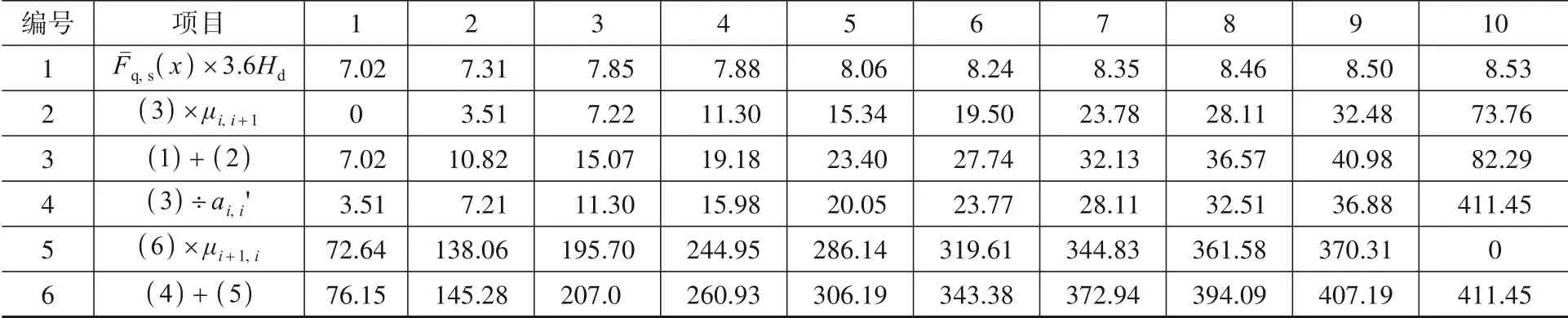
表8 由引起彎矩計算（對稱）MFˉ，s(x)Table 8 Calculation of bending moment（Symmetric）MFˉ，f(x)caused by

編號1 2 3 4 5 6項目Fˉq，s(x)×3.6Hd(3)×μi，i+1(1)+(2)(3)÷ai，i′(6)×μi+1，i(4)+(5)1 7.02 0 7.02 3.51 72.64 76.15 2 7.31 3.51 10.82 7.21 138.06 145.28 3 7.85 7.22 15.07 11.30 195.70 207.0 4 7.88 11.30 19.18 15.98 244.95 260.93 5 8.06 15.34 23.40 20.05 286.14 306.19 6 8.24 19.50 27.74 23.77 319.61 343.38 7 8.35 23.78 32.13 28.11 344.83 372.94 8 8.46 28.11 36.57 32.51 361.58 394.09 9 8.50 32.48 40.98 36.88 370.31 407.19 10 8.53 73.76 82.29 411.45 0 411.45

由算例已知吊桿Es=2.05×104kN/cm2，As=42 cm2，Hd=2.52×104kN，a=600 cm，

將及按直線分布的附加力計算彎矩列于表7中。

分別有f及s。

分別計算拱軸單位位移時引起吊桿分布力對拱反彈的對稱模態位移值和反對稱模態位移值，然后確定ωa，Fˉ，c及ωb，Fˉ，c，最終確定

由表7彎矩計算拱的撓度見表9。

表9 由彎矩MFˉ，f(x)計算拱的撓度（m2=400，反對稱）Table 9 Calculating the deflection of the arch )from the bending moment MFˉ，f(x)（m2=400，Antisymmetric）

表9 由彎矩MFˉ，f(x)計算拱的撓度（m2=400，反對稱）Table 9 Calculating the deflection of the arch )from the bending moment MFˉ，f(x)（m2=400，Antisymmetric）

編號1 2 3項目MFˉf()x l2Hd m2EaαiIz cos2φ()x(3)×μi，i+1(1)+(3)1 0.21 0 0.21 2 0.39 0.11 0.49 3 0.48 0.33 0.81 4 0.47 0.61 1.08 5 0.45 1.47 1.92 6 0.39 0.37 0.76 7 0.31 0.18 0.49 8 0.22 0.06 0.27 9 0.11 0 0.11 10 0 0 0

由表6彎矩計算拱的撓度見表10。

表10 由彎矩MFˉ，s(x)計算拱的撓度m2=400，對稱）Table 10 Calculating the deflection of the archfrom the bending moment MFˉ，s(x)（m2=400，Symmetric）

表10 由彎矩MFˉ，s(x)計算拱的撓度m2=400，對稱）Table 10 Calculating the deflection of the archfrom the bending moment MFˉ，s(x)（m2=400，Symmetric）

編號1 2 3 4 5 6項目MFˉs()x l2Hd m2EaαiIz cos2φ()x(3)×μi，i+1(1)+(2)(3)÷ai，i′(6)×μi+1，i(4)+(5)1 0.34 0 0.34——2 0.6 0.17 0.76——3 0.79 0.51 1.3——4 0.92 0.98 1.9——5 1.02 1.52 2.54 2.01 34.78 36.79 6 1.09 2.11 3.2 2.61 39.12 41.74 7 1.13 2.74 3.88 3.23 42.42 45.65 8 1.16 3.39 4.55 3.86 44.61 48.48 9 1.18 4.05 5.23 4.49 45.70 50.19 10 1.18 9.42 10.6— —53.0

由表8彎矩計算梁的撓度見表11、表12。

表11 由表7的彎矩MFˉ，f計算梁的撓度（m=20，反對稱）Table 11 Calculating the deflection of the beam from the moment MFˉ，f in 7（m=20，Antisymmetric）

表12 由表8的彎矩MFˉ，s計算梁的撓度（m=20，對稱）Table 12 Calculating the deflection of the beam from the moment MFˉ，s in table 8（m=20，Symmetric）

根據式（17）計算變形系數［4］，它等于（其中αac表5后按式（10）計算）

2 鋼管混凝土桁架拱肋面外穩定性分析

2.1 裸拱肋的穩定性分析

鋼管混凝土桁架拱肋的面外穩定性分析，對算例上、下兩管組合，只對面外內穩定性有影響，對面外沒有影響。只有采用三管或四管組合時，則拱肋上下兩個層面的鋼管采取的組合構件處理，需要如面內穩定性考量那樣，計算組合效應系數。方法可參考面內進行，但在此，橫向撓曲的模態常規為半波正弦曲線。為了鋼管間組合腹桿的多樣化，根據大多數在鋼管的上下層面采取框架式，在此忽略橫撐的直接剪切影響，組合效應系數αi等于：

式中：a為橫撐間距；cosφ(x)為拱軸線切角余弦；E，Ip，Ap為橫撐材料的彈性模量，橫撐屈曲平面內慣性矩及面積；la為拱軸線拉直長度。

一般情況，由于柱Iay較大，第一項可以忽略，則式（20）得到簡化。

確定了αi值后，可按變截面拱由差分法計算橫向撓曲的撓度線，它等于：

面外失穩時，變形模態一般取半波正弦曲線，因此得到：

可得到：

2.2 拱肋設置k式桁架縱向聯接系的穩定性分析

雙鋼管混凝土桁架拱肋的面外薄弱的穩定性，需要在兩榀拱肋間設置縱向聯接系，經比較框架式聯接系構造簡單，線條簡潔，一般設計人員樂于采用，但它的組合效果較差，特別在兩榀拱肋間距較大的情況下，在此，建議k式桁架，它的組合效果遠勝于框架式聯接系，根據廣義位移的推導，得到組合效應系數，表示如下：

式中：Iy為組合慣性矩，見式（1），在此h兩榀拱肋中心距；Ea為鋼管材料彈性模量；la為拱肋弧長，見式（3）說明；a為k式桁架沿拱跨度方向節段斜桿的投影長度；AD為斜桿面積；Ac為橫撐面積；E為聯接件材料彈性模量；cosφ(x)為節段對應于拱軸的切角余弦。

根據αi的變化，鋼管混凝土桁架組合拱在Hd軸力作用下的縱向撓曲的曲率變化與彎矩Hd·v(x)的關系式表示如下：

式中，Hd為組合拱的設計軸力，應該是兩倍的單榀拱肋的設計軸力。

2.3 雙鋼管混凝土拱肋面外穩定性驗算

換算截面

必須設置縱向聯接系，為了取得較好的組合效果，設置k式桁架。組合慣性矩等于：

根據式（25）計算k式桁架聯接組合效應系數αi，將結果列于表13中。

表13 k式桁架聯接系效應系數Table 13 k-type truss connection system effect coefficient

各節段效應系數相同，僅第一節段為滿足建筑凈空要求，它采取特殊形式，屬于框架聯接系，橫撐加大尺寸，采取φ1 200×20 mm，Ip1=1.29×106cm4，并設隅支撐200 mm×200 cm，由于拱肋腳段采取加大尺寸的鋼筋混凝土段b×h=250×310 cm，見圖2，Iay=1.56×107cm4。拱肋局部彎曲的變形影響可以忽略，而橫撐變形反彎點恰在斜桿支點，因此按式（16）的hi等于

根據拱肋面外失穩的變形模態，臨界軸力發生在跨中，第一節段剛度雖有所削弱，但對總體穩定性影響不大，近似地取：

計算

四鋼管桁架拱肋的面外穩定性

橫斷面布置如圖3所示，鋼管上下層的平面采用框 架 式，聯 接 件φ300×12，Ac=108.6 cm2，Ip=1.13×104cm4，a=400 cm（在三角形斜桿焦點位置，上、下鋼管錯位），h=1 600 cm，Ac=4 536.0 cm，As=

（兩根鋼管組合）

拱腳段截面見圖3，Iy=4.04×108cm4。

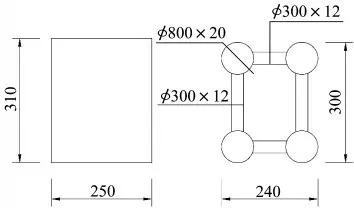
圖3 拱腳段截面（單位：cm）Fig.3 Cross section of the arch springing（Unit：cm）

根據式（21）計算組合效應系數：框架式略去第一項影響

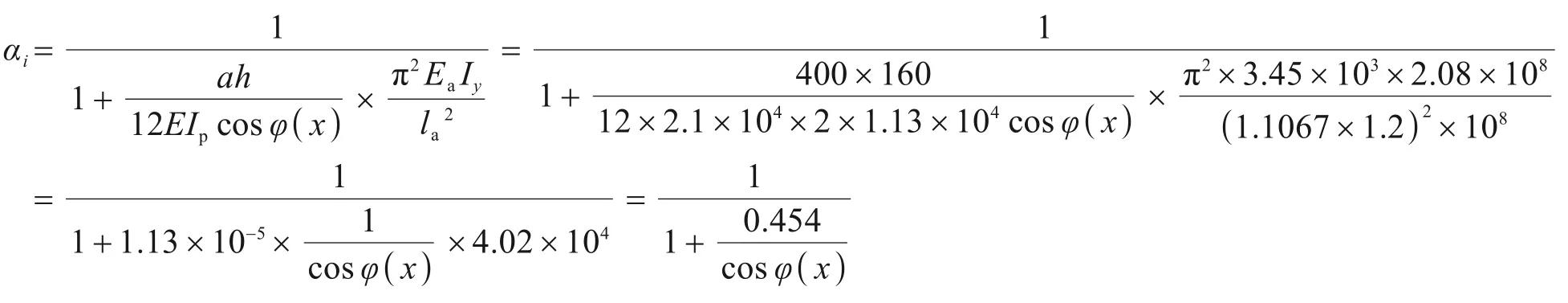
框架式聯接組合效應系數

計算點1的α1值：

經計算拱肋局部彎曲的變形很小，近似地取α1=α2。

根據式（22）計算四鋼管混凝土組合拱肋的面外臨界變形，見表14。

表14 四根鋼管桁架拱肋撓度計算（m2=400）Table 14 Calculation of deflection of four steel pipe truss arch ribs（m2=400）

3 考慮吊桿力偏移對拱肋面外失穩時扶正力影響

系桿拱側向穩定性分析，吊桿力偏移時水平分力為拱肋失穩時扶正力［4］，它等于：

對于跨中：

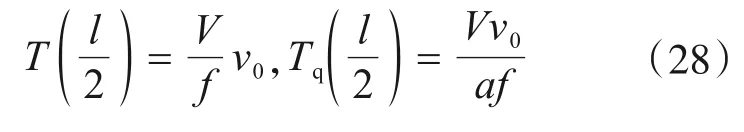
式中，a為吊桿間距。

根據計算統計，由扶正力引起彎矩近似地等于

由扶正力引起彎矩Mt(x)與撓度曲線曲率變化的關系式：

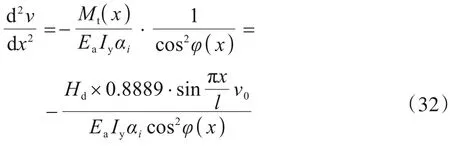
將式（25）用差分公式表示如下：

其中Ea=3.45×103kN/cm2，Iy=2.08×108cm4。

αi見式（20），計算結果等于0.641～0.688，sin及cos2φ(x)見表1，吊桿附加力引起撓度，計算見表15。

表15 吊桿附加力的扶正作用，拱的撓度計算Table 15 Arch deflection calculation considering the uprighting effect of the additional force of the suspender

根據表14的計算結果：

考慮吊桿扶正力后：

其中，Hkp(1)為未考慮吊桿力偏移扶正力影響的臨界軸壓力；Hkp(2)為考慮吊桿扶正力后的結果，其比值為7，說明了考慮吊桿扶正力后能夠大幅度提高計算得到的拱肋臨界軸壓力。

4 結語

本文利用連續在上海公路雜志上所發表的關于系桿拱橋穩定性的文章相關內容，系統地研究了鋼管混凝土桁架系桿拱橋的穩定性，就面內穩定性而言，當兩鋼管間設置三角形桁架聯接件，并對斜桿的角度控制在30°～60°，接近45°時，可以取得很好的組合效應，α沿跨徑基本上接近常數，等于0.87，考慮拱梁共同作用，臨界荷載系數達到18.3，按《公路鋼筋混凝土及預應力混凝土橋梁設計規范》（JTG D62—2004）相關規定，均能得到滿意的結果，對面外穩定性，像啞鈴形鋼管拱肋一樣，必須設置縱向聯接系以保證面外穩定性，當縱向聯接系采取k式桁架式，并對斜桿布置的傾斜度優化，可以得到最佳效果。

論文研究了四鋼管組合桁架拱肋的獨榀拱肋布置。在此，面內穩定性就像常規系桿拱一樣，穩定性條件特別好，對于面外穩定性，鋼管桁架拱比啞鈴形稍差些，通過計算，必須考慮吊桿力偏移時扶正力的影響。抗壓承載力從理論上符合設計要求，但在實踐上最好通過實驗手段取得確證。對于中小跨徑，實驗證明，這樣橫斷面布置，只要認真對待，詳細復核計算，完全是可靠的。裸拱系桿拱橋由于施工及制造上的不正確，初始變形條件下，對穩定性影響很大，而大跨徑系桿拱橋的施工難度比中小跨徑困難得多。

在論文中，為了結合公路橋規鋼筋混凝土正截面抗壓承載力驗算及鋼結構容許應力法驗算，都需要確定l0/r，從而得到φ值。對不同的計算模型，采取了兩種模式：對于設置縱向聯接系的條件，l0=la，而對于非保向力影響，μ=