一種基于四方定理與幻方的矩形圖像置亂方法*

李向軍,喻 鵬,劉伯成,袁凌利

(1.南昌大學軟件學院,江西 南昌 330046；2.南昌大學數學與計算機學院,江西 南昌 330031)

1 引言

當前互聯網和多媒體系統的快速興起導致了文字、圖像和視頻等內容快速激增，與此同時，海量數據的安全性卻受到極大挑戰。保護用戶隱私、提升數據安全性越來越受到各方重視。

圖像具有數據量大、信息冗余度高以及相鄰像素間相關性強等固有特點。傳統文本加密方式，例如數據加密標準DES、高級加密標準AES 、RSA和橢圓曲線加密ECC等[1 - 4]在保障數字圖像安全傳輸與存儲方面缺乏足夠的速度和能力，直接將現有加密體制用于圖像加密是不合適的。因此，大量基于不同技術的圖像加密算法被研究人員提出，以緩解上述問題。

圖像置亂是實現圖像加密的一種重要手段，它能將一幅自然圖像通過特定數學規則改變像素位置關系或像素值，使其變得雜亂無章無法識別,從而掩蓋內容。盡管研究人員提出了大量圖像置亂算法，但較少關注算法的變尺度置亂能力，在處理非等長的矩形圖像時，這些算法并不能很好地發揮作用。

本文主要貢獻在于：采用基于四方定理的圖像分塊規則，有效解決了已有算法變尺度置亂能力不足的問題。同時，引入分塊置亂、拼接、轉置以及改變形狀等操作，顯著降低了相鄰像素的相關性，置亂程度獲得了提高。仿真結果表明了本文算法的有效性和安全性，能對矩形圖像進行置亂與恢復，置亂效果良好，具有一定的可擴展性。

2 相關工作

研究人員提出了許多圖像加密算法[5 - 7]，主要分為7類，包括基于現代加密體制的圖像加密算法[8]、基于神經網絡的圖像加密算法[9]、基于混沌的圖像加密算法[10]、基于壓縮的圖像加密算法[11]、基于盲源分離的圖像加密算法[12]、基于變換域的圖像加密算法[13]和基于置亂的圖像加密算法。

置亂以其研究的廣泛性、使用的靈活性及加解密的高效性在圖像加密應用中受到青睞。置亂最早起源于經典的加密理論和電視圖像應用技術，主要用于加密圖像內容和作為信息隱藏預處理。Arnold變換[14]、拼圖變換、灰度變換、斐波那契變換[15]、格雷碼、元胞自動機、幻方變換[16，17]、約瑟夫環變換[18]、混沌映射[19]、騎士巡游[20 - 22]及面包師變換是圖像加密中比較常用的圖像置亂算法，都具有實現簡單和處理速度快等特點。其缺點亦較為明顯，變尺度置亂能力較差，通常受限于圖像固定的尺度空間，一般而言只能加密正方形圖像

為克服上述算法變尺度置亂能力不足的缺點，研究人員進行了大量改進。孔濤等[23]對矩形圖像填充部分行或者列，將其擴充為正方形；陳曦等[24]通過插值調整圖像為正方形，但可能導致圖像內容發生形變；胡薇薇等[25]將基于迭代函數系統的圖像置亂方法由2n×2n拓展為N×N。然而這些處理方法會增加計算量與存儲空間。上述研究從改變圖像形狀入手，還有一些研究從修改算法以適應圖像角度展開。Qi等[26]提出用多維等長Arnold變換和Fibonacci-Q變換處理非等長圖像，不需進行擴充等操作；Yang等[27]提出基于Arnold變換對稱性的數字圖像置亂技術，將L×H(L≥H)圖像劃分成多個H×H正方形圖像塊進行置亂，之后再還原為原始圖像大小；邵利平等[28]提出二維非等長的Arnold置亂算法，適用于矩形圖像；李永逵等[29]找到并證明了對任意高寬的數字圖像都存在置亂變換周期的變換矩陣，可廣泛應用于對任意尺寸數字圖像的置亂變換過程；吳成茂[30]提出將二維非等長 Arnold 變換進行非仿射化修改,獲得一種具有非線性變換特性的保面積且具有周期的置亂變換；Hu等[31]采用三維Hilbert曲線，將其基本單元擴展后應用于矩形圖像置亂，避免了圖像擴展缺陷的同時增強了置亂效果。這些算法通常基于Arnold進行改進，雖然沒有增加傳輸加密圖像的負載，但算法實現較為復雜，且推廣至其他算法存在困難。常用的解決方法是將圖像進行分塊，然而問題并未妥善解決。當圖像長與寬的比值不為整數時，如不加密剩余部分則可能會導致信息泄露，若在圖像邊緣填充零再加密，則會改變圖像大小，在進行統計分析時容易被發現[21]。四方定理[32]為該問題的解決提供了便利，它能對任意大小的矩形圖像分塊且圖像塊正好為正方形，而正方形圖像塊能被幻方、騎士巡游、Arnold等方法置亂。因此，本文結合四方定理和幻方置亂，對矩形圖像置亂的問題進行研究。

3 基于四方定理與幻方的矩形圖像置亂算法

基于四方定理與幻方的矩形圖像置亂算法的核心思路為：首先利用四方定理將矩形圖像分為4個正方形圖像塊，解決幻方置亂算法局限于固定尺度的問題。再對各塊進行幻方置亂、拼接，將圖像恢復為原始圖像大小。在整個算法中，采用轉置、改變形狀、多次置亂的方式，進一步提高幻方置亂程度，增強置亂效果。

3.1 基于四方定理的圖像分塊方法

四方定理可將一個自然數分解為4個自然數的平方和，如下所示。

四方定理設有一個自然數N，存在4個正整數a,b,c,d，滿足式(1)：

N=a2+b2+c2+d2

(1)

四方定理的分解并不唯一，例如:

211=82+72+72+72=112+72+52+42

四方定理用于圖像分塊時，和其他預處理方法相比，優勢在于能將圖像分為4個正方形圖像塊且復雜度較小。圖1為基于四方定理的圖像分塊方法示意圖。先對像素總數N進行分解，再取對應數量的像素，即可實現分塊。

Figure 1 Image block based on the four-square theorem圖1 基于四方定理的圖像分塊

3.2 基于幻方的置亂規則

3.2.1 幻方定義與性質

幻方性質特殊，其數學定義為：n階幻方的各行、各列和對角線的數字之和正好相等[33]，其值S=n(n2+1)/2稱為幻和。

根據階數特點，若n為奇數，則稱該幻方為奇數階幻方；若n為偶數，則可分為單偶數階幻方和雙偶數階幻方2種情況，前者n=4k+2,k=0,1,2,…，后者n=4k,k=1,2,…。

3.2.2 幻方的生成

3種幻方生成方法[33]并不同。通常，奇數階幻方構造算法有樓梯法[34]、loubere法、錯位補角法及馬步法[35]；雙偶數階幻方構造算法有Spring法[36]、環形平移補空法及Strachey法；單偶數階幻方構造算法有Strachey法[37]。注意，不同幻方生成算法獲得的幻方存在差異，因而本文為確保幻方的唯一性，采用loubere法生成奇數階幻方，采用Strachey法生成單偶數階幻方，采用Spring法生成雙偶數階幻方。

3.2.3 基于幻方的圖像置亂規則

幻方置亂的缺陷在于：無法處理高與寬不等的矩形圖像；置亂參數較少，加密密鑰空間較小；經過多次幻方變換迭代后的圖像，相鄰像素之間仍然存在較強的相關性，算法安全性明顯降低[17]。為增強置亂效果，有研究人員嘗試將幻方置亂與其他一些技術如分塊壓縮感知[17]、信息光學技術[38]和位運算[39,40]結合。

假設灰度圖像大小為n×n，記為In×n。傳統幻方置亂算法[39]將圖像In×n與n階幻方A的行列一一對應后，按照式(2)進行變換。

(2)

即得到變換矩陣A1，將In×n中元素相應移動得到置亂一次的圖像。同理可得到Ai(i為迭代變換次數)。不難發現，傳統幻方置亂算法存在置亂周期，置亂n2次后恢復為原始圖像，此時置亂失效，算法安全性降低。

3.3 FMSS算法

本文提出了一種四分塊幻方置亂FMSS(Four-block Magic Square Scrambling) 算法，其思路如下：設原始圖像大小為H×W，像素總數可分解為a,b,c和d4個整數的平方和。根據排列組合共有4!=24種分塊方式，默認使用(a2,b2,c2,d2)組合。接著生成所需幻方，對各個圖像塊進行幻方置亂，再將塊拼接恢復成H×W的圖像。常用的多次置亂方法有2種:(1)直接在分塊的基礎上繼續進行置亂再拼接；(2)在圖像塊置亂后，拼接成原始大小的圖像，將其轉置并改變形狀(reshape),使其恢復為原始大小，再進行分塊置亂。由于方法(2)通過轉置和改變形狀使像素在多次置亂中被分配至不同圖像塊中，從而打破了圖像塊之間的壁壘，可充分進行置亂，進而消除塊效應[41]。為增強安全性及置亂效果，本文采用方法(2)進行多次置亂。最后重復上述過程直至達到置亂次數后輸出置亂圖像。需要注意的是，此時變化形狀得到的圖像與之前轉置獲得的圖像不同，形狀變化如下所示：

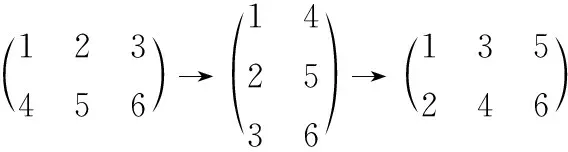
圖2給出了FMSS算法流程，具體描述如算法1所示：

算法1四分塊幻方置亂FMSS算法

輸入：灰度明文圖像大小為H×W，置亂次數t，圖像塊的分解方式及排列組合順序，如：a,b,c,d。

輸出：灰度置亂圖像大小為H×W。

步驟1根據輸入圖像尺寸，采用四方定理將圖像分為4個正方形塊(I1,I2,I3，I4)。

步驟2根據正方形圖像塊尺寸，使用幻方生成算法生成幻方矩陣組合(M1,M2,M3,M4)。

步驟3使用(M1,M2,M3,M4)依次對每個圖像塊執行幻方置亂，獲得置亂圖像塊(I′1,I′2,I′3，I′4)。

步驟5若當前置亂次數小于t，則繼續對S3執行步驟3和步驟4。

步驟6輸出置亂圖像S。

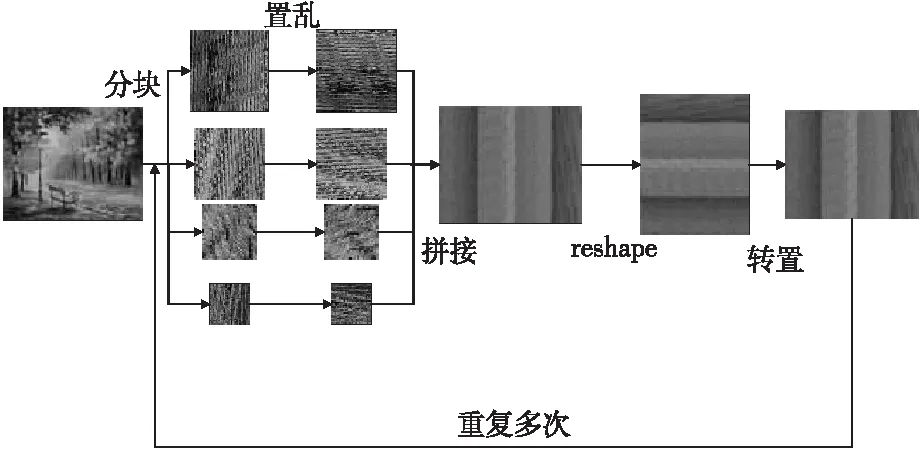
Figure 2 Flow chart of FMSS algorithm圖2 FMSS算法流程圖

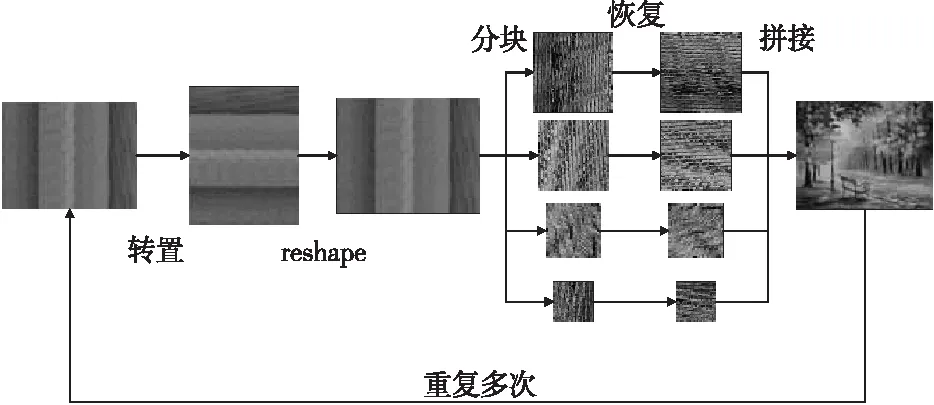
Figure 3 Flow chart of FMSS recovery圖3 FMSS恢復流程圖

Figure 4 Image scrambling and recovery results圖4 置亂與恢復結果

在FMSS算法中，置亂、分塊、拼接、轉置及形狀變化均可逆，因而置亂圖像可被恢復為原始圖像，且恢復過程與置亂過程相反。圖3給出了置亂圖像恢復的流程圖，因篇幅限制不再贅述。

4 實驗與結果分析

為測試FMSS的有效性，本節進行了多組仿真實驗，以檢驗置亂圖像相鄰像素間的相關性、抵抗各種攻擊的魯棒性以及置亂和恢復的速度。

實驗運行環境：64位Windows 10操作系統，平臺為Matlab 2014a，16 GB內存，CPU為Intel 酷睿i7-8750H 2.2 GHz。仿真實驗所用圖像為USC-SIPI圖像數據集[42]以及Matlab圖像處理標準圖像庫中的Green(500×300)、Football(320×256)和Lena(256×256)圖像，均為bmp格式的圖像文件。

4.1 置亂圖像結果

四方定理有效解決了幻方置亂的變尺度置亂能力不足問題，使得待置亂圖像不再局限于方形圖像。為檢驗實際效果，本節利用Football和Green等矩形圖像進行實驗驗證。設置亂次數t∈[1,100]，將FMSS算法置亂后的圖像保存。圖4展示了矩形圖像置亂1次和100次的結果。可以看到，使用FMSS算法置亂1次后的圖像出現明顯的條痕現象。這是因為圖像分塊置亂次數不足導致塊與塊之間差異明顯。然而，隨著置亂次數的增加，該現象徹底消失。置亂100次時，圖像充滿隨機的噪點，無法從直觀上觀察到該圖像與原始圖像存在任何聯系。此時置亂圖像完全掩蓋了原始圖像，且又能恢復為原始圖像。由此可知FMSS算法可對非等長圖像進行置亂，突破了幻方置亂的局限，增強了幻方置亂算法的變尺度置亂能力，置亂圖像具有不可識別性和噪聲性，這表明該算法具有良好的置亂和恢復效果。

此外，為驗證FMSS算法與其他針對正方形圖像的置亂算法相比在圖像置亂上效果的優勢，本節還使用FMSS算法對正方形圖像進行了測試。對比實驗采用了騎士巡游置亂[20]和幻方置亂[39]。原始圖像采用Lena圖像，所有算法置亂次數均設置為100，實驗結果如圖5所示。圖5a表明，在提升置亂效果方面，FMSS算法的優勢更加明顯；圖5b和圖5c表明，使用騎士巡游置亂和幻方置亂的結果保留了一定的原始圖像細節信息，未充分置亂，置亂效果不滿足加密要求。

Figure 5 Scrambling results of square images圖5 正方形圖像置亂結果

上述實驗結果表明,FMSS算法對矩形圖像置亂是有效的，增強了幻方置亂算法變尺度能力，且圖像置亂效果良好，顯示了FMSS算法的可行性與優勢。

4.2圖像分塊對置亂的影響

毫無疑問，分塊的方式、數量將對置亂圖像產生一定的影響。原始圖像采用Lena，利用經典幻方置亂算法[39]進行對比實驗，置亂次數t∈[1,100]。圖6給出了實驗結果。

相比于幻方置亂算法，FMSS算法采用的分塊方法明顯提升了圖像置亂效果。原始幻方置亂算法置亂不充分，大量原始圖像細節信息被保留,增加置亂次數也未能緩解該不足。在置亂次數較少時FMSS算法置亂圖像出現明顯條紋，隨著置亂次數t的增加，圖像充滿隨機噪點，整體趨于混亂。這是因為首次置亂之后再拼接會存在較為明顯的痕跡，分塊作用隨著置亂次數的增加逐漸顯現，塊之間的像素充分交換，圖像混亂程度加深。

Figure 6 Effect of block on image scrambling圖6 分塊對圖像置亂的影響

另外，FMSS算法的分塊過程可繼續遞歸進行，例如將圖像進一步劃分為16塊、64塊，甚至更多。為檢驗FMSS算法分塊數量對圖像置亂的影響，依舊采用Lena圖像，將圖像分為數量不同的塊，依次設分塊數量bn為4,16,64，設置置亂次數t∈[1,100]。圖7給出了實驗結果。不難發現，在置亂次數t較低的情況下，不同分塊數量的置亂圖像存在明顯差異。置亂次數t為1時，分塊數量bn越多，條紋越明顯；t為5時，該現象得到一定程度緩解；t為10時，條紋基本消失，分塊數量的影響幾乎相同；t為100時，基本無區別。

由實驗結果可知，分塊一方面增強了幻方置亂變尺度置亂能力，同時也獲得了更好的置亂效果。圖像分塊的數量僅在置亂次數較少時有顯著作用，當置亂次數增多時，置亂效果互相接近。因此，可將分塊數量合理地設置為4，在不影響置亂效果的前提下加快FMSS算法置亂與恢復的速度，降低時間復雜度。

4.3 相鄰像素點的相關性分析

自然圖像在水平、垂直及對角線方向上的相鄰像素通常具有較高的相關性。研究人員常利用該統計特性分析加密圖像的算法，所以在一定程度上，相關性代表著加密算法的安全性。安全性高的加密算法能夠有效降低圖像相鄰像素的相關性。

Figure 7 Influence of block numbers on image scrambling圖7 分塊數量對圖像置亂的影響

嚴格的相關系數定義如式(3)～式(5)所示：

(3)

(4)

(5)

其中，x和y表示選中的相鄰像素序列，xi和yi表示x,y中的第i個像素的像素值，樣本數量為K，x的期望和方差分別為E(x)和D(x)。一般而言，當相關系數絕對值大于0.8時，相鄰像素間存在較強的相關性;當相關系數絕對值小于0.3時，相鄰像素間的相關性較弱。

FMSS算法引入了圖像拼接、分塊、轉置與改變形狀等操作，所有像素在多次的分塊、拼接過程中被充分打亂，有效破壞了相鄰像素的位置關系。為驗證上述操作在降低圖像相鄰像素相關性和提升安全性上的表現，本節采用Green圖像作為明文圖像，設置不同的置亂次數，分別從水平、垂直和對角線方向隨機選取200行200列進行仿真分析，進行200次相同操作，取200次實驗結果的平均值，結果如表1所示。

Table 1 Correlation coefficient between adjacent pixels of plain image and scrambling image

在水平和垂直方向上，明文圖像相鄰像素相關系數絕對值在0.88附近，而對角線方向為0.78左右，表明相關性較強。當置亂次數t從1增加到100時，置亂圖像相鄰像素相關系數接近0，與原始圖像相比下降約80%，表明FMSS算法具有較好的安全性，可有效抵抗統計分析。

為進一步分析FMSS算法的安全性，從Green置亂圖像中隨機選取1 000個點，分別繪制了3個方向的相關性圖，如圖8所示。從圖8a～圖8c可看到，明文圖像樣本均分布于對角線兩側，表明相關性較強，而置亂圖像圖8d～圖8f的樣本則隨機散布在整個空間中，相鄰像素間相關性顯著降低，說明置亂100次后圖像像素之間關聯非常小。同時這也表明置亂圖像具有較高的混亂程度和較好的安全性。

Figure 8 Experimental results of image correlation analysis圖8圖像相關性分析實驗結果

由此可知，FMSS算法顯著降低了相鄰像素間的相關性，能夠抵抗統計攻擊，具有較好的安全性。考慮到FMSS算法的分塊、拼接、轉置、改變形狀及置亂并未改動任意像素的像素值，因此不會對圖像直方圖做出任何改變。

4.4 魯棒性分析

數據在傳輸過程中可能會有噪聲，因此置亂要求能抵抗一定的攻擊和分析，包括壓縮圖像、裁剪圖像及添加噪聲等攻擊。由于置亂圖像經過了拼接、分塊和轉置，所以鄰域相關像素分散比較均勻，因而可以抵御剪切、擦除等常規圖像攻擊。

峰值信噪比PSNR(Peak Signal to Noise Ratio)和歸一化相似度NC(Normalized Correlation)等評價指標能夠客觀反映被攻擊后的圖像質量，常被用于評價魯棒性，其嚴格的數學定義如式(6)～式(8)所示：

(6)

(7)

(8)

其中,明文圖像(i,j)位置的像素值為W(i,j)，恢復后該位置的像素值為W′(i,j)，MAX=255，H和W分別為圖像的高和寬。NC取值為[0,1]，越接近1，表明恢復圖像越接近明文圖像；PSNR值越大，說明恢復圖像質量越高。通常PSNR低于30 db表示恢復圖像劣化嚴重。

為檢驗抗噪聲攻擊及剪切的魯棒性，本節采用Green和Lena圖像，對圖像添加椒鹽噪聲和進行剪切攻擊。部分Lena被攻擊圖像與恢復圖像如圖9所示，表2給出了所有實驗結果。

不難發現，在添加少量椒鹽噪聲時，圖9a和圖9b的圖像恢復受到了輕微影響;圖9c和圖9d的恢復圖像中噪點充滿整幅圖像;圖9e～圖9g能獲得圖像大部分信息，NC值高于0.9;而圖9h則嚴重劣化，PSNR值很低，NC值下降至0.8附近。

剪切攻擊圖像(圖9i～圖9p)表明，圖像質量劣化程度隨著剪切比例的增大而加深。剪切左上角1/16(6.25%)圖像時，剪切攻擊造成的影響被FMSS算法均勻分散，圖像質量輕微劣化，可通過濾波去噪技術將噪點濾除，進而提高恢復圖像質量。而圖9j和圖9k的NC值和PSNR值接近，這表明裁剪程度一定時，裁剪位置產生的影響較小，有損攻擊被均勻分散到圖像各個位置。不難發現，此時恢復圖像質量劣化程度進一步加深，仍可以觀察到圖像輪廓信息。當裁剪一半圖像時，恢復圖像丟失大部分信息，圖像質量存在非常嚴重的劣化，視覺感官上難以接受。

Table 2 Experimental results of salt & pepper noise and shear attack

表2數據表明，受到噪聲攻擊時，不同圖像的恢復圖像質量接近。面對噪聲攻擊，Lena圖像與Green圖像的PSNR值接近但后者略低(Green圖像未在圖9中展示)。NC值在噪聲較少時接近，差距隨著椒鹽噪聲量增大而逐漸增大。面對剪切攻擊，Lena圖像與Green圖像的PSNR值差距較小，但Green圖像的略高，NC值基本一致。由此可知，與經典的幻方置亂算法相比，FMSS算法具有較好的魯棒性，有損攻擊被均勻分散，抗噪聲和裁剪能力得到顯著提高。

Figure 9 Experimental results of salt & pepper noise and shear attack圖9 椒鹽噪聲與剪切攻擊實驗結果

此外，由于JPEG格式圖像在互聯網上傳輸使用相對更為廣泛，而仿真實驗采用BMP格式圖像，為了檢驗和擴展FMSS算法的實用性，本節還進行了JPEG有損壓縮攻擊實驗。實驗使用Green圖像，設FMSS置亂次數t為100，表3給出了實驗結果。

顯然，PSNR值和NC值隨著壓縮因子遞增而增大，恢復圖像質量越來越高。壓縮因子較低時，恢復圖像與原始圖像的NC值仍然較大。這表明即使是受到一定程度的JPEG壓縮，存在一定的失真情況，恢復圖像質量仍然較高，圖像輪廓依然清晰可見。總體而言,JPEG壓縮并不會影響置亂圖像質量，這說明FMSS算法具有較強的抗JPEG有損壓縮的能力，滿足實際應用要求。

由前述實驗結果不難得知，FMSS算法通過位置置亂有效分散了錯誤像素，椒鹽噪聲、剪切和JPEG壓縮等攻擊對FMSS算法影響有限。因此，FMSS算法具有良好的魯棒性，較之傳統幻方置亂算法有所增強，可在實際網絡環境中應用。

Table 3 Experimental results of JPEG compression attack

4.5 運行時間分析

因為圖像置亂和恢復過程互為逆向，因而在理論上置亂和恢復的時間開銷基本一致。為檢驗算法置亂和恢復時間，對Lena、Football和Green圖像采用FMSS算法分別進行10次置亂，表4給出了置亂20次和恢復所用的時間平均值、最大值和最小值。從表4可以看出，FMSS算法置亂與恢復所用時間相差無幾，且置亂所用時間與圖像像素總數成正相關。還可以看出，FMSS算法具有較快的置亂和恢復速度，其原因在于，幻方生成算法判斷、循環語句及移動元素操作較少，時間復雜度相對較低，因而FMSS算法置亂與恢復較快。

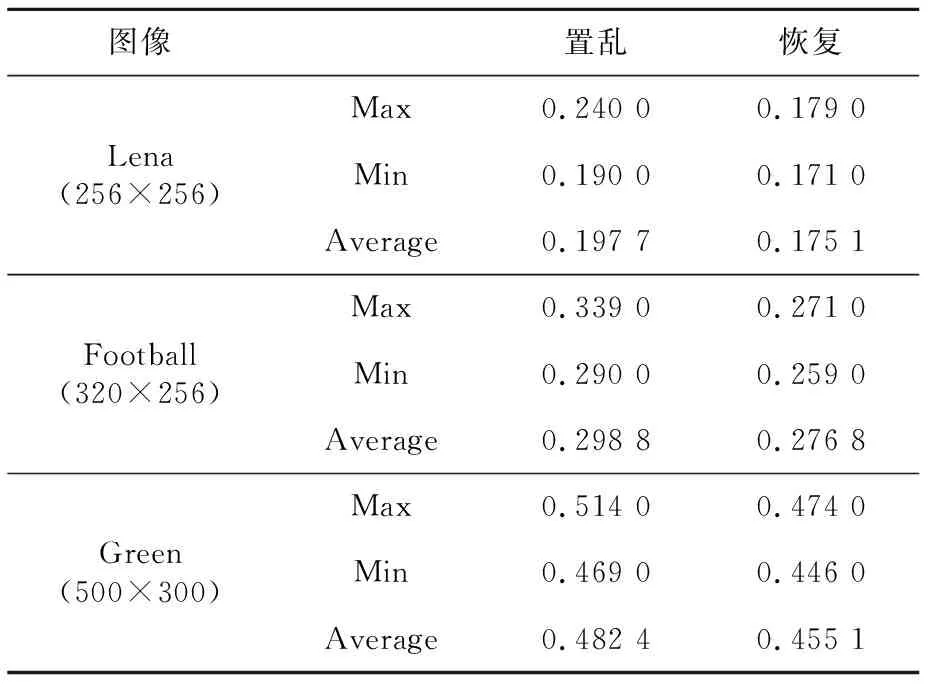
Table 4 Image scrambling and recovery time

5 結束語

本文基于四方定理和幻方置亂，提出了一種新的矩形圖像置亂算法FMSS。首先，該算法根據明文圖像的尺寸使用四方定理將圖像劃分成4個正方形圖像塊;其次，利用幻方生成算法生成所需大小的幻方，并按約定的順序對每個圖像塊分別進行幻方置亂；最后，將置亂后的圖像塊按順序拼接成圖像，恢復為原始圖像大小。在整個算法中，采用多次置亂處理以增強置亂效果。恢復圖像過程為上述過程的逆過程。FMSS算法能夠快速處理矩形圖像，具有良好的置亂效果。仿真實驗結果表明，分塊、拼接、轉置及變換形狀等操作顯著消除了圖像相鄰像素間的相關性，相比傳統幻方置亂算法，密鑰空間較大，還增強了變尺度置亂能力、魯棒性與安全性。本文的工作拓展了幻方置亂算法的應用范圍，為數字圖像置亂研究提供了一條新途徑。在本文工作基礎上，值得進一步拓展研究之處包括：

(1) 測試所提置亂算法周期性。FMSS算法引入了分塊、拼接、轉置和變化形狀等操作，同一像素點每次所在圖像塊不固定，從而使得置亂圖像周期性出現的可能性大大減小，一定程度上提高了安全性。當前仍需要足夠的測試驗證并完善算法的安全性。

(2)將FMSS算法擴展應用于局部圖像置亂。 在某些應用場景下，僅需要對局部圖像進行處理。因此，可對FMSS算法進一步完善，即可用于實際局部圖像置亂，提高其實用性。

(3)將FMSS算法擴展應用于要求明文圖像為正方形的置亂處理中，與Arnold置亂算法、斐波那契置亂算法、騎士周游置亂算法等融合研究，并應用于視頻、音頻加密處理。