基于優化K-P-Means解混方法的高光譜圖像礦物識別

孫 肖， 徐林林， 王曉陽， 田 野， 王 偉， 張中躍

(1.中國地質調查局廊坊自然資源綜合調查中心，廊坊 065000； 2.中國地質大學(北京)土地科學技術學院，北京 100083)

0 引言

高光譜遙感具有“圖譜合一”的特點，已廣泛應用于礦物識別、固體礦產和油氣勘探、環境保護及環境監測、植被分類及檢測、月球和行星探測等方面[1-2]。現有高光譜遙感礦物識別技術主要采用基于礦物波譜曲線的光譜匹配技術，如混合像元分解技術、光譜角技術和混合調制匹配濾波技術等[3-5]。混合像元分解技術是一種常用的高光譜礦物識別技術。由于成像光譜儀的硬件問題，高光譜遙感圖像普遍光譜分辨率高而空間分辨率低，容易導致影像像元出現同譜異物現象，因此必須研究解混方法予以克服。

目前常用的解混方法包括像元純凈指數、N-Findr、頂點成分分析、最小二乘端元提取算法等[6-9]。在前人工作的基礎上，Roberts等[10]提出了經典的迭代光譜解混方法(MESMA)； Asner等[11]引入蒙特卡洛理論，將其與迭代解混理論有效結合起來，提出了AutoMUC方法； Song[12]介紹了一種基于貝葉斯決策的BSMA方法； 吳柯等[13]提出了基于神經網絡的端元可變解混方法； 林紅磊等[14]提出基于單次散射反照率的礦物高光譜稀疏解混方法。上述高光譜解混方法雖然反演精度有了很大的提高，但是經典的方法大都依賴于純凈像元，由于圖像的空間分辨率和地表目標的復雜程度，純凈的像元是很難直接從高光譜圖像中獲取的； 此外，這些方法在解釋混合像元的成像機理方面也還不完善。

Xu等[15]利用線性光譜混合模型來解釋混合像元的成像機理，利用凈化像元的概念提出K-P-Means算法來進行高光譜混合像元分解。該算法分2步迭代(豐度估計和端元優化)，通過基于高斯混合模型的期望最大(expectation maximization，EM)估計算法直到最終的端元估計收斂。由于K-P-Means算法估計端元和豐度的能力較強，因此，本文將該算法應用于礦物識別。該算法端元的優化借助于計算出的地物類別標簽，由于地物類別標簽可能不正確，導致計算出的凈化像元存在多個類別，這種現象會導致端元優化不理想。Fischler等[16]提出的隨機抽樣一致性算法(random sample consensus，RANSAC)，可以有效剔除因分類標簽不正確導致的凈化像元中的異常值的影響。因此本文提出基于RANSAC的穩健的K-P-Means算法(RANSAC based robust K-P-Means，RR-K-P-Means)。在K-P-Means算法的基礎上，利用RANSAC算法剔除異常影響，提高端元優化的精度。最終將該算法用于美國內華達州銅礦區的AVIRIS高光譜傳感器Cuprite數據的礦物識別，將估計出的光譜曲線與美國地質調查局網站提供的礦物波譜曲線進行匹配，確定礦物種類。

1 高光譜混合像元分解方法

1.1 基本原理

1.1.1 線性光譜混合模型

線性光譜混合模型是一種常用的高光譜遙感圖像表達方式[17]。假設高光譜圖像像元集X由端元矩陣A和豐度矩陣S以及獨立同分布的高斯噪聲N組成，即

X=SAT+N，

(1)

(2)

(3)

式中：si(i=1,2,…，m)為E×1的豐度向量，用來表達第j個端元光譜向量aj(j=1,2,…,E)在P×1維高光譜像元xi中的貢獻；m為圖像像元個數；E為端元個數；P為波段數；n為高斯噪聲向量。

1.1.2 K-P-Means模型

由于同一類的混合像元允許多種端元存在，為了更進一步移除豐度值較低的端元的影響，使用豐度值最大的端元(而不是用整個xi)來估計aj是很合理的。Xu等[15]把移除豐度值較低端元貢獻后的xi稱為凈化像元。

K-P-Means模型是傳統K-Means模型的衍生，考慮到實際中豐度非負，因此算法可以表述為：

(4)

式中k為地物類別數。

相比K-Means考慮物理過程的整體效果，K-P-Means探究影響觀測的物理過程的源頭，其目標函數可以表述為:

(5)

(6)

式中：l為類別；yi為第k類的凈化像元向量。

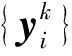
基于上面描述的模型，由于未知數遠遠多于觀測方程的個數，這是一個嚴重奇異的問題。EM算法對于奇異問題的參數求解具有較好的效果，該算法通過迭代的方法尋找統計模型的最大似然估計[18]。K-P-Means模型依據EM算法分2步迭代進行豐度估計和端元優化： 首先,通過非負最小二乘法進行豐度的估計; 然后,通過計算的豐度對端元進行優化。

1.1.3 豐度估計

給定{aj}，假設噪聲滿足高斯分布模型，則其噪聲的概率密度函數p(n)為：

(7)

(8)

估計豐度的目標函數可以表達為：

(9)

由于方差可以通過均勻區域法獲取，并作為權重計算豐度，地物類別li通過sik最大確定，即

(10)

因此，式(9)中豐度的估計本質上就是一個加權非負最小二乘(weight nonnegative least square， WNNLS)問題[19]。

1.1.4 端元優化

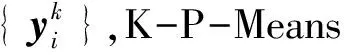
(11)

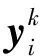
1.2 RR-K-P-Means算法

從上述K-P-Means算法的原理很容易發現，端元的優化完全依賴于由豐度確定的標簽。類別標簽錯誤或者存在異常值都會導致端元的優化精度降低。實踐過程中，從凈化像元值的直方圖可以明顯發現存在多個類別(圖1)。

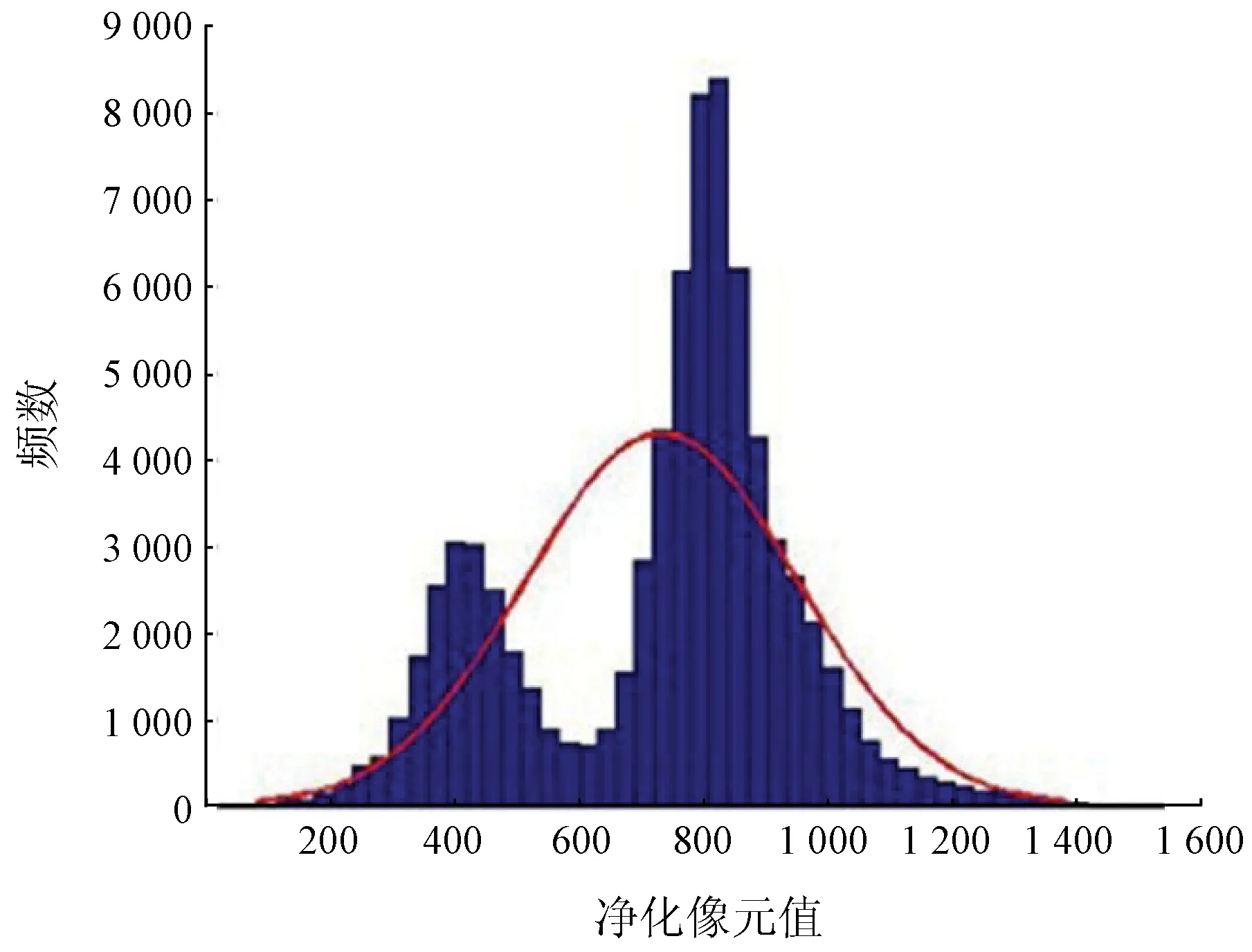
圖1 凈化像元直方圖Fig.1 Histogram of purified pixels

凈化像元值存在多個類別的現象降低了利用K-P-Means算法進行混合像元分解的精度。在計算機視覺以及其他很多研究領域，RANSAC算法對錯誤率超過50%的數據仍然能夠得到理想的處理結果，是最有效的穩健估計算法之一[20]。因此，本文利用RANSAC算法對K-P-Means算法混合像元分解過程中產生的凈化像元進行優化，剔除錯誤標簽的影響，實現對K-P-Means算法的優化。

基于RANSAC算法的穩健的K-P-Means算法基本過程可以描述為： ①利用式(1)—(10)原理獲取帶有錯誤標簽的凈化像元； ②尋找一個模型(一般為線性模型)適應于假設的正確的凈化像元(初始采用隨機點)，利用尋找的凈化像元估算該模型的參數(圖2)； ③用第二步得到的模型去測試所有的其他端元，若某個端元適用于估計的模型，則認為它也是該類別的端元，其他端元滿足的條件設置為大于最小端元差值(設定閾值)，如果有足夠多的端元被歸類為假設的正確類別的端元，那么估計的模型就足夠合理，用所有假設的正確的端元去重新估計選取的模型，直到估計的正確的端元數量滿足給定條件(設置最低錯誤率)為止； ④重復第二步和第三步過程來估計更加穩健的參數，選擇更加合理的端元，將獲取的合理的端元帶入式(11)，獲取優化后的端元。

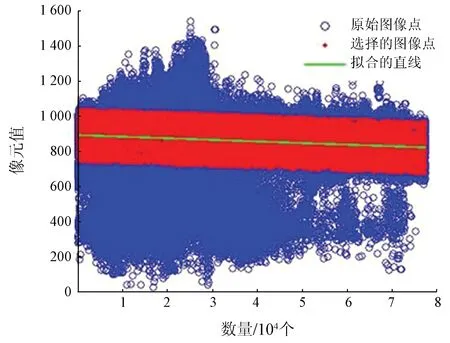
圖2 基于RANSAC算法的端元優化原理示意圖Fig.2 Schematic diagram of the principle of end-memberoptimization based on RANSAC

2 實驗與結果

2.1 仿真數據實驗

從美國地質調查局公布的地物光譜庫中，隨機選擇4條地物光譜曲線，按照如下程序混合成64×64大小的圖像。利用這4個端元，首先把整個圖像分成8×8的同質塊； 然后通過7×7窗口大小的空間低通濾波對這些同質塊降級； 再通過添加零均值高斯噪聲對圖像再降級，從而獲取和真實情況更為接近的仿真數據。

豐度和端元的估計實驗中，如果2個端元估計值的光譜角度距離(spectral angle distance，SAD)小于一個給定的數值τ或者預先規定迭代的次數iters，那么2步迭代就停止。本次實驗中τ=0.01，iters=50。每次迭代中采用頂點成分分析的結果作為端元的初值[8]。利用RR-K-P-Means算法對端元進行優化時，模型采用線性模型，其他端元距離該直線的最小端元差值設置為5，最低錯誤率設置為15%。

分別利用K-P-Means算法和RR-K-P-Means算法進行豐度和端元的估計。用廣泛使用的SAD和光譜信息散度(spectral information divergence, SID)來評價估計端元和真實端元的一致性[21]。為了便于表示，將SID的數值統一擴大10 000倍。利用結構相似性(structural similarity，SSIM)和峰值信噪比(peak signal-to-noise ratio，PSNR)來衡量利用估計的豐度和端元重新獲得的圖像與原圖像的相似性[22-23]。

SAD和SID值越小，估計的光譜曲線與真實光譜曲線越相似。SSIM和PSNR越大，表明利用估計的豐度和端元重新獲得的圖像與原始圖像越相似。從表1中數據可以看出，利用RR-K-P-Means算法估計的端元和豐度SAD達到0.73，SID達到3.1，估計值和真實值的一致性分別提高8.8%和13.89%。

表1 優化前后圖像各指標對比Tab.1 Comparison of image parametersbefore and after optimization

利用估計的端元和豐度重新獲取的圖像和原始圖像相似性SSIM達到0.997，PSNR達到35.67，相似性分別提高10.17%和62.80%。RR-K-P-Means算法明顯優于傳統的K-P-Means算法。從PSNR來看，RR-K-P-Means算法能更好地減弱噪聲對估計的影響。

RR-K-P-Means算法可以剔除個數較少的異常類別的影響，而且選擇的數據符合數據的分布形式(圖3)。盡管RR-K-P-Means算法不能在大范圍上改善分類結果，但是在細節上相比K-P-Means算法有了很大的改善。RR-K-P-Means算法估計的端元和豐度如圖4所示。圖4(a)—(d)為4種地物端元的估計值和真實值，兩者吻合程度比較高； 圖4(e)—(h)和(i)—(l)分別為4種地物的真實豐度和估計豐度，說明本文算法可以很好地計算豐度。較高精度的端元和豐度估計結果，為后續的礦物識別做好了準備。

圖3 真實標簽與優化前后2種算法確定的地物標簽

圖4 優化后估計的端元、豐度與真實值對比

2.2 真實高光譜數據

將RR-K-P-Means算法用于真實高光譜遙感圖像數據的礦物提取。實驗中采用美國內華達州銅礦區的AVIRIS高光譜傳感器的Cuprite數據集(圖5)，數據獲取網站地址： http: //www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes。Cuprite數據集除了少數植被覆蓋外大部分為含指示礦物的蝕變帶，是進行高光譜遙感地質研究的典型樣區。該影像數據為1997年6月19日機載AVIRIS獲得，包括224個波段，地面瞬時視場約為20 m。剔除水汽影響嚴重的波段，共選取159個波段進行實驗。

圖5 內華達州銅礦區的Cuprite數據集Fig.5 Cuprite data sets of Nevadacopper mining area

利用RR-K-P-Means算法對Cuprite數據集進行端元和豐度的估計，通過計算估計出的端元和美國地質調查局礦物波譜庫的波譜曲線的相關性確定端元所屬的礦物類別。由于實際地物比較復雜，因此實驗中的端元數設置為30，多于本地礦物的種類。選擇相關系數大于0.75的端元進行研究。

通過相關系數的匹配得出8個類別的主要礦物，分別為： 黃鉀鐵礬、水銨長石、玉髓、葉蠟石、綠脫石、綠泥石、蒙脫石和白云母。研究區主要礦物綠脫石的端元估計結果如圖6所示，波長在400～600 nm的端元估計結果和真實值匹配度一致，其他部分基本相同。

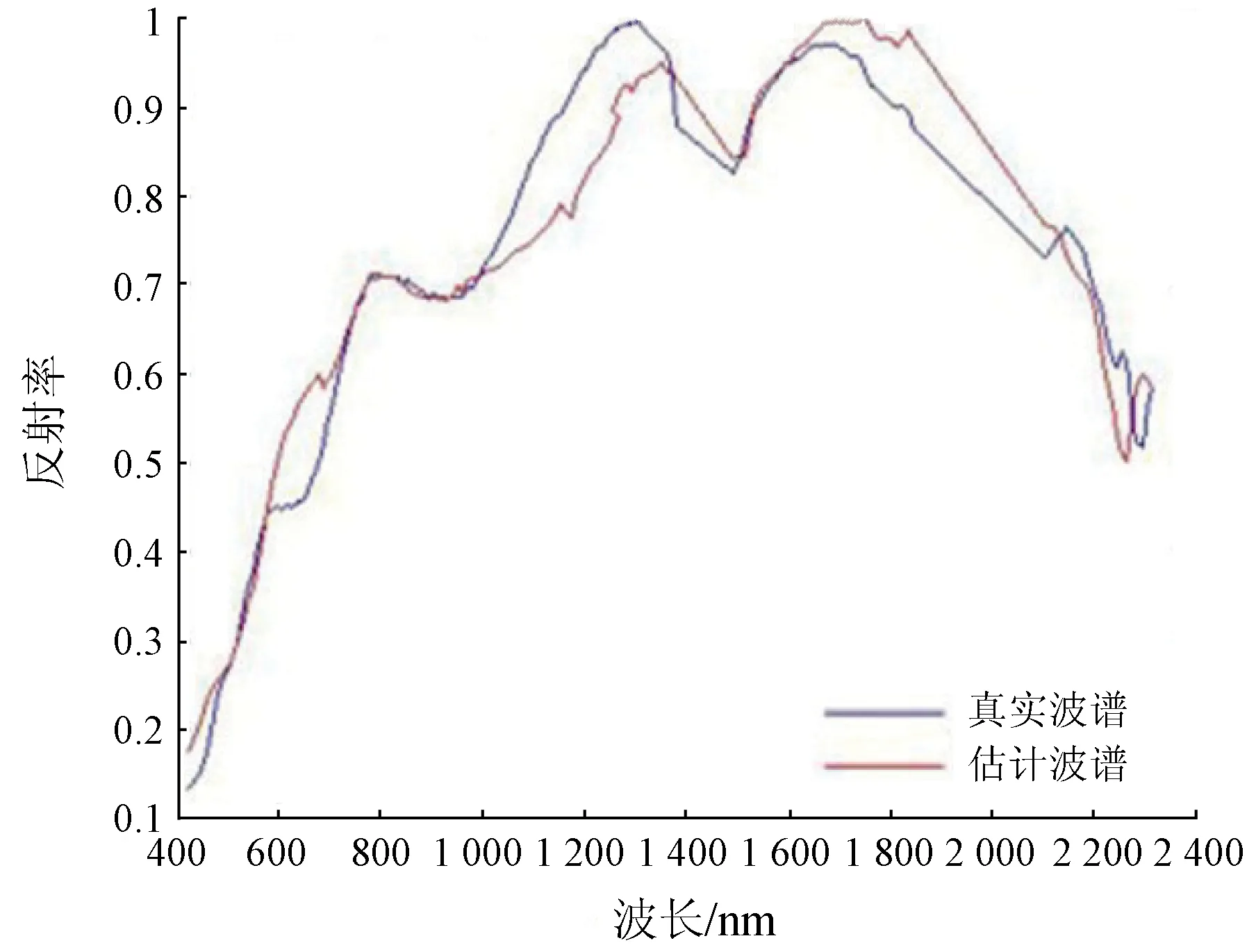
圖6 綠脫石的端元估計值與真實值Fig.6 Estimated and true endmember values of nontronite

研究區主要礦物黃鉀鐵礬的端元估計結果如圖7所示，估計端元波譜曲線與真實值基本相同。在實際應用中，利用RR-K-P-Means算法估計的端元可以有效提取礦物的波譜曲線。

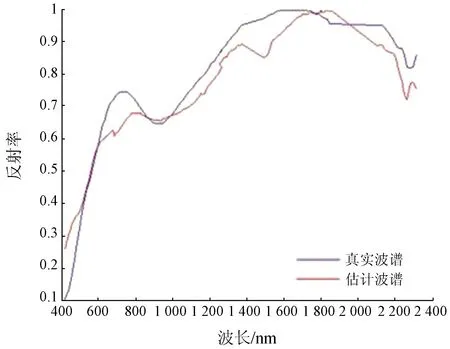
圖7 黃鉀鐵礬的端元估計值與真實值Fig.7 Estimated and true endmember values of jarosite

8種主要礦物的豐度圖見圖8。由圖8可見，礦物聚集性比較好，與已知樣本分布相比較，利用RR-K-P-Means算法獲取的8種主要礦物基本與實際情況一致。

圖8-2 識別出的8種礦物的豐度圖

3 結論

針對K-P-Means算法中端元優化受異常值影響的問題，提出基于RANSAC的穩健的K-P-Means算法(RR-K-P-Means算法)，并將該算法用于礦物識別，通過仿真和真實數據實驗，都取得了理想的效果。得出如下結論：

1)仿真實驗證明，利用RR-K-P-Means算法估計的端元和豐度與真實值的一致性提高明顯。利用估計的端元和豐度重新獲取的圖像和原始圖像相似性提高較多。從PSNR來看，RR-K-P-Means算法能更好地減弱噪聲對估計的影響。本文算法可以剔除個數較少的異常類別的影響，而且選擇的數據符合數據的分布形式。

2)通過真實數據驗證，利用RR-K-P-Means算法可以較好地識別研究區主要礦物，和美國地質調查局地物波譜庫提供的標準地物波譜相比具有較高的一致性。在高光譜遙感圖像礦物識別中，RR-K-P-Means算法可以有效提取多種地物光譜，礦物識別效果較好。

本文端元優化采用算數平均值，豐度較小的標簽未參與計算，未來可以將加權平均的方法應用到本研究中。除此之外，RR-K-P-Means不僅在高光譜遙感圖像礦物識別中可以得到很好的應用，同時可以推廣到分類、去噪、超分辨率重建等研究中。