一種模擬動邊界繞流的銳利界面浸入邊界法*

郭 濤，張晉銘，張紋惠,3，王文全

（1. 昆明理工大學建筑工程學院，云南 昆明 650500；2. 四川大學水力學與山區河流開發保護國家重點實驗室，四川 成都 610065；3. 中國能源建設集團云南省電力設計院有限公司，云南 昆明 650051）

繞流是自然界以及實際工程運用中一個十分普遍的物理現象，也是一個經典的流體力學問題。例如：機翼在流動空氣中的振動問題；導彈無側滑大攻角飛行時，背風面分離渦的不對稱運動導致的附加偏航力問題；水輪機導葉、葉片在水流作用下的擺動和振動問題；魚在水中通過魚鰭的擺尾提供推力；昆蟲利用翅膀的拍動使其在空中飛行等等。這些運動及工程都有涉及到翼型、橢圓在流場中的繞流問題。當流體繞過不具有流線型的鈍體結構時，在鈍體尾部會發生周期性的漩渦脫落，產生周期性的上下拖曳力，也就是升、阻力。隨著來流情況的變化，當渦脫頻率接近結構的自振頻率時，漩渦脫落和結構振動相互鎖定，形成共振，也就是渦激振動，其在實際生活中產生的危害十分常見并且影響也十分廣泛。例如：1940 年剛通車數月的塔科馬大橋發生顫振風毀事件，震驚世界；以及近期的虎門大橋渦激振動事件等。因此，流固耦合問題一直是計算流體力學領域較為關注的一類重要問題。

一般地，研究流固耦合問題時，通常采用貼體網格，這類網格質量良好且生成速度快，但是在實際計算中，為了適應不斷變化的邊界條件，在每一個時間步中都要重新劃分網格，這樣就大大增加了計算成本。鑒于這些原因，Peskin提出了浸入邊界法，并應用到模擬人類心臟血液流動中的瓣膜運動中。浸入邊界法（immersed boundary method，IBM）在整個物理計算區域中采用一套笛卡爾網格，避免了在每一個時間步更新網格的繁瑣，使用力場來代替固體邊界，使流固耦合問題中的動邊界處理起來更加簡單和精確。因此，力源項的獲得是浸入邊界法求解流體問題的關鍵。Peskin 方法，早期是將固體邊界離散為一組由彈簧連接的單元，當邊界發生變形時，就會產生一個意圖使其回到原位置的回復力，通過邊界上的回復力結合delta 函數求得力源項。但該方法涉及到固體的彈性變形，主要適用于柔性體，而且該變形不易通過流場物理量求得，不具有一般性。Goldstein 等在此基礎上發展了虛擬邊界法來求解剛性邊界問題，主要使用反饋力法，配合譜方法來漸進地施加所需的邊界條件，該法也稱反饋力法。在浸入邊界法的發展過程中，Jamaludin 等提出了直接力法，即通過直接構造受力區的速度場來推導力源項，從而確保滿足邊界條件，基本實現了對邊界的準確描述，成為學者們的主要研究方向之一。如Fadlum 等將其應用于流固耦合研究，獲得了與貼體網格下計算結果一致性較好的結果；Le 等提出了一種隱式直接力浸入邊界法，Wu 等、王文全等提出了一種對速度進行二次修正的隱式直接力浸入邊界法；Uhlmann等提出了顯式直接力法。直接力法相比于Peskin 的經典IBM 法，無須通過繁瑣的delta 函數完成拉格朗日點與歐拉點上信息交換，通過直接施加浸入邊界處的速度邊界，由此推導出力源項，不依賴于固體的本構關系，也不進行反饋調整，故名直接力法。

按照是否使用delta 函數或能否對界面進行清晰描述，可將IBM 法分為擴散界面（diffused-interface）浸入邊界法和銳利界面（sharp-interface）浸入邊界法。理論上來講，經典浸入邊界法、反饋力法和直接力法均屬于擴散界面浸入邊界法。銳利界面法不直接計算力源項來施加邊界條件，主要是在界面處通過局部插值，重構邊界網格點附近的流動參數（速度），以此作為邊界條件將其直接施加到計算域進行求解。理論上可以具有高階精度，在可壓縮流體以及激波沖擊問題中均得到了利用。本文將亦采用一種改進的銳利界面浸入邊界法，將整個物理區域劃分成純流體區域以及包含固體的次流體區域。在流體次區域邊界的法向，構造“虛擬點—受力點—垂足點”的計算結構。受力點速度由流體域內某一虛擬點和邊界上垂足點之間的速度線性插值確定,實現復雜動邊界的流動數值模擬。本文利用C++編程，通過圓柱繞流經典算例與其他方法的文獻結果及試驗結果進行對比，驗證該方法的有效性和準確性。基于該方法，進一步探究不同軸長比、不同攻角 θ 下的橢圓柱繞流的渦結構分布特征、流線、壓力等流場現象和升阻力系數、渦脫頻率等水力不穩定現象。

1 銳利界面浸入邊界法求解過程

1.1 控制方程

將整個物理區域（包括流體、固體）看作不可壓縮牛頓流體的粘性流動。在整個計算域內，流體采用Euler 描述，固體采用Lagrange 描述。其連續性方程和動量方程可表示為

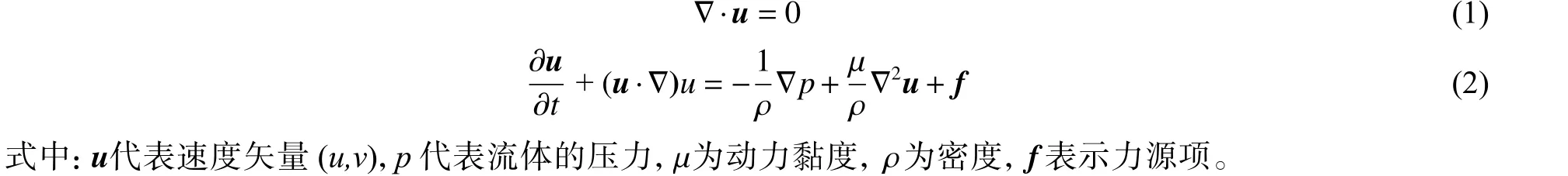
1.2 時間推進

采用二階時間分布投影法對時間進行離散，來求解控制方程（1）、（2），具體步驟如下。

（1）忽略力源項，計算考慮初始壓力作用下的中間速度，即：

1.3 空間離散

2 驗證算例

如圖2 所示，計算域為一矩形區域，長×寬=15×10，流體次區域為邊長1.5的正方形，次區域左側距流場入口的距離為4.25，次區域中央浸沒一個剛性圓柱，其約束方式為全固定邊界，圓柱直徑為，圓心坐標為(0,0)。計算域左側為均勻來流入口邊界，采用Dirichlet 邊界條件，即=,=0；上、下兩側均為無穿透邊界；右側為自由出流邊界，采用Neumenn 邊界，即?/?=0，?/?=0 。整個流場采用一套間距為Δ=Δ=0.025的均勻四邊形網格，固體邊界采取與流體網格尺度相等的等間距離散，時間步長為Δ=0.002。

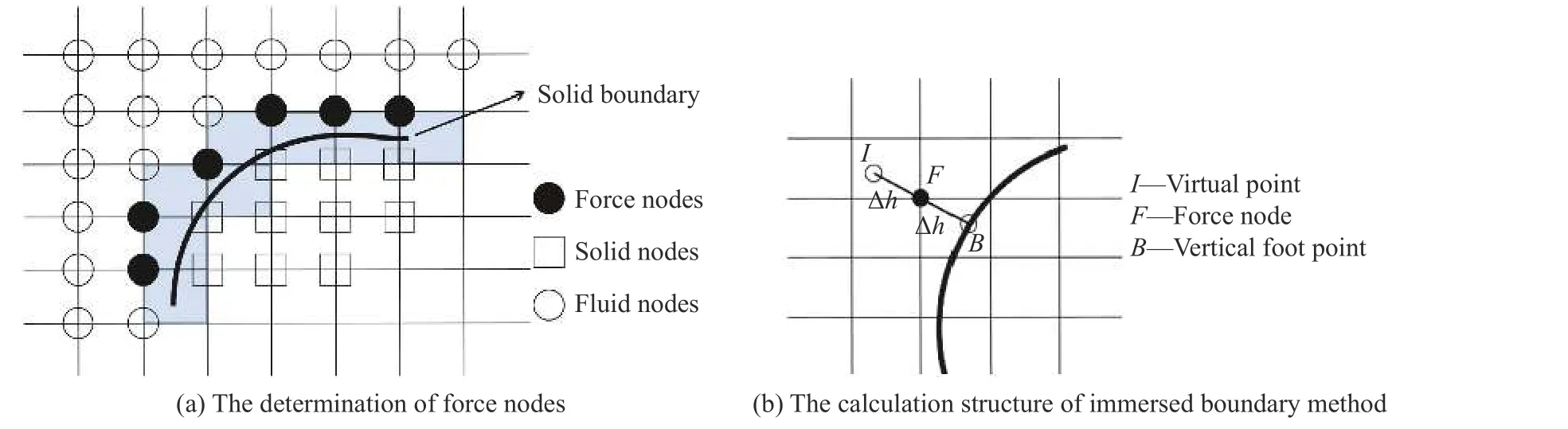
圖1 固體邊界處理Fig. 1 Treatment of the solid boundary

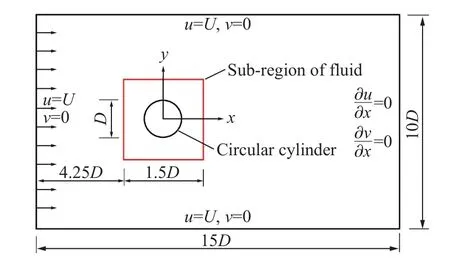
圖2 整體計算域及邊界條件Fig. 2 Computational domain and boundary conditions

圖3 為=160 s、雷諾數=300 時圓柱繞流的流場速度分布（范圍： - 1≤/≤1 ）。從圖中可看出，速度等值線表現光滑，說明計算過程中對速度的更新、修正并沒有造成流場的震蕩。由此可知，采用設置中間速度并不斷更新速度的方法是適用的。同時，固體邊界周圍的速度分布也符合真實的圓柱繞流流場分布規律。說明利用這種銳利界面法描述固體對流體的耦合作用和運用雙線性插值方法計算虛擬點的速度是可行的。

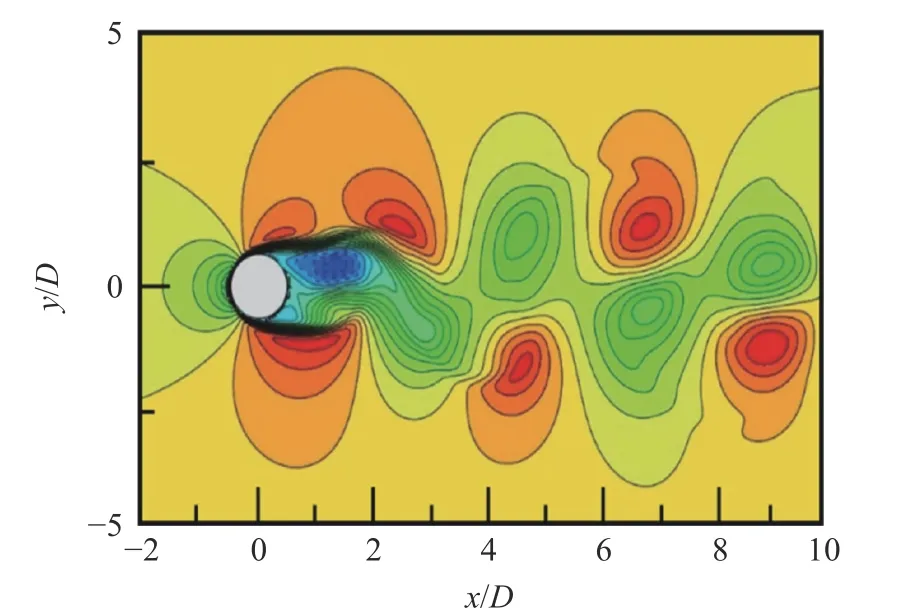
圖3 流向速度分布Fig. 3 Isolines of velocity

圖4 為一個渦脫落周期內圓柱尾跡渦隨時間的演化過程（范圍： - 8≤wD/≤8 ，為渦量；實線為正值，虛線為負值）。從中可看出柱體表面的邊界層分布、分離剪切層的卷起和圓柱后方的分離區域清晰可見。在一個周期內圓柱尾部出現明顯的正、負漩渦交替脫落，向下游發展，呈現出典型的卡門渦街現象，與試驗得到的卡門渦街現象一致。說明本文對邊界附近的流動參數插值的計算方法及程序是可行的。

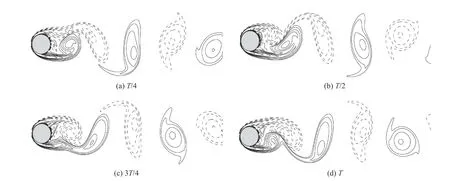
圖4 一個周期內尾跡渦的演化Fig. 4 Isolines of vorticity against time

圖5 為=300 時尾渦脫落穩定后的升力系數及阻力系數的時程曲線，可以看出，隨著時間的推進，流場逐漸趨于穩定，在流場穩定后升阻力系數都隨時間的發展而呈現出穩定的周期擺動。其阻力系數、Strouhal 數()的全時域統計結果見表1 所示。其中升力系數=2F/ρ，阻力系數=2F/ρ，Strouhal 數=/,為渦的脫落頻率。對比表中結果可知，相比于文獻[16,29]的數值解，本文的計算結果與文獻[30]的實驗值更為接近。驗證了本方法及程序的準確性。

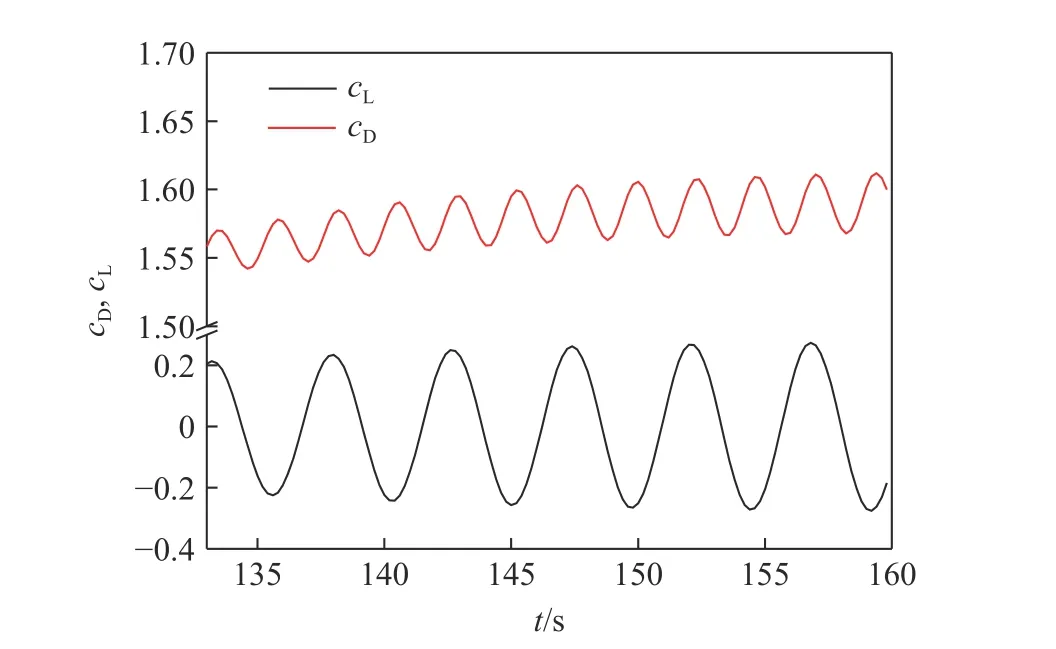
圖5 升力、阻力系數時程曲線Fig. 5 Variations of the lift and drag coefficients with time

表1 本文結果與其他文獻結果的對比（ R e=300 ）Table 1 The results comparison of average drag coefficients and Strouhal number at Re=300

3 橢圓柱主動運動算例

3.1 計算模型

目前，以圓柱為對象的鈍體繞流的研究已較為充分，對橢圓柱的關注度相對要少一些，但橢圓柱作為介于圓柱和平板之間更具有代表性的鈍體，其形狀更具流線型，流動阻力低，具有較好的對抗流體的作用，而且剪切邊界層的卷起、尾跡渦的脫落、轉捩和耗散等也很復雜，其研究對工程實際具有重要的現實意義。取計算域尺寸、邊界條件、網格尺寸、時間步長等均與驗證算例一致，雷諾數=800。不同之處在于：流體次區域中央浸沒的固體為一系列不同軸長比=/的橢圓柱（見圖6），其繞樞軸點（原點）旋轉擺動時攻角 θ （擺角）的變化規律由下式控制：

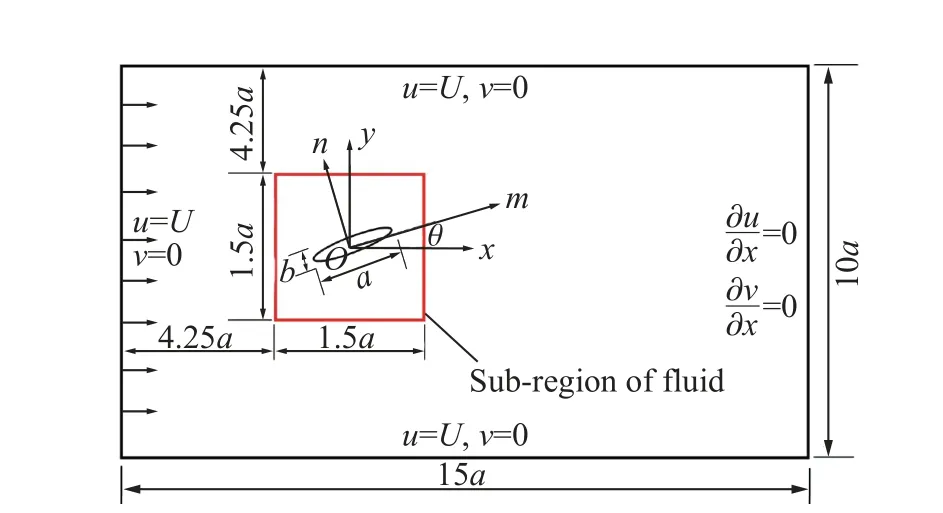
圖6 橢圓柱繞流計算模型Fig. 6 Computational model of flow around an elliptical cylinder

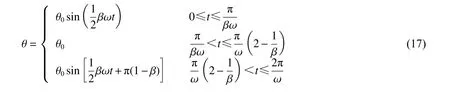
式中： θ為最大攻角值，取80°； ω =2π為振蕩角頻率，為運動頻率， β 為曲線形狀參數。該橢圓柱的擺動形式由水翼在正弦振蕩的基礎上演變而來（當 β=1 時為正弦波的半個波長）。 β=2.5 代表非正弦振蕩，前后0.2 s 為勻速開、關時間段，中間持續0.6 s，其1 個開、關周期內的方波曲線如圖7 所示。

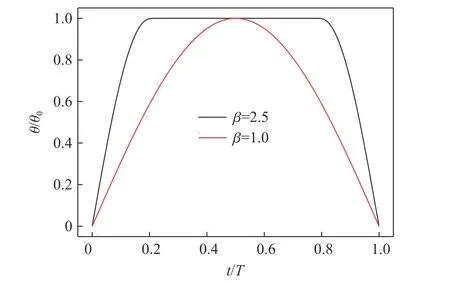
圖7 一個周期內橢圓柱的瞬時攻角變化曲線Fig. 7 Changes of the instantaneous angle of attack of the elliptical cylinder within a period

3.2 不同軸長比對橢圓柱繞流的影響

由圖8 可以看出，隨著的不斷增大，平均阻力系數以及最大升力系數 ||均逐漸增大。由于橢圓柱垂直于水流方向的投影面積不斷增大，當流體流過橢圓柱時，對橢圓柱的沖擊力增大，因此橢圓柱對流體的反作用力也會增大，橢圓柱所受到來自流體的阻力必然會增大。但是，相比阻力而言，升力的增大幅度比較小。由圖9 可以看出，渦脫頻率隨著軸長比的變化趨勢可以分成3 個階段。初期：隨著軸長比的增大而降低，當=0.2 時，橢圓柱的渦脫頻率最大，約為0.6 Hz；第二階段：當進入某一區域（=0.5～0.7）后，開始穩定下來，約為0.38 Hz；后期：當超出這一區間后，渦脫頻率將再次隨著的增大而遞減，“穩定現象”消失，在=0.9 時，達到最小值。

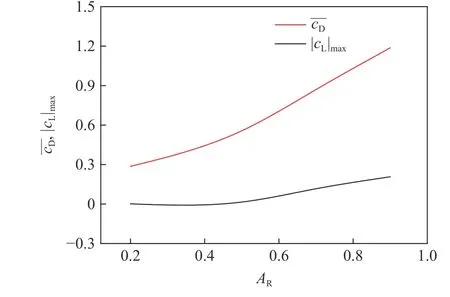
圖8 平均阻力系數、最大升力系數隨軸長比的變化Fig. 8 Variation of lift and drag coefficients with axis ratio

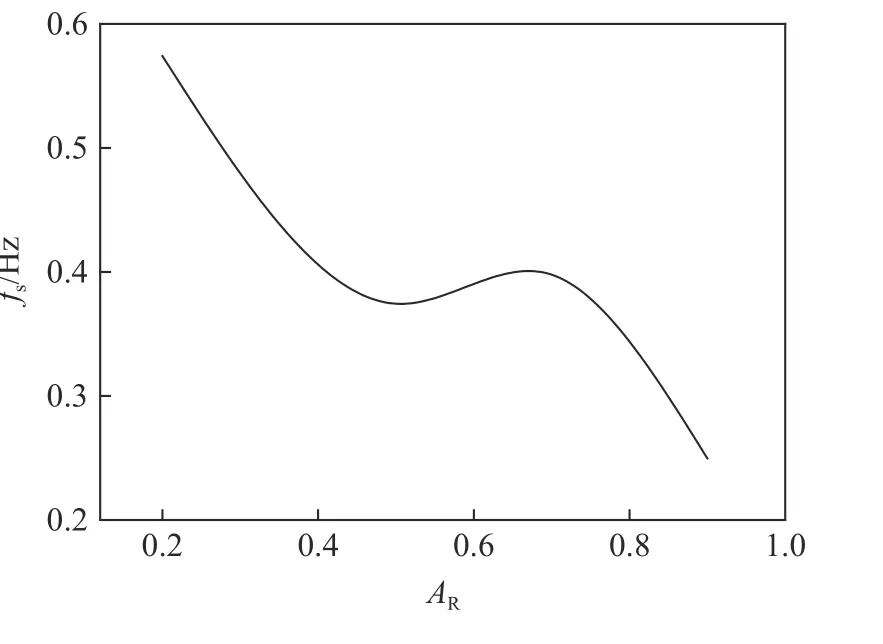
圖9 渦脫頻率隨軸長比的變化Fig. 9 Variation of vortex shedding frequency with axis ratio

由圖10 可知，當=0.2 時，橢圓柱更具流線型，流動阻力低，尾部并沒有明顯的分離渦，流場比較平穩；當=0.5 時，尾部流線波動開始逐漸明顯；隨著軸長比的增大，流態波動更加劇烈；當=0.7 時，在后方開始產生一個尺度較小的分離渦，其位置向上偏離橢圓柱的中心。

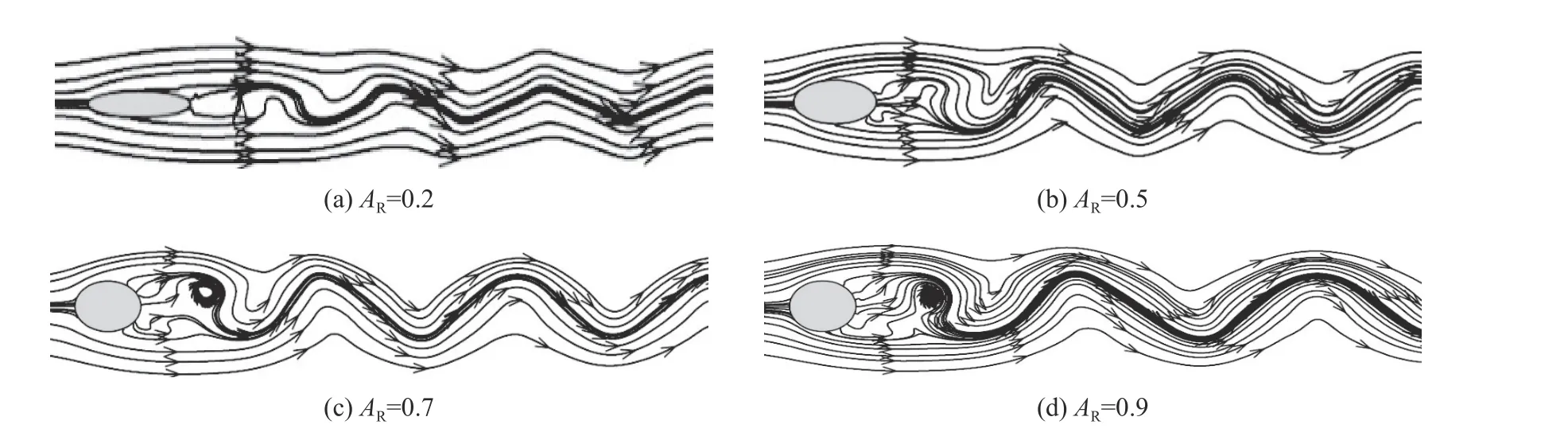
圖10 不同軸長比下的流線圖Fig. 10 The instantaneous streamlines with different axis ratio

圖11 為=800 時不同軸長比工況下，同一時刻下的瞬時渦量圖（ - 8≤wD/≤8 ，w為渦量；實線為正值，虛線為負值）。可以看出：當=0.2 時，尾跡渦以S 型模態脫落，呈現出上側負漩渦與下側正漩渦交替脫落向下游演化發展的卡門渦街現象。脫落的正負漩渦之間的縱向間距、周期較小，形成明顯的2 列，尾渦強度（尺寸）也較小，漩渦的分離點基本位于軸上；隨著軸長比的增大，卡門渦街規律依然明顯，但漩渦強度（尺寸）和周期逐漸增大，漩渦分離點偏離軸，且脫落位置增大，正、負漩渦中心間距減小逐漸趨于一列。

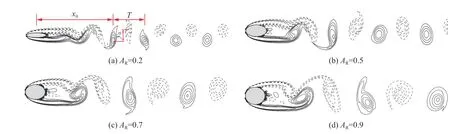
圖11 不同軸長比工況下的瞬時渦量Fig. 11 Variation of instantaneous vorticity with axis ratio

3.3 不同攻角對橢圓柱繞流的影響

圖12 給出了=0.2，=800 時，不同攻角 θ 下，升、阻力系數的變化規律。

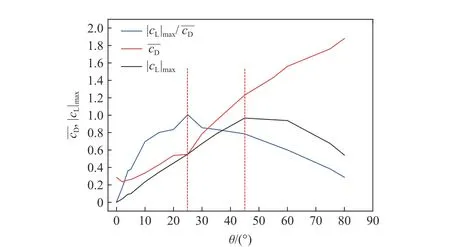
圖12 不同攻角對升、阻力系數的影響Fig. 12 Variations of lift and drag coefficients with angle of attack

從圖13 中也可看出，當 θ =0時橢圓柱上下表面的壓力對稱，壓差接近零，升力系數很小；隨著攻角增大，橢圓柱的上表面的壓力，不管從數值和承壓面積上來看都明顯比下表面大，即上下表面的壓差增大，故升力系數隨攻角的增大而增大。當攻角發展到臨界攻角 θ =45時，壓差達到最大，之后升力系數的值隨著攻角的增大而逐漸減小。

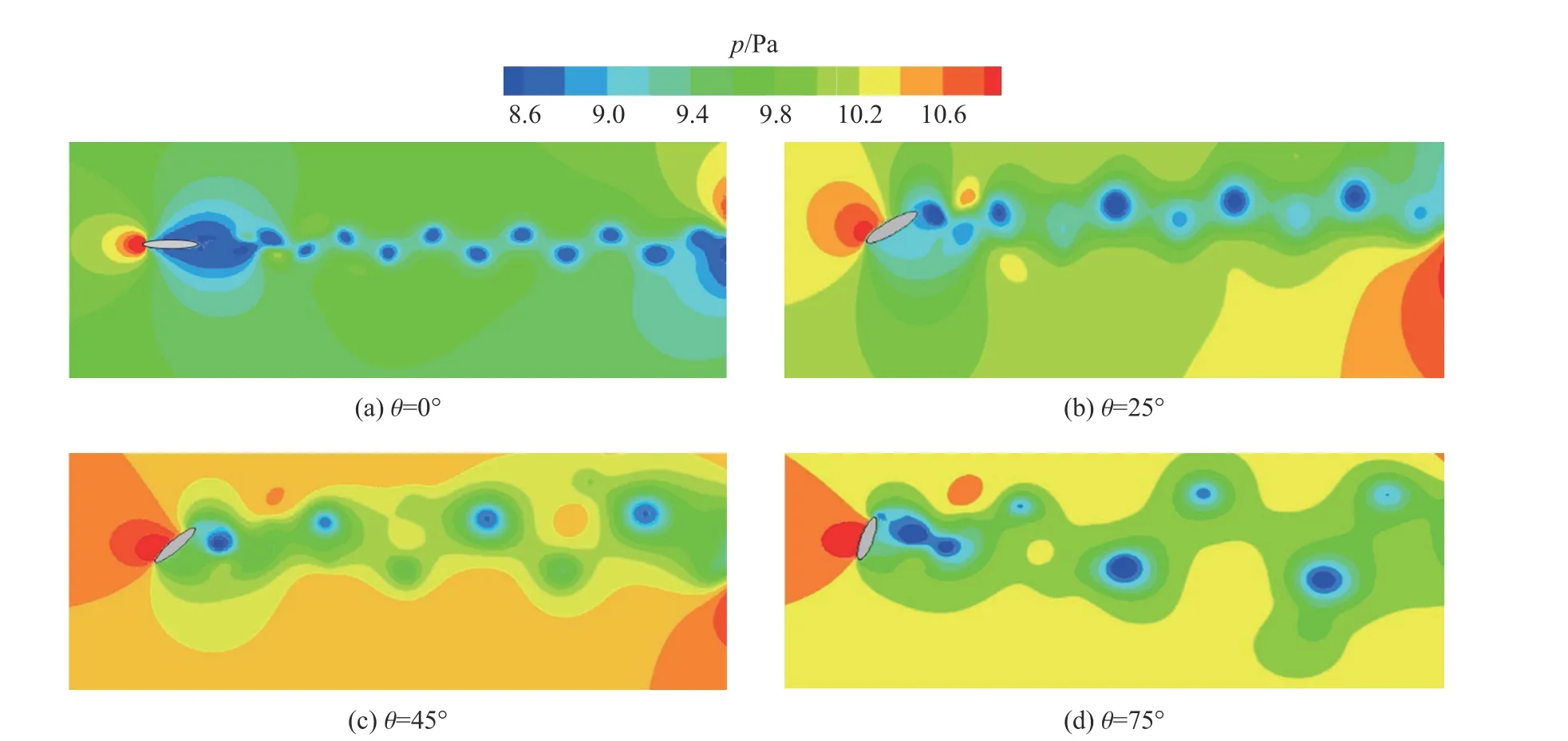
圖13 不同攻角下的瞬時壓力場Fig. 13 Instantaneous pressure fields at different angles of attack

由圖14 漩渦脫頻率曲線可以看到，渦脫頻率隨著攻角 θ 的不斷增大，整體呈現先增加再逐漸遞減的趨勢。其變化趨勢可以分成3 個階段：初期， θ =2°～5°階段，隨著攻角 θ 的增大而增加， θ =2時，渦脫頻率達到最大，約為=0.61 Hz；第二階段，當攻角進入 θ =2°～10°區域后，有所穩定，遞減速率較小，在0.6 Hz 左右浮動；后期，當攻角 θ ＞10后，渦脫頻率將隨著攻角 θ 增大而逐漸減小，后期曲線逐漸平緩，減小的速率逐漸減慢。

圖14 不同攻角對渦脫頻率的影響Fig. 14 Variation of vortex shedding frequency with angle of attack

圖15 為=800 時不同攻角工況下橢圓柱尾跡渦的對比，由圖可見，固體表面分布的邊界層、分離剪切層的卷起和橢圓柱后側的分離區，以及渦的脫落等現象都清晰可見。與圓柱繞流一樣，橢圓柱繞流尾跡渦也是呈現出明顯的一對正負漩渦從上下兩側交替脫落，向下游發展的卡門渦街現象。但是，橢圓柱擺動的攻角幅值對流態起決定性作用。隨著攻角的增加，渦的脫落周期、尺寸、形狀和演化形式等均有較大差異，渦脫落的反對稱性越發明顯。類似于水輪機活動導葉大攻角運行或導彈無側滑大攻角飛行時，背流（風）面分離渦的不對稱運動。攻角越大越容易產生不希望的附加偏航力，或加大水輪機活動導葉轉動軸折斷的風險。

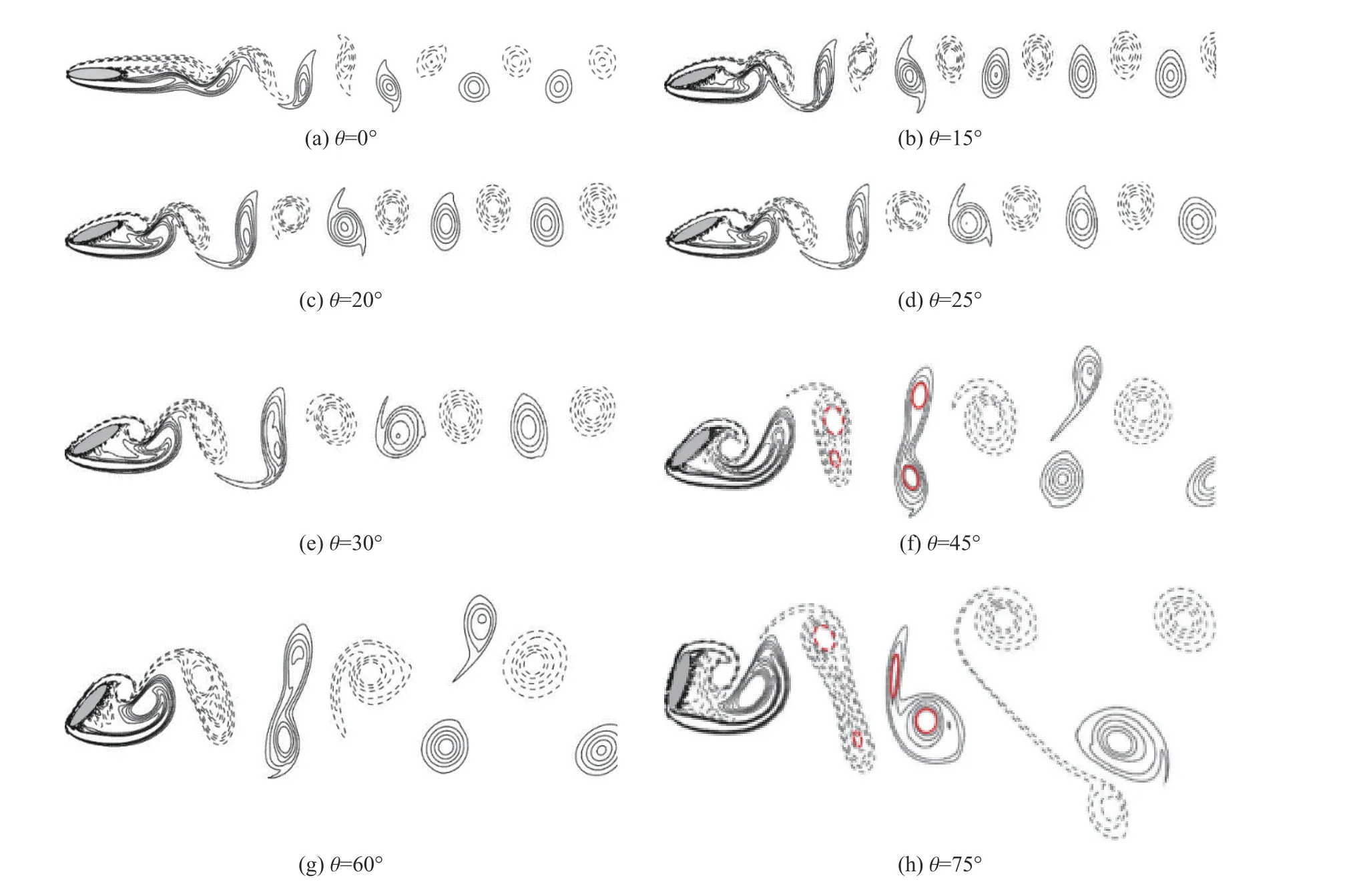
圖15 不同攻角下的瞬時渦量圖Fig. 15 Variation of the instantaneous vorticity with the angle of attack

隨著橢圓柱擺動攻角的增大，漩渦脫落頻率降低，周期加長，漩渦尺寸加大。當攻角 θ ≤30時，在每個周期內，有兩個符號相反的渦從橢圓柱上下側脫落，在下游形成交替出現的渦對，是典型的反對稱S 型脫落模態，如圖16(a)所示，類似于靜止圓柱的渦脫落方式。當 θ =45°～60°時，上下側脫落的漩渦尾部均拖著一個方向相同的子渦（2 個渦核）；在向下游演化發展的過程中，上側脫落的負漩渦的子渦與母渦融合，而下側脫落的正漩渦的子渦則產生分裂，分裂后的次正漩渦位于最上側，靠近負漩渦，最終尾跡渦表現為3 排，在下游形成了一對渦和一個單渦交替脫落的“P+S”Ⅰ型模態，如圖16(b) 所示。當θ≥75時，則情況相反，上側脫落的負漩渦的子渦發生分裂,分裂后的次負漩渦位于最下側，靠近正漩渦，而橢圓柱下側脫落的正漩渦的子渦則與母渦則融合，在下游形成了新的“P+S”Ⅱ型模態，如圖16(c)所示。

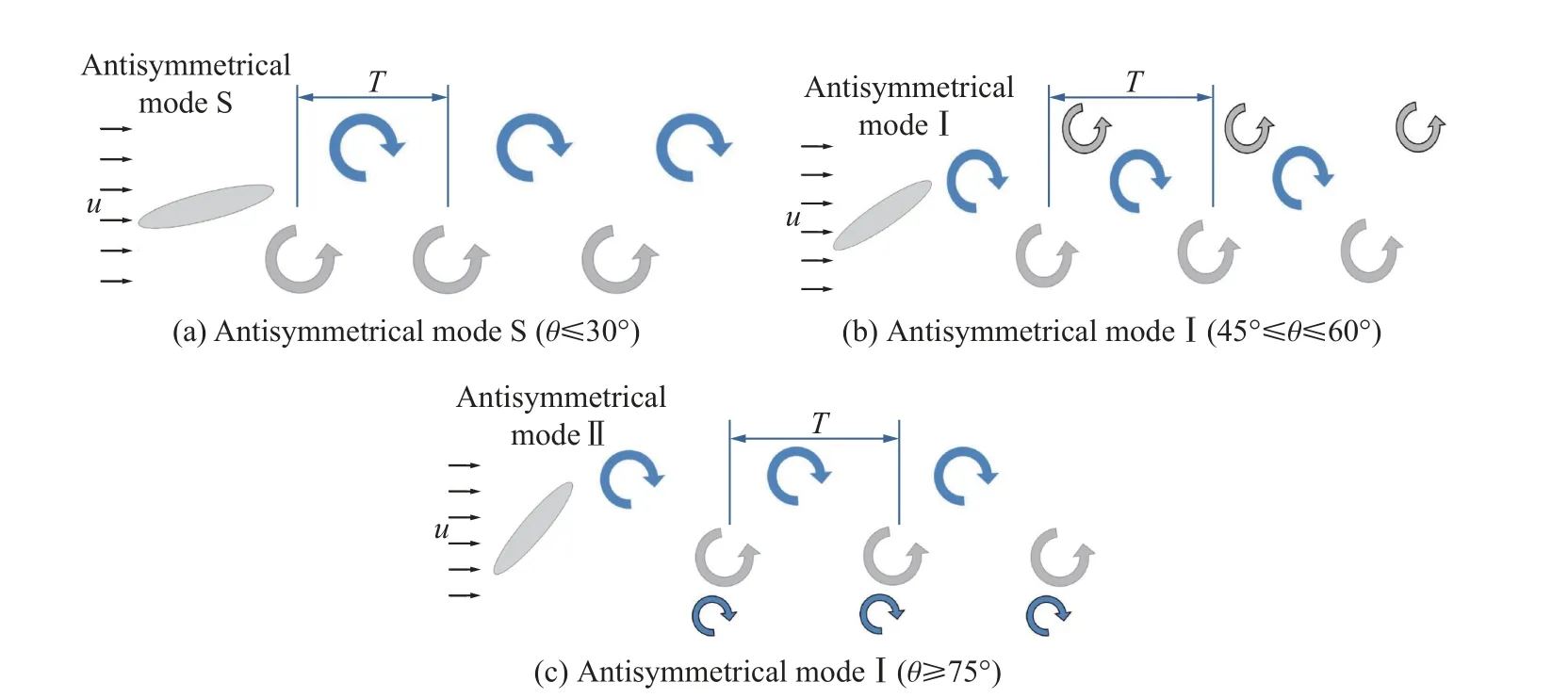
圖16 不同攻角下的渦脫落模態示意圖Fig. 16 The diagram of vortex modes at different angles of attack

4 結 論

采用一種銳利界面（sharp-interface）浸入邊界法對二維橢圓柱繞流問題進行了數值計算，并討論了不同軸長比、攻角 θ 對渦結構分布特征及升阻力系數、渦脫頻率等水力不穩定現象的影響，通過對比分析，得到以下結論：

(1)在模擬鈍體繞流時，通過與文獻和試驗結果的對比，本文的銳利界面浸入邊界法結果與試驗結果吻合較好，驗證了本方法的準確性和有效性；

(2)對于橢圓柱繞流問題，隨著不同軸長比的增加，升阻力系數呈遞增趨勢，而流場流態波動也越來越劇烈，尾跡渦脫落位置、強度（尺寸）、間距、周期也越來越大。周期加長，渦脫頻率則降低；

(3)當攻角發生變化時，平均阻力系數隨攻角的增大而呈遞增趨勢，而最大升力系數，以及最大升力系數和平均阻力比（升阻比），均表現為前期隨著攻角的增大而增大，超過臨界攻角后，再降低的趨勢；升阻比的臨界攻角為25°，而最大升力系數的臨界角為45°；

(4)當攻角發生變化時，渦脫頻率總體呈隨著攻角增大而逐漸減小的趨勢。漩渦脫落頻率降低，周期加長，漩渦尺寸加大；當攻角 θ ≤30時，尾渦呈反對稱S 型脫落模態，當 4 5≤θ≤60時，尾渦呈反對稱“P+S”Ⅰ型脫落模態，當 θ ≥75時，尾渦呈反對稱“P+S”Ⅱ型脫落模態。