基于深度展開的SAR大斜視RD成像算法

陳鷺偉， 羅 迎， 倪嘉成， 熊世超

(空軍工程大學信息與導航學院，西安，710077)

合成孔徑雷達(synthetic aperture radar，SAR)作為一種主動傳感器，可以對目標進行全天候、全天時、高分辨觀測，并且具備很強的穿透性，因此廣泛應用于軍事和民用領域[1]。斜視SAR由于具有靈活的波束指向，相比正側視SAR成像具備提前探測斜前視的能力，可以實現對敵方目標的實時偵察，因此研究大斜視角下的SAR成像算法具有重要的意義[2]。

斜視SAR由于波束指向與航跡不垂直，其回波信號具有大距離徙動特點，且存在距離向和方位向的嚴重耦合，常規的RD算法將斜距泰勒展開為低階形式，帶來了較大的誤差，在方位向上的聚焦性能具有局限性，因而不能適用于大斜視角的SAR成像。改進的RD算法雖然通過二次距離壓縮來提高成像質量，但在距離徙動校正、三次相位補償過程中引入了一定的相位誤差，成像質量隨著斜視角的增加下降[3]。Omega-K算法雖然可以對大斜視回波信號進行較為精確的成像，但需要大量的插值運算才可以完成[4]。

近幾年隨著深度學習的發展[5]，基于數據驅動的智能學習方法已成功運用到SAR圖像解譯當中，這些方法從海量的SAR圖像數據中學習得到“圖像域”到“目標參數域”的非線性復雜映射[6-7]。該類方法的優點是普適性強，能夠最大程度地擬合數據間的復雜映射關系，但是存在著神經網絡拓撲結構設計難度大、網絡參數多等問題。針對這些問題，文獻[8]提出一種將算法簇深度展開為網絡的方法，將乘子交替方向法(alternating direction method of multipliers, ADMM)展開成網絡形式，獲得了比傳統 ADMM 算法更加精確的結果。文獻[9]采用軟閾值迭代算法(iterative shrinkage-thresholding algorithm，ISTA)設計深層展開網絡，并應用于稀疏信號重構中，相比傳統ISTA算法大幅提升了信號重構精度。文獻[10]初步驗證了深度學習方法SAR成像中的可行性，但所提方法的可學習參數少，對迭代算法的依賴性較強。

綜上所述，目前雖然已有一些文獻研究基于深度學習的SAR成像技術，但是這些工作的成像模式一般設定在正側視條件下，還未有針對在大斜視條件下的SAR學習成像技術研究。因此，本文提出了一種基于深度展開網絡的大斜視可學習距離多普勒(LRD)成像算法,兼顧SAR成像時間以及成像精度，同時也能夠改變RD對于斜視角度的限制。

1 大斜視SAR回波信號模型分析

SAR大斜視成像系統與觀測場景之間的位置關系如圖1(a)所示，其中，平臺的高度為h，斜視角為θ0，假設平臺作勻速直線運動，速度為Vr，R0為航線與觀測場景中心的最近距離，RB(t,τ;R0)為平臺與點目標之間的瞬時斜距，其中t為快時間變量，τ為慢時間變量。

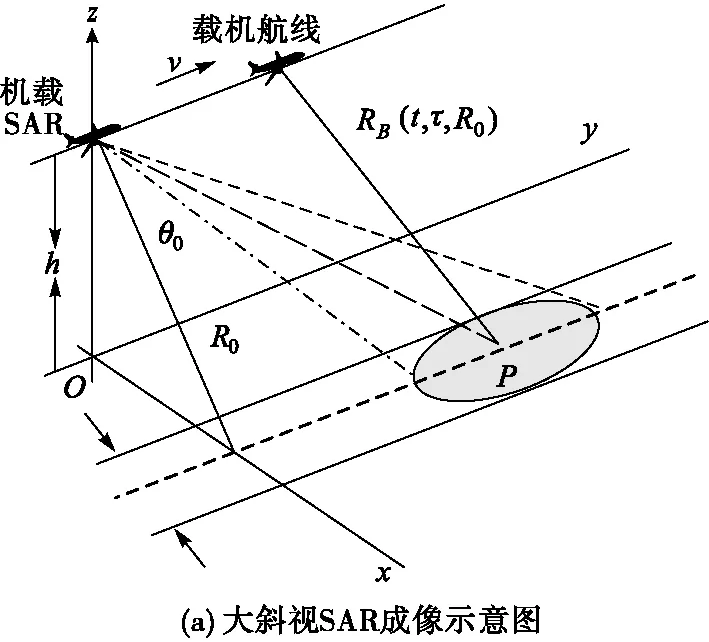
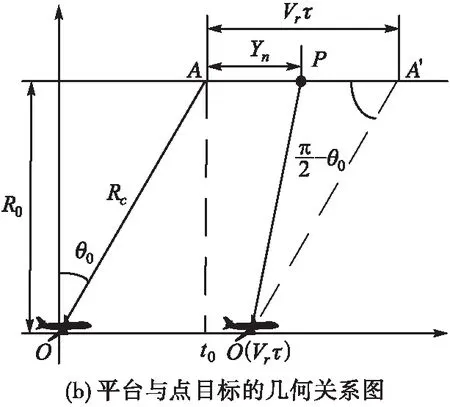
圖1 大斜視SAR成像模型示意圖

圖1(b)為SAR平臺與點目標的幾何關系，設O點為慢時間的起點，則A點同樣也是慢時間的起點，t0為波束中心穿越時刻，Rc為A點到平臺的距離，則根據余弦定理可以得到平臺與點目標P之間的瞬時斜距為：

RB(τ;Rc)=

(1)

假設雷達發射線性調頻信號(linear frequency modulation，LFM)，調頻率為Kr，脈沖寬度為Tp，則平臺接收到的基帶回波信號為：

(2)

式中：ξ為雷達工作波長，wa、wr分別為方位向、距離向的包絡。

傳統的RD成像算法是將公式(1)進行二階近似，忽略高階項帶來的誤差，直接在距離多普勒域進行距離徙動校正，經過距離壓縮和方位壓縮成像。算法未考慮大斜視回波信號的特點，因此不符合大斜視角條件下的成像要求。

下面將RB(τ;Rc)進行泰勒級數展開得到：

RB(τ;Rc)=Rc-(Vrτ-Ynsinθ0+

(3)

從式(3)可以看出，線性項為距離走動項，高次項為距離彎曲項，當斜視角足夠大時，高次項的值很小，因此可以忽略距離彎曲對包絡的影響。結合式(2)、(3)可以看出距離彎曲項和雷達波長處于同一個數量級，因此不可以忽略距離彎曲對回波相位的影響。

下面將回波信號變換到距離頻域上，忽略兩個維度的信號包絡，對其進行距離走動校正和距離向脈沖壓縮。

走動誤差為:

ΔRw=Vrτsinθ0

(4)

構造的匹配濾波函數為:

(5)

式中：fr為距離向頻域；f0為雷達工作頻率。此時，經過走動校正、距離壓縮后的回波信號，多普勒中心的頻率搬移到零頻，因此雷達發射波束的中心線位于零多普勒平面。經過以上操作得到的回波信號為：

(6)

其中:

(7)

(8)

經過壓縮后的信號，距離向和方位向的耦合程度大大降低，但仍存在著殘余距離徙動以及距離彎曲項對相位的影響。改進的RD算法在二維頻域上分別構造二次距離壓縮、三次相位補償函數以及方位向脈沖壓縮函數解決上述問題，具體構造方法可參考文獻[3]，本文不再贅述。改進的RD算法在構造上述壓縮函數和補償函數時均采用了不同程度的近似，當斜視角增大時，其成像精度和質量逐漸下降。

2 大斜視SAR LRD成像網絡

2.1 成像網絡構建

針對第1節大斜視SAR成像存在的問題，本文通過深度學習的方法，將二次距離壓縮、三次相位補償函數H2和方位脈沖壓縮函數H3作為可學習的參數，通過網絡學習得到相比傳統算法更加精確的成像矩陣，從而提高成像精度、改善聚焦效果。為了更好地描述可學習參數與成像結果的關系，結合式(2)、(5)以及文獻[3]將大斜視SAR的RD成像算法過程寫成矩陣相乘的算子形式：

(9)

(10)

式中：*表示矩陣共軛操作。根據式(9)、(10)的分析，SAR成像可以看作為一個線性求解的逆問題，該二維觀測模型可以通過求解最優化問題得到:

(11)

其中λ‖Θ‖p為正則化約束項，λ為正則化系數。式(11)的求解依靠迭代優化算法(如ISTA、AMP)實現，這些傳統算法要求其中的矩陣M-1是精確已知的，并且在迭代過程中，迭代參數的選擇需要通過人工進行多次調試才能獲得較好的解，這無疑提高了計算復雜度和時間成本。

本文所構建的LRD成像網絡是建立在式(9)的大斜視SAR二維觀測模型的基礎上，將式(11)的求解算法深度展開成網絡形式。需要注意的是，由于網絡中成像矩陣H2、H3是可學習的矩陣，式(11)的求解在成像網絡中不再是一個線性問題，而是一個復雜的非線性求解問題，因此需要在網絡中添加非線性變換實現回波信號到SAR圖像的非線性擬合。以ISTA算法求解式(11)為例，ISTA算法主要分為殘差計算、算子更新以及軟閾值迭代3個步驟，因此在深度展開網絡中，同樣在網絡的第k層(k=1,2,…,K)構建相應的3個子網絡層，具體描述為：

1)殘差層：用R表示，該子網絡層用來計算殘差，在成像網絡的第k層中，通過第k-1層輸出的場景散射系數計算關于大斜視回波信號的殘差，具體的表達式為

(12)

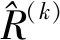
2)算子更新層：用P表示，該子網絡層的輸入為殘差層計算得到的殘差，并作用于M，具體表達式為：

(13)

(14)

式中：β為迭代步長，在傳統ISTA中每一次迭代中，β的值是固定的，而在成像網絡中是一個可學習的參數。

3)非線性變換層：用F表示，該子網絡層用來體現成像網絡的非線性映射能力，通過對算子更新層得到的進行非線性變換，獲取大斜視SAR回波信號到場景散射系數的非線性映射能力，同時輸出下一層的場景散射系數。具體表達式為:

(15)

F(P(k);λ,T)=soft(P(k);λ,T)=

sign(P(k))(|P(k)|-T)

(16)

式中：F(·)為成像網絡的非線性變換；soft(P(k);λ,T)表示與正則化參數λ有關的軟閾值函數；sign(·)通常為符號函數，在所構建的成像網絡中，將其直接作為非線性變換層的激活函數，T為迭代閾值。該網絡層可學習的參數可以為迭代閾值T，正則化參數λ。

綜上所述，所構建的大斜視SAR LRD成像網絡的單層拓撲結構由殘差層、算子更新層、非線性變換層3個子網絡層構成，并且可學習的參數集為Ω={H2,H3,β,T,λ}。需要說明的是，在網絡訓練過程中為了減小網絡學習參數的規模，成像矩陣H2、H3僅在一輪反向傳播訓練后發生變化，迭代參數β、Τ、λ在每一層中則是可變的。圖2和圖3分別給出了所構建網絡的整體網絡拓撲結構以及單層拓撲結構。其中單層的拓撲結構由迭代算法中一次迭代過程決定，整個大斜視SAR LRD成像網絡包含具有相同的拓撲結構的k層。

圖2 大斜視SAR LRD成像網絡結構示意圖

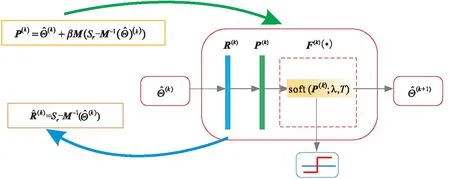
圖3 第k層網絡結構示意圖

2.2 網絡數據生成與訓練

一般來說，雷達觀測場景是未知的，無法直接對回波樣本中添加有關場景散射系數的標簽數據；另一方面，由于網絡性能受到監督訓練的標記訓練樣本的限制，如果采用監督的訓練方法，并根據常規的大斜視SAR成像結果進行標記，則該網絡的性能受到常規成像方法的限制。因此，本文采用非監督的訓練方式對成像網絡進行訓練。

回波樣本生成方面，由于樣本生成是訓練和測試前的預處理，是可以離線完成的，因此樣本生成的準確性比時間開銷和計算負擔更重要，同時，由于完全準確的真實散射信息難以獲得，實際測量數據很難建立有效的樣本集，為了得到較為精確的回波樣本集，本文采用理想的隨機點散射模型并根據式(2)的回波信號模型生成大斜視SAR回波，并加入系統環境噪聲，在不改變SAR成像模型的情況下生成大量回波數據樣本。設定回波樣本數量為N，回波樣本集Sn={S1,S2,…,SN}，其中n=1,2,…,N為回波樣本序列號。

在回波樣本集構建完畢之后，通過設計損失函數實現非監督學習，對網絡進行誤差反向傳播時，因為采用的是非監督學習，無法直接度量網絡的輸出與真實場景散射系數之間的差異，而是直接利用網絡最后一層得到的場景散射系數估計值作用于M-1，得到SAR回波的估計值并與真實回波進行對比。其回波估計值表達式如式(17)所示，設定損失函數為均方誤差函數(mean square error，MSE)，具體如式(18)所示:

(17)

(18)

在網絡訓練過程中，可學習參數集Ω的訓練實質上是在求解優化損失函數的最小化。這可以通過許多現有深度學習優化器來實現，包括梯度下降、時間反向傳播等。需要注意的是，由于大斜視SAR回波是復數據，但在成像網絡中數據均為實數傳播，因此，所構建的網絡可以采用基于隨機梯度下降的Adam優化器進行訓練。同時為了防止在訓練成像網絡過程時出現梯度消失情況，將學習率設定為較小的值，在滿足條件的同時，收斂的速度盡量快。

3 仿真實驗與分析

本節將采集得到的大斜視SAR回波數據作為樣本，并仿真在噪聲環境下對成像性能的影響，對仿真數據進行成像驗證。同時為了驗證所提算法的優越性，將其與改進后的RD算法以及傳統ISTA算法進行比較，需要注意的是，在與ISTA比較時，我們將ISTA的迭代次數設置為與所提成像網絡的網絡層數相等。

3.1 點目標仿真實驗

首先對噪聲環境下的點目標成像性能進行驗證。成像模式為條帶模式，觀測場景內包含有3個目標散射點。

在生成訓練樣本和測試樣本方面，通過加入隨機加性高斯白噪聲產生1 000個回波樣本，信噪比的范圍為-15～30 dB，并且隨機選取樣本數量的70%作為訓練樣本，30%作為測試樣本。

在訓練階段，對于網絡參數的初始化，根據文獻[3]將成像矩陣H2和H3初始化，進一步得到Θ0，對迭代參數初始化λ0=0.8,β0=0.8，T0=0.5，得到初始化參數集Ω0。設定學習率為η=0.001、batch size設置為4，整個樣本集的訓練次數(epoch)設置為1 000，訓練樣本Ntrain= 700。

在測試階段，測試樣本為Ntest=300，對測試樣本集取平均得到最終的成像結果。最終成像時，將網絡學習得到的成像矩陣H2及H3、迭代步長、正則化參數、迭代閾值作為固定值輸入成像網絡，成像過程就轉化成一次網絡的前饋運算，可以直接輸出成像結果。表1給出仿真對應的雷達參數以及網絡參數。

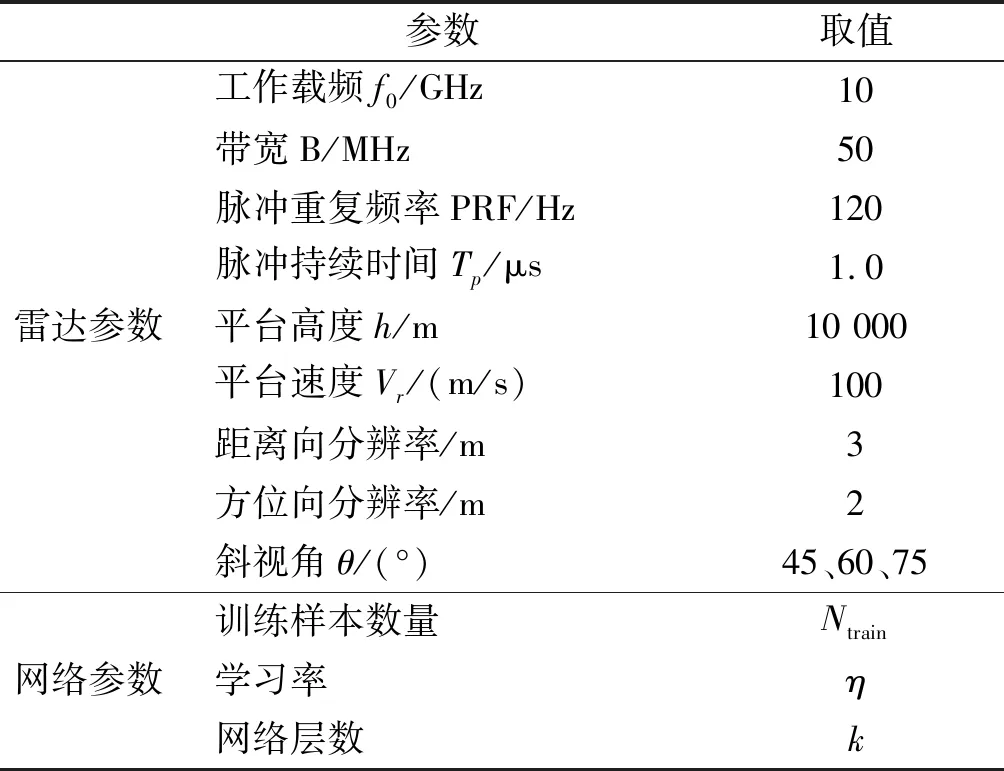
表1 雷達參數和網絡參數

本文所提方法采用Python、Tensorflow1.14實現成像網絡模型，所有實驗均在一臺個人電腦(Intel i7-10875H，16GB RAM)上完成，并且利用一塊英偉達Geforce RTX 2060顯卡進行GPU加速。圖4給出不同網絡層數下訓練集的損失函數曲線圖，可以看出，網絡在訓練到50次左右時開始收斂，誤差逐漸趨于0，隨著網絡層數的增加，網絡的收斂速度變慢，誤差的振蕩幅度在前50次訓練逐漸變大。為了平衡網絡的誤差以及網絡大小之間的關系，本文的仿真實驗均設置網絡層數為8層。

圖4 不同網絡層數的誤差曲線圖

設定雷達工作在X波段(0.03 m)，點目標在距離向和方位向均相距30 m，場景中心點與載機航跡的最近距離為10 km，圖5給出在信噪比15 dB條件下，不同算法的點目標成像結果對比圖。需要注意的是，大斜視條件下，成像之后點目標的位置在距離向和方位向上均存在著偏移，因此需要進行幾何校正。圖5是經過幾何校正之后的結果，本文采取的幾何校正方法為文獻[11]，這里不再贅述。由圖5可以看出，3種算法均能夠對點目標進行正確成像，改進的RD成像算法點目標周圍旁瓣較高，且當目標相距不遠時，容易在旁瓣交叉處形成虛假目標；L2范數ISTA雖能夠有效抑制旁瓣，但需要手工調試參數才可以滿足成像要求，而本文方法可以將學習到的參數輸入成像網絡直接成像，實現點目標的精確聚焦，體現出良好的成像性能。同時，本文方法在斜視角較大的情況下仍可以有效適用。

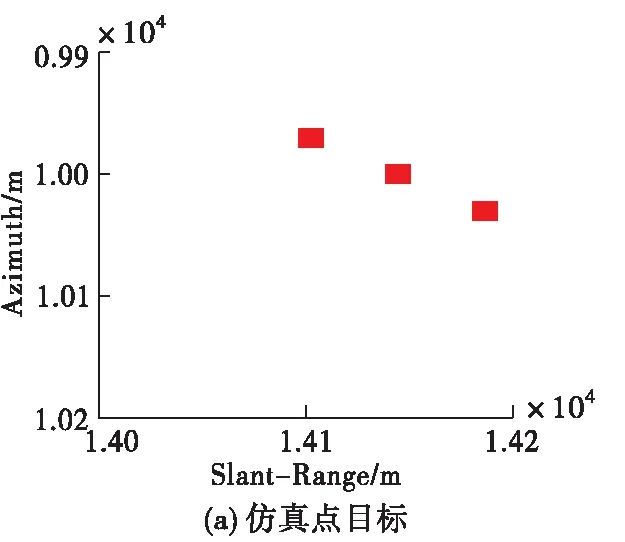
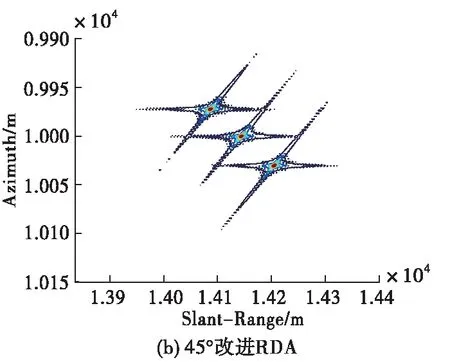
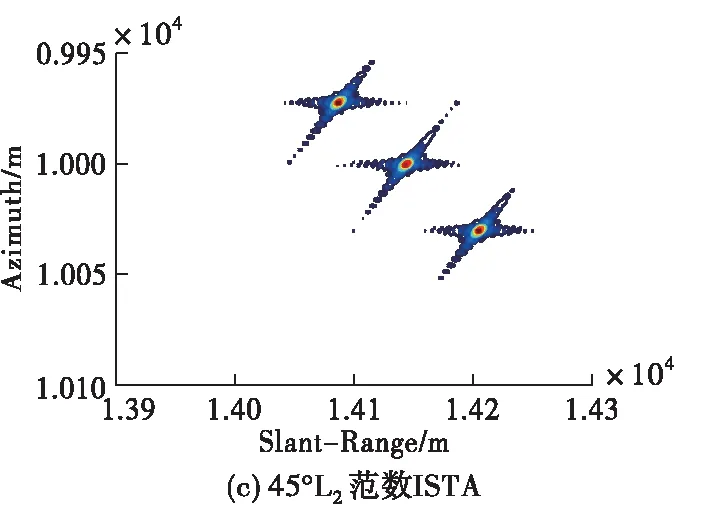
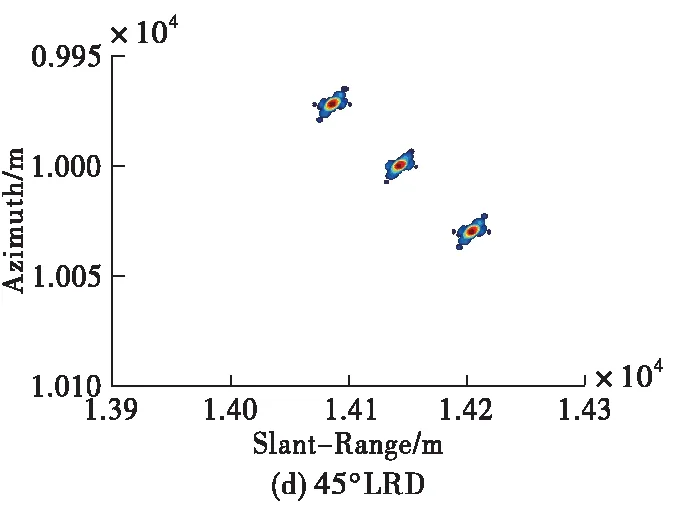
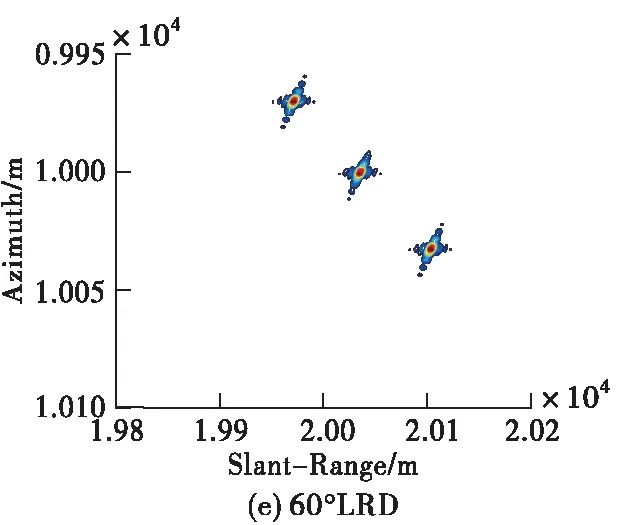
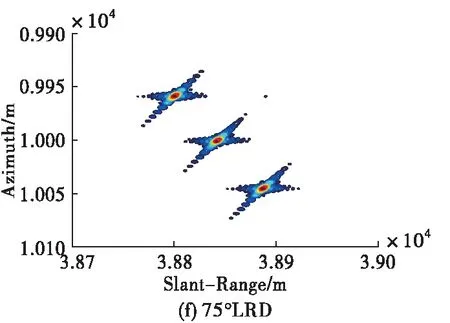
圖5 15 dB信噪比條件下點目標成像結果對比

3.2 算法對比分析

為了展示所提成像方法的優勢，現將所提方法與傳統大斜視成像算法(如Omega-K、NCS)做對比，需要說明的是，由于其它成像算法均為采取插值操作，為了方便與其它算法進行對比我們對點目標仿真時采用的是無須Stolt插值的近似Omega-K算法[12]，仿真條件設置為15 dB信噪比、斜視角為45 °條件下，其余參數均與表1相同。對比結果如圖6所示。從圖中可以看出，本文方法抑制旁瓣的效果相比于Omega-K算法、NCS算法更好，展示了較好的成像性能。

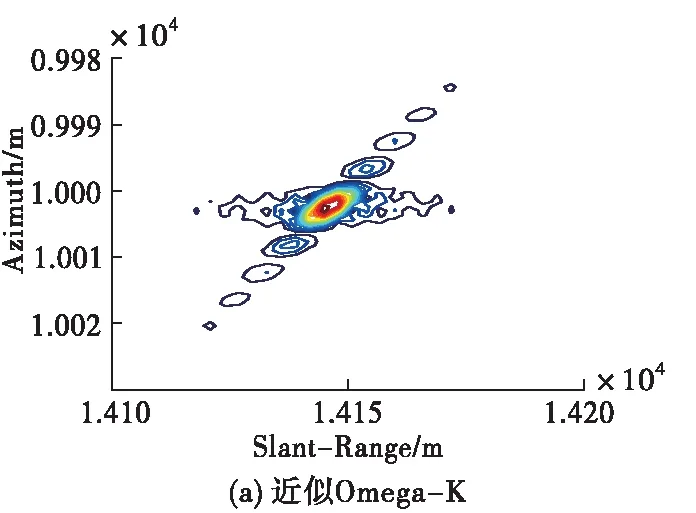
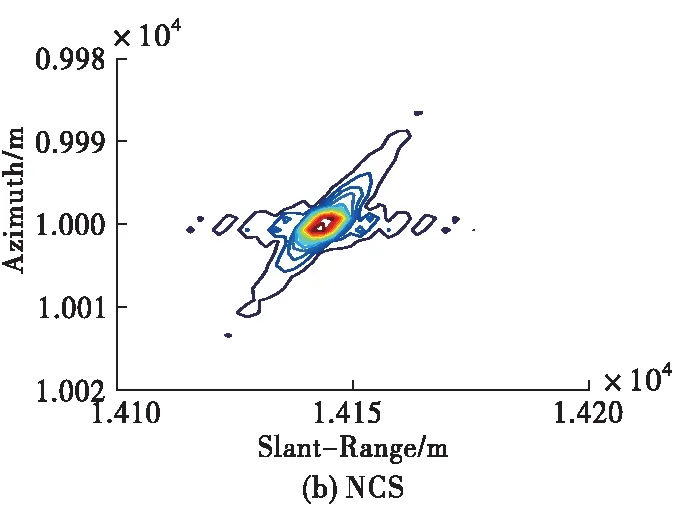
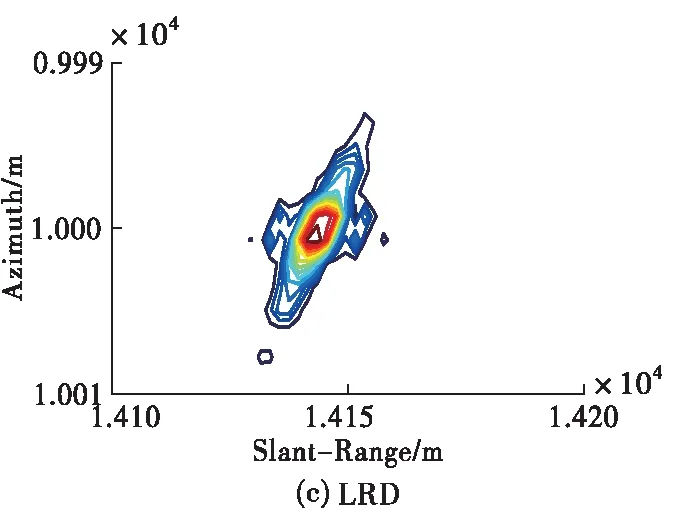
圖6 不同算法的點目標仿真結果

由于所提方法在經過網絡深層迭代之后，其所有參數均已固定，此時當輸入大斜視SAR回波時，網絡相當于進行一次前饋運算即可得到SAR成像結果。因此在計算其運算量時[12]，實際上僅需計算式(9)中所涉及的操作即可，其包括距離向FFT、方位向FFT、復數相乘、距離走動校正、2次距離壓縮和3次相位補償等。假設估算浮點運算量(FLOP)的參數分別為：輸入距離線數Nri=4 096，每一輸入距離線上的采樣點數Nrg=4 096，每一輸出距離線上的采樣點數為Nro=3 072。

因此所提方法中涉及到的距離向FFT的浮點運算量GFLOP = 5NriNrglog2(Nrg)/109≈ 1.01，方位向FFT的GFLOP=5NroNrilog2(Nri)/109≈ 0.76；復數相乘的GFLOP=6NriNrg/109≈ 0.10；2次距離壓縮及3次相位補償的GFLOP=12NriNro/109≈ 0.16。從而計算出所提方法總的運算量為4.48GFLOP，在回波數據大小相同的條件下，近似Omega-K算法總運算量為3.95GFLOP，NCS算法總運算量為6.34GFLOP，L2范數ISTA算法的運算量為48.26GFLOP。

同時為了定量對比所提方法與傳統成像算法的成像性能，分別采用峰值旁瓣比(peak side lobe ratio，PSLR)，積分旁瓣比(integral side lobe ratio，ISLR)來進行衡量，需要說明的是，這些指標均為場景中心點目標經過計算得到。為了比較成像時間，對所有算法均成像50次取平均值，其結果如表2所示，所提方法在PSLR、ISLR等指標較傳統算法有明顯提高，并且所提方法的成像速度與傳統算法處以同一數量級，而較ISTA算法成像速度快。綜合來看，所提方法相比傳統成像算法能夠同時兼顧成像效率以及成像精度。

表2 45°斜視角、15 dB信噪比條件下不同算法成像質量評價指標結果對比

3.3 面目標仿真實驗

為了進一步說明本文方法的有效性，下面對面目標進行仿真驗證。其中面目標的仿真涉及到的雷達參數以及網絡參數設置與點目標仿真實驗一致，回波信號同樣加入系統環境噪聲。場景的大小為100 m×100 m，網絡輸入回波矩陣S的大小為300×484，實驗仍與RDA、L2范數ISTA等傳統算法作對比，圖7給出了仿真實驗結果對比圖。從圖可以看出，改進RD成像算法在面目標成像時旁瓣較高，并且還存在著距離/方位的交叉耦合，傳統ISTA雖能有效抑制旁瓣，但是算法迭代成本較高。而所提的方法既可以有效完成距離/方位的解耦、抑制旁瓣，對于一些重點目標也能夠精確成像，得到較為理想的成像結果。

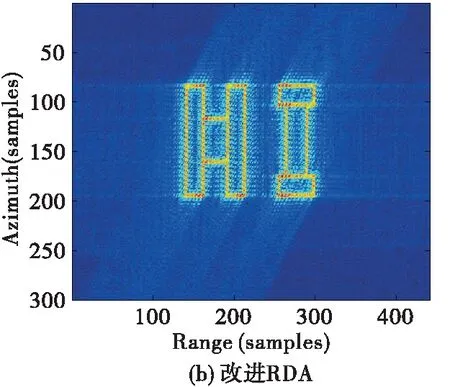
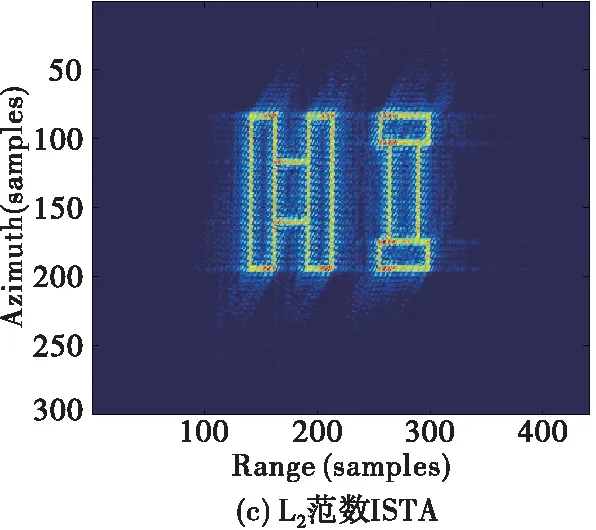
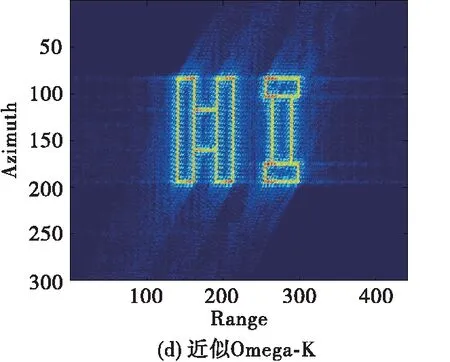
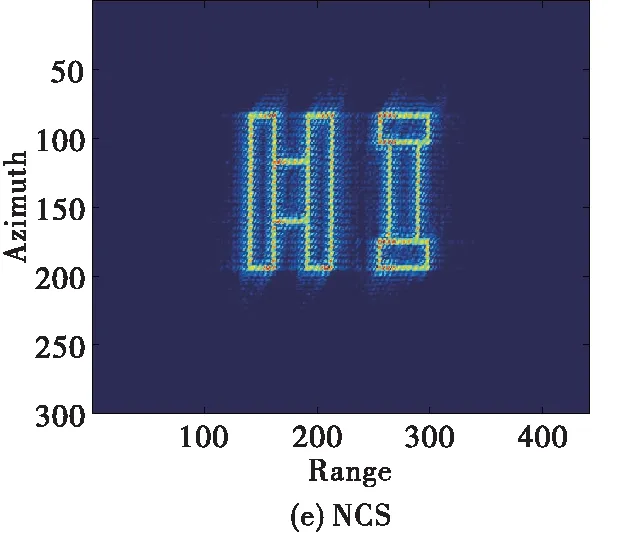
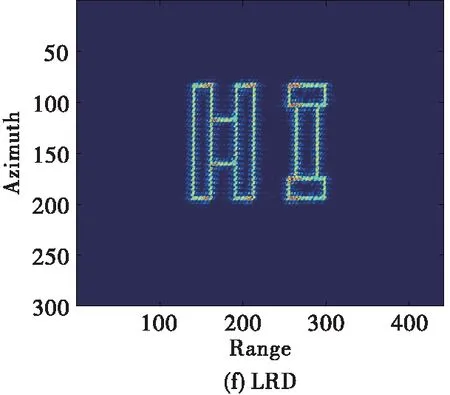
圖7 45°斜視角、15 dB 信噪比條件下仿真面目標成像結果對比

4 結語

針對大斜視SAR的回波信號具有嚴重的距離/方位耦合，大距離徙動等特點，本文首先對大斜視SAR回波信號進行分析，而后確定成像網絡所需學習的參數，建立大斜視SAR二維成像網絡模型，然后通過學習訓練得到較為精確的成像矩陣以及迭代參數；最后，將回波數據、學習到的參數直接輸入到成像網絡中，輸出質量較好的SAR圖像。通過具體的點目標和面目標的仿真實例，對本文所提方法的正確性和有效性進行了分析和驗證。仿真結果表明，所提方法對于提升大斜視角下的SAR成像性能具有良好的效果，成像精度相比于改進的RD算法、傳統大斜視成像算法也有了進一步的提高，滿足大斜視條件下的成像要求。