基于卡爾曼濾波的UWB與里程計融合定位方法

黃俊杰，李海濱，賈翠玲

(1.內蒙古工業大學材料科學與工程學院，內蒙古呼和浩特 010051；2.內蒙古工業大學工程訓練教學部，內蒙古呼和浩特 010051)

0 前言

隨著物聯網技術的快速發展，工廠、商店、醫院等都在走向智能化，人們對定位的穩定性和精度的要求變得越來越高。在室外環境中，依靠全球衛星導航系統(Global Navigation Satellite System，GNSS)如GPS、北斗等與慣性導航系統(Inertial Navigation System，INS)的組合導航可以達到很高的定位精度，但是由于GNSS信號容易受復雜環境影響，在室內無法提供有效的定位數據，因此開發可靠的室內定位系統(Indoor Positioning System，IPS)具有很高的實用價值。

超寬帶(Ultra-Wideband，UWB)是利用極窄脈沖傳輸低功率無線信號的新興通信技術，時間分辨率高，定位精度可以達到厘米級別，在穿透性、抗多徑能力和抗干擾性方面都有著很好的表現，加上高的傳輸功率和低功耗的特點，所以UWB廣泛應用于室內高精度定位。但是同其他無線定位系統一樣,數據抖動和非視距環境下的數據失真也是UWB系統存在的主要問題。從動輪式里程計固定在機器人上，結合陀螺儀的角度信息可以對機器人的位置信息進行實時計算，具有結構簡單、成本低、短時精度高等優點。從動輪式里程計在短時內有很好的定位效果，但是隨著時間增長會產生較大的累計誤差，所以單一的里程計模式不適合長時間定位。文獻[9]提出了一種結合馬爾可夫鏈和指紋匹配算法的UWB技術，是一種解決NLOS(Non-Line of Sight)誤差問題的有效方法，但是需要先對UWB的數據在指紋數據庫中進行匹配，計算量過大。文獻[10]提出了一種基于UWB、里程計和RGB-D融合的室內定位方法，使用了加權平均的思想，成功將誤差抑制在10 cm以內，但并沒有對UWB處于嚴重非視距狀態下的情況進行處理。文獻[11]提出了一種基于改進自適應加權數據融合的粒子濾波定位算法，與擴展卡爾曼融合算法相比其定位精度提高了15%以上。文獻[12]通過求解LiDAR(Light Detection and Ranging)定位信息與粒子之間的幾何距離來更新粒子的權重,從而彌補UWB的非視距誤差。但是這2種方法都沒有對嚴重非視距狀態進行判斷，而且沒有對IMU(Inertial Measurement Unit)和LiDAR的累計誤差進行判斷和消除，導致系統長時間運行效果不好。

針對上述問題，本文作者提出一種基于卡爾曼濾波的UWB和里程計數據融合的定位方法。該方法將里程計短時精度高和UWB長時誤差有界性的優點進行融合，有望在單片機上實現長時高精度定位。作者先以里程計的數據作為參考量對UWB數據進行非視距情況的判斷；然后使用卡爾曼濾波算法對里程計和UWB數據進行不同信賴度下的融合；再使用融合后的數據對里程計數據進行累計誤差的判斷和修正，來減小里程計的累計誤差，提高系統長時間運行的精度和穩定性，以實現長時高精度定位。

1 傳感器原理及誤差產生原因

1.1 超寬帶定位

1.1.1 定位算法原理

UWB基站和標簽使用雙向飛行時間法(Two Way-Time of Flight, TW-TOF)可以得到基站和標簽之間的距離，如圖1所示。

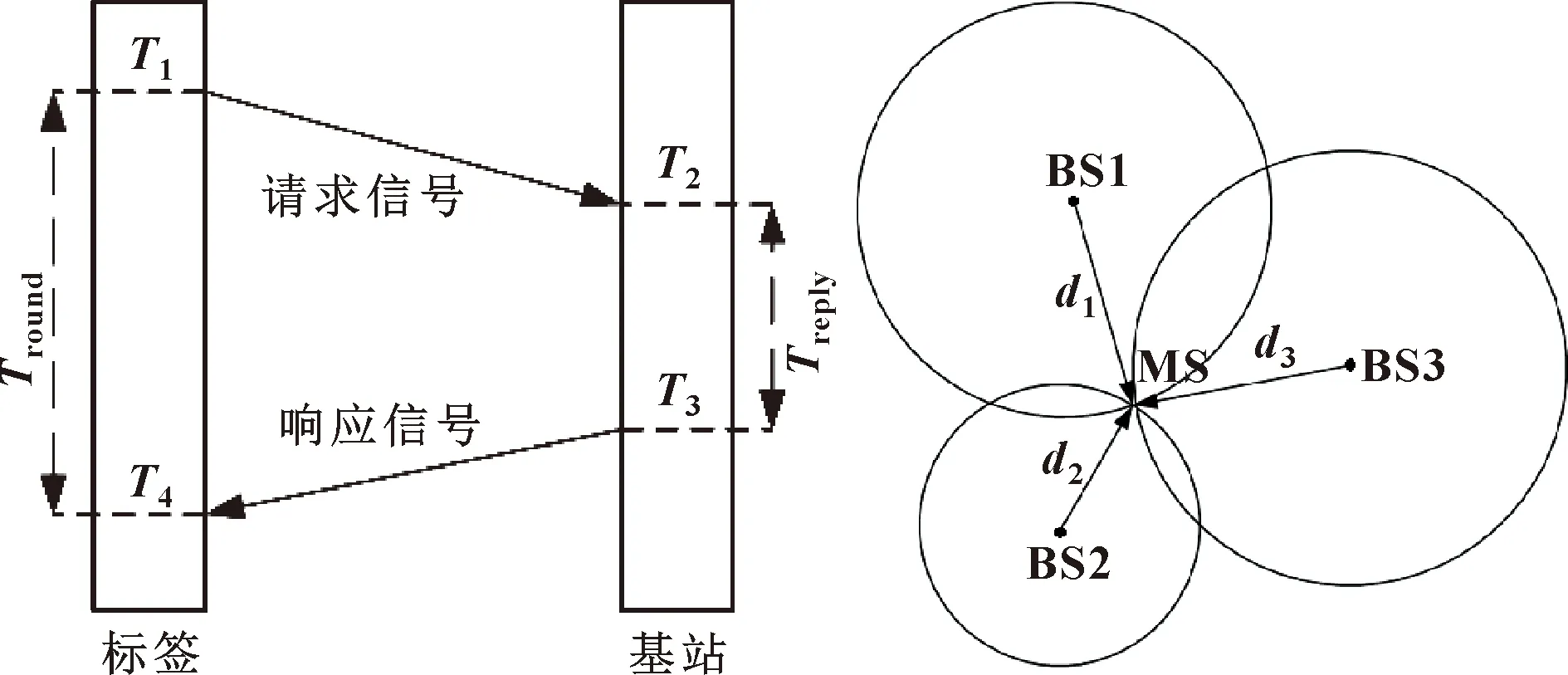
圖1 TW-TOF測距方法 圖2 三邊定位算法原理

標簽在時刻發射請求性質的脈沖信號，基站在時刻接收到信號，在時刻發射一個響應性質的脈沖信號，標簽在時刻接收到，由此可以計算出信號總飛行時間和處理時間。無線電傳播速度為光速，則可以得到兩模塊的距離。

(1)

在超寬帶定位過程中，采用三基站一標簽的定位方法，使用三邊定位算法得到標簽的坐標信息，如圖2所示。

假設標簽的坐標是(,)，第個基站的坐標是(,)，基站到標簽的距離是，此時二維模型下標簽坐標滿足式(2)：

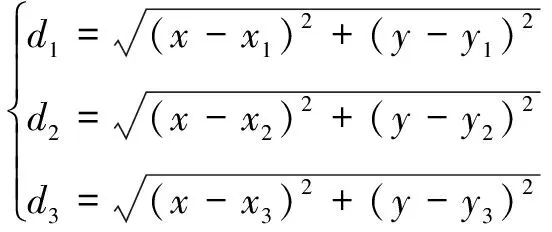
(2)

將式(2)各公式進行平方后得到一個非線性方程組，用方程組中的前-1個方程減去第個方程，整理后得到線性方程組=

其中：

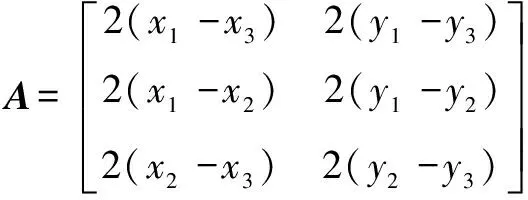
(3)

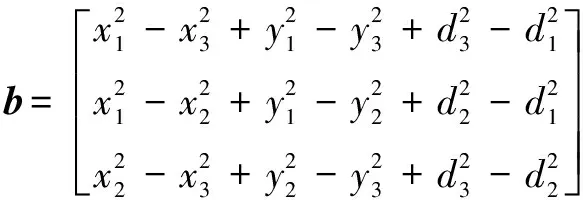
(4)

使用最小二乘法求解方程可以得到標簽坐標：

=()

(5)

1.1.2 非視距誤差產生原因

當UWB信號傳播遭到障礙物的阻擋而無法直線傳輸時，就會出現UWB定位的非視距問題。在非視距傳播情況下，信號只能穿透障礙物或者借助反射、折射和衍射的方式進行傳輸，使得到的信息含有大量失真信號，嚴重影響三邊定位算法的計算精度。

1.2 輪式里程計定位

輪式里程計定位系統由圖3所示的正交從動輪式里程計和一個JY61六軸陀螺儀組成，輪式里程計由2個正交的全向輪和2個光電編碼器組成，由陀螺儀來提供姿態角。

圖3 正交從動輪式里程計

將里程計固定到移動機器人底盤上，里程計的2個全向輪相對于移動機器人車體中心的垂直距離分別為和。計算單個采樣周期內機器人的位移坐標增量，然后積分，從而得到機器人相對于參考坐標系的位姿狀態。如圖4所示，在一個采樣周期內，2個光電編碼器測得2個全向輪旋轉軌跡的增量為d和d。機器人相對于機器人車體坐標系的位移增量分別記為d和d,可以由d和d以及機器人旋轉角與、等參數表示。機器人相對于參考坐標系的位移增量分別記為d和d，可由d和d及機器人旋轉角表示。機器人的旋轉角度為可由JY61六軸陀螺儀給出。

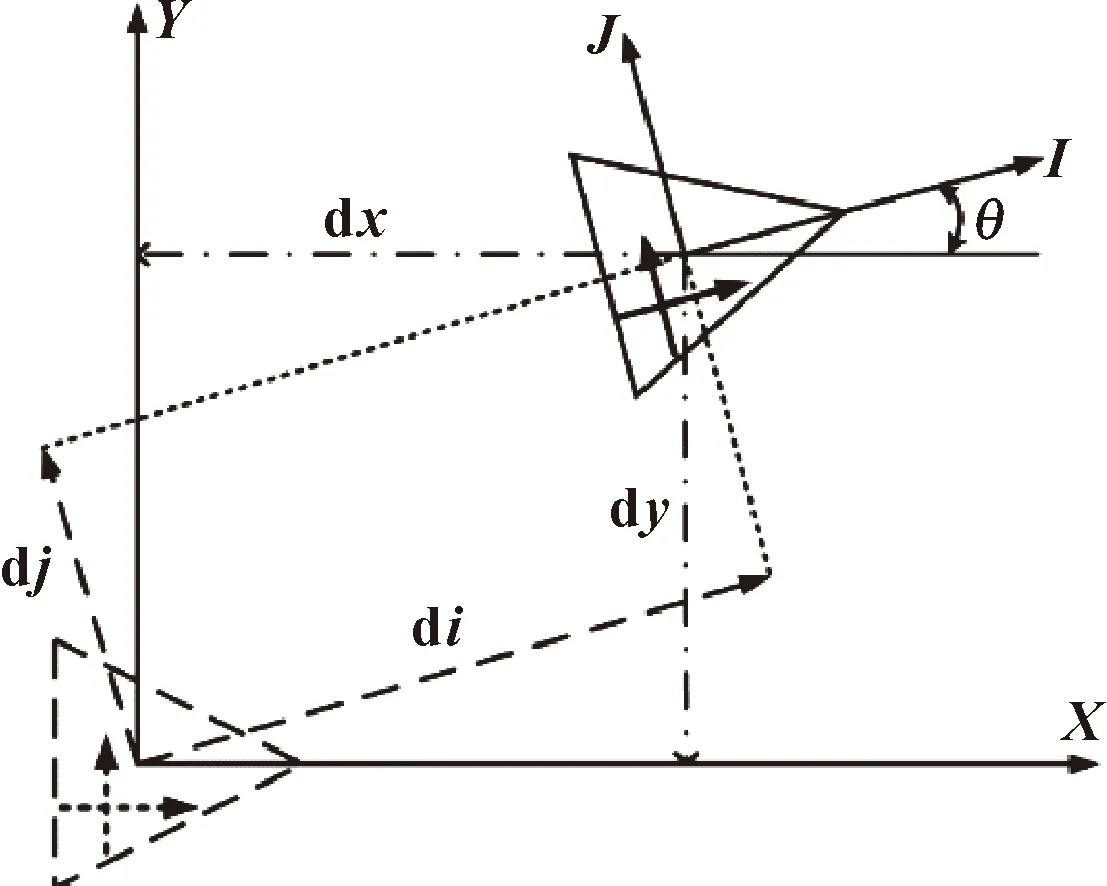
圖4 機器人移動姿態

最后將d和d進行積分，得到機器人相對于參考坐標系的位姿信息(,,)。

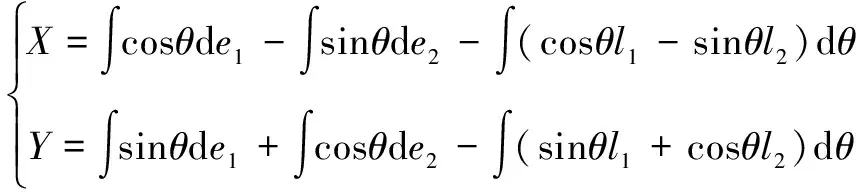
(6)

輪式里程計的數據具有信號頻率高、短時精度高的特點，但是如果不經過校核，容易產生較大的累計誤差。

2 基于卡爾曼濾波的數據融合定位系統

輪式里程計配合JY61六軸陀螺儀通過公式(6)可以得到機器人位姿信息，短時精度高，但是長時會有較大的累計誤差，數據可信度降低。UWB可以得到一個沒有累計誤差的坐標信息，視距情況下可維持10 cm左右的定位精度，但在非視距環境下會出現數據失真導致數據可信度降低。基于里程計短時精度高和UWB長時誤差的有界性，將2種信息進行有機融合以達到長時高精度定位的目的。首先用輪式里程計所得數據作為參考量，對UWB進行狀態判斷，判斷UWB是否處于視距環境中；再使用卡爾曼濾波算法對里程計和UWB進行不同信賴度下的融合；然后使用融合得到的數據對里程計數據進行累計誤差的判斷與修正，從而降低里程計的累計誤差,提高系統定位精度。數據融合的計算流程如圖5所示。

圖5 數據融合的計算流程

2.1 判斷UWB狀態

先對UWB數據進行一次一階低通濾波，以初步減小數據的抖動，然后分兩層對UWB數據狀態進行判斷。

第一層先對UWB的單點數據進行判斷，需要獲知UWB基站是否得到標簽的距離信息，因為在定位中可能出現障礙物引起基站無法得到標簽信息的情況，使三邊定位算法不能正常使用，導致UWB數據失效。通過第一層的判斷可以排除無法得到單點數據的情況，如能得到單點數據則進入第二層判斷。

在第二層中對UWB數據做是否進入非視距狀態與非視距程度的判斷。用當前的UWB數據對里程計的數據求距離偏差，在里程計的數據上設定多層環形區域，通過判斷UWB所屬區域對非視距程度進行分類量化，為后續數據融合提供依據。將UWB所處狀態分為3類，則有式(7)所示分類量化結果。

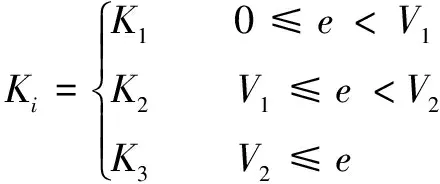
(7)

式中：為第類視距狀態,其中=(1,2,3)；表示狀態閾值；為距離偏差值。表示UWB處于視距狀態，因為文中實驗使用的UWB系統的定位精度為10 cm，所以取值可在15 cm左右，但是不能小于UWB本身的定位精度。表示UWB處于輕度非視距狀態，這個非視距狀態的數據尚可以使用，具有一定的可信度，表示允許使用的非視距狀態誤差距離的最大值。表示UWB已經處于嚴重的非視距狀態，數據已經完全不可信。經過上述兩層判斷，實現了以里程計為參考量的UWB非視距程度的分類量化。

在上述工作基礎上，將對里程計數據和分類量化后的UWB數據進行數據融合。

2.2 基于卡爾曼濾波算法的數據融合

卡爾曼濾波的數學模型包括預測模型和觀測模型2個部分,離散化的形式如式(8):

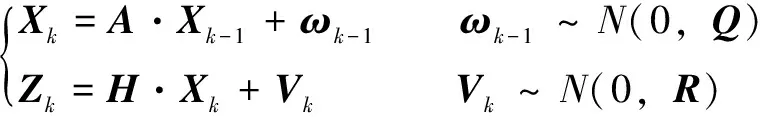
(8)

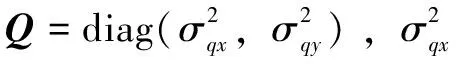
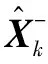
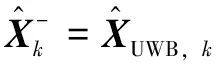
(9)

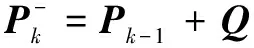
(10)

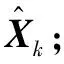
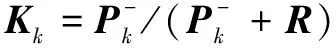
(11)

(12)

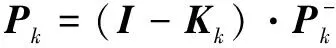
(13)

在上述卡爾曼濾波算法公式中已省略對單位矩陣的書寫。

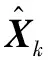
用式(7)分類量化的結果設置參數，表示UWB數據處于視距狀態，則和可以設置為相同的值，即設里程計和UWB值具有相同的可信度，這對參數使用、表示。表示UWB處于輕度非視距狀態，則通過增大、減少來提高系統對里程計的信賴度，這對參數用、來表示。表示UWB處于嚴重非視距狀態，UWB數據失去作用，此時系統以里程計數據為準，設置為單位矩陣，設置為零矩陣，此時=、=。綜上所述，將UWB的視距狀態與和的參數取值歸納為式(14)。

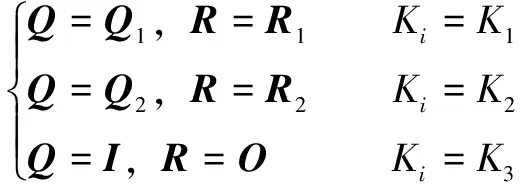
(14)

在UWB處于不同狀態下使用式(14)改變預測值噪聲的協方差和觀測值噪聲的協方差，從而改變融合系統對觀測和預測的信賴程度，進而達到自適應的效果，提高了系統的穩定性。

2.3 里程計累計誤差的判斷和修正

使用融合后的數據來判斷里程計的累計誤差。以得到的融合后的數據為圓心設定一個圓形許用區域，通過判斷里程計數據所在區域對里程計累計誤差進行判斷。如果里程計的數據連續多次超出圓形許用區域，則表明里程計已經產生了較大的累計誤差。設定的圓形許用區域半徑越大則對里程計的累計誤差的容忍度越大，圓形許用區域半徑越小則對里程計的修正會越靈敏。但實驗使用的UWB的定位精度為10 cm，視距情況下的數據融合對里程計和UWB信賴度相同，融合后的數據在兩者之間，所以圓形許用區域的最小半徑不能小于5 cm。

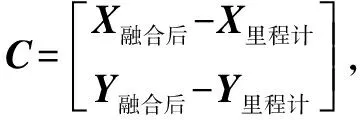
(Corrected)=(orignal)+

(15)

再用修正的里程計的數據參與數據融合，從而提高系統長時定位的精度。

3 仿真與實驗驗證與分析

3.1 仿真實驗

仿真實驗使用開源機器人仿真軟件Webots，仿真機器人由全向運動底盤、輪式里程計和UWB定位系統組成。其中全向運動底盤和輪式里程計通過在Webots中直接建模生成，UWB定位系統使用軟件中的GPS傳感器通過設定傳感器的噪聲來模擬產生不同狀態的UWB信號。仿真機器人模擬完成如圖6所示的蛇形運動，先向軸正方向運動3 m，然后向軸正方向運動1 m，向軸負向運動3 m，軸正向運動1 m，如此反復，得到的數據如圖6—圖7所示。

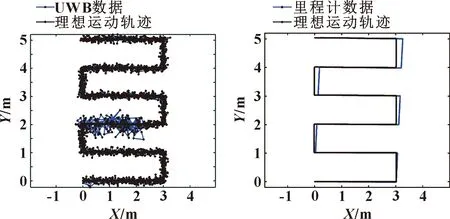
圖6 理想軌跡與UWB數據形成的軌跡 圖7 理想軌跡與里程計數據形成的軌跡

圖6為UWB數據的軌跡圖，可以看出：機器人從(0，2)到(2，2)的運動期間設定UWB為非視距狀態，具體表現為UWB數據抖動幅度變大。圖7為里程計數據的軌跡，里程計在運行過程中產生了累計誤差，隨著時間的增加誤差也在增加。

圖8為最終融合得到的數據，系統成功判斷出UWB的狀態，并進行了不同信賴度的融合，得到穩定的數據。并且在(3.057,2.625)m點處融合后的數據判斷出里程計的累計誤差，并對里程計數據進行了修正。然后使用修正過的里程計數據繼續與UWB進行融合，減小了融合后數據的累計誤差，提高了系統長時間運行的穩定性。

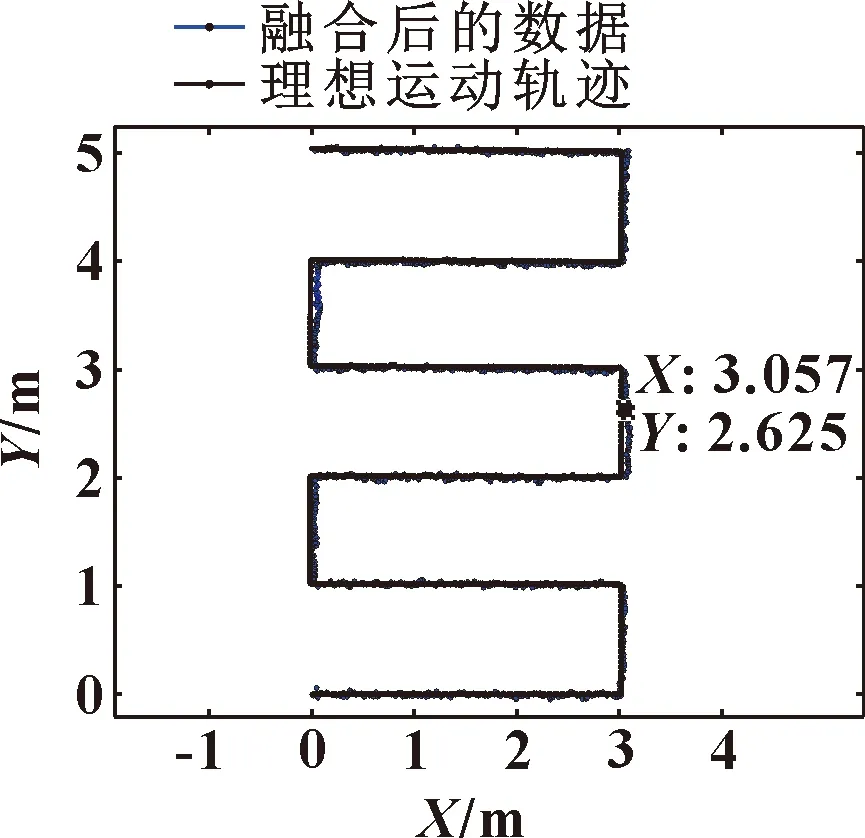
圖8 理想軌跡與最終融合后數據的軌跡

圖9為每個UWB原始數據與理想位置坐標的誤差和每個融合后數據與理想位置坐標的誤差對比，可以看出：融合后的數據相對于UWB原始數據的抖動和誤差都明顯減小，而且在非視距情況融合后的數據依然有很好的穩定性和準確性。融合后的數據誤差會隨著時間的增加逐漸變大，這是由于里程計的累計誤差逐漸增大所致，但當里程計的累計誤差達到一定程度時，又會通過融合后的數據對里程計數據進行修正，從而將里程計數據的累計誤差控制在一定范圍之內。UWB原始數據的平均誤差為0.101 5 m，融合后的平均誤差為0.048 3 m，融合后的數據誤差減少了52.41%，達到了良好的預期效果。

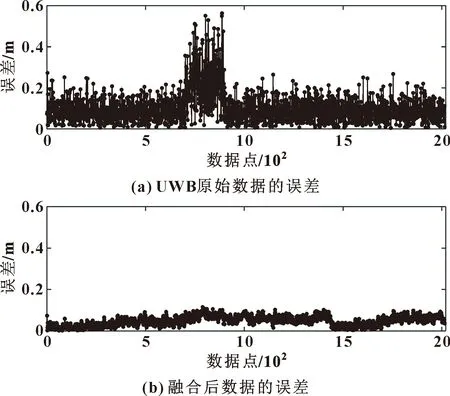
圖9 UWB原始數據的誤差和融合后數據的誤差對比

3.2 實驗驗證與分析

為進一步驗證文中方法在單片機系統中的應用效果，擬開展實物機器人定位實驗研究。實驗采用基于Decawave公司的DW1000芯片的UWB產品，該產品定位范圍為50 m，組成的系統定位誤差為10 cm左右。采用的輪式里程計為自制的正交從動式輪式里程計如圖3所示，平均運行10 m會產生5 cm的累計誤差。JY61六軸陀螺儀采用TDK公司的MPU6050姿態傳感器，通過JY61的處理器讀取MPU6050的測量數據然后通過串口輸出，靜態測量精度穩定在0.05°，動態精度為0.1°。實驗場景為9 m×21 m的實驗室，由3個UWB基站組成一個等腰三角形，所有基站在距地面高為2.40 m的同一平面上，UWB標簽置于機器人頂端。機器人實物系統如圖10所示。

圖10 實驗機器人的圖片

實驗分為5組，每組做5次實驗，每組實驗分別為單獨使用輪式里程計、在視距情況下單獨使用UWB、在視距情況下進行文中方法的融合、在存在8 m非視距情況下單獨使用UWB、在存在8 m非視距情況下進行文中方法的融合，以所得實驗數據分別作為定位坐標進行運動控制。利用UWB標簽加蓋來產生非視距情況。

理想實驗軌跡與仿真時的相同，一次實驗共運行20 m，平均運行時間為59.82 s，其中2～10 m區間段為產生非視距的區域。機器人以stm32f103單片機為控制器，進行數據處理和機器人控制。機器人每10 ms進行一次閉環糾偏,每次的糾偏距離是機器人當前坐標與終點和起點直線的垂直距離，即當前機器人偏離目標位置的距離。機器人將用這個偏離的距離作為輸入量，使用PID算法對機器人進行軌跡糾偏，以保證機器人回到目標路徑上。總糾偏距離可以反映機器人一段時間內運動的平穩性，總糾偏距離越小表明機器人運動越平穩，糾偏距離為零表示機器人保持在理想路徑之上。將所得實驗數據列于表1。

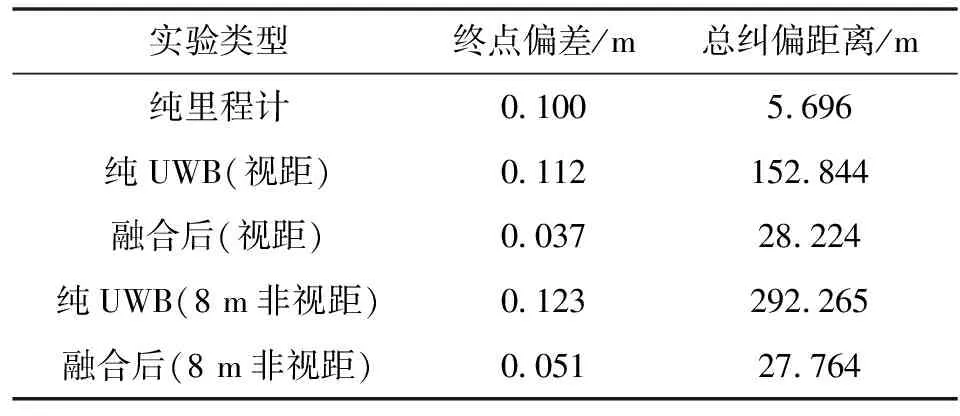
表1 得到的5組數據

由表1可以看出:單獨使用里程計的數據運動20 m平均產生了100 mm的終點偏差，這個誤差是長距離運動導致的累計誤差，且這個誤差會隨著運動距離的增加而增加，但里程計數據穩定，總糾偏距離只有5.696 m，機器人運行平穩。

使用純UWB數據進行定位的機器人運動過程中抖動極大，尤其是在非視距狀態下UWB數據極不穩定，終點偏差分別為112、123 mm，在視距狀態下運動20 m平均產生了152.844 m的總糾偏距離，在存在8 m的非視距狀態下運動更是平均產生了292.265 m的總糾偏距離，這表明單獨使用UWB數據不適合機器人定位。

使用文中算法在一直處于視距狀態下運動20 m終點偏差為37 mm，平均總糾偏距離為28.224 m，機器人運行較平穩。在存在8 m的非視距環境中運動20 m，終點偏差為51 mm，平均總糾偏距離為27.764 m，系統成功判斷出UWB是否處于非視距狀態并自動進行了不同信賴度的數據融合，大幅減小了UWB數據的抖動，并且將里程計數據的累計誤差控制在一定范圍內，得到的數據穩定且精度較高。相比單獨使用UWB的數據，在視距環境中穩定性提高了81.5%，精度提高了67.1%；在存在8 m非視距的環境中穩定性提高了90.5%，精度提高了59.2%。由此可見，使用文中融合方法可以大幅提高定位系統的穩定性和精度。

4 結論

本文作者利用里程計的短時精度高和UWB的長時誤差有界性，提出了一種基于卡爾曼濾波的數據融合方法，成功地將2種信息有機融合達到了長時高精度定位的目的。通過軟件仿真和實驗驗證表明：在UWB一直處于視距環境中融合后的數據相比單獨使用UWB的數據穩定性提高了81.5%，精度提高了67.1%；在存在8 m非視距環境中，相對于單獨使用UWB的數據穩定性提高了90.5%，精度提高了59.2%。系統運行穩定，實現了長時間連續可靠的定位，具有較大的工程應用價值。