FDM型3D打印機噴嘴多目標優化設計

任禮，白海清,2，鮑駿，賈仕奎，秦望，安熠蔚

(1.陜西理工大學機械工程學院，陜西漢中 723001；2.陜西省工業自動化重點實驗室， 陜西漢中 723001；3.陜西理工大學材料科學與工程學院，陜西漢中 723001)

0 前言

3D打印技術于20世紀80年代后期興起，美國某公司于2013年發布了題為“展望2025”的報告，稱3D打印技術屬于決定未來經濟的顛覆性技術。雖然國內該項技術起步較晚，總體水平仍落后于歐美國家，但近些年來，相關政府部門已出臺了一系列促進3D打印技術在國內發展的政策。目前，該項技術已是智能制造領域的重點研發方向之一。其中，熔融沉積(Fused Deposition Modeling，FDM)成型技術是3D打印技術的重要分支。其成型原理：將熱熔性材料加熱至熔融狀態后經細小的噴嘴擠出，物料逐層堆疊固化后最終成型。由于FDM型技術能夠更好地應用于個性化生產，成本低、耗材較為清潔且后處理便捷，因而得到了廣泛應用。但由于FDM型噴頭易堵塞，高精度噴頭被國外壟斷，導致高精度打印設備價格高昂，維護困難。為解決此類問題，學者們進行了許多研究。賈永臻等通過仿真試驗分析了噴嘴堵塞的成因，通過噴頭保溫措施有效改善了壓力分布。朱黎立等設計了3D打印機的冷卻裝置，以應對材料提前軟化和成型件冷卻不及時等問題，結合仿真分析與試驗驗證，提升了噴頭導絲性能和成型件精度。王利等人基于仿真模擬對FDM型打印機噴嘴的溫度場與應力場進行了分析，提出了防止噴嘴堵塞的具體措施。任翀等人基于FLUENT軟件對多種規格噴嘴進行了數值模擬，分析了不同送絲速率下的溫度場、速度場和壓力場。高強等人進行了正交仿真試驗，提出了噴嘴結構設計的最優方案。相關文獻對噴嘴的設計均提供了參考，但仿真試驗多設置為等溫分析或物料黏度為常量的情況，且個別結構一定程度上存在噴嘴微小孔加工精度難以保障等問題。然而，FDM型3D打印機噴嘴出口處流道結構存在突變，且噴嘴溫度對物料狀態也有直接影響，二者均能使熔體發生改變進而影響噴嘴的性能。目前，結構與溫度共同影響下，關于FDM型3D打印機噴嘴流固耦合傳熱分析與多目標優化設計的公開文獻相對較少，因而該方面的研究具有一定價值。

本文作者針對上述問題，將噴嘴結構特征與溫度作為變量，設計FDM型3D打印機噴嘴流固耦合傳熱正交仿真試驗；闡明試驗的設計方案以及結果；對噴嘴出口速度穩定性、流道熔體黏度以及出口壓力進行優化分析。使用極差分析法直觀地分析單因素影響下各指標的變化趨勢和影響程度，進一步采用Pareto遺傳算法對此多目標優化問題進行求解，并獲得能實現較優指標打印的噴嘴結構與工作溫度范圍。

1 數學模型與物理模型

1.1 數學模型

由于聚合物熔體流變行為的復雜性，建立描述流場的微分方程需要將部分微小影響因素忽略。假設如下：熔體充滿流道；熔體不可壓縮；忽略慣性力影響；忽略重力影響。

根據假設條件實現問題的簡化后，描述流場的微分方程如式(1)—(3)。

連續性方程：

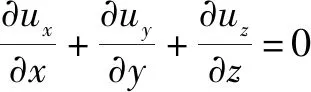
(1)

運動方程：

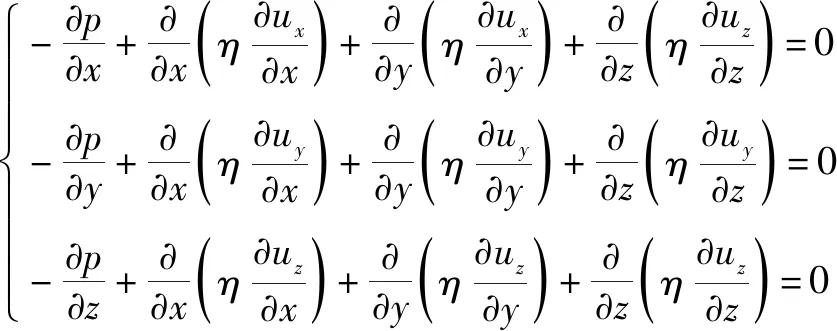
(2)

能量方程：

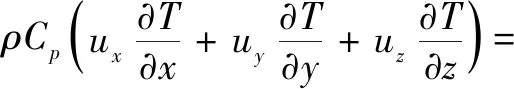
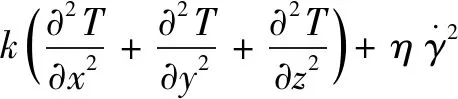
(3)

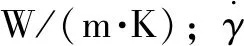
高聚物熔體的表觀黏度受剪切速率與溫度的共同影響，在FDM型3D打印工況下，噴嘴流道在出口處變小會使剪切速率大幅度提高，同時，噴嘴的溫度會影響分子無規則熱運動的程度，二者均對熔體黏度造成影響。因此，同時考慮剪切速率與溫度對熔體的影響才能準確描述噴嘴熔體的行為。為此，本文作者以Carreau模型描述熔體黏度隨剪切速率的變化規律，如式(4)所示。在此基礎上，以Approximate Arrhenius定律進行溫度修正，如式(5)所示，進而得到如式(6)所示的高聚物熔體度模型，并以聚丙烯(PP)為對象完成參數設置。

(4)

()=exp[-(-)]

(5)

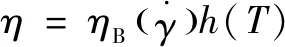
(6)

式中:為表觀黏度，Pa·s；為零表觀黏度，為26 470 Pa·s；為剪切速率影響下的物料黏度，Pa·s；為松弛時間，為2.15 s；為冪律指數，為0.38；為參考溫度，為473 K；為熱敏系數，為0.02 K。

1.2 物理模型

在基于螺桿擠出技術的FDM型3D打印過程中，熔體經過螺桿后以穩定的流率進入噴嘴并最終實現擠出。如圖1所示，根據噴嘴的結構特征，將影響熔體出口速度穩定性、黏度以及壓力損失的影響因素歸結為流道直徑、收縮角以及噴嘴溫度。為出口流道長度，使用較長時易造成噴嘴堵塞，它接近0時噴嘴加工精度難以保障且易磨損。綜合考慮，文中確定為0.5 mm，其余對流道影響微小的參數在試驗過程中亦保持恒定。

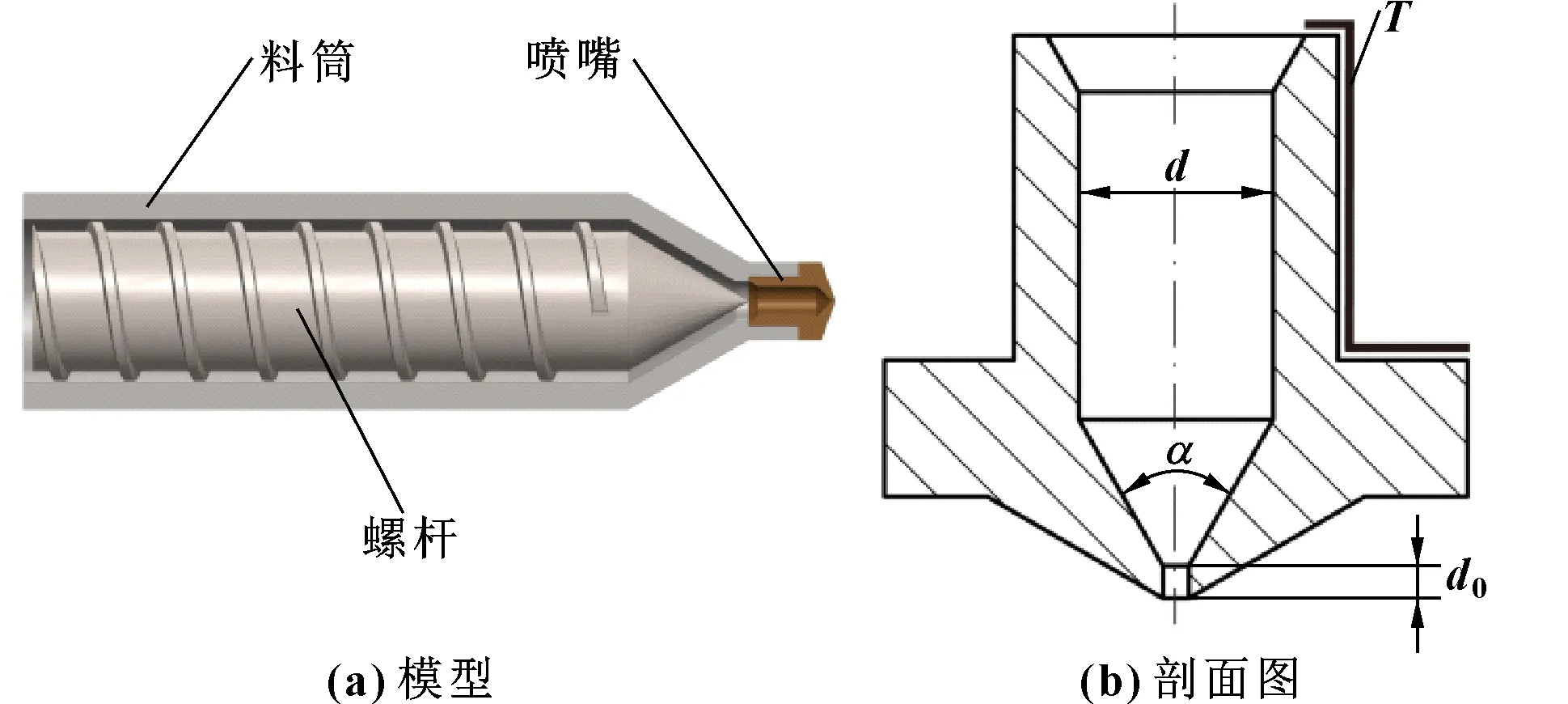
圖1 噴嘴結構

2 正交仿真試驗

2.1 試驗設計

為通過較少的試驗次數探究噴嘴結構參數與噴嘴溫度對熔體出口速度穩定性、流道流體黏度以及出口壓力的影響規律，根據噴頭規格與聚丙烯材料特性設計正交試驗，因素水平如表1所示。

表1 正交試驗因素水平

2.2 仿真試驗

2.2.1 網格劃分

建立正交試驗所需的9組合理簡化的噴嘴模型，圖2所示為其中1組試驗對應的模型和網格。在網格劃分過程中使流體與固體網格相耦合，由于二者結構均相對復雜，均以四面體進行劃分。對流體的外壁面設置膨脹層，對熔體出口位置進行進一步網格細化，最終形成如圖2所示的網格狀態。

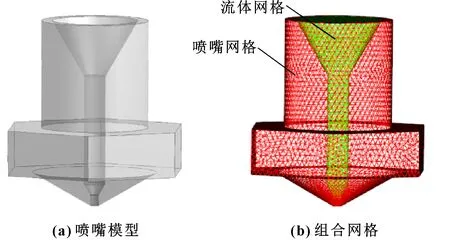
圖2 模型與網格

2.2.2 邊界條件設置

邊界條件分為流體域的運動邊界條件和熱邊界條件。

(1)運動邊界條件。參考傳統打印噴嘴結構設計，當出口直徑為0.4 mm、入口直徑為2 mm的噴嘴模型以0.1 mm厚度進行較高精度分層打印時，送絲速度為0.5 mm/s。通過式(7)得出對應流率為1.57 mm/s，并將它設定為入口邊界條件；設置流體外壁面無滑移；出口條件為法向力與切向速度為0。

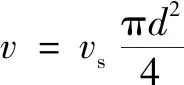
(7)

式中：為體積流率，mm/s；為送絲速率，mm/s；為噴嘴入口直徑，mm。

(2)熱邊界條件。設置流體入口溫度與噴嘴溫度相同，流體與固體交界面溫度與熱通量連續，流體出口無傳導熱通量；設置噴嘴材料為黃銅，熱導率為130 W/m· ℃；設置固體與料筒接觸面的溫度為常量，其余壁面與20 ℃室溫對流換熱。

3 仿真試驗結果與極差分析

3.1 試驗結果

正交仿真試驗結果如表2所示，在試驗結果的后處理中，重點以噴嘴出口面的速度分布、流道中心位置黏度均值以及出口面壓力值為研究對象。9組仿真試驗結果所形成的壓力場、速度場、黏度場、溫度場以及剪切速率場分布狀態趨同。以試驗1為例，結果如圖3所示。可以看出：出口面流體壓力總體穩定，與此同時，隨熔體流向出口的沿程壓力逐漸降低。由圖(c)可以看出：流體速度呈現中心高、周圍較低的分布狀態。結合圖(d)與圖(f)可以看出：狹小的流道剪切作用變強，因而熔體沿擠出方向總體呈降低趨勢，且由于靠近壁面的流體剪切速率較高，靠近壁面的熔體黏度明顯小于遠離壁面的熔體。由圖(e)可知:由于噴嘴與空氣對流傳熱程度小且黃銅的導熱系數較高，噴嘴溫度降低不明顯。

表2 正交試驗結果

圖3 試驗1結果

3.2 試驗結果極差分析

極差分析法又稱“直觀分析法”，操作便捷、實用性強，可快速確定因素對指標的影響程度與規律。計算公式為

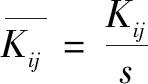
(8)

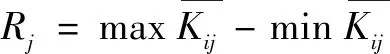
(9)

3.2.1 出口速度方差值分析

通過公式(8)(9)計算得到出口速度方差值的極差分析表如表3所示。可以看出：對出口速度穩定性影響最大的因素是流道直徑，隨流道直徑的增加，出口速度方差先增大而后趨于平穩，說明較小的流道直徑有利于保證噴嘴出口截面上速率整體穩定，但考慮到噴嘴制造的工藝性與避免噴嘴堵塞，流道直徑不宜小于1 mm。同時，收縮角的大小與噴嘴處的溫度對出口速度方差的影響不明顯。

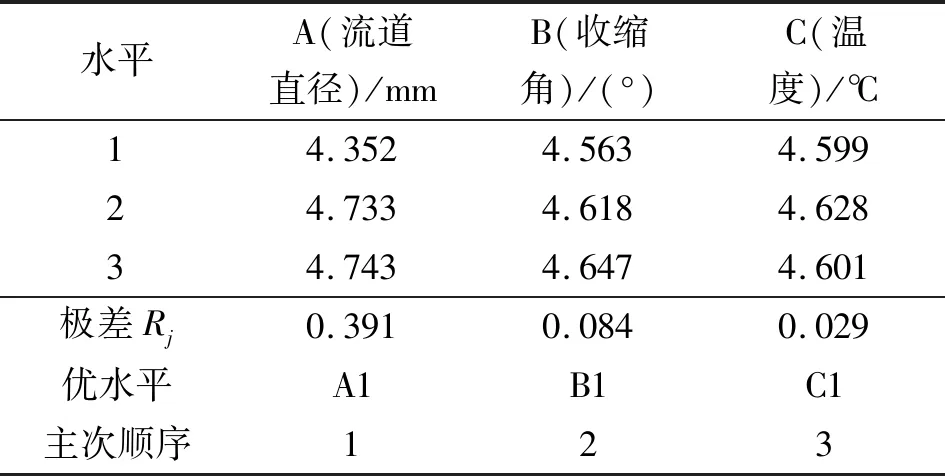
表3 出口速度方差值極差分析結果

3.2.2 流道熔體黏度分析

同理可得，流道熔體黏度的極差分析結果如表4所示。可以看出：三因素的變動均對流道流體黏度有較大的影響，影響程度由大到小依次為噴嘴溫度、流道直徑、收縮角。熔體黏度隨溫度上升而下降，隨其余兩因素增加而增加。分析可得，分子無規則熱運動隨溫度上升而加劇，從而使分子間距增大，材料內部形成了更多的自由體積，從而使高分子鏈段更容易活動，因而黏度降低。而流道直徑和收縮角的增加，使得由壁面產生的剪切作用降低，因而黏度升高。

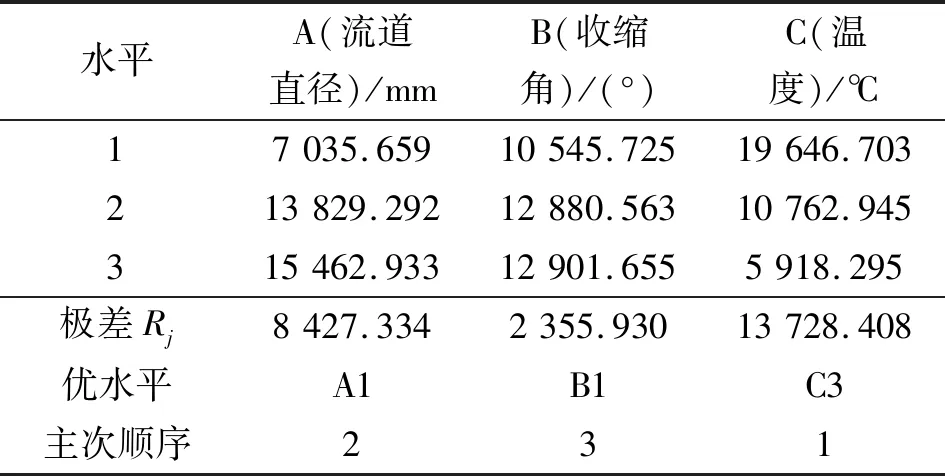
表4 流道流體黏度均值極差分析結果

3.2.3 出口壓力分析

同理可得，出口壓力的極差分析結果如表5所示，可以看出：相比其他因素，噴嘴溫度對出口壓力具有顯著影響，當溫度上升時出口壓力下降。在流率恒定的情況下，溫度升高會產生較大的壓力損失，使出口壓力降低。

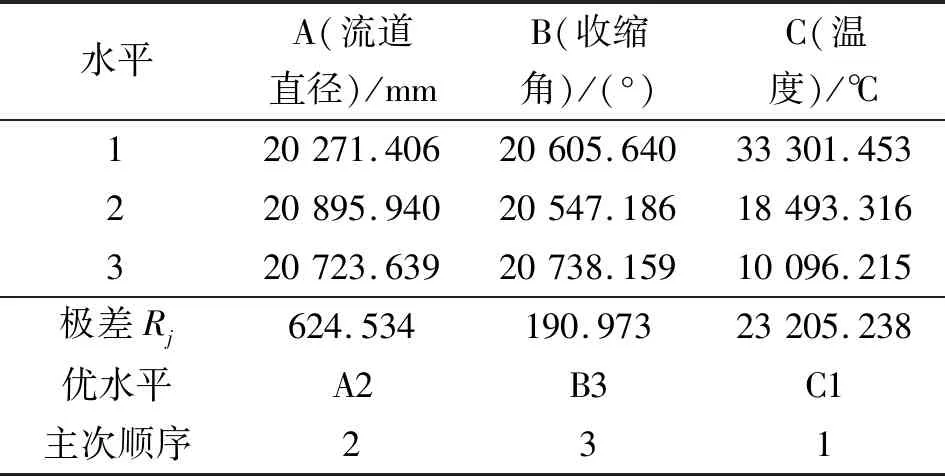
表5 出口壓力值極差分析結果

通過以上分析可得，出口速度方差、流道流體黏度以及出口壓力受試驗因素的影響程度各異。綜合考慮，以低出口速度方差、較低流道流體黏度以及較高出口壓力為優化目標，通過Pareto遺傳算法進行此多目標優化問題的求解。

4 基于Pareto遺傳算法的多目標優化

4.1 遺傳算法原理

遺傳算法依托生物進化過程中優勝劣汰的進化理論，實現優化問題中目標函數向優化解逼近的過程。通過選擇、交叉和變異的方法對群體進行更新，最終獲得滿足適應度函數的最優解。遺傳算法的運算流程如圖4所示。

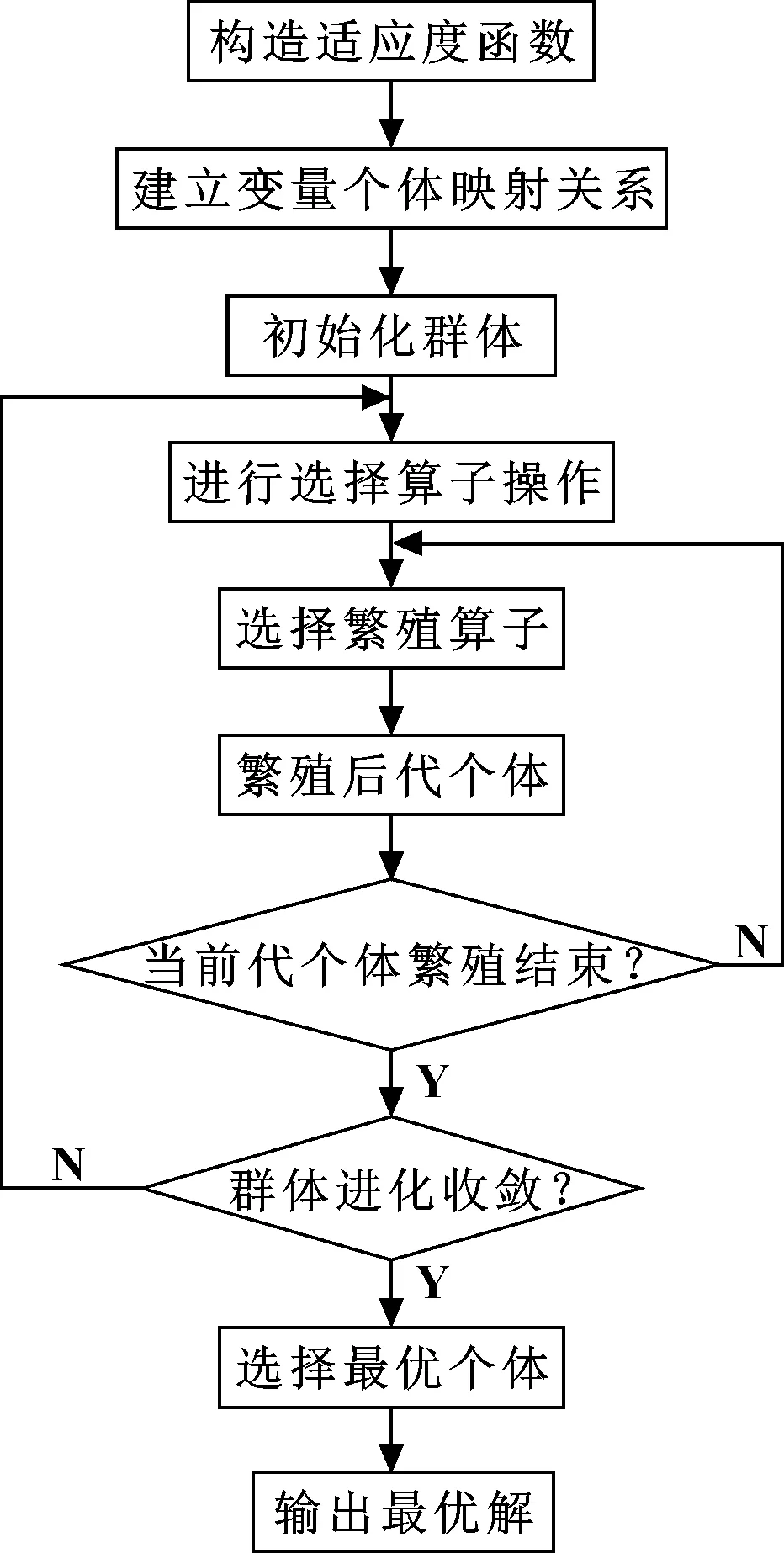
圖4 遺傳算法流程

4.2 多目標優化方法

求解多目標優化問題是工程領域的常見需求。由于多目標優化過程中各目標往往相互限制，很難同時達到最優。而遺傳算法能夠在充分考慮各因素的影響下，得出各指標都相對具有優勢的解集，進而為工程領域問題提供參考。定義多目標優化問題如式(10)—(11)所示：

min()=[(),(),…,()]∈

(10)

s.t.()≤0=1,2,…,

式中:=[,,…,]∈，為維決策變量；()為維目標函數；()為單個目標與自變量的關系表達式，即適應度函數，=1,2,…,,∈；≤0為第個不等式約束條件；為不等式約束個數。

4.3 構建適應度函數

使用遺傳算法進行優化計算時需要構建適應度函數。與自然界中更適應環境的物種易于繁殖的原理類似，遺傳算法中以適應度的概念來度量優化計算過程中每個個體可能達到、接近或有助于找到最優解的優良程度。

試驗中優化目標為出口速度方差、流道熔體黏度以及出口壓力，基于最小二乘原理，使用MATLAB軟件通過多項式擬合法對9組正交試驗數據進行擬合。為獲得擬合程度良好的回歸方程，將最高次項提高為三次。進而,分別得到自變量為、和的3個回歸方程，并將它們作為遺傳算法計算使用的適應度函數。

建立出口速度方差值回歸模型：

=3330 6-0677 8+0018 9+0010 4-

0028 1-0000 000 657-0000 020 7-

0000 004 58

(11)

使用檢驗法對回歸方程進行檢驗，(7，1)=14 312.8，遠大于臨界值(7，1)=236.8，回歸方程可以使用。

建立流道熔體黏度模型:

=1 415726 4+93 609931 9-641755 3+

0253 8-1 517371 1+28232 4+

0994 7-0120 5

(12)

同理，(7，1)=131 648，遠大于臨界值(7，1)=236.8，回歸方程可以使用。

建立出口壓力值回歸模型:

=292 914112 8+5 137209 1-

2 055001 7+47025 1-32168 3+

2864 5-1651 1+3953 6

(13)

同理，(7，1)=17 811.3，遠大于臨界值(7，1)=236.8，回歸方程可以使用。

4.4 目標函數

構建自變量優化模型矢量表達式如式(14)所示，目標優化的自變量分別為流道直徑、收縮角以及溫度。

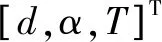
(14)

記出口速度、流道流體黏度以及出口壓力回歸方程分別為()、()與()，以較小的出口速度方差與流道流體黏度以及較大的出口壓力為優指標，使用求解最小值的優化法，因而出口速度方差與流道流體黏度取最小值，即為min()、min()，出口壓力求取為min(-())。優化目標函數如式(15)所示:

(15)

4.5 約束條件

基于正交試驗參數的選取范圍對自變量、、取值范圍進行約束，分別為流道直徑范圍約束如式(16)所示，收縮角范圍約束如式(17)所示以及噴嘴溫度約束如式(18)所示。

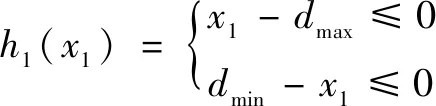
(16)

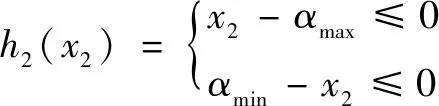
(17)

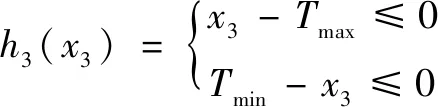
(18)

因而，自變量、、取值的邊界約束條件如式(19)所示：

()=[(),(),()]

(19)

綜上所述，噴嘴結構參數的多目標優化模型為

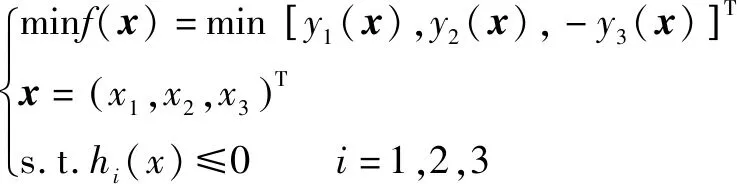
(20)

4.6 求解優化模型

根據噴嘴規格以及聚丙烯材料擠出加工特性，確定噴嘴結構參數以及噴嘴溫度取值范圍如式(21)所示。基于遺傳算法，使用MATLAB軟件編寫M文件進行求解，所得Pareto前端三維解集如圖5所示。

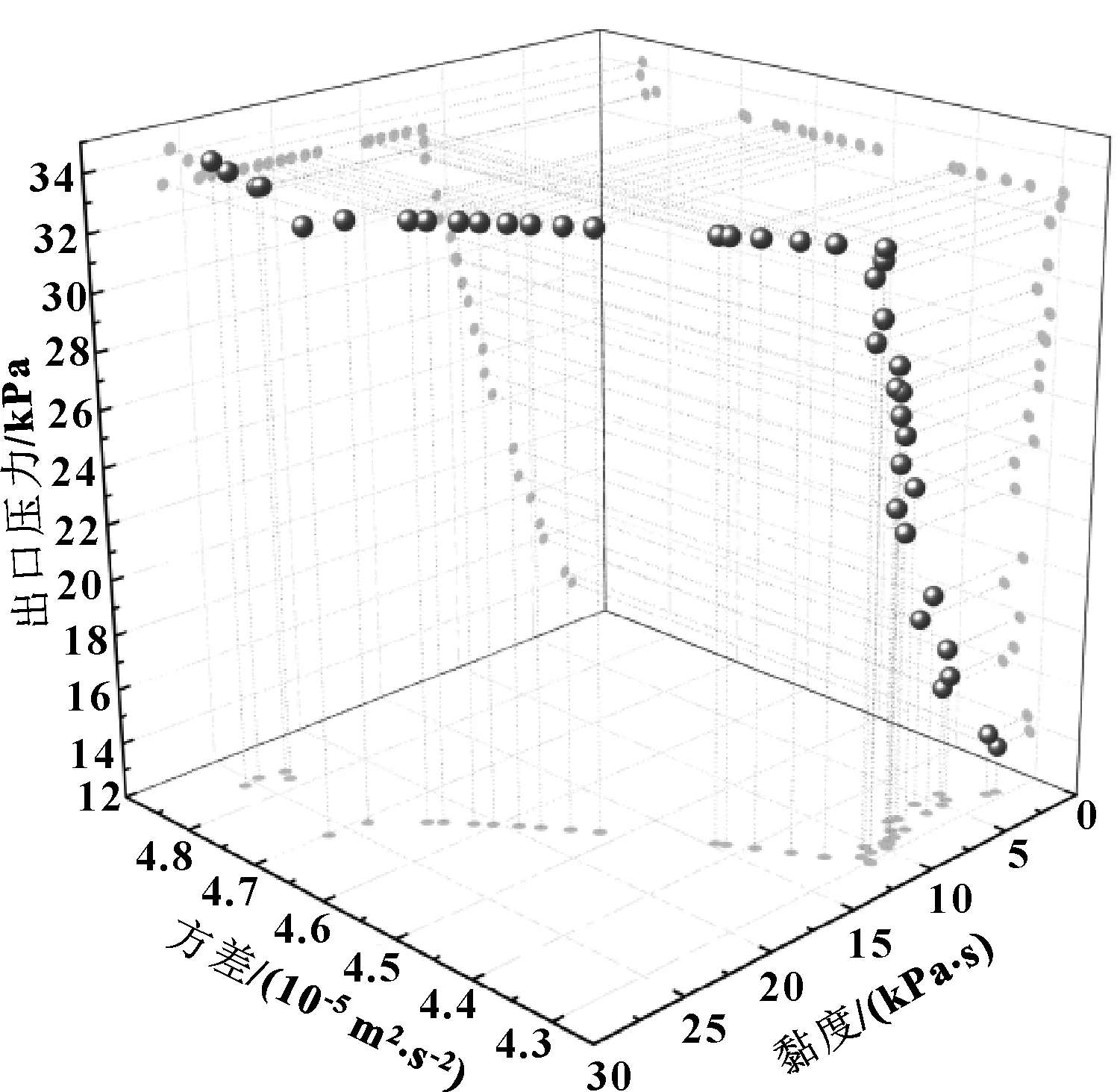
圖5 Pareto前端解集

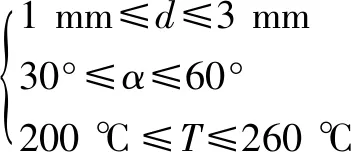
(21)

5 優選結果

分析結果可得，解集中的優選參數產生在噴嘴流道直徑為1 mm、收縮角為30°、溫度為200～210 ℃的情況下。表6中列舉了優選參數的仿真結果。可知：熔體出口面速度方差處于較低水平，出口面速度保持較為均一的水平，提高了打印精度；與此同時，流道內部較低的熔體黏度以及較高的出口壓力能夠保證噴嘴熔體擠出時具有較好的流動性，有利于打印過程的穩定進行。

表6 3組試驗結果對比

6 結語

使用Polyflow軟件，進行了FDM型3D打印機噴嘴流固耦合傳熱正交仿真試驗。以提高打印精度和噴嘴熔體流動性為目標，以流道直徑、收縮角與噴嘴溫度為試驗變量，并以較小的噴嘴出口速度方差、較小的流道熔體黏度以及較大出口壓力值作為優化指標，通過分析流場云圖，得出噴嘴熔體壓力場、速度場、黏度場、溫度場以及剪切速率場的分布趨勢；進一步，通過對流場各項數據的提取與分析，可以得到以下結論：

(1)通過對正交仿真試驗結果的極差分析，可以分別得出三因素作用下每個指標的變化程度，其中，流道直徑是出口速度方差最顯著的影響因素，流道熔體黏度與出口壓力兩指標最顯著的影響因素是熔體溫度；

(2)基于遺傳算法對打印機噴嘴的多目標優化問題進行求解，并考慮噴嘴實際的工藝性，得出具有1 mm直徑的流道、30°收縮角的噴嘴在200～210 ℃工作時，打印聚丙烯熔體能夠實現較優的綜合指標。