基于自適應(yīng)滑模控制的刀盤伸縮系統(tǒng)研究

張杭軍，方錦輝，楊宇柱，胡惠兵

(浙江大學(xué)流體動力與機電系統(tǒng)國家重點實驗室，浙江杭州 310027)

0 前言

近年來，隧道掘進機廣泛應(yīng)用于隧道施工中，成為地下空間開發(fā)的利器。泥水平衡盾構(gòu)能滿足復(fù)雜地層、高水壓、長距離工程建設(shè)需求，是目前穿江越河隧道工程的首選機型。同時，泥水盾構(gòu)也面臨著更多的挑戰(zhàn)：刀具磨損更換問題，復(fù)雜地層盾構(gòu)受困等。為了解決這些問題，中鐵裝備、鐵建重工、浙江大學(xué)等單位研究設(shè)計了如圖1所示的新型刀盤伸縮機構(gòu)。刀盤固定在驅(qū)動箱上，并由驅(qū)動箱內(nèi)多個電動或者液壓馬達驅(qū)動。驅(qū)動箱通過軸承連接到盾構(gòu)主架。在驅(qū)動箱的背板上安裝了多個呈圓形分布的伸縮缸，伸縮缸的另一側(cè)連接支撐座。如果這些液壓缸同步伸縮，則驅(qū)動箱將在軸承內(nèi)環(huán)帶動刀盤向前或向后移動，實現(xiàn)刀盤超挖，輔助換刀或者盾構(gòu)脫困。另外，在驅(qū)動箱的兩側(cè)對稱裝有導(dǎo)向塊，刀盤和驅(qū)動箱的反扭矩通過導(dǎo)向塊傳遞到盾構(gòu)主架，以提供反向支撐、伸縮導(dǎo)向并防止驅(qū)動箱在掘進過程中旋轉(zhuǎn)。

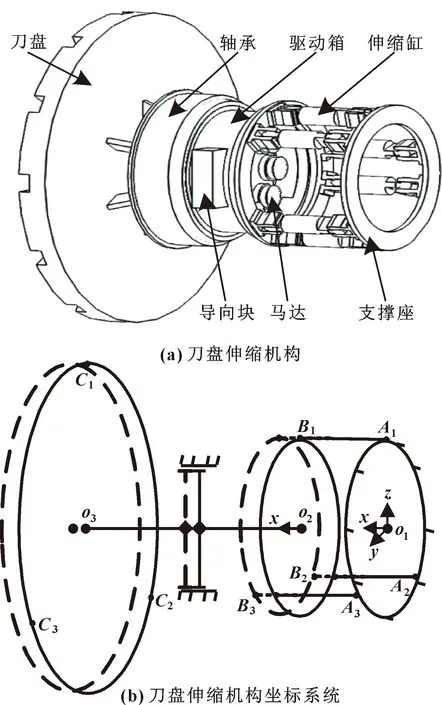
圖1 刀盤伸縮機構(gòu)示意

盾構(gòu)超挖的質(zhì)量由刀盤實際運動軌跡和設(shè)計軌跡的偏差決定，而刀盤運動軌跡由伸縮缸實時控制。因此，精確控制伸縮缸是減少超挖誤差和提高隧道施工安全性的重要技術(shù)。但電液系統(tǒng)存在很強的非線性，如閥口-非線性關(guān)系、隨溫度壓力變化的油液特性等。電液系統(tǒng)也存在參數(shù)不確定性，如阻尼系數(shù)、時變負載等。這些特征增加了電液系統(tǒng)控制的難度。為了獲得更好的動態(tài)特性，越來越多的研究人員研究非線性控制算法來補償系統(tǒng)中的非線性和不確定性。在工作點附近使用極點配置將非線性系統(tǒng)局部線性化，但在全局范圍內(nèi)不能得到滿意的控制效果。滑模控制被廣泛應(yīng)用于電液控制系統(tǒng)中，滑模面的動態(tài)行為不受參數(shù)不確定和外界干擾影響，但其控制輸入的固有振顫會引發(fā)系統(tǒng)高頻抖動。自適應(yīng)控制的提出與應(yīng)用有效地解決了模型不確定的影響，但其抗干擾能力較弱。 YAO和TOMIZUKA設(shè)計了一種自適應(yīng)魯棒控制，有效地集成了自適應(yīng)控制和確定性魯棒控制。YAO、LYU等將自適應(yīng)魯棒控制器應(yīng)用于具有非線性和模型不確定性的液壓執(zhí)行器的軌跡跟蹤，并取得了滿意的結(jié)果。結(jié)合刀盤伸縮控制的難點，為提高刀盤伸縮機構(gòu)在復(fù)雜地層中的精度和穩(wěn)定性，提出一種將滑模控制和自適應(yīng)魯棒控制相結(jié)合的非線性控制，包括具有特殊自適應(yīng)律的位置跟蹤閉環(huán)，能補償不確定的負載。通過李雅普諾夫函數(shù)驗證閉環(huán)系統(tǒng)的穩(wěn)定性，并通過AMESim和Simulink聯(lián)合仿真進行模擬試驗，驗證該策略的有效性。

1 伸縮缸建模

刀盤伸縮系統(tǒng)并非實時工作，當(dāng)需要更換刀具或者刀盤受困時適時啟動，通過伸縮油缸帶動刀盤前后運動實現(xiàn)超挖。單區(qū)伸縮缸的控制回路如圖2所示，減壓閥調(diào)定比例伺服閥的入口壓力，比例伺服閥精確控制進出伸縮缸的流量和壓力，平衡閥防止伸縮缸失速。伸縮缸的力平衡方程為

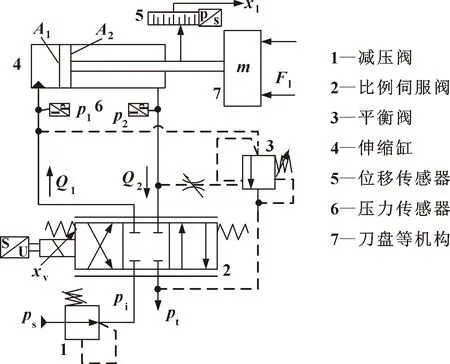
圖2 伸縮缸液壓示意

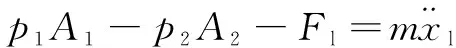
(1)

式中：和分別為伸縮缸無桿腔、有桿腔的壓力；和分別為伸縮缸無桿腔、有桿腔的作用面積；為負載集中參數(shù)，包括刀盤負載、阻尼力、摩擦力等；為不確定的負載質(zhì)量；為伸縮缸的位移。

伸縮缸的流量連續(xù)性方程為

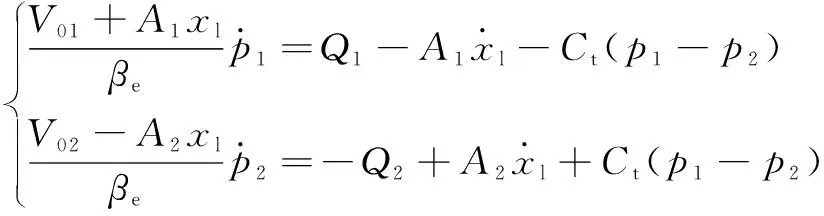
(2)

式中：和分別為伸縮缸無桿腔、有桿腔初始體積；為工作油液有效彈性模量；為伸縮缸內(nèi)泄漏系數(shù)，若采用零泄漏缸，可以忽略內(nèi)泄漏；為從伺服比例閥流向伸縮缸無桿腔的流量；為從比例伺服閥流向伸縮缸有桿腔的流量。

比例伺服閥口的流量可以寫成：

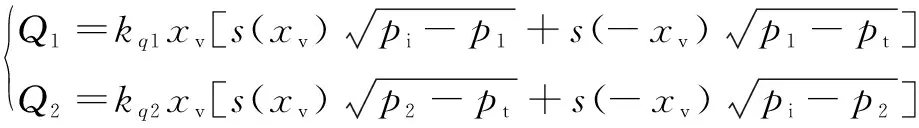
(3)

其中：

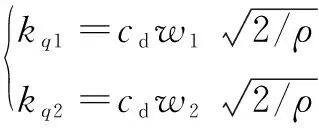
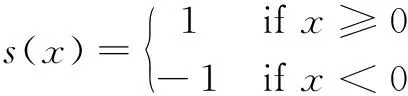
(4)

式中：1和2分別為比例伺服閥A、B口流量增益；為比例伺服閥的閥芯位移；為減壓閥設(shè)定壓力，即比例伺服閥P口壓力；為比例伺服閥回油壓力；為流量系數(shù)；和分別為比例伺服閥A、B口面積梯度；為工作油液密度。

由于伸縮缸系統(tǒng)的響應(yīng)頻率遠遠小于比例伺服閥的響應(yīng)頻率，可以忽略比例伺服閥的動態(tài)響應(yīng)環(huán)節(jié)，將它視為比例過程：

=

(5)

式中：為電壓位移增益；為控制輸入電壓。

將式(5)代入式(3)，得到新的閥口流量公式：

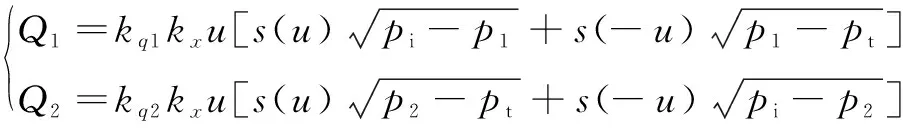
(6)

2 非線性控制器設(shè)計

定義系統(tǒng)狀態(tài)變量為

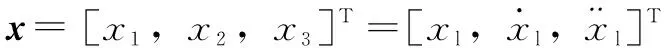
(7)

整合式(1)、(6)和(7)可以得到系統(tǒng)狀態(tài)方程：

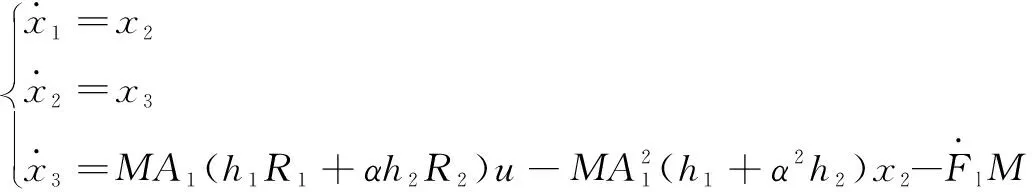
(8)

其中：

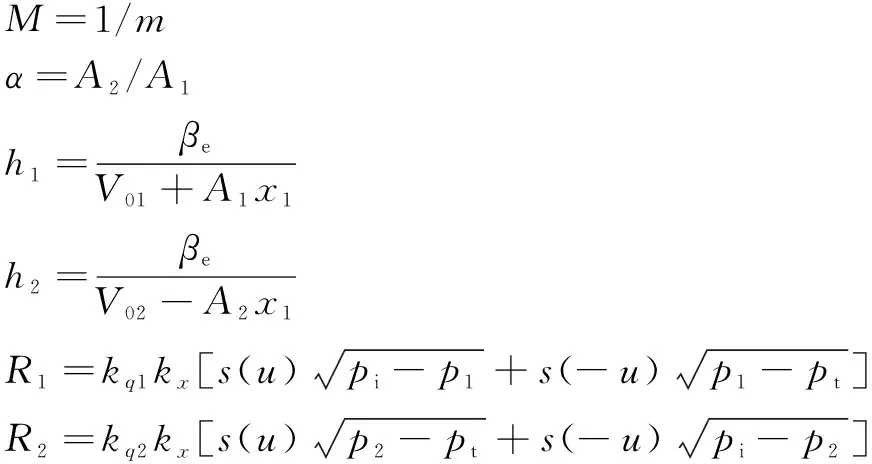
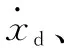
>>>0,>>>0

(9)

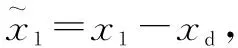
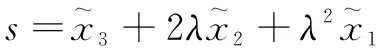
(10)

式中：為調(diào)節(jié)系數(shù)，為正常數(shù)。如果滑模面很小或者趨近于0，那么跟蹤誤差也會很小或者趨近于0。

對式(10)進行微分，得到其導(dǎo)數(shù)為

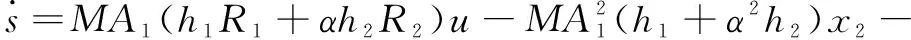
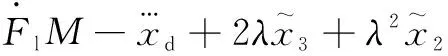
(11)

設(shè)計控制輸入結(jié)構(gòu)為

=+

(12)

式中：是為了滿足軌跡跟蹤而設(shè)計的可調(diào)節(jié)參數(shù)適應(yīng)項；是魯棒控制項。可以設(shè)為

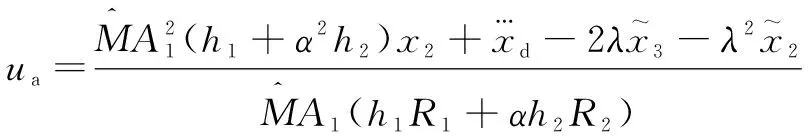
(13)

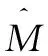
將式(13)代入式(11)中，可以得到：

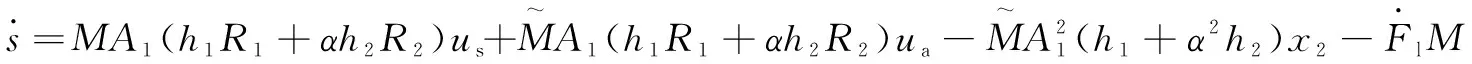
(14)

假設(shè)名義質(zhì)量是有界的，且負載集中參數(shù)對應(yīng)的加速度微分項也是有界的，則：

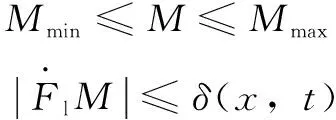
(15)

設(shè)計魯棒控制項的結(jié)構(gòu)為

=+

(16)

式中：為線性反饋項，用于系統(tǒng)穩(wěn)定調(diào)節(jié)；為非線性魯棒反饋項。可以設(shè)為

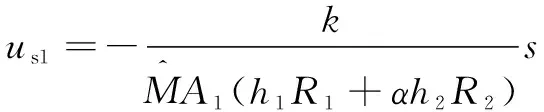
(17)

式中：為線性反饋系數(shù)，為正常數(shù)。

把式(17)代入式(14)中，可以將其化簡為

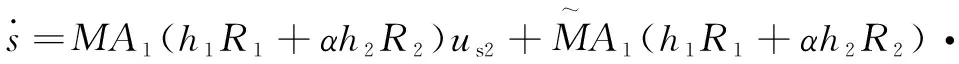
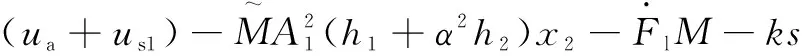
(18)

設(shè)一個約束函數(shù)(,)：

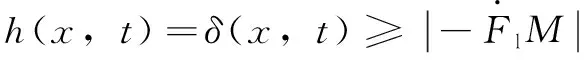
(19)

可以設(shè)為

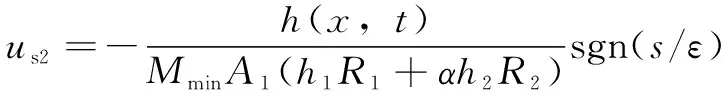
(20)

其中：

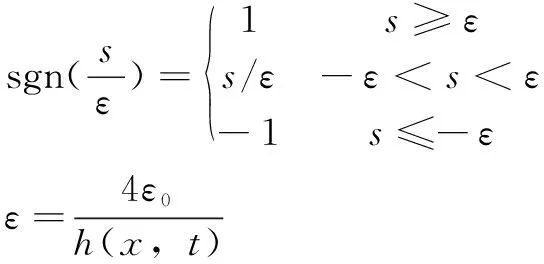
(21)

式中：為一個可以任意小的參數(shù)。

定義李雅普諾夫函數(shù)為

=12

(22)

對式(22)進行求導(dǎo)，并將式(18)代入，得：

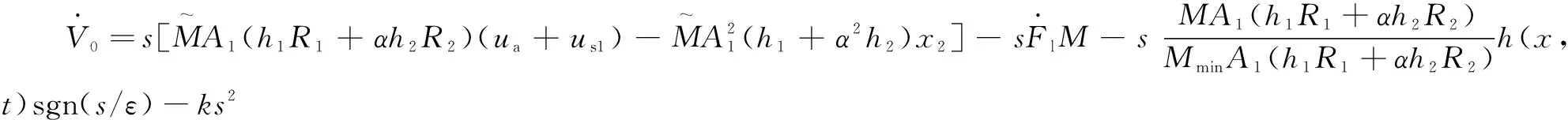
(23)

名義質(zhì)量的自適應(yīng)率可以設(shè)為

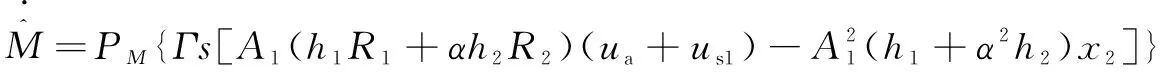
(24)

其中：

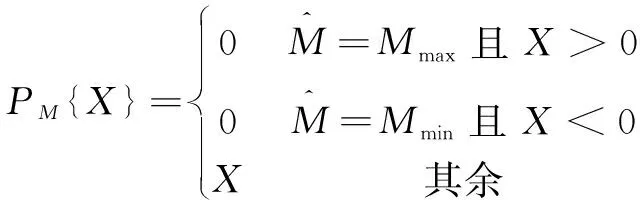
(25)

式中：是一個正常數(shù)。

定義李雅普諾夫函數(shù)為

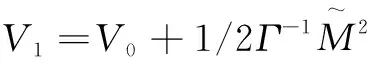
(26)

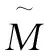
對式(26)進行微分，并將式(23)代入，得到：

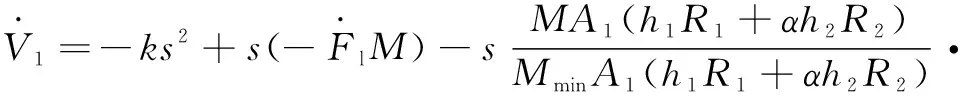
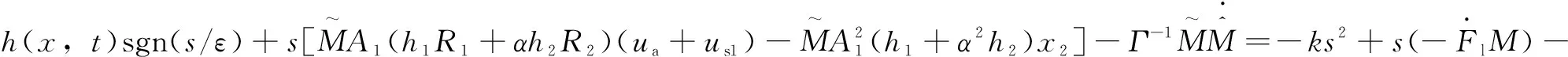
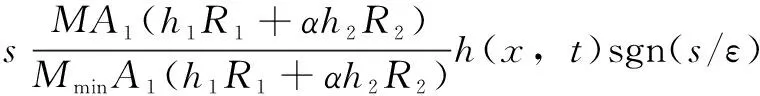
(27)

假設(shè)名義質(zhì)量是一個未知的常數(shù)或者其變化率較低，那么的導(dǎo)數(shù)可以認為是0。

若滑模面滿足||≥，則：

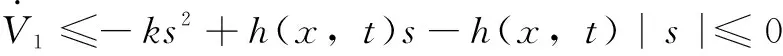
(28)

若滑模面滿足||<, 則：

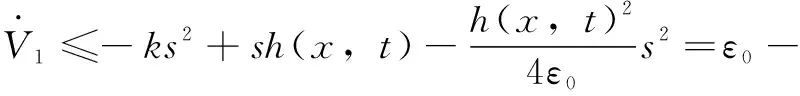
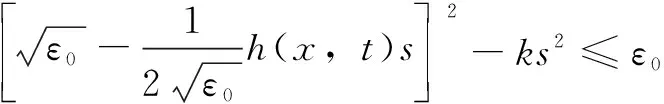
(29)

比例伺服閥的控制輸入為

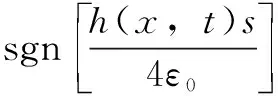
(30)

通過李雅普諾夫函數(shù)證實了包括非線性控制器和電液系統(tǒng)在內(nèi)的整個閉環(huán)回路的穩(wěn)定性。在有限的時間內(nèi)，伸縮缸的跟蹤誤差趨近0。

3 仿真結(jié)果

為驗證上述算法的有效性，進行AMESim和Simulink的聯(lián)合仿真。圖3為模擬試驗臺示意圖，主要包括3支伸縮缸、3支負載缸和配套系統(tǒng)。每1支伸縮缸都由自身比例伺服控制回路控制；負載缸施加負載，模擬真實土層阻力。

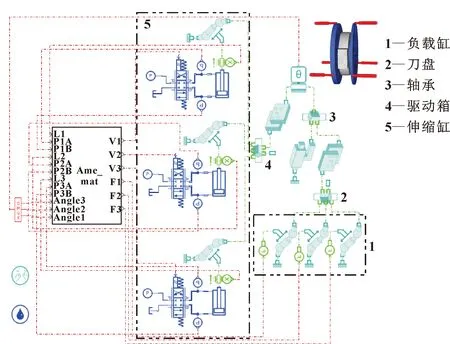
圖3 刀盤伸縮系統(tǒng)模擬試驗臺示意

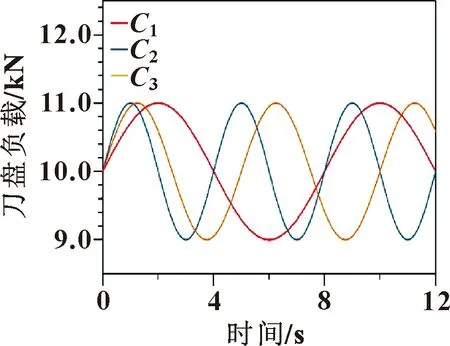
圖4 刀盤負載力

、、為伸縮缸在支撐座側(cè)坐標點，、為伸縮缸在驅(qū)動箱側(cè)坐標點，、、為刀盤負載作用點坐標，具體如式(31)所示：

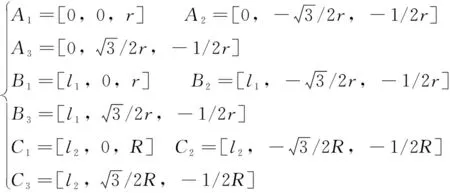
(31)

式中：為驅(qū)動箱、支撐座的半徑；為刀盤的半徑；為到的距離；為到的距離。

非線性控制器參數(shù)和模擬系統(tǒng)參數(shù)如表1所示。

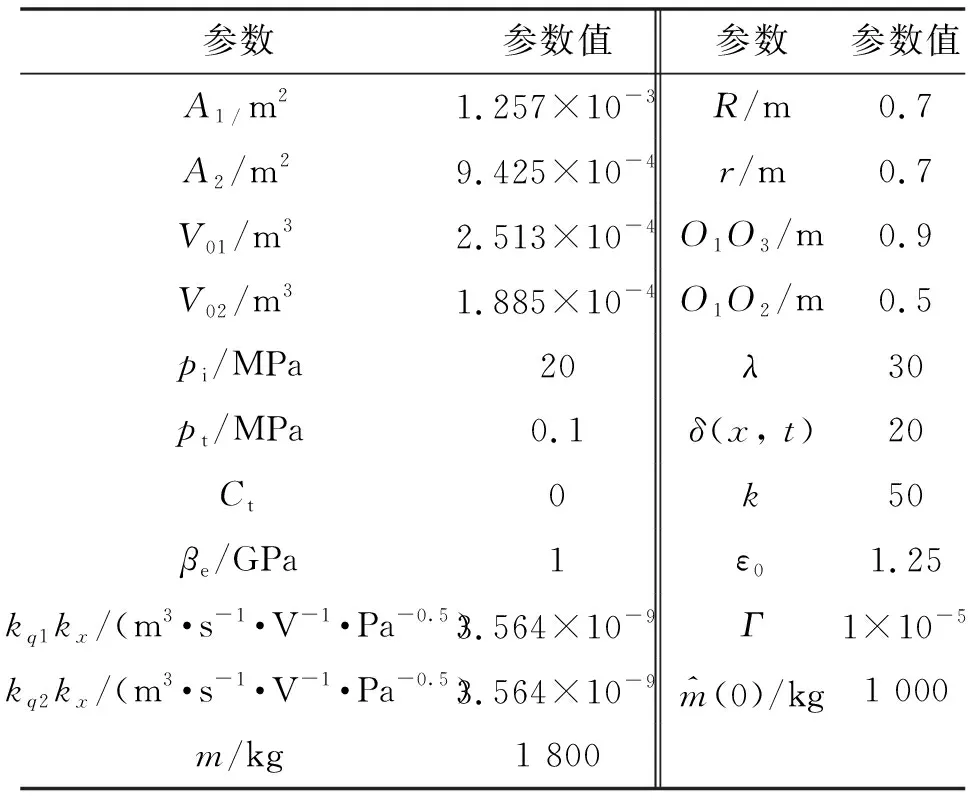
表1 控制器參數(shù)和模擬系統(tǒng)參數(shù)

3支伸縮缸的目標位移為

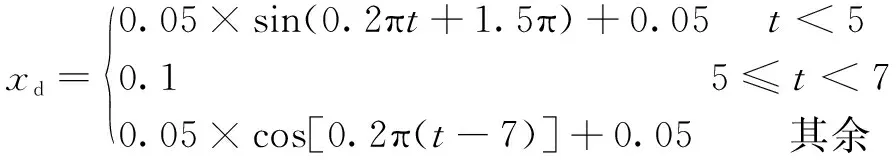
(32)

載質(zhì)量的初始估計值為1 000 kg，作用在刀盤上的負載如圖4所示。負載是不同頻率的正弦力，作用在刀盤上致使刀盤抖動。設(shè)計伸縮缸同步伸出和縮回，目標軌跡如式(32)所示，非線性控制器合成比例伺服閥的輸入電壓，驅(qū)使伸縮缸跟隨目標軌跡。圖5所示為比例伺服閥的控制信號，輸入電壓是合理的，不存在高頻振蕩和長時間過飽和，這為后續(xù)伸縮缸平滑響應(yīng)奠定了基礎(chǔ)。圖6所示為工作過程中伸縮缸兩腔壓力，壓力符合假設(shè)約束在0～20 MPa。圖7所示為滑模面參數(shù)。可知：值保持在±0.5內(nèi)，位移、速度和加速度都能實現(xiàn)良好的跟隨，且跟隨誤差較小。圖8所示為質(zhì)量估計的過程，在1 s內(nèi)實現(xiàn)未知質(zhì)量的近似估計。圖9所示為3支伸縮缸的位移響應(yīng)和跟蹤誤差。可知：在開始時，伸縮缸并沒有實現(xiàn)跟隨，主要由于控制系統(tǒng)的初始化參數(shù)和模擬系統(tǒng)參數(shù)存在較大差異，但在0.1 s內(nèi)實現(xiàn)了調(diào)整，其后3支伸縮缸都得到了控制，實現(xiàn)了跟蹤并保持誤差在±0.1 mm內(nèi)。運行過程中最大跟蹤誤差出現(xiàn)在縮回速度最大點；5～7 s內(nèi)，伸縮油缸保持不動，穩(wěn)態(tài)誤差保持在±2 μm內(nèi)。由此可知，全過程中每一支伸縮缸都得到了精確控制，刀盤按照設(shè)計實現(xiàn)擴挖。

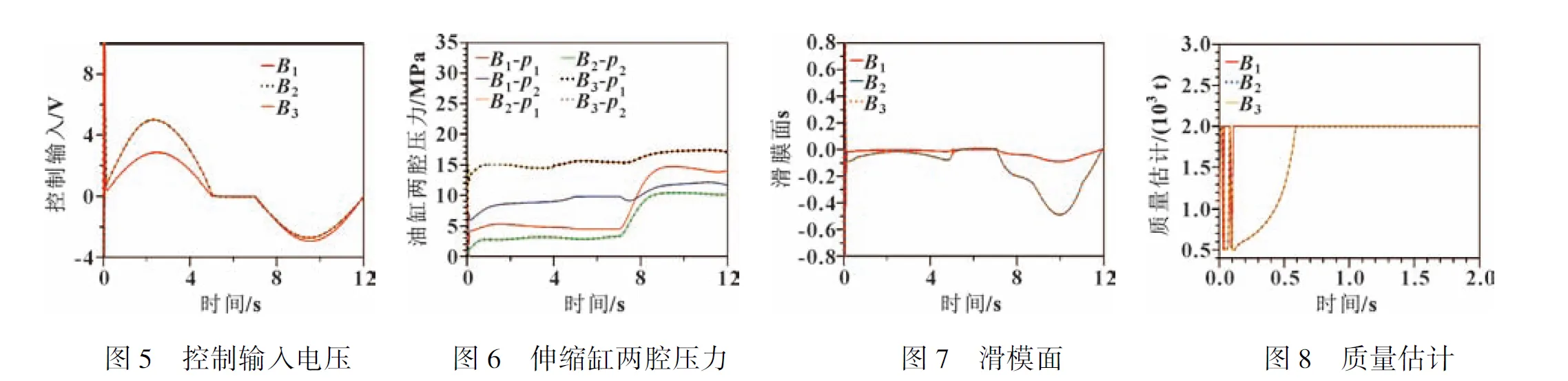
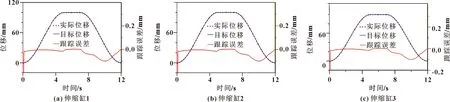
圖9 實際位移、目標位移與跟蹤誤差

AMESim和Simulink聯(lián)合仿真證實了所提算法的有效性，它不單單能實現(xiàn)精確控制，完成跟隨軌跡任務(wù)，也具有良好的自適應(yīng)性。

4 結(jié)論

本文作者提出了基于自適應(yīng)滑模控制的泥水盾構(gòu)刀盤伸縮系統(tǒng)，滑模控制和自適應(yīng)魯棒控制相結(jié)合的非線性控制不僅可以補償不確定的負載，而且具有很高的控制精度。通過李雅普諾夫理論驗證了控制器的穩(wěn)定性，并通過AMESim和Simulink聯(lián)合仿真證明了其優(yōu)異的性能。