基于光滑急動S曲線的激光鋼坯標識機構軌跡規劃
趙忠祥,潘存海,張帥鵬,李嘉文
(1.天津科技大學機械工程學院,天津 300222;2.天津市輕工與食品工程機械裝備集成設計與在線監控重點實驗室,天津 300222)
0 前言
傳統的鋼坯標識設備主要有撞號機、涂料噴涂標識設備、電弧噴涂設備和高能束噴涂標識設備等。而激光直接零部件標識(Laser Direct Part Marking)技術是一種在工業環境中證實可行、可實現高度自動化且綠色環保的標識技術,已經成為工業產品追溯中產品標識的重要手段。新型鋼坯標識設備以多軸機械手為傳動機構、激光打標機為核心部件對鋼坯進行準確標識。
根據標識運動過程的不同,標識模式分為固定標識和飛行標識。固定標識即將標識設備運動到某一點后進行靜態打標,要求運動結束后標識設備定位準確,并且殘余振動小、在運動結束后能立刻進行標識而不需要額外的等待時間。飛行標識是標識機構在運動過程中對多個分立的產品進行動態打標,要求飛行過程中,標識機構快速進入運動平穩階段,沒有晃動,因此需要快速達到勻速段,即要求加速和減速時間短。同時,要保證機構運動過程中急動曲線的連續,以免產生較大的啟停振動,但倍福PLC內置的梯形加減速曲線明顯不能滿足上述要求。因此,基于倍福PLC開發適合鋼坯標識過程的軌跡規劃算法很有必要。
標識機構軌跡規劃算法直接影響最終的標識結果。梯形速度剖面雖然可達到時間最優,但它在理論上具有無限大沖擊峰值的缺點,并且加速度曲線并不連續。S速度剖面曲線被限制在有限的加速度和沖擊范圍內,沖擊曲線不連續,容易在結束位置產生殘余振動。而高階多項式S曲線、正弦S曲線和諧波S曲線具有連續且光滑的急動曲線,能保證開始和結束時刻急動值為0,即殘余振動更小,適合此研究平穩、準確的要求。
本文作者介紹激光鋼坯標識機構的運動學模型,比較正弦和諧波2種不同類型急動剖面的特點;給出諧波AS曲線的時間參數確定算法,并引入加速段和減速段的比率參數以簡化模型;進一步比較兩類存在勻速段的正弦S曲線,以找出勻速段占比更大的適合飛行標識任務的曲線類型;給出PLC程序數據轉換時對精度的三次補償策略,并在直角坐標機械手上進行試驗驗證。
1 直角坐標機械手運動學建模
采用滾珠絲杠結構將直角坐標機械手3個關節的平動轉換成3個伺服電機的轉動,并通過倍福PLC帶動伺服驅動器進行運動控制。其運動學模型如圖1所示。固定標識時3個軸同時運動,在對每個軸分別進行軌跡規劃后需要進行三軸同步,以保證同時到達指定位置。激光打標器有一定的標識工作范圍,因此在飛行標識時應保證激光打標器與鋼坯端面距離恒定。基于上述任務要求,飛行標識時軸1運動到方向某一位置后,軸2、軸3同時運動,帶動安裝在工具坐標系的激光打標機對平面上多個鋼坯端面進行平動標識。

圖1 直角坐標機械手運動學模型
2 正弦和諧波急動輪廓比較
正弦和諧波S曲線不僅克服了高階多項式S曲線表達式復雜、難以實時進行運動控制的缺點,同時具有曲線無限可微、急動輪廓與高階多項式S曲線急動輪廓一樣光滑的優點。典型的正弦和諧波S曲線急動輪廓的表達式分別為
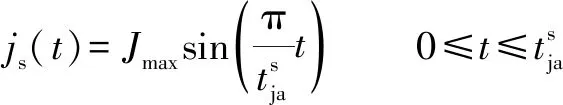
(1)

(2)
如圖2所示,正弦和諧波S曲線的急動輪廓具有不同的分布特性,因此得到的軌跡規劃曲線適用于不同的運動場合。
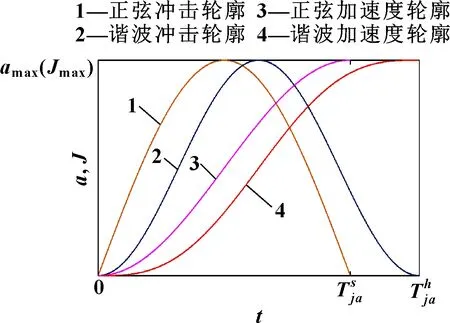
圖2 正弦和諧波S曲線沖擊輪廓比較
由圖2可知:當兩種曲線以相同的急動限制值達到相同的加速度限制值時,顯然諧波S曲線更加平緩但付出了更多的運動時間和運動距離。因此諧波S曲線更適合于要求啟停平穩尤其是停止時殘余振動小的固定標識任務,而正弦S曲線適合于要求有較小加速、減速時間和距離的飛行標識任務。
3 諧波AS曲線的時間參數確定
為獲得具有低殘余振動強度的精確定位,期望執行機構具有快速啟動和緩慢、平滑的停止。因此,在設計具有這種運動學特征的輸入時,需要不對稱的速度剖面。典型的不對稱諧波AS曲線如圖3所示,軌跡規劃重點在于在給定的運動學約束范圍內合理規劃各時間段參數以及找出產生各類曲線的位移邊界值。為簡化軌跡規劃模型,引入加速段和減速段的比率參數,其中、、和中有3個獨立參數和1個相關參數,相關參數可由獨立參數確定。
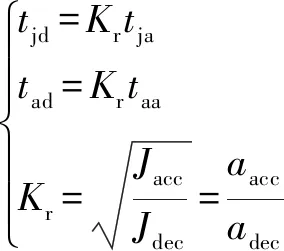
(3)
(1)能達到速度最大值,同時達到加速度最大值和時,則有:

(4)
其中:能達到這種情況的最小位移
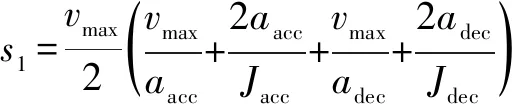
(5)
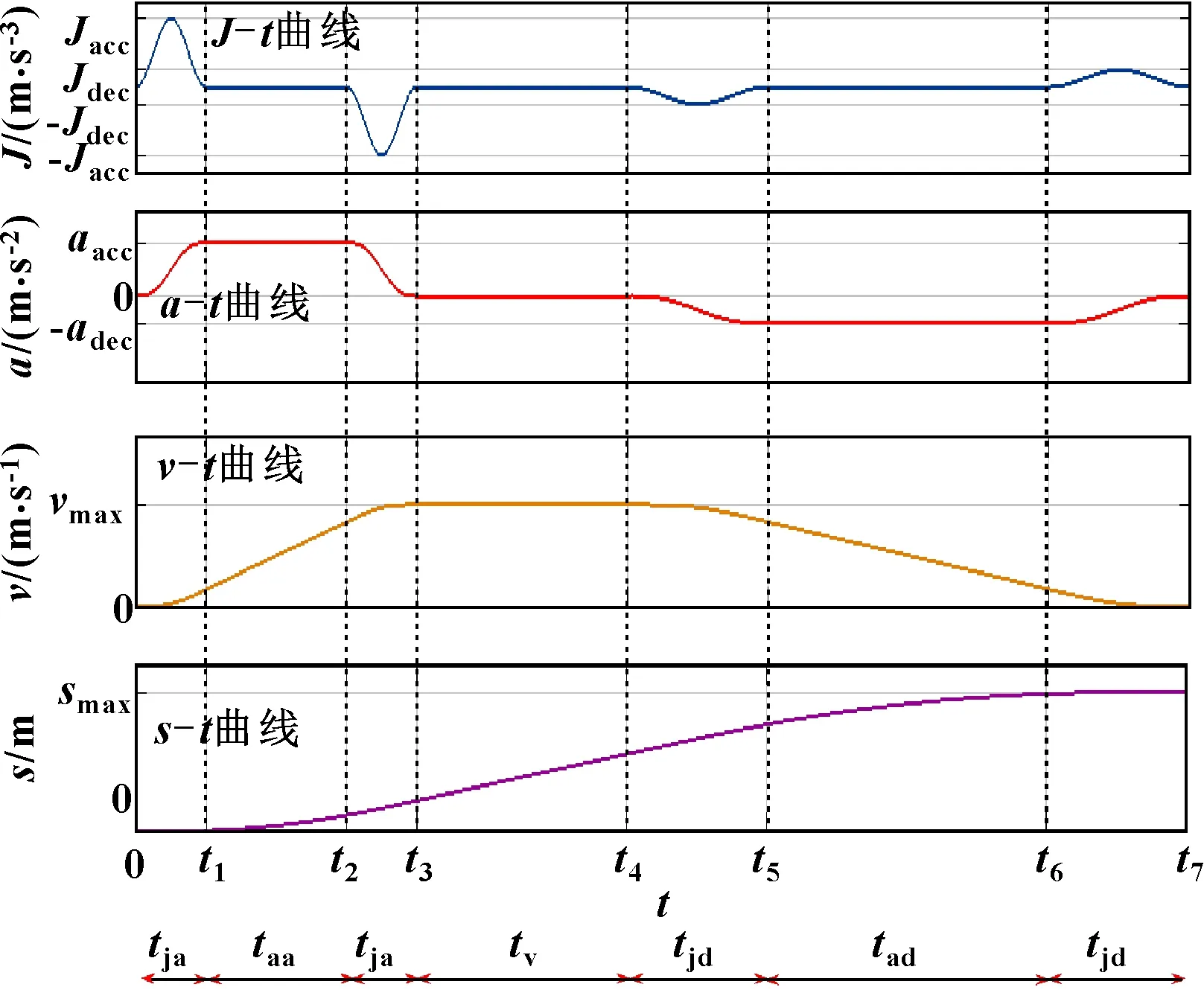
圖3 不對稱諧波AS曲線
(2)不能達到速度最大值,能達到加速度最大值和時,則有:
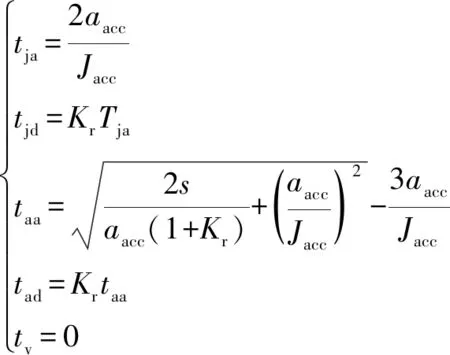
(6)
其中,能達到這種情況的最小位移值

(7)
(3)能達到速度的最大值,不能達到加速度最大值和時,則有:
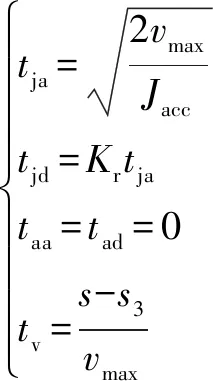
(8)
其中,能達到這種情況的最小位移值
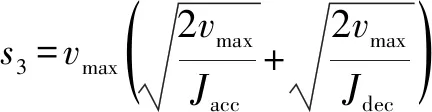
(9)
(4)不能達到速度的最大值,不能達到加速度最大值和時,則有:
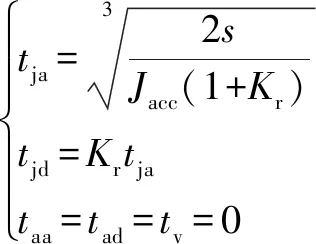
(10)
為保證所有軸同時到達目標位置,需要以最慢的軸為基礎進行時間尺度同步。=max{,,}為3個軸中的最大運動時間。除最慢的軸外其他兩軸需要重新進行運動學參數限制。同步因子利用式(11)進行計算,同時重新生成的運動學參數允許值由式(12)確定。
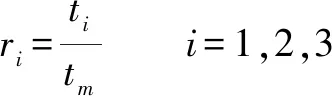
(11)

(12)
4 正弦S曲線類型選擇及參數確定
激光器的標識工作狀態應處于勻速以確保在相同時間延遲后達到下一鋼坯端面的相同位置進行打標,如果速度變化會導致每個鋼坯端面的標識位置不同,甚至不能成功打標。因此,軸2和軸3應在同一時刻開始和結束勻速段。
與諧波S曲線類似,正弦S曲線同樣由于運動距離的長短會產生4種不同情況。考慮存在勻速段的2種情況,如圖4所示。時間參數的確定與第3節諧波S曲線類似,此節側重進一步比較2種情況的勻速段在整個運動過程中的占比,以選擇勻速段占比更多的曲線類型。

圖4 存在勻速段的2種正弦S曲線


(13)
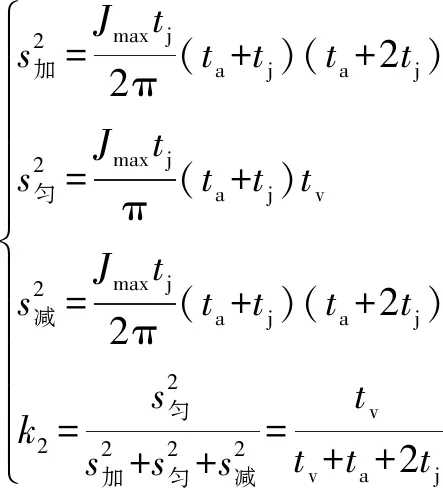
(14)
顯然,在各時間段取值相同的情況下>,即不存在勻加速度段正弦S曲線的勻速區間在整個運動過程中的占比更大,所以飛行打標過程的運動曲線選擇不存在勻加速段的正弦S曲線。激光飛行打標機構運動精度取決于直角坐標機械手軸2和軸3各自關節空間運動合成笛卡爾空間運動后的精度。它要求軸2和軸3在同一時刻開始和結束勻速段。考慮對排列在斜面上的圓鋼端面進行標識,設斜面傾角為,則軸2關節空間的位移和軸3關節空間的位移有以下關系式:

(15)
5 三次精度補償
在實際工程應用中,上述算法都需要經過離散化才能在數字控制器上實現。因此,必須將、和全部轉化為系統采樣周期的整數倍,以保證同步、提高精度。以第3節的諧波AS曲線為例進行說明,值得注意的是此補償方法對第3節的4種情況都適應。
(1)根據給定約束條件,按照第3節算法計算各時間段、和的值,轉換為采樣周期整數倍后如式(16)所示,其中[]表示不超過某個數的最大整數,為采樣周期。
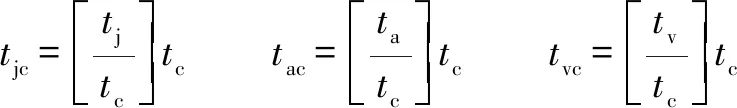
(16)
將重新計算后的、和代入算法得到補償前的位移和能達到的最大速度。與目標位移之間的差值通過增加最大速度的持續時間進行第一次精度補償。則需要增加的最大速度持續時間為
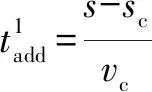
(17)
轉換為采樣周期的整數倍后:
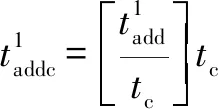
(18)
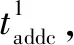
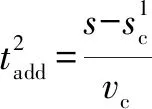
(19)
轉換為采樣周期的整數倍后:

(20)
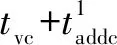
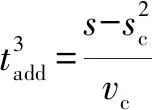
(21)
轉換為采樣周期的整數倍后:
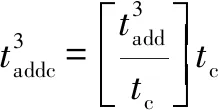
(22)
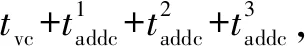
6 試驗驗證
在基于倍福PLC搭建的直角坐標機械手上分別對第3節和第4節的兩類曲線進行試驗驗證。以在平面上運動的軸2和軸3為研究對象,諧波AS曲線在兩次不同運動學參數限制條件下的運動曲線分別如圖5—圖8所示。正弦S曲線在達到最大許用運動學限制的條件下剛好能產生勻速段的極限運動情況,如圖9和圖10所示。當進一步提高運動距離或降低急動、加速度限制值時勻速段持續時間將會增加。

圖5 第一次試驗時x方向軸2的運動曲線(不能達到速度和加速度許可限制值)
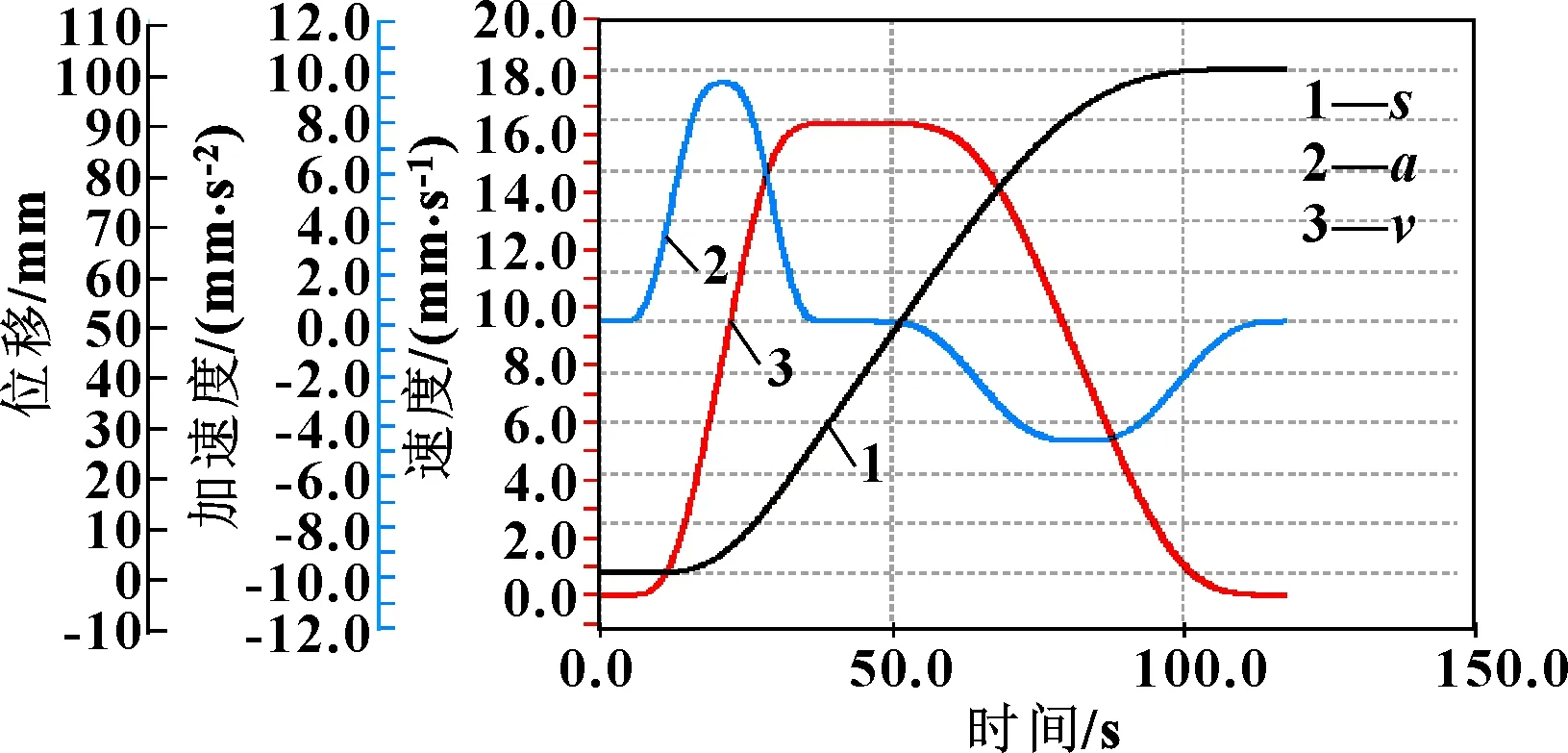
圖6 第一次試驗時y方向軸3的運動曲線(能達到速度許可限制值,不能達到加速度許可限制值)
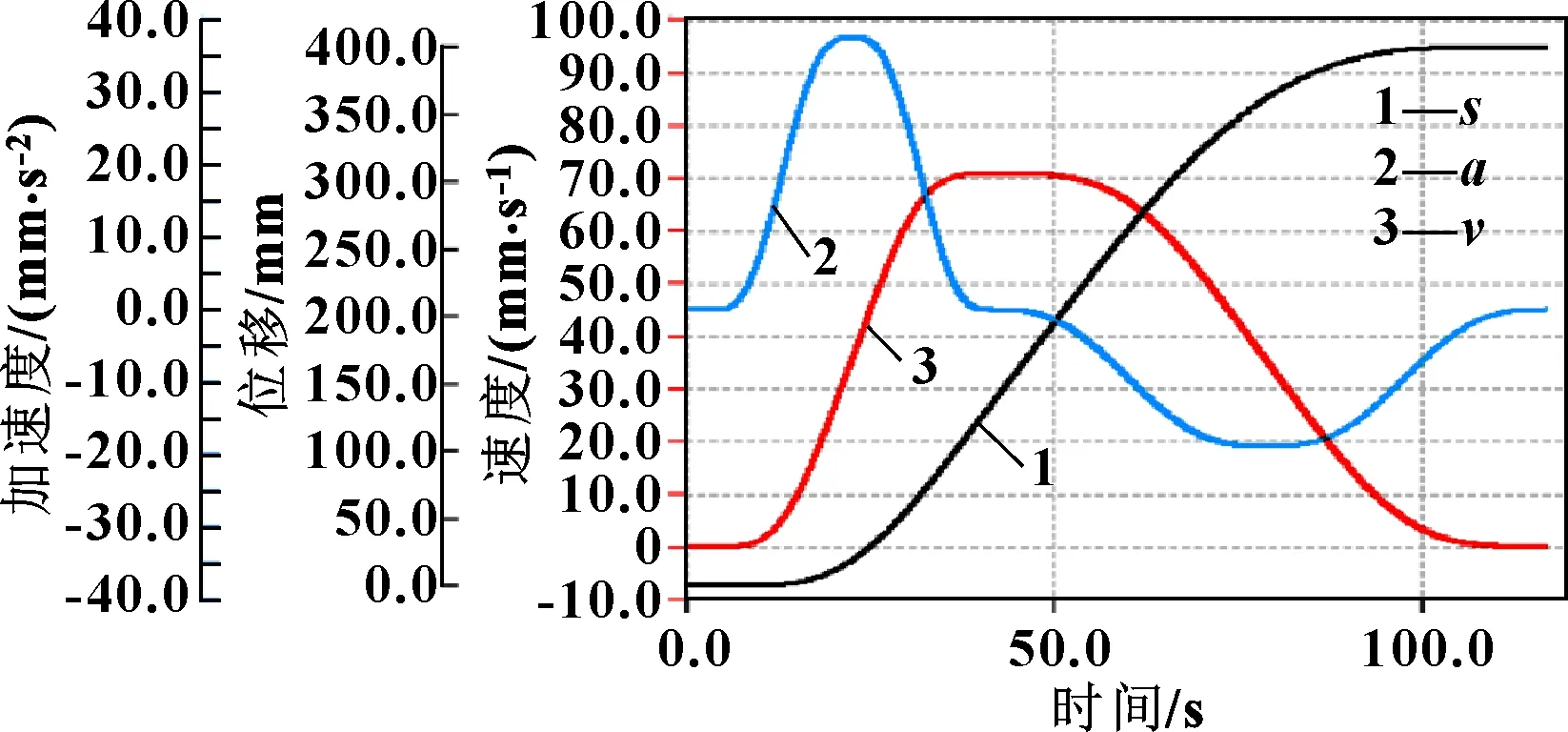
圖7 第二次試驗時x方向軸2的運動曲線(不能達到速度和加速度許可限制值)
圖8 第二次試驗時y方向軸3的運動曲線(不能達到速度和加速度許可限制值)
圖9 x方向軸2能產生勻速段的極限運動情況
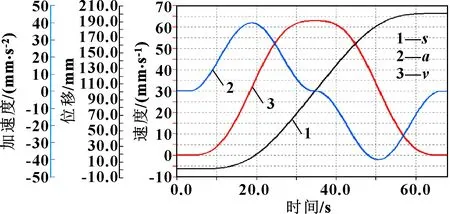
圖10 y方向軸3能產生勻速段的極限運動情況
試驗結果表明所設計的諧波AS曲線和正弦S曲線在直角坐標機械手上運行狀況良好,能滿足激光鋼坯標識過程中不同標識任務的要求。
使用不同的運動學限制進行多次試驗,前兩次試驗時軸2和軸3精度補償前后的終點位置如表1所示,多次試驗后補償前后的相對位置誤差如圖11所示。顯然,進行三次精度補償能有效縮小與目標終點位置之間的相對位置誤差,驗證了三次精度補償算法的有效性。
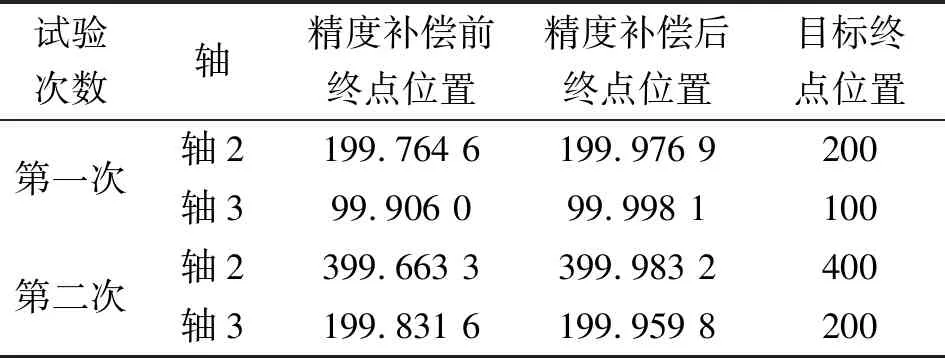
表1 諧波AS曲線三次精度補償的試驗驗證 單位:mm

圖11 軸2和軸3精度補償前后的相對位置誤差
7 結論
本文作者以運動平穩、精確為目標對激光鋼坯標識設備運行過程中的固定標識、飛行標識兩種不同的標識類型進行軌跡規劃。
(1)成功開發出了替代PLC內置梯形加減速的光滑急動S曲線運動控制功能塊。使用該功能塊時只需在對應的輸入接口處填寫運動學約束,即可得到規劃好的運動軌跡曲線。
(2)對PLC在數值轉換過程中引起的精度損失進行三次精度補償,通過增加勻速段運行時間對產生的位置誤差進行補償。
試驗結果表明:標識設備各軸運行過程平穩,經過補償后的終點位置準確。研究成果也可應用于高精度機床的平穩啟停和精確定位場合中。

