基于遺傳算法優化BP神經網絡的光伏發電功率預測

劉帥瑤，高 陽

（沈陽工程學院，遼寧沈陽 110000）

BP 神經網絡是一種由反向傳播算法控制的人工神經網絡，它適用于連續和離散自變量應用系統。它有輸入和輸出層，還有一個或多個隱藏層，每一層上的節點數是任意的，彼此獨立。它的反向傳播特性與所解決問題的性質和細節的選擇密切相關。BP 神經網絡由輸入層、輸出層和一個或多個隱藏層組成。在實踐中，更多的隱藏層模型，準確預測結果將越少，但相應地，多層結構會使系統更復雜，算法更多的冗余，所以樣品模型的訓練時間將增加，收斂速度將減少。特別是各網絡層權值的計算會非常復雜。

1 BP神經網絡結構

BP 神經網絡適用于多種自變量應用系統，主要是連續和離散自變量。它的構造有輸入和輸出層，還有一個或多個隱藏層。它的反向傳播特性與所解決問題的性質和細節的選擇密切相關。BP 神經網絡主要由輸入層、輸出層和隱藏層組成。在多數實踐中，擁有更多的隱藏層模型會使準確預測結果大幅減少，并且系統結構更復雜，所以樣品模型的總體訓練時間會上漲，隨之收斂速度急劇下降。相比之下，單隱層網絡的特點為：結構簡單、學習速度快、網絡相關權值計算準確。當有足量的隱含層節點數量時，網絡就可以使所有非線性系統的基本特征變得清晰。考慮到上述原因，本文最終選擇了精確度以及性價比高的3層結構。

2 建立BP神經網絡功率預測模型

2.1 樣本數據收集和歸一化處理

本次預測的樣本采用某光伏電站的某天發電和氣象數據。由于日落后太陽光輻射的強度幾乎為零，所以在此情境下，光伏系統的發電量也可以忽略不計。所以進行預測時忽略日落后18：30至次日6：30這段時間，將6：30至18：30設置成有效預測時間，并取預測時間間隔為1h。由于歷史數據和具體數值相關氣象因素的影響，不同日期和同一日期在不同時間下的輸出功率值有或顯著或細微的差異。隨著這些數據的輸入，不僅會使擴大搜索范圍還會使預測精度大幅降低。為了消除上述影響，需要將采集到的數據按照固定標準，對其進行歸一化處理后才可以使用。應用中一般使用premnmx 函數，通過此函數處理過后的數據會集中分布在[-1，+1]范圍內，然后再將這些數據輸入神經網絡中。premnmx 函數轉換公式如下：

其中，An是歸一化之后的數據；A表示為原始數據。

在此步驟之后，BP 祌經網絡需要在計算和學習完成后，將新的數據恢復到原來的初始數據量綱輸出，此時一般選擇用premnmx 函數來進行操作。

2.2 BP神經網絡預測模型的建立

基于BP 神經網絡算法，通過采用以下5個步驟建立光伏發電系統功率預測模型：

（1）確定網絡結構。本文選擇了由輸入層、輸出層和單隱層組成的3層BP 神經網絡模型。

（2）進行輸入層設計。根據實際情況，選擇歷史輸出功率、溫度和光照強度來作為輸入數據。選擇5個輸入層節點：在預測時間下的溫度、在預測時間前一天對應同一時刻的溫度、在預測時間下的光強度、在預測時間前一天對應同一時刻的光強度，以及在預測時間前一天對應同一時刻的歷史發電功率。

（3）進行輸出層設計。由于訓練最終目標是預測光伏系統的發電輸出功率，因此輸出層中的其中一個節點可以滿足要求。

（4）進行隱藏層設計。對于隱層節點數的設置，并沒有一個統一的標準，一般情況下符合強數定理：

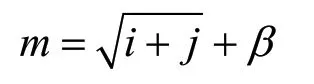
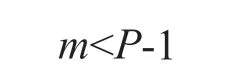
式中，m為隱含層所含有的節點數目；i為輸入層所含有節點數目；同理j對應輸出層；1≤β≤10；P為樣本數據總數。將每層所選取的節點數代入上述公式，隱層節點數選取最小值時訓練結果的誤差值最小。經計算，本文最終選擇的是目標誤差最小的4個節點來作為隱藏層中的節點數。

確定傳輸函數。確定tansig 非線性激勵函數來當隱含層的傳遞函數。選取purelin 線性函數作為輸出層的傳遞函數。

（5）計算輸出預測值的誤差。因MAPE以百分數形式出現，所以更加直觀清楚。其公式如下：

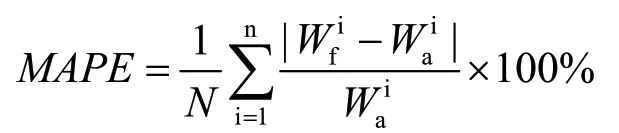
式中，N為數據集總數；Wf為功率預測值；Wa為功率實測值，i為樣本數據的序號。

3 BP神經網絡模型預測結果分析

通過MATLAB 軟件，建立本文需要使用的BP網絡功率預測模型。樣本數據來源于某一光伏電站的全天歷史發電和天氣數據，以及各類數據在預測日對應時間段的天氣預報數值。輸入歷史數據和預測日的樣本信息，經過BP 神經網絡學習和訓練后輸出預測發電功率。

表1 為樣本輸入網絡后，光伏發電預測值和實際值數據的詳細數據對比情況，誤差的絕對值在0～6 kW，平均絕對百分比誤差為MAPE=5.178%。

單片機采用AT89C52，時鐘晶體選擇AT切型的11.059 2MHz，傳感器SHT11溫濕度傳感器的DATA管腳接P1.1，SCK接P1.0。這兩個管腳要接4.7kΩ的上拉電阻。仿真軟件下不顯示SHT11的電源和地端，實際接線時，在電源和地間接入100nF的去耦濾波電容。因為數據要上傳到PC，為了實現單片機和PC間的電平轉換，實際電路要采用RS232/RS485轉換接口，但在仿真軟件元件庫中無此器件，仿真時采用RS485標準的器件MAX487的輸出端接模擬PC串口的虛擬終端。電路連接如圖4所示。

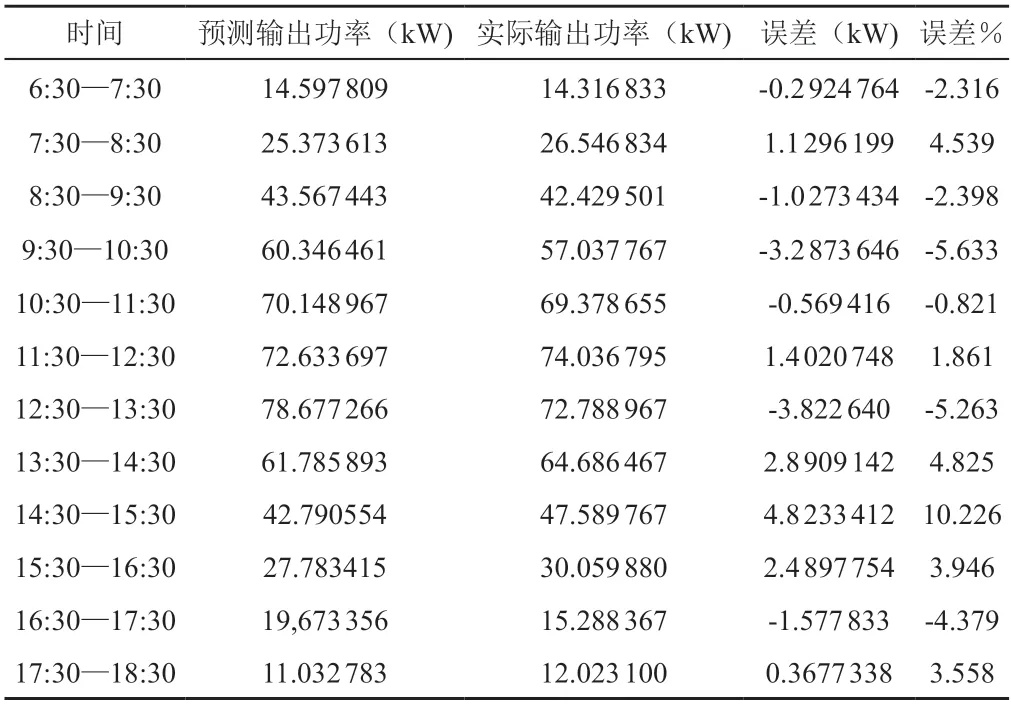
表1 實際功率和經過BP預測功率

圖1為數據樣本BP 神經網絡輸出誤差曲線的實際值和估計值之間的關系。從圖1可以看出，BP 神經網絡算法雖然可以預測更加精確的系統發電功率，但針對特殊樣本時，有些預測值與實際功率仍然存在較大偏差，有些誤差值甚至超過10%，因此還需要對此算法進行進一步改進和提高，從而達到可以提高預測輸出發電功率的精度，加快預測速度的目的。

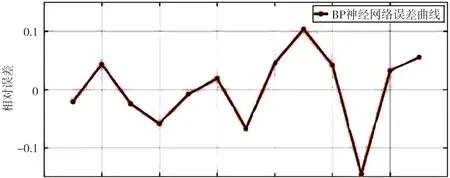
圖1 BP神經網絡發電量預測值與實際值誤差曲線

4 BP神經網絡結合優化后的遺傳算法功率預測模型

經過大量對比發現，在光伏功率預測中，BP 神經網絡的自適應能力和容錯能力非常突出，但其預測精度要依賴于大量的輸入樣本，如果數據不足，預測精度的收斂速度將極大降低，此外多重數據和擴展常數等系列參數不能同時進行計算，這也切斷了算法的一致性。因此，本文還采納了其他算法進行優化，最終選擇了遺傳算法和BP 神經網絡的交叉混合算法。

4.1 遺傳算法原理及改進

遺傳算法是一種隨機選擇優秀個體并迭代求解停產生物個體遺傳機制的搜索算法。遺傳算法自出現以來，由于其優良的特性，在許多場景中得到了廣泛的應用。遺傳算法對向量化空間中的所有解進行重復選擇、交換和變異操作，以概率方式執行優化步驟，并迭代獲得全局最優解。

遺傳算法是一種隨機選擇優秀個體并迭代求解停產生物個體遺傳機制的搜索算法。遺傳算法自出現以來，由于其優良的特性，在許多場景中得到了廣泛的應用。遺傳算法對向量化空間中的所有解進行重復選擇、交換和變異操作，以概率方式執行優化步驟，并迭代獲得全局最優解。遺傳算法的結構如下。

（1）對染色體進行編碼。將字符串類似于生物基因中的染色體，通過二進制編碼等編碼機制將樣本轉換為特定排列的數據字符串。

（2）構建適應度函數。反映在遺傳算法中，并成為判斷樣本數據字符串優劣的基礎。

（4）適當考慮其他影響因素。比如種群總數、交叉概率K。以及變異概率Km。

本文提出了一種新算法，該算法讓交叉和變異概率進行自適應計算。可以達到根據適應度值來對交叉和變異概率進行進一步優算，并且在解空間中搜索最優解的時間最大程度進行縮小。改進后的計算方法如下：

公式中f為經算法后的適應度，f'為交叉操作后的適應度值；favg為適應度的平均值；fmax為種群的最大適應度值。

4.2 BP神經網絡的優化過程

采用改進的遺傳算法優化BP 神經網絡預測模型。步驟如下。

（1）首先初始化網絡參數并歸一化訓練樣本。

（2）采用遺傳算法對網絡的權值、閾值和擴展常數進行編碼。

（3）通過BP 神經網絡的輸入層輸入樣本數據，計算其適應度函數值。

（4）通過適應度值對種群中的個體進行評價。適應值越大，個體表現越好，繁殖機會越多；反之，表現差，遺傳給后代的概率更小。

（5）生成新的種群個體并判斷適應度。如果誤差精度滿足要求，可以直接輸出網絡的模型。如果誤差范圍在需求之外，繼續下一步。

（6）判斷算法是否達到設定的迭代次數或進化代數上限。如果結果為是，則也直接輸出BP 神經網絡的最終模型。如果結果為否，則對算子進行選擇、交叉、變異等一系列操作，產生連接權值、閾值等更好的個體作為神經網絡的輸入。

5 結束語

綜上可以得知，文章將遺傳算法與BP 神經網絡相結合，形成遺傳神經網絡對風電場輸出功率進行預測，通過遺傳算法的尋優能力優化神經網絡的權值和閾值，取得了優于單一BP 神經網絡的預測結果。