基于AHP-RMM的既有建筑結構安全風險評估研究

王健 李紅民 張家瑞 閆凱 丁蕾

(1.山東建筑大學信息與電氣工程學院，山東 濟南 250101；2.山東建筑大學土木工程學院，山東 濟南 250101；3.山東省智能建筑技術重點實驗室，山東 濟南 250101)

0 引言

隨著既有建筑使用年限的增加，其安全問題成為社會關注的焦點。建筑結構一旦出現安全問題，不僅會威脅人民的生命安全，而且會造成惡劣的社會影響。因此，對既有建筑結構進行安全風險評估對于防范和化解重大建筑事故風險具有重要意義。

影響建筑結構在役狀態的因素較多，如溫度、風力等外部環境因素，因此，結構安全風險評估難度較大。高輝等[1]將模糊層次分析法應用于混凝土工程質量風險分析與評價，得出與實際相符的工程質量風險評價結果；喻巖[2]、黃慎江等[3]運用傳統9標度法確定評價指標權重，采用模糊層次分析法分別對鋼結構工業建筑和工業廠房進行了可靠性分析；陳為公等[4]通過建立考慮脆弱性的裝配式建筑安全評價體系，引入有序加權平均算子，通過模糊綜合評價對青島市三個裝配式項目進行實證分析，提出了與實際安全水平相符的評估結果；江杰等[5]采用區間層次分析法和熵權法相結合的模糊評價方式，對南寧市5層磚混結構住宅樓進行了安全評估；徐澤水[6]通過模擬評估，指出10/10～18/2標度最適宜用于精確權值計算，且評價結果較為合理；駱正清等[7]對層次分析法中的常用標度進行對比分析，得出的結論僅適用于理論證明或經驗總結，對于特定工程的實際應用有待進一步研究。通過分析相關研究文獻可知，工程結構風險貫穿于工程建設的全生命周期[8-10]。目前，雖然針對建筑施工風險評估的研究成果較多，但缺乏針對既有建筑整體結構安全風險評估的研究。

鑒于此，本文采用AHP-RMM的綜合評價方法，通過確定既有建筑結構風險源，利用AHP建立風險評估模型，并結合風險矩陣法建立各指標隸屬度函數，根據綜合評估結果確定風險等級和應對策略，以期為既有建筑結構安全風險評估提供參考。

1 建立既有建筑安全風險評估指標模型

建筑結構往往具有體量龐大、結構復雜等特點，從系統工程的角度可以視為復雜系統。以層次分析法為基礎，在參考《建筑結構可靠性設計統一標準》(GB 50068—2018)、《民用建筑可靠性鑒定標準》(GB 50292—2015)[11-12]的基礎上建立評估指標模型[3]。該評估模型由承重結構、地基基礎、結構及支撐部分和維護結構所構成的項目層及承載能力、構造連接、裂縫、變形等指標層構成，如圖1所示。

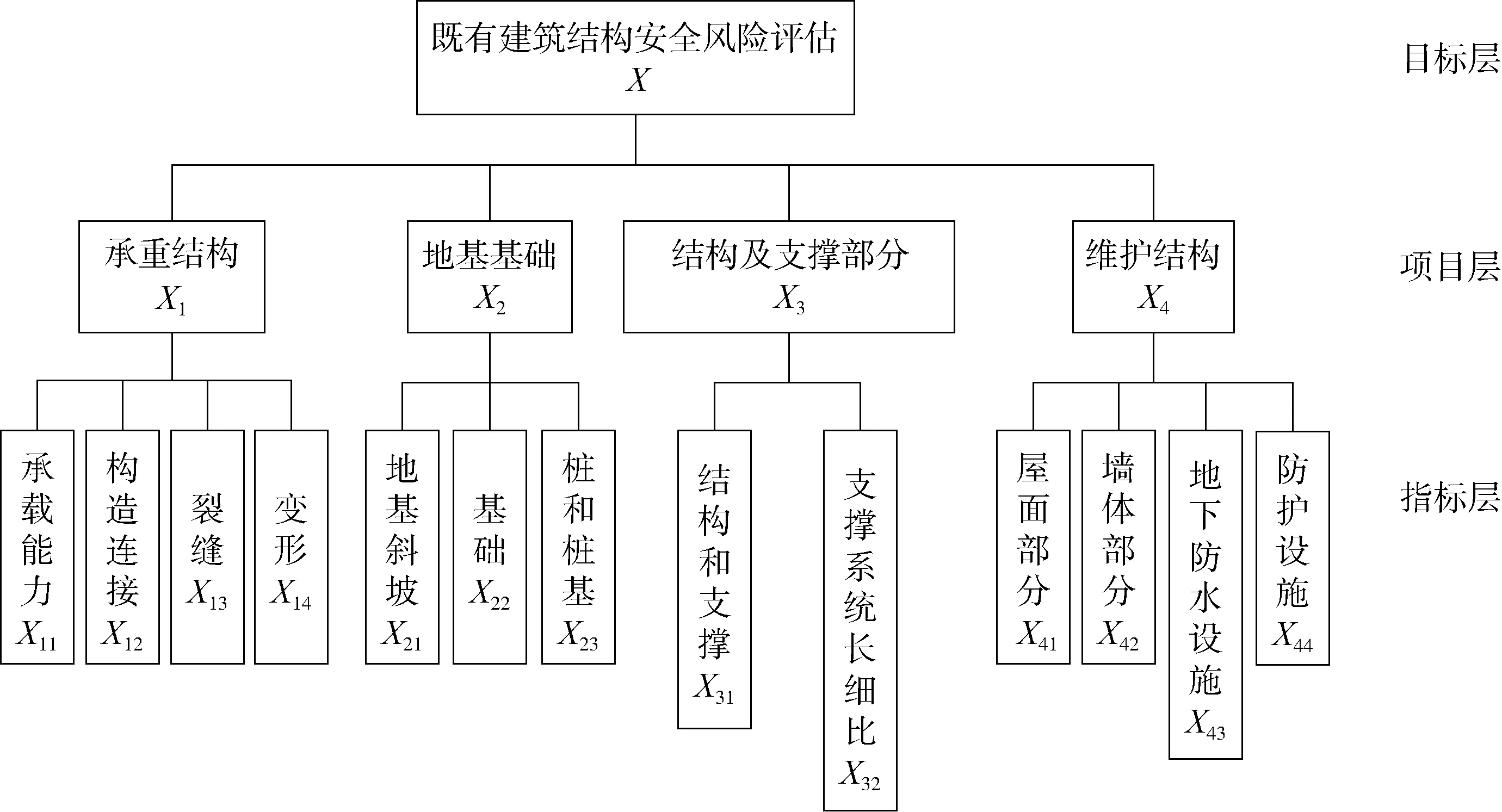
圖1 既有建筑結構安全風險評估模型

2 既有建筑結構安全風險綜合評估

2.1 確定評判因素集

既有建筑結構安全風險影響因素眾多，對其進行安全風險評估首先應建立合理的體系框架。若評判因素集中指標過多，易削弱主要指標的貢獻作用；若因素集中指標過少，則不能完全考慮建筑結構整體的安全水平。因此，確定評判因素集如下：首層為目標層，即整體建筑結構由綜合評判得出的在役安全風險水平。第二層是項目層，目標層的綜合評估結果由項目層中4個評判指標確定，項目層的評估結果由指標層確定。第三層是指標層，由4個評判指標下對應的具體指標組成，例如，承重結構項目X1可分為承載能力、構造連接、裂縫、變形4個評估指標，表示為X1=(X11,X12,X13,X14)。

2.2 確定評價集

工程實踐表明，《民用建筑可靠性鑒定標準》(GB 50292—2015)和《危險房屋鑒定標準》(JGJ 125—2016)采用的分級原則能夠有效判斷既有建筑安全水平。參照上述規范標準，將既有建筑結構安全風險水平分為4個等級，表示為U={U1,U2,U3,U4}, 分別代表低風險、一般風險、較大風險和重大危險[13]。評估結果及處理措施見表1。

表1 評估結果及處理措施

2.3 單個項目模糊評判矩陣確定

第i個指標的隸屬度cij(j=1,2,3,4)由隸屬度函數計算得出。記Ci=(ci1,ci2,ci3,ci4)為單因素評估集，表示該指標下第i個指標評估結果。綜合該指標下所有指標評估因素集，構成單層次模糊評判矩陣。以承重結構X1為例，模糊評判矩陣可表示為

(1)

式中，X1中的元素X1i隸屬于Uj等級的程度為cij(0≤cij≤1)。同理，可得到其他指標的模糊評判矩陣。

2.4 評判權重確定

標度的選取是層次分析法賦權的關鍵。為便于對比分析，本文采用三種常用標度方法構建判斷矩陣，標度值說明見表2。其中，指數標度中的λ取值在[1.1, 1.5]時符合實際結果，得出的判斷矩陣與實際結果相符合，故本文λ取值為1.2[14]。

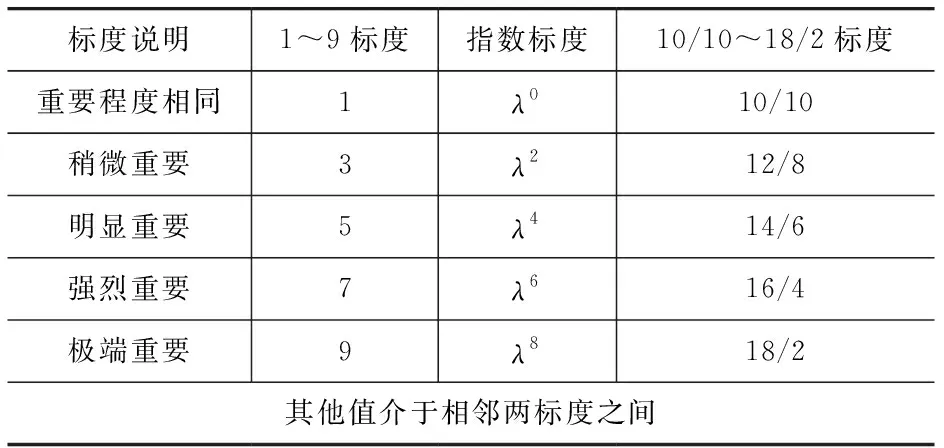
表2 標度值說明

根據比較判斷矩陣計算最大特征值和所對應的特征向量，從而確定各指標評判權重。由最大特征值得到一致性指標CI，公式如下

(2)

基于比較判斷矩陣的階數n，由RI=

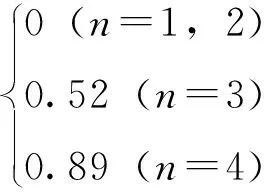
(3)

式中，若CR<0.1，則所構建的判斷矩陣符合一致性要求；若CR≥0.1，則不符合一致性要求，需要調整比較矩陣。

2.5 選取模糊算子和計算評判指標

由于評估模型具有多指標、多因素的特點，考慮到承載能力等主導變量對評估結果具有重要影響，為使評估結果更符合實際運營情況，本文的模糊算子選擇加權平均型算子M(+，·) 。評估結果B由模糊綜合評判式(4)計算得到

B=ω×C=

(4)

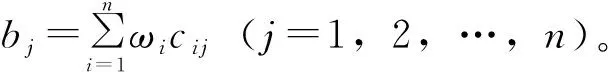
為避免實際評估中因局部構件損壞而出現風險等級隸屬度不連續的問題，引入算數加權平均進行信息集成。本文以bj作為權重，對所有評價集元素Uj進行算數加權平均，得到建筑結構安全風險的最終評估結果。公式如下

(5)

式中，ai取值為[1, 4]，分別對應評價集中各安全風險等級。

3 基于RMM的隸屬度函數構建

建立既有建筑結構安全風險評估隸屬度函數時，傳統方法需要進行嚴格的計算分析與試驗，同時，在很大程度上又依賴于已有的實際工程經驗。鑒于此，本文引入風險矩陣分析法，綜合考慮建筑結構安全風險發生的概率與致災后果的嚴重性，將風險發生概率劃分為5個等級，以估值1～5分別表示罕見、極少、偶爾、經常、頻繁。風險發生概率P見表3。

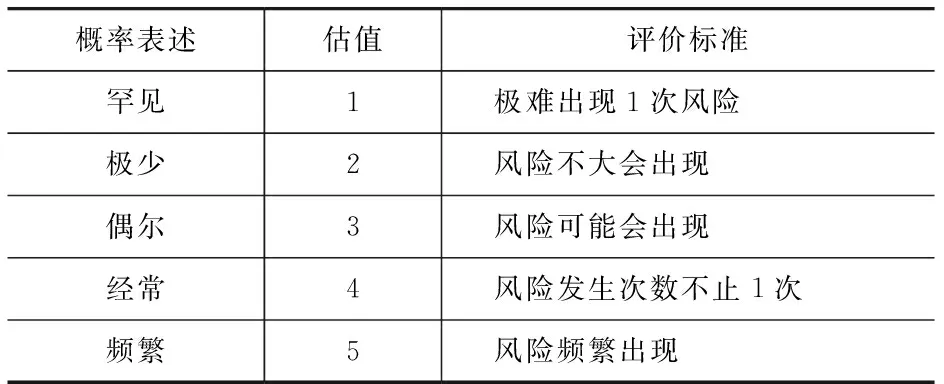
表3 風險發生概率P

將風險致災后果的嚴重性劃分為5個等級，以估值1～5分別表示輕微、中等、嚴重、重大、災難性，風險致災后果C見表4[15]。由專家打分法確定各指標風險發生概率P和致災后果C，將P與C的乘積作為風險值S。

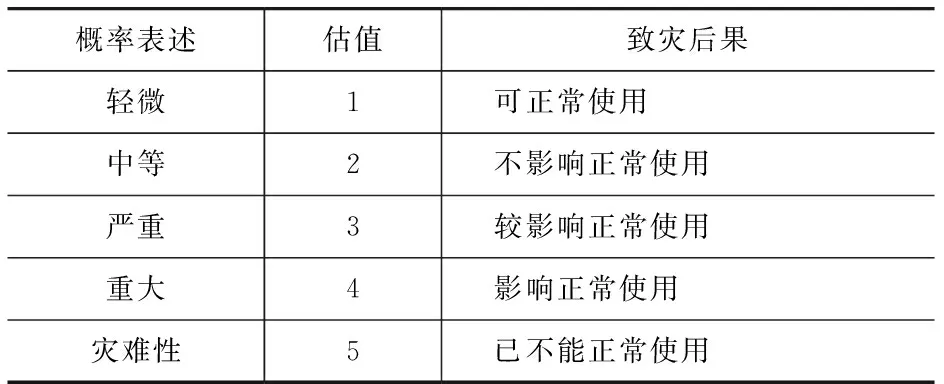
表4 風險致災后果C

結合風險發生概率和風險致災影響后果，建立風險評價矩陣，如圖2所示。本文對建筑結構安全風險的評估是在正常條件下進行的，未將不可抗力(如自然災害)考慮在內。

圖2 風險評價矩陣

在參考既有建筑結構安全相關規范和標準的基礎上，結合專家意見，確定風險邊界值與既有建筑結構風險水平之間的對應關系，見表5。

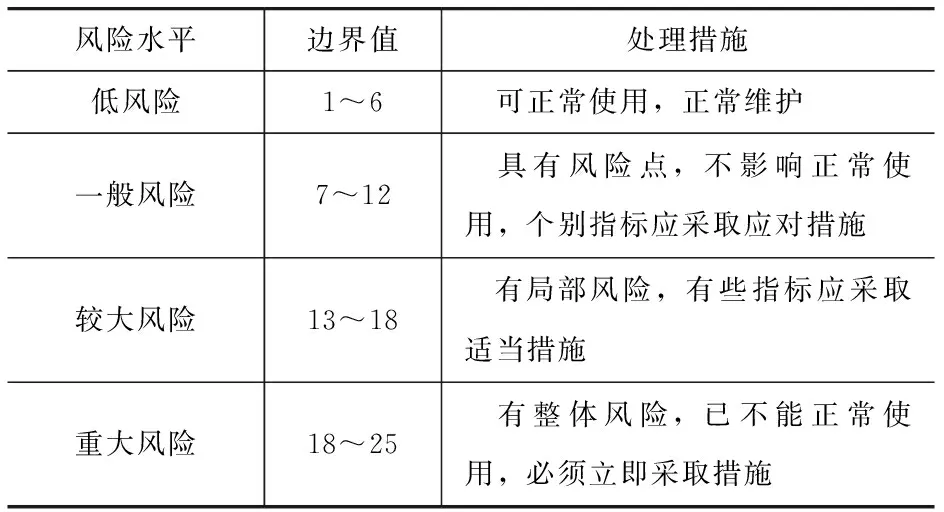
表5 風險水平與處理措施

考慮到半梯形和三角形組合分布能夠細致處理邊界值邊緣信息，同時可以保存隸屬度的邊界信息，隸屬度函數的建立采用半梯形和三角形組合而成的分布函數。定量隸屬度函數見式(6)～式(9)。則風險值S對應評價集相應等級的隸屬度函數為

(6)

(7)

(8)

(9)

4 實例分析

本文以某工業廠房建筑結構為評估對象，通過上述方法對其安全風險進行評估。各指標風險值見表6，風險值S由P與C的乘積計算得出。其中所用數據參考文獻[3]。

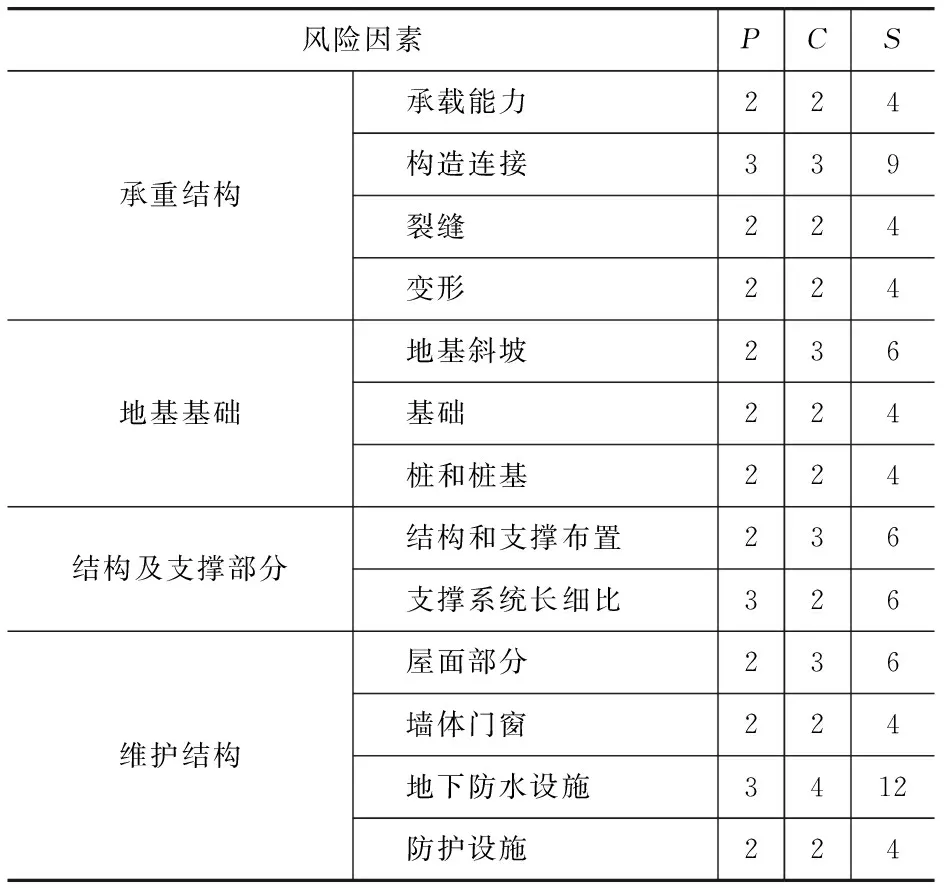
表6 各指標風險值

根據既有建筑結構安全風險評估方法，制定風險評估流程，如圖3所示。具體計算步驟如下。

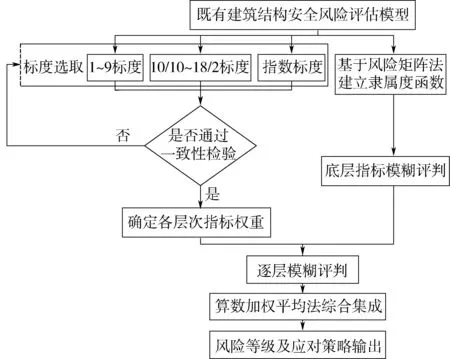
圖3 既有建筑結構安全風險評估流程

4.1 建立評判矩陣并計算指標權重

根據評估模型中各指標間的相對重要程度，參照表2構造比較判斷矩陣，由最大特征值和特征向量確定相應權重。建立指數標度下的比較判斷矩陣，見表7。同理，建立其他兩種標度評判矩陣。

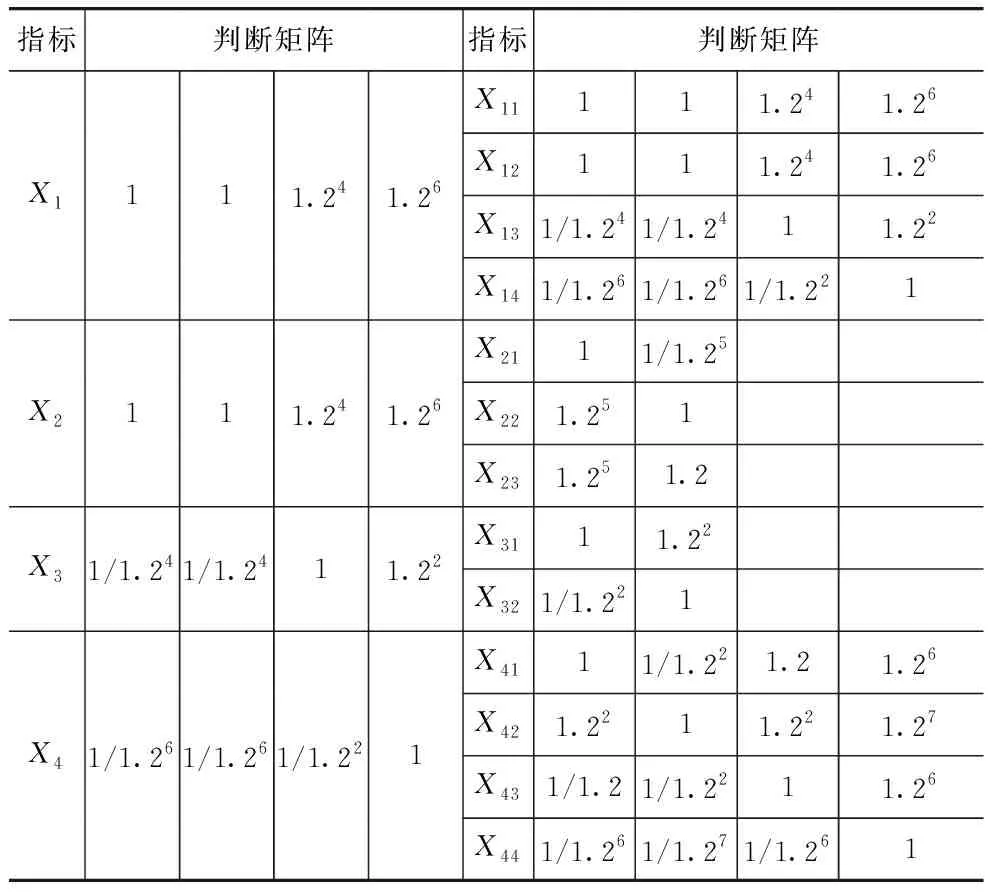
表7 基于指數標度的比較判斷矩陣

為對比分析三種標度實際應用情況，計算三種不同標度下的權重值，見表8。

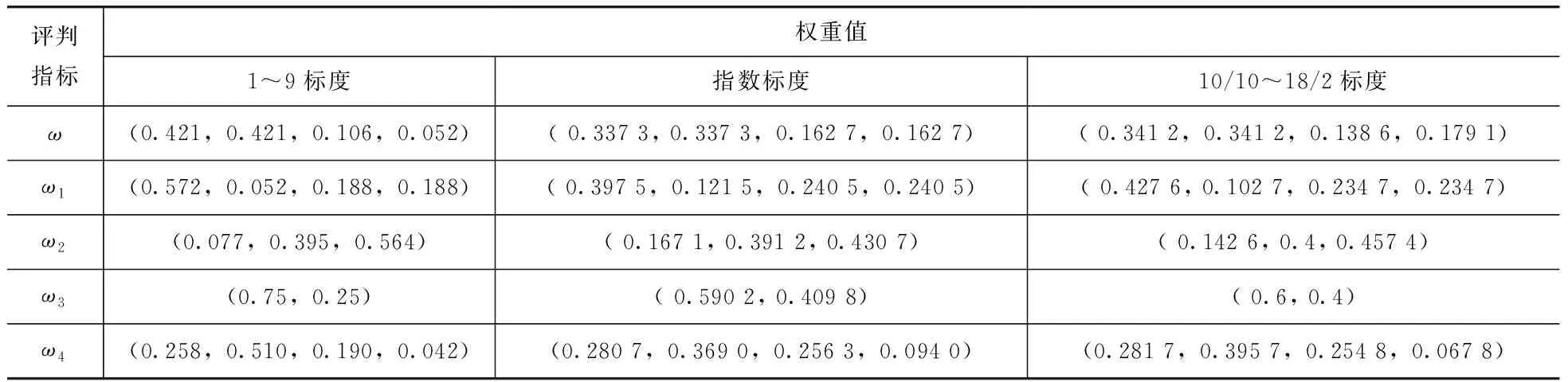
表8 三種權重值對比

4.2 計算評判矩陣

根據風險值S計算所有二級指標下各指標的隸屬度，得到相應的評判矩陣，即

4.3 確定目標層評判結果

通過權重及單因素模糊評判矩陣逐層向上計算，求出既有建筑結構安全風險綜合評判指標。三種標度下安全風險評估數值見表9。

4.4 結果分析

采用算數加權平均方式對評判矩陣B進行計算，得到評估結果U。以1～4分別表示低風險、一般風險、較大風險、嚴重風險4個等級。根據式(5)計算可知，U處于1～2，由此判斷該工業廠房風險等級處于低風險和一般風險之間，即可常使用，但有安全風險點，個別指標應采取應對措施。實例分析結果表明：

(1)從三種不同標度的評判指標計算結果可見，指數標度在實際工程中的應用較1～9和10/10～18/2兩種標度更符合實際。

(2)以評判矩陣B中元素bj為權重對評價集元素Uj進行算數加權平均后，三種標度均可得出U處于1～2的結果，由此可判斷該工業廠房結構風險處于低風險和一般風險之間，即個別指標需要維護，結構整體較安全。

(3)在同樣的工程實例下，文獻[3]得出可靠度等級為二級的結論，與本文所述方法的研究結果大致相同，說明本文提出的既有建筑結構安全風險評估方法具有一定的可行性。

5 結語

本文將層次分析法和風險矩陣法相結合，在對比三種標度下評估結果準確性的基礎上，通過模糊綜合評價方法對既有建筑結構安全風險進行評估，并建立了既有建筑結構安全風險評估流程；通過引入算數加權平均法綜合評估既有建筑結構安全風險后，在三種標度下均可得到相同評估結果；通過風險矩陣法建立隸屬度函數，簡化了常規隸屬度函數構建方法，在既有建筑物安全風險綜合評估中得到了符合實際的結果，可為既有建筑安全運維及風險管理提供參考。